人教版九年级数学下册第二十七章相似单元测试卷(Word版,附答案)
文档属性
| 名称 | 人教版九年级数学下册第二十七章相似单元测试卷(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 485.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 23:28:33 | ||
图片预览



文档简介
2021-2022学年人教版九年级数学下册
第27章《相似》单元测试
一、单选题(共30分)
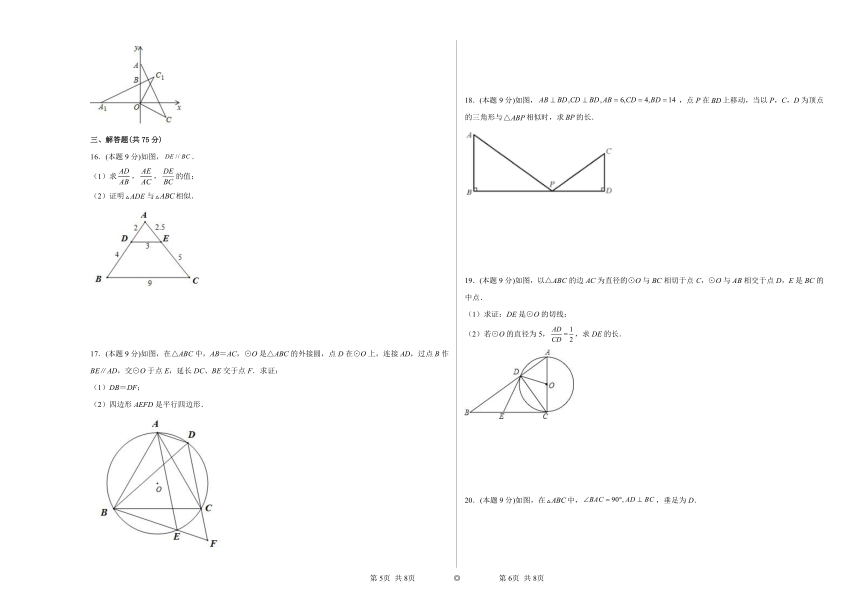
1.下列结论不正确的是( )
A.所有的矩形都相似 B.所有的正三角形都相似
C.所有的等腰直角三角形都相似 D.所有的正八边形都相似
2.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为( )
A.4:9 B.2:5 C.2:3 D.:
3.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a=b B.a=2b C.a=2b D.a=4b
4.如图,中,,且,则被分成的三部分面积之比( )
A.1∶1∶1 B.1∶2∶3 C.1∶3∶5 D.
5.如图,在△ABC中,中线BE、CD相交于点O,连结DE,下列结论中,正确的个数有( )
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
6.如图所示,已知点、、、在一条直线上,,下列( )作为条件添上,不能使得
A. B. C. D.
7.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( )
A.1.2m B.1.3m C.1.4m D.1.5m
8.如图,正方形的两边,分别在平面直角坐标系的、轴的正半轴上,正方形与正方形是以的中点为中心的位似图形,已知,若点的坐标为,则正方形与正方形的相似比是( )
A. B. C. D.
9.如图,△ABC是腰长为2的等腰直角三角形,△BCD是直角三角形,且∠D=30°,则两个三角形重叠部分(△OBC)的面积是( )
A.3﹣ B.2﹣ C.1 D.1+
10.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB、AD中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=( )
A.1.2 里 B.1.5 里 C.1.05 里 D.1.02 里
二、填空题(共15分)
11.已知:如图,,,以原点为位似中心,相似比,把在点另一侧缩小,则点的对应点的坐标为________.
12.如图,在Rt△ABC中,∠ACB=90°,BA=12cm,AD、BE是两条中线,F为其交点,那么CF=____cm.
13.如图,在四边形中,对角线与相交于点O,,在的延长线上取一点E,连接交于点F已知,则___.(用含m、n、k的代数式表示)
14.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中.面积最大的三角形的斜边长是_____.
15.△AOC在平面直角坐标系中的位置如图所示,OA=4,将△AOC绕O点,逆时针旋转90°得到△A1OC1,A1C1,交y轴于B(0,2),若△C1OB∽△C1A1O,则点C1的坐标____.
三、解答题(共75分)
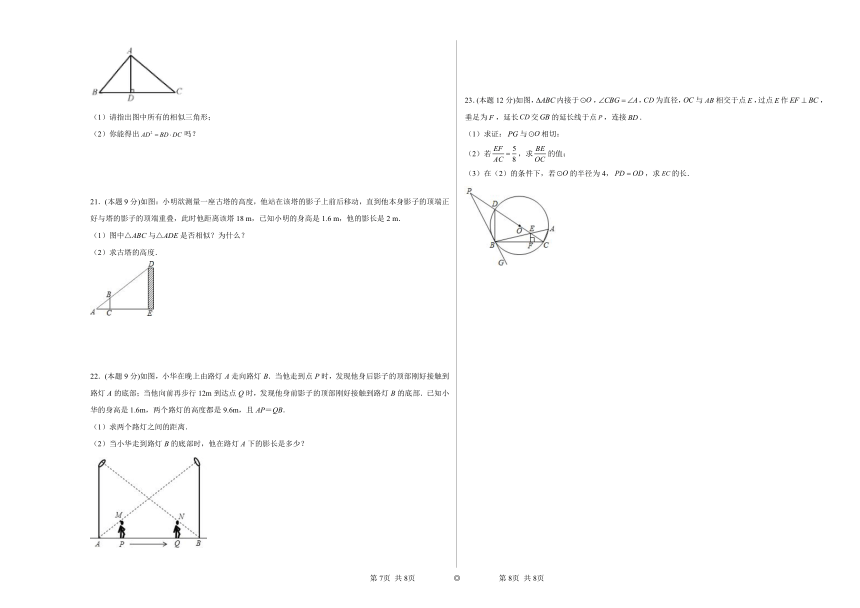
16.(本题9分)如图,.
(1)求,,的值;
(2)证明与相似.
17.(本题9分)如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,点D在⊙O上,连接AD,过点B作BE∥AD,交⊙O于点E,延长DC、BE交于点F.求证:
(1)DB=DF;
(2)四边形AEFD是平行四边形.
18.(本题9分)如图,,点P在上移动,当以P,C,D为顶点的三角形与相似时,求的长.
19.(本题9分)如图,以△ABC的边AC为直径的⊙O与BC相切于点C,⊙O与AB相交于点D,E是BC的中点.
(1)求证:DE是⊙O的切线;
(2)若⊙O的直径为5,,求DE的长.
20.(本题9分)如图,在中,,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出吗?
21.(本题9分)如图:小明欲测量一座古塔的高度,他站在该塔的影子上前后移动,直到他本身影子的顶端正好与塔的影子的顶端重叠,此时他距离该塔18 m,已知小明的身高是1.6 m,他的影长是2 m.
(1)图中△ABC与△ADE是否相似?为什么?
(2)求古塔的高度.
22.(本题9分)如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
23.(本题12分)如图,内接于,,为直径,与相交于点,过点作,垂足为,延长交的延长线于点,连接.
(1)求证:与相切:
(2)若,求的值;
(3)在(2)的条件下,若的半径为4,,求的长.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案
1.A
2.A
3.B
4.C
5.C
6.D
7.A
8.B
9.A
10.C
11.
12.4
13.
14.5
15.
16.
(1)∵,
∴,,,
即.
(2)由(1)知,,
又∵
∴,,,
∴∽(对应边成比例,对应角分别相等的两个三角形相似).
17.
解:(1)∵AD∥BE,
∴∠ADB=∠DBE,
又∵∠ADB=∠ACB,
∴∠DBE=∠ACB,
∵∠BDC=∠BAC,
∴,
∵AB=AC,
∴DB=DF;
(2)∵DB=DF, AB=AC,,
∠F=∠ACB,
∵∠AEB=∠ACB,
∴∠F=∠AEB,
∴AE∥DF,
又∵BE∥AD,
∴四边形AEFD是平行四边形.
18.
解:设DP=x,则BP=BD-x=14-x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当时,△ABP∽△CDP,即,
解得;
当时,△ABP∽△PDC,即,
整理得x2-14x+24=0,
解得x1=2,x2=12,
BP=14-2=12,BP=14-12=2,
∴当BP为8.4或2或12时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似.
19.
(1)证明:连接OD.
∵BC是⊙O的切线,AC是直径,
∴∠ACB=90°,
∵AC是直径,
∴∠ADC=90°,
∴∠CDB=90°,
又∵EB=EC
∴DE为直角△DCB斜边的中线,
∴DE=CE=BC.
∴∠DCE=∠CDE,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°,
∴∠ODE=90°
∴DE是⊙O的切线.
(2)∵ ,
∴设AD=x,CD=2x,
∵AC=5,AD2+DC2=AC2,
∴x2+(2x)2=52,
∴x=,
即AD=,CD=2,
在Rt△BDC和Rt△ADC中,∠ADC=∠BDC=90°,∠ABC=90°,
∴∠ABC+∠A=90°,∠ABC+∠BCD=90°,
∴∠A=∠BCD,
∵△ADC∽△CDB,
∴,
即 ,
∴BC=10.
∴DE=BC=5.
20.
解:(1),,;
(2)能,
,
,
,
,
,
,
,
,
;
21.
解:(1)△ABC∽△ADE.
∵BC⊥AE,DE⊥AE,
∴∠ACB=∠AED=90°.
∵∠A=∠A,
∴△ABC∽△ADE;
(2)由(1)得△ABC∽△ADE,
∴
∵AC=2m,AE=2+18=20m,BC=1.6m,
∴,
∴DE=16m,
即古塔的高度为16m.
22.
解:(1)如图1,∵PM∥BD,
∴△APM∽△ABD,
,即,
∴AP=AB,
∵QB=AP,
∴BQ=AB,
而AP+PQ+BQ=AB,
∴AB+12+AB=AB,
∴AB=18.
答:两路灯的距离为18m;
(2)如图2,他在路灯A下的影子为BN,
∵BM∥AC,
∴△NBM∽△NAC,
∴,即,解得BN=3.6.
答:当他走到路灯B时,他在路灯A下的影长是3.6m.
23.
(1)证明:如图,连接,
∵,
,
、,
,
是的直径,
∴∠DBC=90°,
,
,
,
与相切;
(2)解:过点作于点,连接,
∵OC=OA,,
∴,
,
,
∴∠EBF=∠AOM,
又,
,
,
,,
,
又,
;
(3)解:,,
,
在中,,
又,
是等边三角形,
,
,,
,
∴EC=2EF,由勾股定理FC=
设,则、,
,
,且,
,
在中,,
,
整理得
△=242-16×23=208>0
解得:,
,舍去,
,
.
答案第1页,共2页
答案第1页,共2页
第27章《相似》单元测试
一、单选题(共30分)
1.下列结论不正确的是( )
A.所有的矩形都相似 B.所有的正三角形都相似
C.所有的等腰直角三角形都相似 D.所有的正八边形都相似
2.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为( )
A.4:9 B.2:5 C.2:3 D.:
3.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a=b B.a=2b C.a=2b D.a=4b
4.如图,中,,且,则被分成的三部分面积之比( )
A.1∶1∶1 B.1∶2∶3 C.1∶3∶5 D.
5.如图,在△ABC中,中线BE、CD相交于点O,连结DE,下列结论中,正确的个数有( )
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
6.如图所示,已知点、、、在一条直线上,,下列( )作为条件添上,不能使得
A. B. C. D.
7.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( )
A.1.2m B.1.3m C.1.4m D.1.5m
8.如图,正方形的两边,分别在平面直角坐标系的、轴的正半轴上,正方形与正方形是以的中点为中心的位似图形,已知,若点的坐标为,则正方形与正方形的相似比是( )
A. B. C. D.
9.如图,△ABC是腰长为2的等腰直角三角形,△BCD是直角三角形,且∠D=30°,则两个三角形重叠部分(△OBC)的面积是( )
A.3﹣ B.2﹣ C.1 D.1+
10.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB、AD中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=( )
A.1.2 里 B.1.5 里 C.1.05 里 D.1.02 里
二、填空题(共15分)
11.已知:如图,,,以原点为位似中心,相似比,把在点另一侧缩小,则点的对应点的坐标为________.
12.如图,在Rt△ABC中,∠ACB=90°,BA=12cm,AD、BE是两条中线,F为其交点,那么CF=____cm.
13.如图,在四边形中,对角线与相交于点O,,在的延长线上取一点E,连接交于点F已知,则___.(用含m、n、k的代数式表示)
14.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中.面积最大的三角形的斜边长是_____.
15.△AOC在平面直角坐标系中的位置如图所示,OA=4,将△AOC绕O点,逆时针旋转90°得到△A1OC1,A1C1,交y轴于B(0,2),若△C1OB∽△C1A1O,则点C1的坐标____.
三、解答题(共75分)
16.(本题9分)如图,.
(1)求,,的值;
(2)证明与相似.
17.(本题9分)如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,点D在⊙O上,连接AD,过点B作BE∥AD,交⊙O于点E,延长DC、BE交于点F.求证:
(1)DB=DF;
(2)四边形AEFD是平行四边形.
18.(本题9分)如图,,点P在上移动,当以P,C,D为顶点的三角形与相似时,求的长.
19.(本题9分)如图,以△ABC的边AC为直径的⊙O与BC相切于点C,⊙O与AB相交于点D,E是BC的中点.
(1)求证:DE是⊙O的切线;
(2)若⊙O的直径为5,,求DE的长.
20.(本题9分)如图,在中,,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出吗?
21.(本题9分)如图:小明欲测量一座古塔的高度,他站在该塔的影子上前后移动,直到他本身影子的顶端正好与塔的影子的顶端重叠,此时他距离该塔18 m,已知小明的身高是1.6 m,他的影长是2 m.
(1)图中△ABC与△ADE是否相似?为什么?
(2)求古塔的高度.
22.(本题9分)如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
23.(本题12分)如图,内接于,,为直径,与相交于点,过点作,垂足为,延长交的延长线于点,连接.
(1)求证:与相切:
(2)若,求的值;
(3)在(2)的条件下,若的半径为4,,求的长.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案
1.A
2.A
3.B
4.C
5.C
6.D
7.A
8.B
9.A
10.C
11.
12.4
13.
14.5
15.
16.
(1)∵,
∴,,,
即.
(2)由(1)知,,
又∵
∴,,,
∴∽(对应边成比例,对应角分别相等的两个三角形相似).
17.
解:(1)∵AD∥BE,
∴∠ADB=∠DBE,
又∵∠ADB=∠ACB,
∴∠DBE=∠ACB,
∵∠BDC=∠BAC,
∴,
∵AB=AC,
∴DB=DF;
(2)∵DB=DF, AB=AC,,
∠F=∠ACB,
∵∠AEB=∠ACB,
∴∠F=∠AEB,
∴AE∥DF,
又∵BE∥AD,
∴四边形AEFD是平行四边形.
18.
解:设DP=x,则BP=BD-x=14-x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当时,△ABP∽△CDP,即,
解得;
当时,△ABP∽△PDC,即,
整理得x2-14x+24=0,
解得x1=2,x2=12,
BP=14-2=12,BP=14-12=2,
∴当BP为8.4或2或12时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似.
19.
(1)证明:连接OD.
∵BC是⊙O的切线,AC是直径,
∴∠ACB=90°,
∵AC是直径,
∴∠ADC=90°,
∴∠CDB=90°,
又∵EB=EC
∴DE为直角△DCB斜边的中线,
∴DE=CE=BC.
∴∠DCE=∠CDE,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°,
∴∠ODE=90°
∴DE是⊙O的切线.
(2)∵ ,
∴设AD=x,CD=2x,
∵AC=5,AD2+DC2=AC2,
∴x2+(2x)2=52,
∴x=,
即AD=,CD=2,
在Rt△BDC和Rt△ADC中,∠ADC=∠BDC=90°,∠ABC=90°,
∴∠ABC+∠A=90°,∠ABC+∠BCD=90°,
∴∠A=∠BCD,
∵△ADC∽△CDB,
∴,
即 ,
∴BC=10.
∴DE=BC=5.
20.
解:(1),,;
(2)能,
,
,
,
,
,
,
,
,
;
21.
解:(1)△ABC∽△ADE.
∵BC⊥AE,DE⊥AE,
∴∠ACB=∠AED=90°.
∵∠A=∠A,
∴△ABC∽△ADE;
(2)由(1)得△ABC∽△ADE,
∴
∵AC=2m,AE=2+18=20m,BC=1.6m,
∴,
∴DE=16m,
即古塔的高度为16m.
22.
解:(1)如图1,∵PM∥BD,
∴△APM∽△ABD,
,即,
∴AP=AB,
∵QB=AP,
∴BQ=AB,
而AP+PQ+BQ=AB,
∴AB+12+AB=AB,
∴AB=18.
答:两路灯的距离为18m;
(2)如图2,他在路灯A下的影子为BN,
∵BM∥AC,
∴△NBM∽△NAC,
∴,即,解得BN=3.6.
答:当他走到路灯B时,他在路灯A下的影长是3.6m.
23.
(1)证明:如图,连接,
∵,
,
、,
,
是的直径,
∴∠DBC=90°,
,
,
,
与相切;
(2)解:过点作于点,连接,
∵OC=OA,,
∴,
,
,
∴∠EBF=∠AOM,
又,
,
,
,,
,
又,
;
(3)解:,,
,
在中,,
又,
是等边三角形,
,
,,
,
∴EC=2EF,由勾股定理FC=
设,则、,
,
,且,
,
在中,,
,
整理得
△=242-16×23=208>0
解得:,
,舍去,
,
.
答案第1页,共2页
答案第1页,共2页
