2021-2022学年高一下学期数学人教A版(2019)必修第二册8.6.1-2直线与直线,直线与平面垂直课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册8.6.1-2直线与直线,直线与平面垂直课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 09:10:49 | ||
图片预览


文档简介
(共19张PPT)
8.6.1直线与直线垂直
8.6.2直线与平面垂直
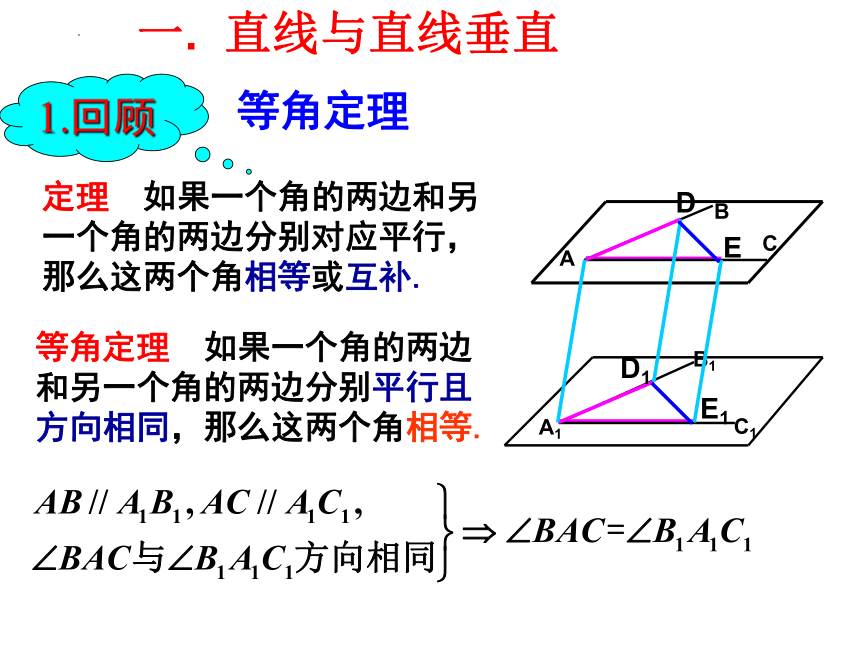
定理 如果一个角的两边和另一个角的两边分别对应平行,那么这两个角相等或互补.
等角定理 如果一个角的两边和另一个角的两边分别平行且方向相同,那么这两个角相等.
等角定理
E
E1
A
B
C
A1
B1
C1
D
D1
1.回顾
一. 直线与直线垂直
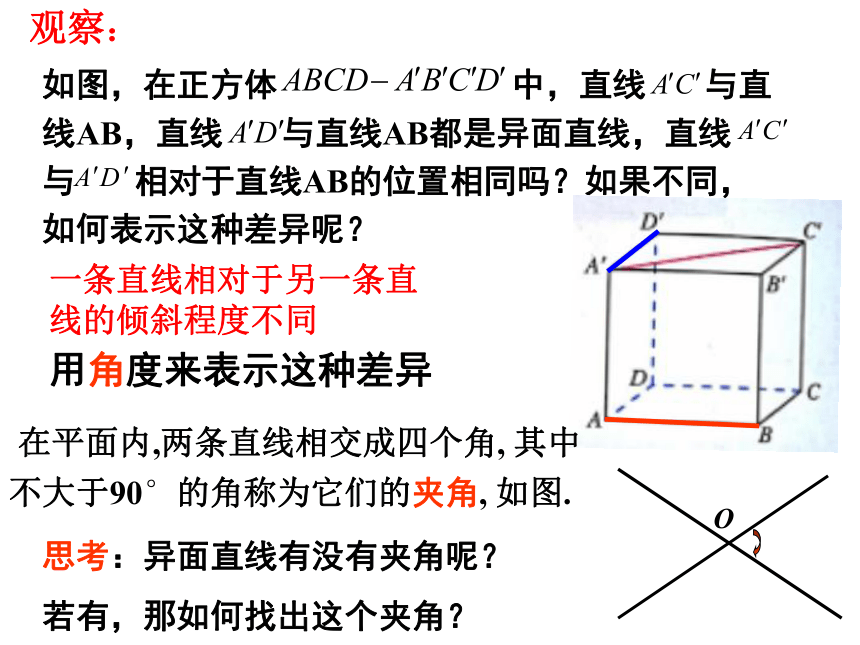
如图,在正方体 中,直线 与直线AB,直线 与直线AB都是异面直线,直线 与 相对于直线AB的位置相同吗?如果不同,如何表示这种差异呢?
观察:
一条直线相对于另一条直线的倾斜程度不同
用角度来表示这种差异
在平面内,两条直线相交成四个角, 其中不大于90°的角称为它们的夹角, 如图.
O
思考:异面直线有没有夹角呢?若有,那如何找出这个夹角?
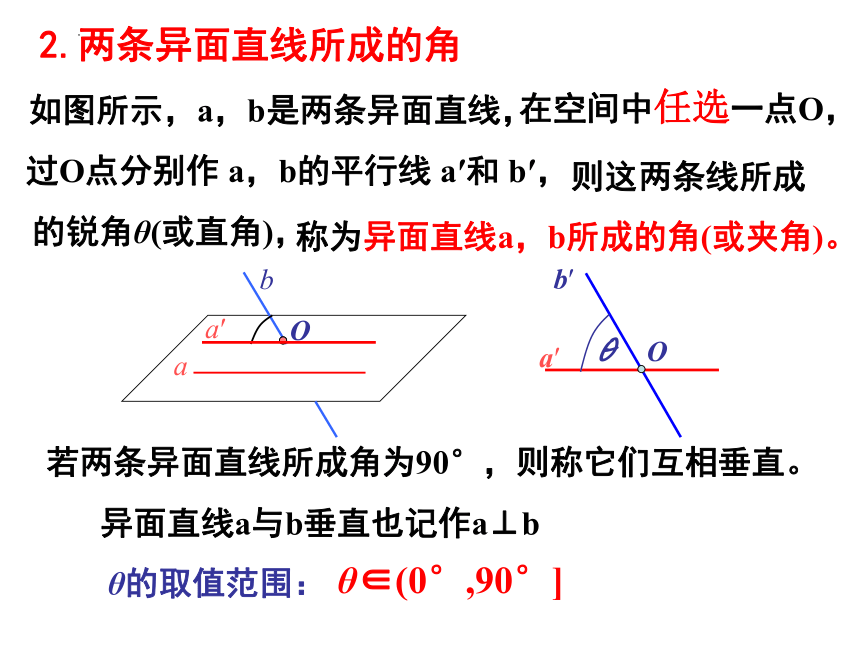
如图所示,a,b是两条异面直线,
在空间中任选一点O,
过O点分别作 a,b的平行线 a′和 b′,
a
b
P
a′
b′
O
则这两条线所成
的锐角θ(或直角),
θ
称为异面直线a,b所成的角(或夹角)。
O
a′
若两条异面直线所成角为90°,则称它们互相垂直。
异面直线a与b垂直也记作a⊥b
θ的取值范围:
θ∈(0°,90°]
2.两条异面直线所成的角
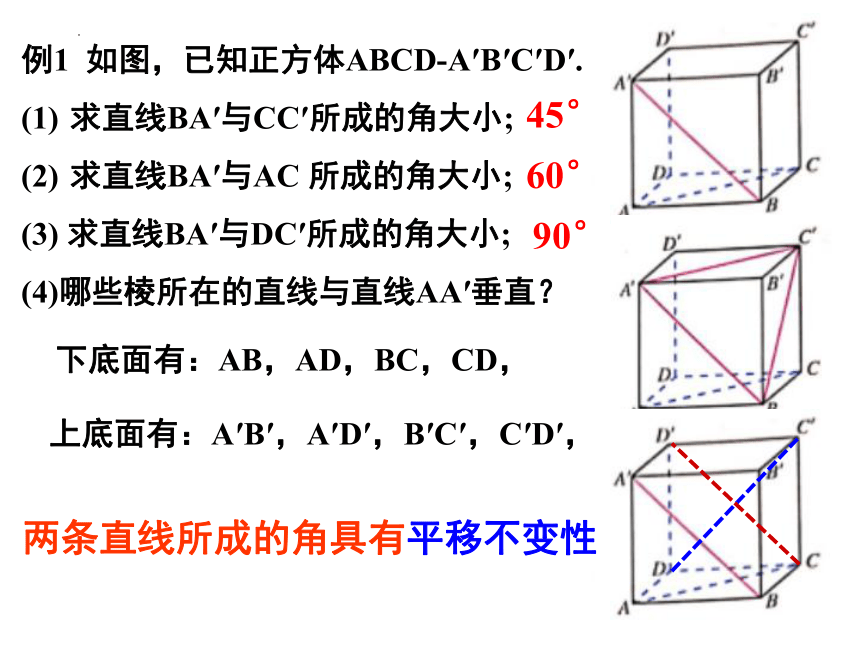
例1 如图,已知正方体ABCD-A′B′C′D′.
求直线BA′与CC′所成的角大小;
求直线BA′与AC 所成的角大小;
(3) 求直线BA′与DC′所成的角大小;
(4)哪些棱所在的直线与直线AA′垂直?
45°
60°
90°
下底面有:AB,AD,BC,CD,
上底面有:A′B′,A′D′,B′C′,C′D′,
两条直线所成的角具有平移不变性
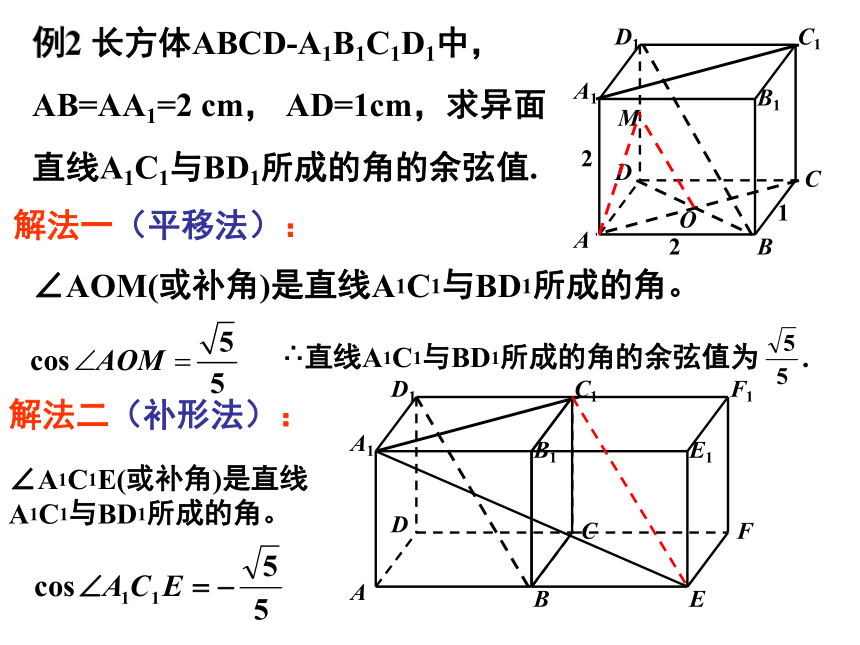
例2 长方体ABCD-A1B1C1D1中,AB=AA1=2 cm, AD=1cm,求异面直线A1C1与BD1所成的角的余弦值.
解法一(平移法):
∠AOM(或补角)是直线A1C1与BD1所成的角。
∴直线A1C1与BD1所成的角的余弦值为 .
解法二(补形法):
∠A1C1E(或补角)是直线A1C1与BD1所成的角。
A
B
C
D
A1
B1
C1
D1
O
M
A
B
C
D
A1
B1
C1
D1
E
F
E1
F1
1
2
2
生活中有很多直线与平面垂直的实例,你能举出几个吗?
旗杆与底面垂直
大桥的桥柱与水面垂直
二. 直线与平面垂直
问题1: 一条直线与一个平面垂直的意义是什么?
引入新课
在阳光下观察直立于地面的旗杆及它在地面的影子.随着时间的变化,你能发现旗杆所在直线与它的影子所在直线的位置关系吗?
B
A
C
直线AB与平面α内过B的所有直线垂直.
对于平面内不经过点B的直线呢
AB⊥B′C ′.
∴AB与平面α内的所有直线垂直.
直线与平面垂直的意义是什么
定义:如果直线l与平面α内的任意一条直线都垂直, 则称直线l与平面α互相垂直,
记作 .
如果直线 l 与平面 内的任意一条直线都垂直,我们说直线 l 与平面 互相垂直,
记作 .
平面 的垂线
直线 l 的垂面
垂足
定义
1.直线与平面垂直的意义
思考1: 如果一条直线垂直于一个平面内的无数条直线,那么这条直线是否与这个平面垂直?
B
A
C
思考2: 定义包含哪两个互逆真命题
1.如果直线 l 与平面 内的任意一条直线都垂直,则 .
2.如果 ,则直线 l 与平面 内的任意一条直线都垂直.
画法
画直线与平面垂直时,通常把直线画成表示平面的平行四边形的一边垂直,如图所示.
直线与平面的一条边垂直
问题2: 虽然定义完美无缺,无懈可击, 但难以操作, 判断直线与平面垂直能有简单易行的判定方法吗?
如图,准备一块三角形的纸片,做一个试验:
过 的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC于桌面接触).
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕 AD 与桌面所在平面 垂直.
探究
2.直线与平面垂直的判定定理
当且仅当折痕 AD 是 BC 边上的高时,AD所在直线与桌面所在平面 垂直.
探究
思考1:图中平面 内与折痕AD垂直的直线有几条 它们有什么位置关系
2.直线与平面垂直的判定定理
思考2:你能得到一个直线与平面垂直的判定定理了吗
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
2.直线与平面垂直的判定定理
简称为“若线线垂直, 则线面垂直” .
线不在多,相交则灵
判断:一条直线垂直于一个平面内的无数条直线,则该直线与此平面垂直.( )
探究
:直线与平面垂直的定义与判定定理有什么区别
(任意一条直线)
(两条相交直线)
二垂
一交
例3 如图,已知 ,求证
根据直线与平面垂直的定义知
又因为
所以
又
是两条相交直线,
所以
证明:在平面 内作
两条相交直线m,n.
因为直线 ,
典型例题
A
V
B
C
例4.如图,在正四面体V-ABC中 ,
求证:AC⊥VB
变式:求证:AB⊥VC.
N
·M
判定
线线垂直
线面垂直
定义
1.等腰三角形三线合一
2.勾股逆定理
3.构造线线角证垂直
V
A
B
C
判定
线线垂直
线面垂直
定义
1、直线与平面垂直的定义和判定
2、直线与平面所成的角
小结
1.等腰三角形三线合一
2.勾股逆定理
3.构造线线角证垂直
二垂
一交
一条直线和一个平面相交,但不和这个平面垂直,这条直线叫这个平面的斜线,斜线和平面的交点叫斜足,斜线上一点和斜足间的线段PA叫这点到这个平面的斜线段.
平面外一点到这个平面的垂线段有且只有一条,而这点到这个平面的斜线段有无数条.
3.斜线与平面所成的角
A
P
O
斜线
垂线
斜线在平面上的射影
斜足
垂足
平面的一条斜线和它在这个平面内的射影所成的夹角,叫做斜线和平面所成的角 (或斜线和平面的夹角). 简称线面角.
θ∈(0,90°)
线段PO叫这点到这个平面的垂线段.
例5、如图,在正方体ABCD-A1B1C1D1中,
求证:A1C⊥平面BC1D
A
B
C
D
A1
B1
C1
D1
点评:
第一步:找垂线
第二步:证垂直
第三步:作投影
第四步:求夹角
8.6.1直线与直线垂直
8.6.2直线与平面垂直
定理 如果一个角的两边和另一个角的两边分别对应平行,那么这两个角相等或互补.
等角定理 如果一个角的两边和另一个角的两边分别平行且方向相同,那么这两个角相等.
等角定理
E
E1
A
B
C
A1
B1
C1
D
D1
1.回顾
一. 直线与直线垂直
如图,在正方体 中,直线 与直线AB,直线 与直线AB都是异面直线,直线 与 相对于直线AB的位置相同吗?如果不同,如何表示这种差异呢?
观察:
一条直线相对于另一条直线的倾斜程度不同
用角度来表示这种差异
在平面内,两条直线相交成四个角, 其中不大于90°的角称为它们的夹角, 如图.
O
思考:异面直线有没有夹角呢?若有,那如何找出这个夹角?
如图所示,a,b是两条异面直线,
在空间中任选一点O,
过O点分别作 a,b的平行线 a′和 b′,
a
b
P
a′
b′
O
则这两条线所成
的锐角θ(或直角),
θ
称为异面直线a,b所成的角(或夹角)。
O
a′
若两条异面直线所成角为90°,则称它们互相垂直。
异面直线a与b垂直也记作a⊥b
θ的取值范围:
θ∈(0°,90°]
2.两条异面直线所成的角
例1 如图,已知正方体ABCD-A′B′C′D′.
求直线BA′与CC′所成的角大小;
求直线BA′与AC 所成的角大小;
(3) 求直线BA′与DC′所成的角大小;
(4)哪些棱所在的直线与直线AA′垂直?
45°
60°
90°
下底面有:AB,AD,BC,CD,
上底面有:A′B′,A′D′,B′C′,C′D′,
两条直线所成的角具有平移不变性
例2 长方体ABCD-A1B1C1D1中,AB=AA1=2 cm, AD=1cm,求异面直线A1C1与BD1所成的角的余弦值.
解法一(平移法):
∠AOM(或补角)是直线A1C1与BD1所成的角。
∴直线A1C1与BD1所成的角的余弦值为 .
解法二(补形法):
∠A1C1E(或补角)是直线A1C1与BD1所成的角。
A
B
C
D
A1
B1
C1
D1
O
M
A
B
C
D
A1
B1
C1
D1
E
F
E1
F1
1
2
2
生活中有很多直线与平面垂直的实例,你能举出几个吗?
旗杆与底面垂直
大桥的桥柱与水面垂直
二. 直线与平面垂直
问题1: 一条直线与一个平面垂直的意义是什么?
引入新课
在阳光下观察直立于地面的旗杆及它在地面的影子.随着时间的变化,你能发现旗杆所在直线与它的影子所在直线的位置关系吗?
B
A
C
直线AB与平面α内过B的所有直线垂直.
对于平面内不经过点B的直线呢
AB⊥B′C ′.
∴AB与平面α内的所有直线垂直.
直线与平面垂直的意义是什么
定义:如果直线l与平面α内的任意一条直线都垂直, 则称直线l与平面α互相垂直,
记作 .
如果直线 l 与平面 内的任意一条直线都垂直,我们说直线 l 与平面 互相垂直,
记作 .
平面 的垂线
直线 l 的垂面
垂足
定义
1.直线与平面垂直的意义
思考1: 如果一条直线垂直于一个平面内的无数条直线,那么这条直线是否与这个平面垂直?
B
A
C
思考2: 定义包含哪两个互逆真命题
1.如果直线 l 与平面 内的任意一条直线都垂直,则 .
2.如果 ,则直线 l 与平面 内的任意一条直线都垂直.
画法
画直线与平面垂直时,通常把直线画成表示平面的平行四边形的一边垂直,如图所示.
直线与平面的一条边垂直
问题2: 虽然定义完美无缺,无懈可击, 但难以操作, 判断直线与平面垂直能有简单易行的判定方法吗?
如图,准备一块三角形的纸片,做一个试验:
过 的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC于桌面接触).
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕 AD 与桌面所在平面 垂直.
探究
2.直线与平面垂直的判定定理
当且仅当折痕 AD 是 BC 边上的高时,AD所在直线与桌面所在平面 垂直.
探究
思考1:图中平面 内与折痕AD垂直的直线有几条 它们有什么位置关系
2.直线与平面垂直的判定定理
思考2:你能得到一个直线与平面垂直的判定定理了吗
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
2.直线与平面垂直的判定定理
简称为“若线线垂直, 则线面垂直” .
线不在多,相交则灵
判断:一条直线垂直于一个平面内的无数条直线,则该直线与此平面垂直.( )
探究
:直线与平面垂直的定义与判定定理有什么区别
(任意一条直线)
(两条相交直线)
二垂
一交
例3 如图,已知 ,求证
根据直线与平面垂直的定义知
又因为
所以
又
是两条相交直线,
所以
证明:在平面 内作
两条相交直线m,n.
因为直线 ,
典型例题
A
V
B
C
例4.如图,在正四面体V-ABC中 ,
求证:AC⊥VB
变式:求证:AB⊥VC.
N
·M
判定
线线垂直
线面垂直
定义
1.等腰三角形三线合一
2.勾股逆定理
3.构造线线角证垂直
V
A
B
C
判定
线线垂直
线面垂直
定义
1、直线与平面垂直的定义和判定
2、直线与平面所成的角
小结
1.等腰三角形三线合一
2.勾股逆定理
3.构造线线角证垂直
二垂
一交
一条直线和一个平面相交,但不和这个平面垂直,这条直线叫这个平面的斜线,斜线和平面的交点叫斜足,斜线上一点和斜足间的线段PA叫这点到这个平面的斜线段.
平面外一点到这个平面的垂线段有且只有一条,而这点到这个平面的斜线段有无数条.
3.斜线与平面所成的角
A
P
O
斜线
垂线
斜线在平面上的射影
斜足
垂足
平面的一条斜线和它在这个平面内的射影所成的夹角,叫做斜线和平面所成的角 (或斜线和平面的夹角). 简称线面角.
θ∈(0,90°)
线段PO叫这点到这个平面的垂线段.
例5、如图,在正方体ABCD-A1B1C1D1中,
求证:A1C⊥平面BC1D
A
B
C
D
A1
B1
C1
D1
点评:
第一步:找垂线
第二步:证垂直
第三步:作投影
第四步:求夹角
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
