人教版七年级数学下册9.1.2 等式性质 课件 (20张ppt)
文档属性
| 名称 | 人教版七年级数学下册9.1.2 等式性质 课件 (20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 509.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 23:48:33 | ||
图片预览








文档简介
1.理解并掌握不等式的基本性质;
2.通过实例操作,培养学生观察、分析、比较的能力,
会用不等式的基本性质解简单的不等式.(重点、难点)
学习目标
数学思想:类比思想、化归思想
等式的基本性质
(1)等式的两边都加上(或都减去)同一个数或同一个整式,等式仍然 .
(2)等式的两边都乘以(或除以)一个不为0的数,等式仍然 .
如果a=b,那么
????±????=????±????
?
相等
相等
如果a=b,那么
如果a=b(????≠0),那么
?
?????????=?????????
?
????????=??????
?
注意事项:
猜想 :不等式也具有同样的性质吗?
1、同一种运算 2、同一个数或同一个式子 3、两边除以一个不为0的数或式子
用不等号填空:
(1)5 3 ;
5+2 3+2 ;
5-2 3-2 .
.
>
>
>
<
<
<
(2)-1 3 ;
-1+2 3+2 ;
-1-3 -3-3
探究1
如果a >b,那么a±c>b±c.
不等式性质1:不等式两边 同一个数(或式子) ,不等号的方向 .
不变
加(或减)
(1)6 2;
6×5 2×5 ;
6÷2 2÷2 .
(2)-2 3 ;
-2×6 3×6 ;
-2÷2 3÷2 .
>
>
>
<
<
<
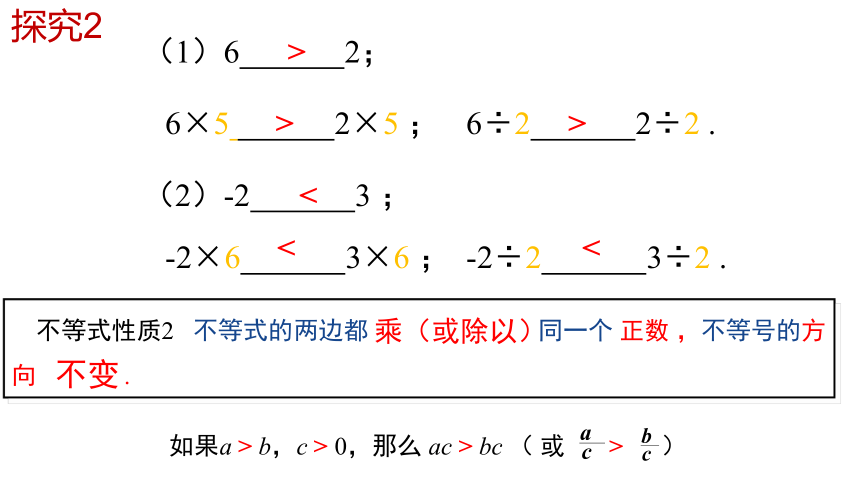
探究2
如果a > b,c > 0,那么 ac > bc ( 或 > )
不等式性质2 不等式的两边都 同一个 正数 ,不等号的方向 .
不变
乘(或除以)
(3) 6>2,
6×(-5) 2×(-5);
(4) -2<3,
(-2)×(-6) 3×(-6).
探究3
<
<
>
6÷(-2) 2÷(-2) .
-2÷(-2) 3÷(-2) .
>
即,如果a > b,c < 0,那么 ac < bc ,(或 < ).
不等式性质3: 不等式的两边都 同一个 ,不等号的方向 .
负数
改变
乘(或除以)
不等式性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即,如果a > b,c < 0,那么 ac < bc ,(或 < ).
不等式性质2 不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
如果a > b,c > 0,那么 ac > bc ( 或 > )
不等式性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a >b,那么a±c>b±c.
注意:
1、同一种运算
2、同一个数或同一个式子
3、不等式的两边都乘以或除以同一个数时,必须先认清这个数的性质符号.如果这个数是正数,那么不等号的方向不变;如果这个数是负数,那么不等号的方向改变.4、不等式的两边不能乘以0,因为乘以0后不等式变为等式.
巧记:加减不变,乘除各半,正数听话,负数造反.
例题1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a - 7____b - 7; 根据______________,两边同时 ;
(2) a÷6____b÷6; 根据______________,两边同时 ;
(3) 0.1a____0.1b; 根据______________,两边同时 ;
(4) -4a____-4b; 根据______________,两边同时 ;
(5) 2a+3____2b+3; 根据______________,两边同时 ;
(6)(m2+1)a____ (m2+1)b(m为常数) 根据______________,两边同时 ;
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
三、典例解析
减7
除以6
乘以0.1
乘以-4
乘以2再加上3
乘以(m2+1)
?判断下列各题的推导是否正确?为什么?
(1)因为7.5>5.7,所以-7.5<-5.7;( )
(2)因为a+8>4,所以a>-4; ( )
(3)因为4a>4b,所以a>b; ( )
(4)因为-1>-2,所以-a-1>-a-2; ( )
(5)因为3>2,所以3a>2a. ( )
(6)如果a>b,那么ac>bc. ( )
(7)如果a>b,那么ac2>bc2. ( )
(8)如果ac2>bc2,那么a>b. ( )
小组讨论
√
√
√
√
×
×
×
√
例题2:利用不等式的性质解下列不等式:
(1) x-7>26;(2) 3x<2x+1;(3) >50;(4) -4x>3.
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1~3
思路:
解 (1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得 x-7+7﹥26+7,即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1) x-7>26;
(2)为了使不等式3x<2x+1中不等号的一边变为x,根据_____________,不等式两边都减去____,不等号的方向_____,得 .
3x-2x﹤2x+1-2x ,即 x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
不等式性质1
2x
不变
(2) 3x<2x+1;
(3)为了使不等式 ﹥50中不等号的一边变为x,根据不等式的性质2,不等式的两边都除以 ,不等号的方向不变,得
x﹥75.
这个不等式的解集在数轴上的表示如图所示:
0
75
(3) >50;
(4)为了使不等式-4x﹥3中的不等号的一边变为x,根据______________,不等式两边都除以____,不等号的方向______,得
x﹤- .
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的性质3
-4
改变
(4) -4x>3.
例题总结:1、化为x>a或x﹤a的形式
2、选择性质,去常数还是去系数
巩固练习
练习2、根据不等式的性质,解下列不等式,并在数轴上表示其解集:
(1)x+2≤3; (2) 2x>8;
(3)-2x>4; (4)2x+1>5.
3. (2019广西桂林)如果a>b,c<0,那么下列不等式成立的是( ).
A.a+c>b B.a+c>b-c
C.ac-1>bc-1 D.a(c-1)<b(c-1)
能力提升
4、如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.
D
a<-1
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
通过本课时的学习,需要我们掌握:
课堂小结
注意:不等式的两边不能乘以0,因为乘以0后不等式变为等式.
巧记:加减不变,乘除各半,正数听话,负数造反.
作业
1、达标作业:
1.如果a>b,用用“>”或“<”填空:
a+2__b+2; a-3__b-3; a/2__b/2;-8.5a+2__-8.5b+2;
2.若a>0,b<0,c<0 则(a-b)c___0;
若a0 则ac+c___bc+c.
3. ① a>0 x>y则:ax____ay;② a<0 x4如果a<b<0那么一定成立的不等式是( )
(1)x-1≤3; (2)15x>-2;(3)-12x<8; (4) 6<2x-12. (5)12x+1<-1;
5. 利用不等式的性质解下列不等式,并在数轴上表示其解集.
(1)x-1≤3;(2)x>-2;(3)-x<8;(4) 6x<2x-12.(5)x+1<-1;
?
1、必做作业:完成导学案达标作业2、选做作业:完成练习册68页第19、20、21、22、23题
2.通过实例操作,培养学生观察、分析、比较的能力,
会用不等式的基本性质解简单的不等式.(重点、难点)
学习目标
数学思想:类比思想、化归思想
等式的基本性质
(1)等式的两边都加上(或都减去)同一个数或同一个整式,等式仍然 .
(2)等式的两边都乘以(或除以)一个不为0的数,等式仍然 .
如果a=b,那么
????±????=????±????
?
相等
相等
如果a=b,那么
如果a=b(????≠0),那么
?
?????????=?????????
?
????????=??????
?
注意事项:
猜想 :不等式也具有同样的性质吗?
1、同一种运算 2、同一个数或同一个式子 3、两边除以一个不为0的数或式子
用不等号填空:
(1)5 3 ;
5+2 3+2 ;
5-2 3-2 .
.
>
>
>
<
<
<
(2)-1 3 ;
-1+2 3+2 ;
-1-3 -3-3
探究1
如果a >b,那么a±c>b±c.
不等式性质1:不等式两边 同一个数(或式子) ,不等号的方向 .
不变
加(或减)
(1)6 2;
6×5 2×5 ;
6÷2 2÷2 .
(2)-2 3 ;
-2×6 3×6 ;
-2÷2 3÷2 .
>
>
>
<
<
<
探究2
如果a > b,c > 0,那么 ac > bc ( 或 > )
不等式性质2 不等式的两边都 同一个 正数 ,不等号的方向 .
不变
乘(或除以)
(3) 6>2,
6×(-5) 2×(-5);
(4) -2<3,
(-2)×(-6) 3×(-6).
探究3
<
<
>
6÷(-2) 2÷(-2) .
-2÷(-2) 3÷(-2) .
>
即,如果a > b,c < 0,那么 ac < bc ,(或 < ).
不等式性质3: 不等式的两边都 同一个 ,不等号的方向 .
负数
改变
乘(或除以)
不等式性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即,如果a > b,c < 0,那么 ac < bc ,(或 < ).
不等式性质2 不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
如果a > b,c > 0,那么 ac > bc ( 或 > )
不等式性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a >b,那么a±c>b±c.
注意:
1、同一种运算
2、同一个数或同一个式子
3、不等式的两边都乘以或除以同一个数时,必须先认清这个数的性质符号.如果这个数是正数,那么不等号的方向不变;如果这个数是负数,那么不等号的方向改变.4、不等式的两边不能乘以0,因为乘以0后不等式变为等式.
巧记:加减不变,乘除各半,正数听话,负数造反.
例题1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a - 7____b - 7; 根据______________,两边同时 ;
(2) a÷6____b÷6; 根据______________,两边同时 ;
(3) 0.1a____0.1b; 根据______________,两边同时 ;
(4) -4a____-4b; 根据______________,两边同时 ;
(5) 2a+3____2b+3; 根据______________,两边同时 ;
(6)(m2+1)a____ (m2+1)b(m为常数) 根据______________,两边同时 ;
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
三、典例解析
减7
除以6
乘以0.1
乘以-4
乘以2再加上3
乘以(m2+1)
?判断下列各题的推导是否正确?为什么?
(1)因为7.5>5.7,所以-7.5<-5.7;( )
(2)因为a+8>4,所以a>-4; ( )
(3)因为4a>4b,所以a>b; ( )
(4)因为-1>-2,所以-a-1>-a-2; ( )
(5)因为3>2,所以3a>2a. ( )
(6)如果a>b,那么ac>bc. ( )
(7)如果a>b,那么ac2>bc2. ( )
(8)如果ac2>bc2,那么a>b. ( )
小组讨论
√
√
√
√
×
×
×
√
例题2:利用不等式的性质解下列不等式:
(1) x-7>26;(2) 3x<2x+1;(3) >50;(4) -4x>3.
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1~3
思路:
解 (1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得 x-7+7﹥26+7,即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1) x-7>26;
(2)为了使不等式3x<2x+1中不等号的一边变为x,根据_____________,不等式两边都减去____,不等号的方向_____,得 .
3x-2x﹤2x+1-2x ,即 x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
不等式性质1
2x
不变
(2) 3x<2x+1;
(3)为了使不等式 ﹥50中不等号的一边变为x,根据不等式的性质2,不等式的两边都除以 ,不等号的方向不变,得
x﹥75.
这个不等式的解集在数轴上的表示如图所示:
0
75
(3) >50;
(4)为了使不等式-4x﹥3中的不等号的一边变为x,根据______________,不等式两边都除以____,不等号的方向______,得
x﹤- .
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的性质3
-4
改变
(4) -4x>3.
例题总结:1、化为x>a或x﹤a的形式
2、选择性质,去常数还是去系数
巩固练习
练习2、根据不等式的性质,解下列不等式,并在数轴上表示其解集:
(1)x+2≤3; (2) 2x>8;
(3)-2x>4; (4)2x+1>5.
3. (2019广西桂林)如果a>b,c<0,那么下列不等式成立的是( ).
A.a+c>b B.a+c>b-c
C.ac-1>bc-1 D.a(c-1)<b(c-1)
能力提升
4、如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.
D
a<-1
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
通过本课时的学习,需要我们掌握:
课堂小结
注意:不等式的两边不能乘以0,因为乘以0后不等式变为等式.
巧记:加减不变,乘除各半,正数听话,负数造反.
作业
1、达标作业:
1.如果a>b,用用“>”或“<”填空:
a+2__b+2; a-3__b-3; a/2__b/2;-8.5a+2__-8.5b+2;
2.若a>0,b<0,c<0 则(a-b)c___0;
若a
3. ① a>0 x>y则:ax____ay;② a<0 x
(1)x-1≤3; (2)15x>-2;(3)-12x<8; (4) 6<2x-12. (5)12x+1<-1;
5. 利用不等式的性质解下列不等式,并在数轴上表示其解集.
(1)x-1≤3;(2)x>-2;(3)-x<8;(4) 6x<2x-12.(5)x+1<-1;
?
1、必做作业:完成导学案达标作业2、选做作业:完成练习册68页第19、20、21、22、23题
