2.2简谐运动的描述 同步练习(Word版含解析)
文档属性
| 名称 | 2.2简谐运动的描述 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览



文档简介
人教版(2019)选择性必修一 2.2 简谐运动的描述
一、单选题
1.如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间距离是20 cm,从A到B运动时间是2 s,则( )
A.从O→B→O振子做了一次全振动
B.从B开始经过6 s,振子通过的路程是60 cm
C.振动周期为2 s,振幅是10 cm
D.从O开始经过3 s,振子处在平衡位置
2.有一个在y方向上做简谐运动的物体,其振动图像如图所示。下列选项中v、F、a分别表示物体的速度、受到的回复力和加速度,关于图甲、乙、丙、丁的判断正确的是( )
A.甲可作为该物体的F—t图像 B.乙可作为该物体的v—t图像
C.丙可作为该物体的v—t图像 D.丁可作为该物体的a—t图像
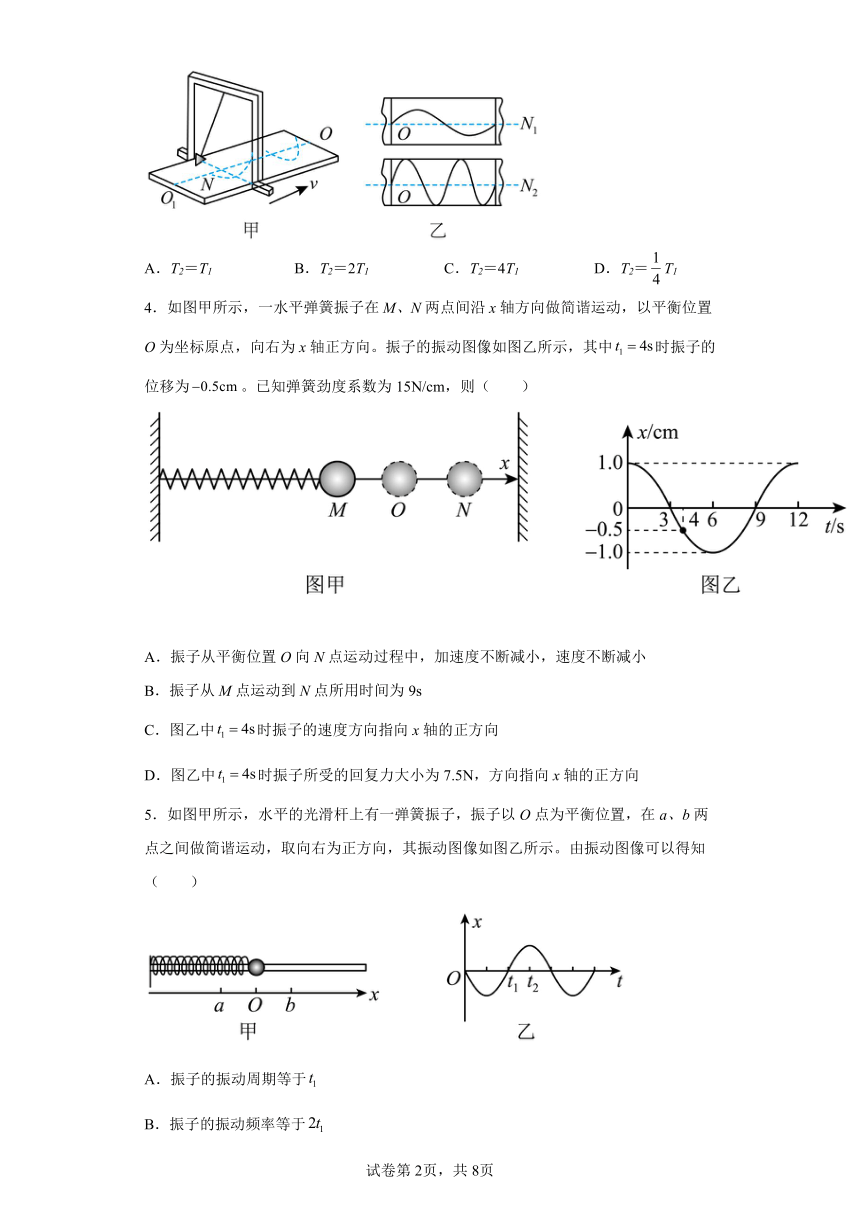
3.如图甲所示是演示简谐运动图像的装置,当漏斗下面的薄木板N被匀速地拉出时,振动着的漏斗中漏出的沙在板上形成的曲线显示出摆的位移随时间变化的关系。板上的直线OO1代表时间轴,图乙中是两个摆中的沙在各自板上形成的曲线,若板N1和板N2拉动的速度v1和v2的关系为v2=2v1,则板N1、N2上曲线所代表的周期T1和T2的关系为( )
A.T2=T1 B.T2=2T1 C.T2=4T1 D.T2=T1
4.如图甲所示,一水平弹簧振子在M、N两点间沿x轴方向做简谐运动,以平衡位置O为坐标原点,向右为x轴正方向。振子的振动图像如图乙所示,其中时振子的位移为。已知弹簧劲度系数为15N/cm,则( )
A.振子从平衡位置O向N点运动过程中,加速度不断减小,速度不断减小
B.振子从M点运动到N点所用时间为9s
C.图乙中时振子的速度方向指向x轴的正方向
D.图乙中时振子所受的回复力大小为7.5N,方向指向x轴的正方向
5.如图甲所示,水平的光滑杆上有一弹簧振子,振子以O点为平衡位置,在a、b两点之间做简谐运动,取向右为正方向,其振动图像如图乙所示。由振动图像可以得知( )
A.振子的振动周期等于
B.振子的振动频率等于
C.在时刻,振子的位置在a点
D.在时刻,振子向右经过O点
6.如图所示,小球在竖直平面内以半径为、角速度为沿逆时针方向做匀速圆周运动,用竖直向下的平行光照射小球,观察到其影子在水平面上做简谐运动。取圆心投影点为原点,水平向右为正方向建立坐标系,从小球某次经最高点的时刻开始计时,关于影子的说法正确是( )
A.振幅为
B.振动过程中的最大速度为
C.振动周期为
D.位移表达式为
7.一质点做简谐运动的图像如图所示,则在0~0.4s内,下列结论中正确的是( )
A.质点速度最大而加速度为零的时刻分别是0、0.3s
B.质点速度为零而加速度为负方向最大值的时刻分别是0、0.3s
C.质点所受的回复力方向由正变负的时刻是0.3s
D.振动系统势能最大而加速度为正方向最大值的时刻是0.3s
8.如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间距离是30cm,从A到B运动时间是4s,则( )
A.从振了做了一次全振动
B.振动周期为4s,振幅是15cm
C.从B开始经过6s,振子通过的路程是45cm
D.从O开始经过6s,振子处在平衡位置
9.某质点的振动图像如图所示,该质点的速度方向始终沿x轴正方向的时间段为( )
A.t=0~2s B.t=1~3s C.t=2~4s D.t=3~5s
10.弹簧振子做简谐运动时,从振子经过某一位置A开始计时,则( )
A.当振子再次经过A时,已通过的路程一定是4倍振幅
B.当振子再次经过A时,经过的时间一定是半周期
C.当振子的加速度再次与零时刻的加速度相同时,一定又到达位置A
D.一定还有另外一个位置跟位置A有相同的位移
11.一个做简谐运动的物体,频率为25Hz,那么它从一侧最大位移的中点,振动到另一侧最大位移的中点所用的时间( )
A.等于0.01s B.一定小于0.01s C.可能大于0.01s D.无法确定
12.如图所示为某弹簧振子在0~5 s内的振动图像,由图可知,下列说法中正确的是( )
A.振动周期为5 s,振幅为8 cm
B.第2 s末振子的速度为负
C.从第1 s末到第2 s末振子在做加速运动
D.第3 s末振子的速度为正向的最大值
13.如图所示的弹簧振子水平放置,忽略各种阻力时,它将在COB之间来回往复的做简谐振动,其中O点为平衡位置,简谐振动的振幅为A,弹簧的劲度系数为k,原长为L,弹簧振子的周期为T,小球质量为m,且规定向右为位移的正方向。请由此判断下列说法正确的是( )
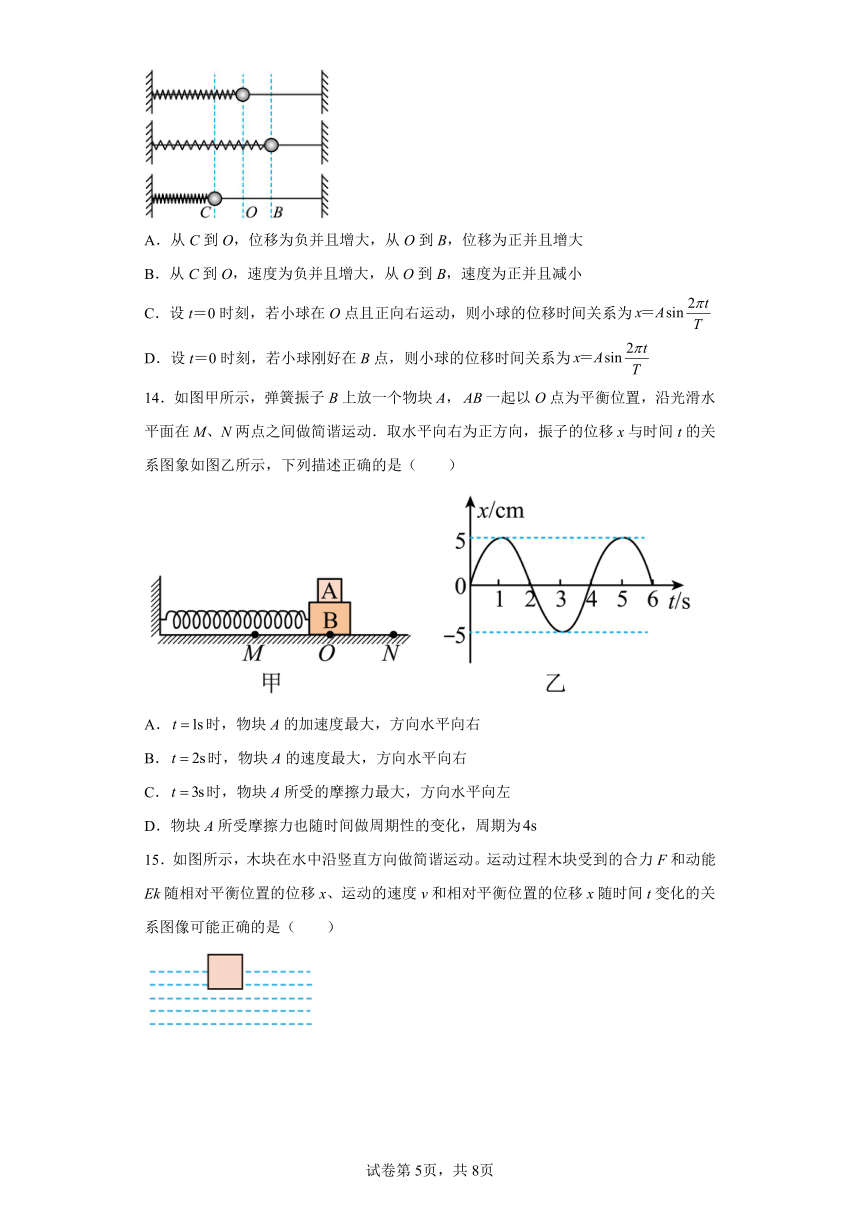
A.从C到O,位移为负并且增大,从O到B,位移为正并且增大
B.从C到O,速度为负并且增大,从O到B,速度为正并且减小
C.设t=0时刻,若小球在O点且正向右运动,则小球的位移时间关系为
D.设t=0时刻,若小球刚好在B点,则小球的位移时间关系为
14.如图甲所示,弹簧振子B上放一个物块A,一起以O点为平衡位置,沿光滑水平面在M、N两点之间做简谐运动.取水平向右为正方向,振子的位移x与时间t的关系图象如图乙所示,下列描述正确的是( )
A.时,物块A的加速度最大,方向水平向右
B.时,物块A的速度最大,方向水平向右
C.时,物块A所受的摩擦力最大,方向水平向左
D.物块A所受摩擦力也随时间做周期性的变化,周期为
15.如图所示,木块在水中沿竖直方向做简谐运动。运动过程木块受到的合力F和动能Ek随相对平衡位置的位移x、运动的速度v和相对平衡位置的位移x随时间t变化的关系图像可能正确的是( )
A. B.
C. D.
二、填空题
16.弹簧振子做简谐运动,通过M点时的速度为v,经1s第一次以相同的速度通过P点,又经过1s,振子第二次通过P点,振子在2s内的总路程为18cm,由已知条件可求得该弹簧振子的周期是________s,振幅是________cm。
17.甲物体完成15次全振动的时间内,乙物体恰好完成了3次全振动,则两个物体的周期之比为__________.
18.简谐运动的运动特征:衡位置时,x减小,v___________;远离平衡位置时,x都增大,v___________
19.水平弹簧振子,下端装有一根记录笔,在水平桌面上铺记录纸,当振子振动时,以速率v水平向左匀速拉动记录纸,记录笔在纸上留下如图所示的图像,、、、为纸上印记的位置坐标,则此弹簧振子的振幅为__________,周期为__________。
三、解答题
20.两木块A、B质量分别为m、2m,用劲度系数为k的轻弹簧连在一起,放在水平地面上,如图所示,用外力将木块A压下一段距离静止,释放后A在竖直方向做简谐运动,在A振动过程中,木块B刚好未离开地面。重力加速度为g,求:
(1)木块A的最大加速度;
(2)A的振幅。
21.一个小球和轻质弹簧组成的系统按的规律振动。
(1)求该振动的周期、频率、振幅和初相;
(2)另一简谐运动的表达式为,求它们的相位差。
22.如果表给出的是做简谐运动的物体的位移x、速度v与时刻的对应关系,T是振动周期,若甲表示位移,则哪一项表示相应的速度?若丁表示位移,则哪一项表示相应的速度?
物理量 时刻
0 T
甲 零 正向最大 零 负向最大 零
乙 零 负向最大 零 正向最大 零
丙 正向最大 零 负向最大 零 正向最大
丁 负向最大 零 正向最大 零 负向最大
23.分析如图所示的弹簧振子在一次振动中的运动情况,填好下表。
振子的运动
位移的方向、大小
速度的方向、大小
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【详解】
A.从O→B→O振子完成了半个全振动,故A错误;
BC.A到B运动时间是2 s,周期
因为
t=6s=1.5T
根据振子完成一次全振动通过的路程是4A,故从B开始经过6s,振子通过的路程是
S=1.5×4A=6A=6×10cm=60cm
故B正确C错误;
D.从O开始经过3 s即,振子处在位移最大的位置,故D错误;
故选B。
2.B
【详解】
因为
F=-kx
a=
故图丙可作为F-t、a-t图象;而y-t图像的斜率等于速度,可知v-t图象应为图乙。
故选B。
3.D
【详解】
在木板上由摆动着的漏斗中漏出的沙形成的曲线显示出摆的位移随时间变化的规律,即沙摆的振动图像。由于拉动木板的速度不同,所以N1、N2上两条曲线的时间轴(横轴)的单位长度代表的时间不等。如果确定了N1、N2上两条曲线的时间轴的单位长度与时间的对应关系后,就可以确定各条曲线代表的沙摆完成一次全振动所需的时间,即振动周期,从而可以确定T1、T2的关系。由题图可知,薄木板被匀速拉出的距离相同,且v2=2v1,则木板N1上时间轴单位长度代表的时间t1是木板N2上时间轴单位长度代表的时间t2的两倍,即
t1=2t2
由题图乙可知
T1=t1,T2=t2
从而得出
T1=4T2
故选D。
4.D
【详解】
A.振子从平衡位置O向N点运动过程中,偏离平衡位置的距离不断增大,加速度不断增大,速度不断减小,A错误;
B.根据振动图可知,弹簧振子的周期为
振子从M点运动到N点所用时间为半个周期
振子从M点运动到N点所用时间为,B错误;
C.由图可知,时弹簧振子向负方向运动,速度方向指向x轴的负方向,C错误;
D.结合振动图,当时,弹簧振子的回复力为
此时回复力的大小为,方向指向x轴的正方向,D正确。
故选D。
5.D
【详解】
A.由振动图像可以得知,振子的振动周期等于,A错误;
B.由周期与频率的关系公式,可得振子的振动频率等于
B错误;
C.在时刻,振子的位移是零,在平衡位置O点处,C错误;
D.由振动图像可知,在时刻,振子从平衡位置O点处开始向负方向的最大位移处a点振动,后又沿x轴正方向向平衡位置振动,在时刻,振子向右经O点,D正确。
故选D。
6.B
【详解】
A.圆心投影点为平衡点,最大位移为R,则振幅为R,故A错误;
B.当影子通过平衡点时的速度最大,此时其速度等于小球运动速度,即最大速度为,故B正确;
C.影子的振动周期应和小球做圆周运动的周期相同,即
故C错误;
D.影子初始位于平衡位置,位移表达式为
故D错误。
故选B。
7.C
【详解】
ABD.由图可知,在0s时刻,质点位移为正且最大,速度为0,振动系统势能最大,由
知加速度为负且最大;由图可知在0.3s时刻,质点位移为0,速度为正向最大,振动系统势能最小,加速度则为0,故ABD错误;
C.在时质点位移为零,位移正在从负变成正,所以回复力正在从正变成负,故C正确。
故选C。
8.C
【详解】
A.从O→B→O振子通过的路程是两个振幅,不是一次全振动,A错误;
B.由题,AB间距离为30cm,A到B运动时间为4s,则振幅
周期为
B错误;
C.从B开始经过6s,振子振动了四分之三个周期,通过的路程是
C正确;
D.从O开始经过6s,振子振动了四分之三个周期,振子处在最大位移处,D错误。
故选C。
9.C
【详解】
A.0~2s内质点的速度方向始终沿x轴负方向,故A不符合题意;
B.1~3s内质点的速度方向先沿x轴负方向,后沿x轴正方向,故B不符合题意;
C.2~4s内质点的速度方向始终沿x轴正方向,故C符合题意;
D.3~5s内质点的速度方向先沿x轴正方向,后沿x轴负方向,故D不符合题意。
故选C。
10.C
【详解】
A.当振子再次经过A时,不一定刚好经过一个周期,所以路程不一定是4倍振幅,A错误;
B.因为A点位置不确定,所以当振子再次经过A时,经过的时间可能半周期,也可能小于或大于半个周期,故B错误;
C.弹簧振子做简谐振动时加速度由回复力产生,当振子的加速度再次与零时刻的加速度相同时,由于方向也相同,所以偏离平衡位置的位移也相同,则一定又到达原来位置,故C正确;
D.根据运动的对称性,还有另一个位置跟位置A有相同的位移大小,但是对称点位移方向与A位置位移方向相反,所以另一个与A位置位移相同点不存在,故D错误。
故选C。
11.C
【详解】
物体振动的频率f=25Hz,则周期
简谐运动中,越衡位置,物体运动速度越大,如果经过两点时速度方向相同,物体从一侧最大位移的中点运动到平衡位置的时间小于,从平衡位置运动到另一侧最大位移的中点所用的时间也小于,则总时间小于,即小于0.01s;如果经过两点时速度方向相反,则由简谐运动的对称性知,物体恰好运动了半个周期,运动时间为
故C正确,ABD错误。
故选C。
12.D
【详解】
A.振幅是位移的最大值的大小,故振幅为8 cm,而周期是完成一次全振动的时间,振动周期为4 s,故A错误;
B.第2 s末振子的速度为零,故B错误;
C.从第1 s末到第2 s末振子的位移逐渐增大,速度逐渐减小,振子做减速运动,故C错误;
D.第3 s末振子的位移为零,经过平衡位置,故速度最大,且方向为正,故D正确。
故选D。
13.C
【详解】
A.简谐运动的位移是相对平衡位置的位移;从C到O,位移向左,为负,并且减小;从O到B,位移为正并且增大,A错误;
B.从C到O,衡位置,速度为正并且增大;从O到B,远离平衡位置,速度为正,并且减小,B错误;
C.设t=0时刻,若小球在O点且正向右运动,则小球的位移与时间关系为正弦函数关系,所以有
由角速度和周期关系
可得
C正确;
D.设t=0时刻,若小球刚好在B点,则小球的位移与时间关系为余弦函数关系,结合C中分析,所以
D错误。
故选C。
14.D
【详解】
A.时,振子到达最右端,此时位移最大,则物块A的加速度最大,方向指向平衡位置,即水平向左,选项A错误;
B.时,物块A的速度最大,方向水平向左,选项B错误;
C.时,振子到达最左端,则此时加速度向右最大,则物块A所受的摩擦力最大,方向水平向右,选项C错误;
D.根据
物块A所受摩擦力
则物块A受的摩擦力也随时间做周期性的变化,周期为,选项D正确。
故选D。
15.C
【详解】
A.根据简谐运动的规律可得,浮力与重力平衡,则有
则运动过程木块受到的合力F应该过二四象限,A错误;
B.随着增大,势能增大,由能量守恒可得,动能应减小,B错误;
CD.因为木块在水中沿竖直方向做简谐运动,故运动的速度v和相对平衡位置的位移x随时间t变化的关系图像都应该是三角函数的波形,D错误,C正确。
故选C。
16. 4s或 9cm或3
由题中“弹簧振子做简谐运动”可知,本题考查简谐振动周期和振幅,根据简谐振动的周期性和对称性可分析本题.
【详解】
[1][2] 过M、P两点的速度相同,M、P两点一定关于平衡位置O对称。
由简谐运动的周期性和往复性可知道,若通过M点时向平衡位置方向运动,则2s为半个周期,则
T=4s
18cm=2A
得
A=9cm
若通过M点时向平衡位置的反方向运动,则
T=s
18cm=6A
得
A=3cm
17.1:5
【详解】
根据频率是单位时间内完成全振动的次数,可知甲乙的频率之比为,由 可得:振动周期之比为,故答案是1:5
18. 增大 减小
【详解】
[1][2] 简谐运动的运动特征:衡位置时,x减小,v增大;远离平衡位置时,x都增大,v减小.
19.
【详解】
由图知振幅
记录纸匀速运动,为2.5个波长,则周期
20.(1)3g;(2)
【详解】
(1)由于A做简谐运动,在最高点和最低点加速度最大,在最高点时,木块B刚好对地面的压力为零,此时弹簧弹力
F=kx1=2mg
对A物体,根据牛顿第二定律可得
F+mg=ma
木块A的最大加速度
a=3g
(2)在最高点弹簧的伸长量为
而平衡位置弹簧的压缩量
因此A的振幅为
21.(1),,,;(2)
【详解】
(1)已知,由
得
所以频率为
由可看出,振幅为
初相位为
(2)由
得
22.丙;甲
【详解】
简谐运动中速度与位移大小变化情况是相反的,即位移增大,速度减小,再分析方向关系即可,若甲表示位移,振子从平衡位置向正向最大位移处运动,速度从正向最大开始减小零,所以丙可以表示相应的速度;丁表示位移,位移从最大负向位移变化到零,振子从负向最大位移处向平衡位置运动,速度从零开始正向最大速度变化,所以甲表示相应的速度。
23.见解析所示
【详解】
弹簧振子在一次振动中的运动情况如图;
振子的运动
位移的方向、大小 向右减小 向左增大 向左减小 向右增大
速度的方向、大小 向左增大 向左减小 向右增大 向右减小
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间距离是20 cm,从A到B运动时间是2 s,则( )
A.从O→B→O振子做了一次全振动
B.从B开始经过6 s,振子通过的路程是60 cm
C.振动周期为2 s,振幅是10 cm
D.从O开始经过3 s,振子处在平衡位置
2.有一个在y方向上做简谐运动的物体,其振动图像如图所示。下列选项中v、F、a分别表示物体的速度、受到的回复力和加速度,关于图甲、乙、丙、丁的判断正确的是( )
A.甲可作为该物体的F—t图像 B.乙可作为该物体的v—t图像
C.丙可作为该物体的v—t图像 D.丁可作为该物体的a—t图像
3.如图甲所示是演示简谐运动图像的装置,当漏斗下面的薄木板N被匀速地拉出时,振动着的漏斗中漏出的沙在板上形成的曲线显示出摆的位移随时间变化的关系。板上的直线OO1代表时间轴,图乙中是两个摆中的沙在各自板上形成的曲线,若板N1和板N2拉动的速度v1和v2的关系为v2=2v1,则板N1、N2上曲线所代表的周期T1和T2的关系为( )
A.T2=T1 B.T2=2T1 C.T2=4T1 D.T2=T1
4.如图甲所示,一水平弹簧振子在M、N两点间沿x轴方向做简谐运动,以平衡位置O为坐标原点,向右为x轴正方向。振子的振动图像如图乙所示,其中时振子的位移为。已知弹簧劲度系数为15N/cm,则( )
A.振子从平衡位置O向N点运动过程中,加速度不断减小,速度不断减小
B.振子从M点运动到N点所用时间为9s
C.图乙中时振子的速度方向指向x轴的正方向
D.图乙中时振子所受的回复力大小为7.5N,方向指向x轴的正方向
5.如图甲所示,水平的光滑杆上有一弹簧振子,振子以O点为平衡位置,在a、b两点之间做简谐运动,取向右为正方向,其振动图像如图乙所示。由振动图像可以得知( )
A.振子的振动周期等于
B.振子的振动频率等于
C.在时刻,振子的位置在a点
D.在时刻,振子向右经过O点
6.如图所示,小球在竖直平面内以半径为、角速度为沿逆时针方向做匀速圆周运动,用竖直向下的平行光照射小球,观察到其影子在水平面上做简谐运动。取圆心投影点为原点,水平向右为正方向建立坐标系,从小球某次经最高点的时刻开始计时,关于影子的说法正确是( )
A.振幅为
B.振动过程中的最大速度为
C.振动周期为
D.位移表达式为
7.一质点做简谐运动的图像如图所示,则在0~0.4s内,下列结论中正确的是( )
A.质点速度最大而加速度为零的时刻分别是0、0.3s
B.质点速度为零而加速度为负方向最大值的时刻分别是0、0.3s
C.质点所受的回复力方向由正变负的时刻是0.3s
D.振动系统势能最大而加速度为正方向最大值的时刻是0.3s
8.如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间距离是30cm,从A到B运动时间是4s,则( )
A.从振了做了一次全振动
B.振动周期为4s,振幅是15cm
C.从B开始经过6s,振子通过的路程是45cm
D.从O开始经过6s,振子处在平衡位置
9.某质点的振动图像如图所示,该质点的速度方向始终沿x轴正方向的时间段为( )
A.t=0~2s B.t=1~3s C.t=2~4s D.t=3~5s
10.弹簧振子做简谐运动时,从振子经过某一位置A开始计时,则( )
A.当振子再次经过A时,已通过的路程一定是4倍振幅
B.当振子再次经过A时,经过的时间一定是半周期
C.当振子的加速度再次与零时刻的加速度相同时,一定又到达位置A
D.一定还有另外一个位置跟位置A有相同的位移
11.一个做简谐运动的物体,频率为25Hz,那么它从一侧最大位移的中点,振动到另一侧最大位移的中点所用的时间( )
A.等于0.01s B.一定小于0.01s C.可能大于0.01s D.无法确定
12.如图所示为某弹簧振子在0~5 s内的振动图像,由图可知,下列说法中正确的是( )
A.振动周期为5 s,振幅为8 cm
B.第2 s末振子的速度为负
C.从第1 s末到第2 s末振子在做加速运动
D.第3 s末振子的速度为正向的最大值
13.如图所示的弹簧振子水平放置,忽略各种阻力时,它将在COB之间来回往复的做简谐振动,其中O点为平衡位置,简谐振动的振幅为A,弹簧的劲度系数为k,原长为L,弹簧振子的周期为T,小球质量为m,且规定向右为位移的正方向。请由此判断下列说法正确的是( )
A.从C到O,位移为负并且增大,从O到B,位移为正并且增大
B.从C到O,速度为负并且增大,从O到B,速度为正并且减小
C.设t=0时刻,若小球在O点且正向右运动,则小球的位移时间关系为
D.设t=0时刻,若小球刚好在B点,则小球的位移时间关系为
14.如图甲所示,弹簧振子B上放一个物块A,一起以O点为平衡位置,沿光滑水平面在M、N两点之间做简谐运动.取水平向右为正方向,振子的位移x与时间t的关系图象如图乙所示,下列描述正确的是( )
A.时,物块A的加速度最大,方向水平向右
B.时,物块A的速度最大,方向水平向右
C.时,物块A所受的摩擦力最大,方向水平向左
D.物块A所受摩擦力也随时间做周期性的变化,周期为
15.如图所示,木块在水中沿竖直方向做简谐运动。运动过程木块受到的合力F和动能Ek随相对平衡位置的位移x、运动的速度v和相对平衡位置的位移x随时间t变化的关系图像可能正确的是( )
A. B.
C. D.
二、填空题
16.弹簧振子做简谐运动,通过M点时的速度为v,经1s第一次以相同的速度通过P点,又经过1s,振子第二次通过P点,振子在2s内的总路程为18cm,由已知条件可求得该弹簧振子的周期是________s,振幅是________cm。
17.甲物体完成15次全振动的时间内,乙物体恰好完成了3次全振动,则两个物体的周期之比为__________.
18.简谐运动的运动特征:衡位置时,x减小,v___________;远离平衡位置时,x都增大,v___________
19.水平弹簧振子,下端装有一根记录笔,在水平桌面上铺记录纸,当振子振动时,以速率v水平向左匀速拉动记录纸,记录笔在纸上留下如图所示的图像,、、、为纸上印记的位置坐标,则此弹簧振子的振幅为__________,周期为__________。
三、解答题
20.两木块A、B质量分别为m、2m,用劲度系数为k的轻弹簧连在一起,放在水平地面上,如图所示,用外力将木块A压下一段距离静止,释放后A在竖直方向做简谐运动,在A振动过程中,木块B刚好未离开地面。重力加速度为g,求:
(1)木块A的最大加速度;
(2)A的振幅。
21.一个小球和轻质弹簧组成的系统按的规律振动。
(1)求该振动的周期、频率、振幅和初相;
(2)另一简谐运动的表达式为,求它们的相位差。
22.如果表给出的是做简谐运动的物体的位移x、速度v与时刻的对应关系,T是振动周期,若甲表示位移,则哪一项表示相应的速度?若丁表示位移,则哪一项表示相应的速度?
物理量 时刻
0 T
甲 零 正向最大 零 负向最大 零
乙 零 负向最大 零 正向最大 零
丙 正向最大 零 负向最大 零 正向最大
丁 负向最大 零 正向最大 零 负向最大
23.分析如图所示的弹簧振子在一次振动中的运动情况,填好下表。
振子的运动
位移的方向、大小
速度的方向、大小
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【详解】
A.从O→B→O振子完成了半个全振动,故A错误;
BC.A到B运动时间是2 s,周期
因为
t=6s=1.5T
根据振子完成一次全振动通过的路程是4A,故从B开始经过6s,振子通过的路程是
S=1.5×4A=6A=6×10cm=60cm
故B正确C错误;
D.从O开始经过3 s即,振子处在位移最大的位置,故D错误;
故选B。
2.B
【详解】
因为
F=-kx
a=
故图丙可作为F-t、a-t图象;而y-t图像的斜率等于速度,可知v-t图象应为图乙。
故选B。
3.D
【详解】
在木板上由摆动着的漏斗中漏出的沙形成的曲线显示出摆的位移随时间变化的规律,即沙摆的振动图像。由于拉动木板的速度不同,所以N1、N2上两条曲线的时间轴(横轴)的单位长度代表的时间不等。如果确定了N1、N2上两条曲线的时间轴的单位长度与时间的对应关系后,就可以确定各条曲线代表的沙摆完成一次全振动所需的时间,即振动周期,从而可以确定T1、T2的关系。由题图可知,薄木板被匀速拉出的距离相同,且v2=2v1,则木板N1上时间轴单位长度代表的时间t1是木板N2上时间轴单位长度代表的时间t2的两倍,即
t1=2t2
由题图乙可知
T1=t1,T2=t2
从而得出
T1=4T2
故选D。
4.D
【详解】
A.振子从平衡位置O向N点运动过程中,偏离平衡位置的距离不断增大,加速度不断增大,速度不断减小,A错误;
B.根据振动图可知,弹簧振子的周期为
振子从M点运动到N点所用时间为半个周期
振子从M点运动到N点所用时间为,B错误;
C.由图可知,时弹簧振子向负方向运动,速度方向指向x轴的负方向,C错误;
D.结合振动图,当时,弹簧振子的回复力为
此时回复力的大小为,方向指向x轴的正方向,D正确。
故选D。
5.D
【详解】
A.由振动图像可以得知,振子的振动周期等于,A错误;
B.由周期与频率的关系公式,可得振子的振动频率等于
B错误;
C.在时刻,振子的位移是零,在平衡位置O点处,C错误;
D.由振动图像可知,在时刻,振子从平衡位置O点处开始向负方向的最大位移处a点振动,后又沿x轴正方向向平衡位置振动,在时刻,振子向右经O点,D正确。
故选D。
6.B
【详解】
A.圆心投影点为平衡点,最大位移为R,则振幅为R,故A错误;
B.当影子通过平衡点时的速度最大,此时其速度等于小球运动速度,即最大速度为,故B正确;
C.影子的振动周期应和小球做圆周运动的周期相同,即
故C错误;
D.影子初始位于平衡位置,位移表达式为
故D错误。
故选B。
7.C
【详解】
ABD.由图可知,在0s时刻,质点位移为正且最大,速度为0,振动系统势能最大,由
知加速度为负且最大;由图可知在0.3s时刻,质点位移为0,速度为正向最大,振动系统势能最小,加速度则为0,故ABD错误;
C.在时质点位移为零,位移正在从负变成正,所以回复力正在从正变成负,故C正确。
故选C。
8.C
【详解】
A.从O→B→O振子通过的路程是两个振幅,不是一次全振动,A错误;
B.由题,AB间距离为30cm,A到B运动时间为4s,则振幅
周期为
B错误;
C.从B开始经过6s,振子振动了四分之三个周期,通过的路程是
C正确;
D.从O开始经过6s,振子振动了四分之三个周期,振子处在最大位移处,D错误。
故选C。
9.C
【详解】
A.0~2s内质点的速度方向始终沿x轴负方向,故A不符合题意;
B.1~3s内质点的速度方向先沿x轴负方向,后沿x轴正方向,故B不符合题意;
C.2~4s内质点的速度方向始终沿x轴正方向,故C符合题意;
D.3~5s内质点的速度方向先沿x轴正方向,后沿x轴负方向,故D不符合题意。
故选C。
10.C
【详解】
A.当振子再次经过A时,不一定刚好经过一个周期,所以路程不一定是4倍振幅,A错误;
B.因为A点位置不确定,所以当振子再次经过A时,经过的时间可能半周期,也可能小于或大于半个周期,故B错误;
C.弹簧振子做简谐振动时加速度由回复力产生,当振子的加速度再次与零时刻的加速度相同时,由于方向也相同,所以偏离平衡位置的位移也相同,则一定又到达原来位置,故C正确;
D.根据运动的对称性,还有另一个位置跟位置A有相同的位移大小,但是对称点位移方向与A位置位移方向相反,所以另一个与A位置位移相同点不存在,故D错误。
故选C。
11.C
【详解】
物体振动的频率f=25Hz,则周期
简谐运动中,越衡位置,物体运动速度越大,如果经过两点时速度方向相同,物体从一侧最大位移的中点运动到平衡位置的时间小于,从平衡位置运动到另一侧最大位移的中点所用的时间也小于,则总时间小于,即小于0.01s;如果经过两点时速度方向相反,则由简谐运动的对称性知,物体恰好运动了半个周期,运动时间为
故C正确,ABD错误。
故选C。
12.D
【详解】
A.振幅是位移的最大值的大小,故振幅为8 cm,而周期是完成一次全振动的时间,振动周期为4 s,故A错误;
B.第2 s末振子的速度为零,故B错误;
C.从第1 s末到第2 s末振子的位移逐渐增大,速度逐渐减小,振子做减速运动,故C错误;
D.第3 s末振子的位移为零,经过平衡位置,故速度最大,且方向为正,故D正确。
故选D。
13.C
【详解】
A.简谐运动的位移是相对平衡位置的位移;从C到O,位移向左,为负,并且减小;从O到B,位移为正并且增大,A错误;
B.从C到O,衡位置,速度为正并且增大;从O到B,远离平衡位置,速度为正,并且减小,B错误;
C.设t=0时刻,若小球在O点且正向右运动,则小球的位移与时间关系为正弦函数关系,所以有
由角速度和周期关系
可得
C正确;
D.设t=0时刻,若小球刚好在B点,则小球的位移与时间关系为余弦函数关系,结合C中分析,所以
D错误。
故选C。
14.D
【详解】
A.时,振子到达最右端,此时位移最大,则物块A的加速度最大,方向指向平衡位置,即水平向左,选项A错误;
B.时,物块A的速度最大,方向水平向左,选项B错误;
C.时,振子到达最左端,则此时加速度向右最大,则物块A所受的摩擦力最大,方向水平向右,选项C错误;
D.根据
物块A所受摩擦力
则物块A受的摩擦力也随时间做周期性的变化,周期为,选项D正确。
故选D。
15.C
【详解】
A.根据简谐运动的规律可得,浮力与重力平衡,则有
则运动过程木块受到的合力F应该过二四象限,A错误;
B.随着增大,势能增大,由能量守恒可得,动能应减小,B错误;
CD.因为木块在水中沿竖直方向做简谐运动,故运动的速度v和相对平衡位置的位移x随时间t变化的关系图像都应该是三角函数的波形,D错误,C正确。
故选C。
16. 4s或 9cm或3
由题中“弹簧振子做简谐运动”可知,本题考查简谐振动周期和振幅,根据简谐振动的周期性和对称性可分析本题.
【详解】
[1][2] 过M、P两点的速度相同,M、P两点一定关于平衡位置O对称。
由简谐运动的周期性和往复性可知道,若通过M点时向平衡位置方向运动,则2s为半个周期,则
T=4s
18cm=2A
得
A=9cm
若通过M点时向平衡位置的反方向运动,则
T=s
18cm=6A
得
A=3cm
17.1:5
【详解】
根据频率是单位时间内完成全振动的次数,可知甲乙的频率之比为,由 可得:振动周期之比为,故答案是1:5
18. 增大 减小
【详解】
[1][2] 简谐运动的运动特征:衡位置时,x减小,v增大;远离平衡位置时,x都增大,v减小.
19.
【详解】
由图知振幅
记录纸匀速运动,为2.5个波长,则周期
20.(1)3g;(2)
【详解】
(1)由于A做简谐运动,在最高点和最低点加速度最大,在最高点时,木块B刚好对地面的压力为零,此时弹簧弹力
F=kx1=2mg
对A物体,根据牛顿第二定律可得
F+mg=ma
木块A的最大加速度
a=3g
(2)在最高点弹簧的伸长量为
而平衡位置弹簧的压缩量
因此A的振幅为
21.(1),,,;(2)
【详解】
(1)已知,由
得
所以频率为
由可看出,振幅为
初相位为
(2)由
得
22.丙;甲
【详解】
简谐运动中速度与位移大小变化情况是相反的,即位移增大,速度减小,再分析方向关系即可,若甲表示位移,振子从平衡位置向正向最大位移处运动,速度从正向最大开始减小零,所以丙可以表示相应的速度;丁表示位移,位移从最大负向位移变化到零,振子从负向最大位移处向平衡位置运动,速度从零开始正向最大速度变化,所以甲表示相应的速度。
23.见解析所示
【详解】
弹簧振子在一次振动中的运动情况如图;
振子的运动
位移的方向、大小 向右减小 向左增大 向左减小 向右增大
速度的方向、大小 向左增大 向左减小 向右增大 向右减小
答案第1页,共2页
答案第1页,共2页
