3.2决定导体电阻大小的因素 同步练习(Word版含解析)
文档属性
| 名称 | 3.2决定导体电阻大小的因素 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 404.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览




文档简介
粤教版(2019)必修三 3.2 决定导体电阻大小的因素
一、单选题
1.下列说法中正确的是( )
A.连接电路用的导线一般用合金来制作
B.电炉、电阻器的电阻丝一般用合金来制作
C.电阻温度计一般用电阻率几乎不受温度影响的合金来制作
D.标准电阻一般用电阻率随温度变化而显著变化的金属材料制作
2.两根完全相同的金属裸导线,如果把其中的一根均匀拉长到原来的3倍,把另一根对折后绞合起来,则两导线的电阻之比为( )
A.6:1 B.9:1 C.18:1 D.36:1
3.在温度不变的情况下,先将一根粗细均匀,阻值为16Ω的电阻丝等分成四段,每段电阻为R1;再将这四段电阻丝并联,并联后总电阻为R2。则R1与R2的大小依次为( )
A.1Ω,4Ω B.4Ω,1Ω C.2Ω,8Ω D.2Ω,0.5Ω
4.如图所示,R1和R2是材料相同、厚度相同、表面均为正方形的导体,R1边长为2L,R2边长为L,若R1的阻值为16Ω,则R2的阻值为( )
A.4Ω B.8Ω C.16Ω D.64Ω
5.用可拉伸的材料制成长为l、直径为d的圆柱形容器,在其中充满电解液,经测量可知电解液的阻值为8Ω。假设电解液的阻值的变化趋势与金属丝的阻值的变化趋势相同,在保持容器体积不变的情况下,将该容器的长度均匀地拉长到原来的1.25倍,则此时该电解液的阻值为( )
A.5.12Ω B.6.4Ω C.12.5Ω D.25Ω
6.两根完全相同的金属导线,如果把其中的一根均匀拉长到原来的3倍,然后给它们分别加上相同电压,则在同一时间内,通过它们横截面的电荷量之比为( )
A.3:1 B.1:3 C.9:1 D.1:9
7.如图所示,厚薄均匀的矩形金属薄片边长为,,当将与接入电压恒为的电路时,电流为,若将A与接入电路中时电流仍为,则接入的电压为( )
A. B. C. D.
8.和是材料相同,厚度相同,表面都为正方形的导体,但的边长是的2倍,把它们分别连接在如图电路的端,接时电压表的读数为,接时电压表的读数为,下列判断正确的是( )
A. B.
C. D.
9.两根不同材料制成的均匀电阻丝,长度之比l1∶l2=5∶2,直径之比d1∶d2=2∶1,给它们加相同的电压,通过它们的电流之比为I1∶I2=3∶2,则它们的电阻率的比值为( )
A. B. C. D.
10.下列说法中正确的是( )
A.导体中电荷的定向移动形成电流
B.电流有方向,物理学中规定负电荷定向移动的方向为电流的方向
C.电阻率大的导体,电阻一定大
D.电阻率与导体的长度和横截面积有关
11.下列关于公式和的分析正确的是 ( )
A.由公式可知,导体的电阻与导体两端的电压成正比,与通过导体的电流成反比
B.由公式可知,当导体电阻一定时,通过导体的电流与导体两端的电压成正比
C.由公式可知,导体的电阻率与导体的电阻成正比
D.由公式可知,将一粗细均匀的导体拉长到原来的2倍时,其电阻也为原来的2倍
12.如图所示,两个用相同材料制成的上表面均为正方形的长方体导体甲、乙,高度均为,甲、乙上表面边长分别为,则( )
A.从图示电流方向看,甲、乙电阻之比为
B.从图示电流方向看,甲、乙电阻之比为
C.若电流方向均为竖直向下,甲、乙电阻之比为
D.若电流方向均为竖直向下,甲、乙电阻之比
13.超纯水(Ultrapurewater)又称UP水,是为了研制超纯材料(半导体原件材料、纳米精细陶瓷材料等),应用蒸馏、去离子化、反渗透技术或其它适当的超临界精细技术生产出来的水,其电阻率大于18MΩ·cm,或接近18.3MΩ·cm极限值(25°C)。以下说法中,正确的是( )
A.电阻率和温度并无关系
B.超纯水电阻率大,导电能力非常微弱
C.超纯水电阻率和存放容器的横截面积有关
D.去离子化制作超纯水,制作前、后的电阻率并无变化
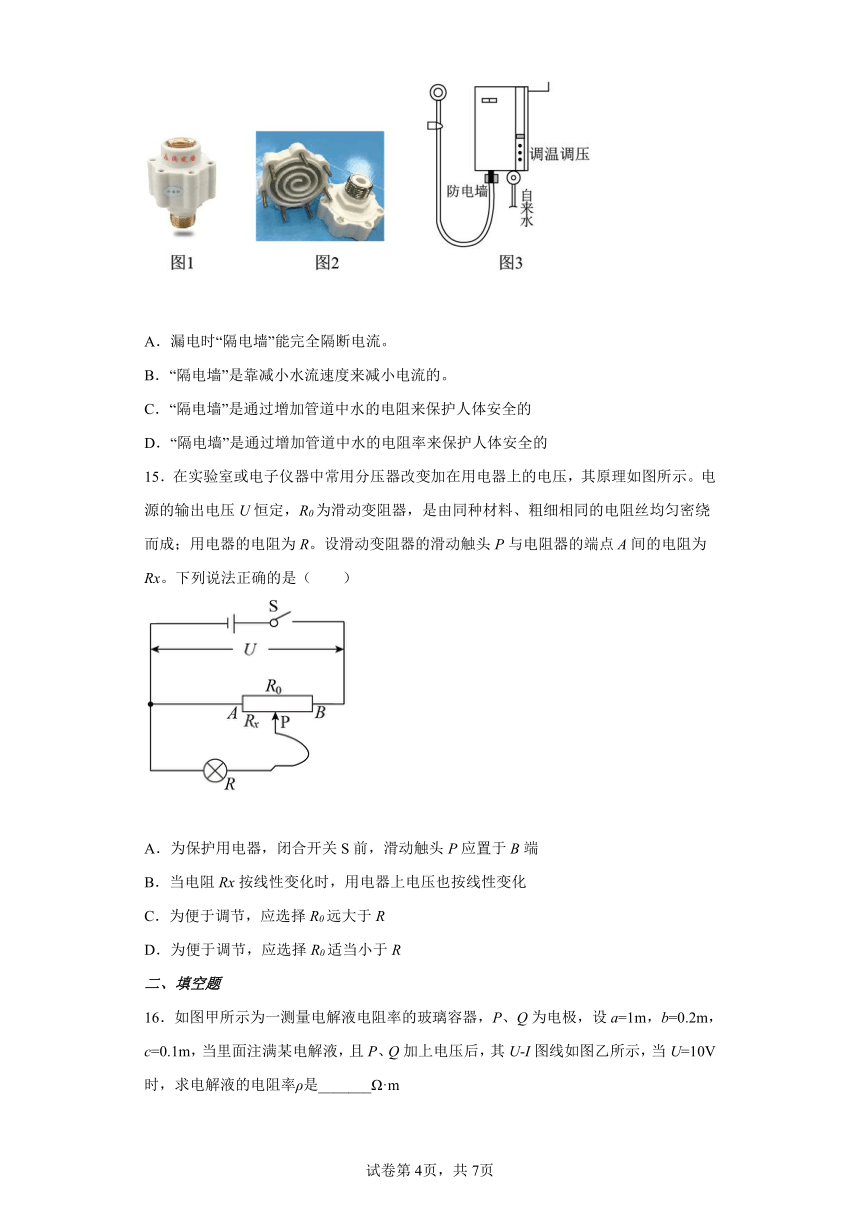
14.家用电热水器,在使用时具有漏电危险,当发生漏电时,电流会经过水管中的水,流到人体而发生意外事故。“隔电墙”可以在--定程度上保护人体的安全,其装置如图(1),其内部结构是一个螺旋状的绝缘管道,结构如图(2),它实则上是将水管的水道变得更细更长,安装位置如图(3)。下列分析正确的是( )
A.漏电时“隔电墙”能完全隔断电流。
B.“隔电墙”是靠减小水流速度来减小电流的。
C.“隔电墙”是通过增加管道中水的电阻来保护人体安全的
D.“隔电墙”是通过增加管道中水的电阻率来保护人体安全的
15.在实验室或电子仪器中常用分压器改变加在用电器上的电压,其原理如图所示。电源的输出电压U恒定,R0为滑动变阻器,是由同种材料、粗细相同的电阻丝均匀密绕而成;用电器的电阻为R。设滑动变阻器的滑动触头P与电阻器的端点A间的电阻为Rx。下列说法正确的是( )
A.为保护用电器,闭合开关S前,滑动触头P应置于B端
B.当电阻Rx按线性变化时,用电器上电压也按线性变化
C.为便于调节,应选择R0远大于R
D.为便于调节,应选择R0适当小于R
二、填空题
16.如图甲所示为一测量电解液电阻率的玻璃容器,P、Q为电极,设a=1m,b=0.2m,c=0.1m,当里面注满某电解液,且P、Q加上电压后,其U-I图线如图乙所示,当U=10V时,求电解液的电阻率ρ是_______Ω·m
17.导体的电阻:同种材料的导体,其电阻R与它的长度l成___________,与它的横截面积S成___________;导体电阻还与构成它的材料有关。
18.两根由同种材料制成的均匀电阻丝A、B串联在电路中,A的长度为L,直径为d; B的长度为2L,直径为2d,那么通电后,A、B在相同的时间内产生的热量之比为QA:QB=_________
三、解答题
19.A、B两地相距L,在两地间沿直线铺有通讯电缆,它是由两条并在一起彼此绝缘的均匀导线组成的,通常称为双线电缆。在一次事故中经检查断定是电缆上某处的绝缘保护层损坏,导致两导线之间漏电,相当于该处电缆的两导线之间接入一个电阻。检查人员经过下面的测量可以确定损坏处的位置:
(1)将B端双线断开,在A处测出双线两端间的电阻RA;
(2)将A端的双线断开,在B处测出双线两端的电阻RB;
(3)在A端的双线间加一已知电压UA,在B端间用内阻很大的电压表测量出两线间的电压UB.
试由以上测量结果确定损坏处距A的距离。
20.如图所示,AB和A′B′是长度均为L=2 km的两根输电线(1 km电阻值为1 Ω),若发现在距离A和A′等远的两点C和C′间发生漏电,相当于在两点间连接了一个电阻.接入电压为U=90 V的电源:当电源接在A、A′间时,测得B、B′间电压为UB=72 V;当电源接在B、B′间时,测得A、A′间电压为UA=45 V.由此可知A与C相距多远?
21.如图所示,电子由静止开始经加速电场加速后,沿平行于板面的方向射入偏转电场,并从另一侧射出,已知电子质量为m,电荷量为e,加速电场电压为U0偏转电场可看做匀强电场,极板间电压为U,极板长度为L,板间距为d。
(1)忽略电子所受重力,求从电场射出时沿垂直板面方向的偏转距离Δy;
(2)分析物理量的数量级,是解决物理问题的常用办法。在解决(1)问时忽略电子所受重力,请利用下列数据分析说明其原因。已知U=2.0×102V,d=4.0×10-2m,m=9.1×10-31kg,e=1.6×10-19C,g=10m/s2;
(3)经典电磁理论认为:当金属导体两端电压稳定后,导体中产生恒定电场,这种恒定电场的性质与静电场相同。由于恒定电场的作用,导体内自由电子定向移动的速率增加,而运动过程中会与导体内不动的粒子发生碰撞从而减速,因此自由电子定向移动的平均速率不随时间变化。金属电阻反映的是定向运动的自由电子与不动的粒子的碰撞。假设碰撞后自由电子定向移动的速度全部消失,碰撞时间不计。某种金属中单位体积内的自由电子数量为n,自由电子的质量为m,带电量为e。现取由该种金属制成的长为L,横截面积为S的圆柱形金属导体,将其两端加上恒定电压U,自由电子连续两次与不动的粒子碰撞的时间间隔平均值为t0,请从电阻的定义式出发,推导影响电阻率ρ的因素。
22.对于同一物理问题,常常可以从宏观与微观两个不同角度进行研究,找出其内在联系,从而更加深刻地理解其物理本质。一段长为l、横截面积为S的细金属直导线,单位体积内有n个自由电子,电子电荷量为e、质量为m。
(1)该导线通有电流时,假设自由电子定向移动的速率恒为v。
① 求导线中的电流I;
②为了更精细地描述电流的分布情况,引入了电流面密度j,电流面密度被定义为单位面积的电流强度,求电流面密度j的表达式;
③经典物理学认为,金属的电阻源于定向运动的自由电子与金属离子(即金属原子失去电子后的剩余部分)的碰撞,该碰撞过程将对电子的定向移动形成一定的阻碍作用,该作用可等效为施加在电子上的一个沿导线的平均阻力。若电子受到的平均阻力大小与电子定向移动的速率成正比,比例系数为k。请根据以上描述构建物理模型,求出金属导体的电阻率ρ的微观表达式。
(2*)将上述导线弯成一个闭合圆线圈,若该不带电的圆线圈绕通过圆心且垂直于线圈平面的轴匀速率转动,线圈中不会有电流通过,若线圈转动的线速度大小发生变化,线圈中会有电流通过,这个现象首先由斯泰瓦和托尔曼在1917年发现,被称为斯泰瓦—托尔曼效应。这一现象可解释为:当线圈转动的线速度大小均匀变化时,由于惯性,自由电子与线圈中的金属离子间产生定向的相对运动,从而形成电流。若此线圈在匀速转动的过程中突然停止转动,由于电子在导线中运动会受到沿导线的平均阻力,所以只会形成短暂的电流。已知电子受到的沿导线的平均阻力满足(1)问中的规律,求此线圈以由角速度ω匀速转动突然停止转动(减速时间可忽略不计)之后,通过线圈导线横截面的电荷量Q。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【详解】
A.为了减小导线上的功率损耗,连接电路的导线一般要用纯金属制作, 故A错误;
B.电炉和电阻器是为了在相同条件下获得较大的电阻值, 一般用合金制作,故B正确;
C.制作电阻温度计的材料的电阻率需要随温度变化有显著的变化,故C错误;
D.标准电阻的阻值需要在一定温度范围内几乎保持不变,所以一般用电阻率几乎不受温度影响的材料制作,故D错误。
故选B。
2.D
【详解】
设原来的电阻为R,根据电阻定律
得,把其中的一根均匀拉长到原来的3倍,根据体积不变可知,其横截面积变为原来的 ,故电阻变为原来的9倍,即9R。把另一根对折后绞合起来,则长度变为原来的一半,横截面积变为原来的2倍,则电阻变为原来的 ,即为。故两导线的电阻之比为36:1。
故选D。
3.B
【详解】
一根粗细均匀的电阻丝,将它等分成四段,每段的长度减小为四分之一,横截面积和电阻率一定,故电阻减小为四分之一,为
再将这四段电阻丝并联起来,横截面积增加为4倍,根据电阻定律
故选B。
4.C
【详解】
由公式可知,长度比为2:1,横截面积比为2:1,所以两电阻比为1:1
故选C。
5.C
【详解】
根据电阻定律
保持容器的体积不变,电解液仍充满整个容器,将容器的长度均匀地拉长到原来的1.25倍,则容器的截面积变为原来的,电阻变为
故选C。
6.D
【详解】
设原来导线的电阻为R,其中的一根均匀拉长到原来的3倍,横截面积变为原来的,根据电阻定律,可知拉长导线的电阻为
则两根导线的电阻之比为9:1,由于电压相等,根据欧姆定律,则电流比为1:9,根据可知,相同时间内通过导线的电荷量之比为1:9。
故选D。
7.D
【详解】
设金属薄片的厚度为d,根据电阻定律
得
可得
根据欧姆定律,电流相同时,电压与电阻成正比,故两次电压之比为,故将AB接入电路时,接入的电压为9U。
故选D。
8.C
【详解】
R1和R2是材料相同、厚度相同、上下表面都为正方形的导体,根据电阻定律可知
可见,厚度相同、上下表面都为正方形的导体,尽管尺寸不同,但电阻相同,所以
R1=R2
因为电阻相等,所以电压表的读数也相等,所以
U1=U2
故C正确,ABD错误。
故选C。
9.D
【详解】
根据可知,两电阻丝的电阻之比为,两电阻丝的横截面积之比为,根据电阻定律得,所以
故选D。
10.A
【详解】
A.导体中电荷的定向移动形成电流,故A正确;
B.电流有方向,物理学中规定正电荷定向移动的方向为电流的方向,故B错误;
C.由电阻定律公式可知,导体的电阻不仅和电阻率有关,还和导体长度和横截面积有关,故电阻率大,电阻不一定大,故C错误;
D.电阻率仅与材料本身有关,与长度和横截面积无关,故D错误。
故选A。
11.B
【详解】
A.公式为电阻的定义式,能计算电阻的大小,但导体的电阻与导体两端的电压、通过导体的电流无关,A错误;
B.由公式可知,当导体电阻一定时,通过导体的电流与导体两端的电压成正比,B正确;
C.导体的电阻率由材料、温度等因素决定,与导体的电阻无关,C错误;
D.由公式可知,将一粗细均匀的导体拉长到原来的2倍时,横截面积变为原来的一半,则其电阻为原来的4倍,D错误。
故选B。
12.B
【详解】
AB.由可知:当电流方向如图示时
,
则
故A错误,B正确;
CD.当电流方向均为竖直向下时
,
则有
故CD错误。
故选B。
13.B
【详解】
A.电阻率和温度有关,故A错误;
B.超纯水电阻率大,导电能力非常微弱,故B正确;
C.超纯水的电阻率和存放容器的横截面积无关,故C错误;
D.去离子化制作超纯水,制作后的超纯水中离子浓度减小,导电能力减弱,电阻率增大,故D错误。
故选B。
14.C
【详解】
根据电阻定律可知
水的电阻率不变,在该情况下,将水流变长,横截面积变小来增大电阻,减小电流,从而对人体起到保护作用。
故选C。
15.D
【详解】
A.用电器与Rx并联,等于Rx两端电压,为保护用电器,闭合开关S前,滑动触头P应置于A端,让用电器两端电压等于零,A错误;
B.用电器上电压为
解得
当电阻Rx按线性变化时,比例系数 一定是变化的,用电器上电压一定按非线性变化,B错误;
CD.由电阻定律 得, ,R0越小的滑动变阻器的导线越粗,S越大,单位长度的电阻值 越小,调解时电阻变化越缓慢,越方便调解,所以为便于调节,应选择R0适当小于R,D正确,C错误。
故选D。
16.40
【详解】
由图乙可求得电解液的电阻为;由图甲可知电解液长为,截面积为,结合电阻定律可得
17. 正比 反比
【详解】
略
18.2:1
【详解】
试题分析:直径比为1:2,则横截面积比为1:4,根据电阻定律,,电阻之比为2:1,根据,电流相等,则热量之比为2:1.
考点:电阻定律
点评:本题的关键知道串联电路电流相等,以及电阻定律和焦耳定律.
19.
【详解】
设电缆每单位长度的电阻为r,漏电处的电阻为R,漏电处距A的距离为x。则A、A′间的电阻
RA=2rx+R
B、B′间的电阻
RB=2r(L-x)+R
根据欧姆定律有
联立解得
20.LAC=0.4 km
【详解】
根据题意,将电路变成图甲所示电路,其中R1=R1′,R2=R2′,当AA′接90V,BB′电压为72V,如图乙所示(电压表内阻太大,R2和R′2的作用忽略,丙图同理)此时R1、R1′、R串联,
∵在串联电路中电阻和电压成正比,
∴R1:R:R1′=9V:72V:9V=1:8:1---------------①
同理,当BB′接90V,AA′电压为45V,如图丙所示,此时R2、R2′、R串联,
∵在串联电路中电阻和电压成正比,
∴R2:R:R2′=22.5V:45V:22.5V=1:2:1=4:8:4---②
联立①②可得:
R1:R2=1:4
由题意,
RAB=2km×=2Ω=R1+R2
∴R1=0.4Ω,R2=1.6Ω
AC相距
s==0.4km.
【点睛】
本题考查了串联电路的电阻、电流特点和欧姆定律的应用;解决本题的关键:一是明白电压表测得是漏电电阻两端的电压,二是知道电路相当于三个串联.
21.(1) ;(2)见详解;(3)见详解
【详解】
(1)电子经过加速电场后,由动能定理
可得
电子在偏转电场中运动的时间为
电子在偏转电场中的加速度
偏转距离
(2) 考虑重力和电场力的数量级,有重力
电场力为
由于
因此不需要考虑重力;
(3)金属两端加上恒定电压U后,电子受的电场力为
电子在电场中加速时间为t0,由动量定理
可得
则电子定向移动的平均速率为
金属中的电流为
由电阻的定义式
可得
其中为定值,即电阻率ρ,所以影响电阻率的因素有单位体积内的电子个数,自由电子连续两次与不动的粒子碰撞的时间间隔平均值为t0。
22.(1)① ;②;③ (2)
【详解】
(1)①导线中的电流
;
②电流面密度
;
③取长度为L一段导体,则电子做定向移动时满足电场力与阻力相等,即
而
联立解得
(2)设线圈经过时间 t停止运动,则对内部的粒子,由动量定理:
其中
则
;
而
联立可得
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列说法中正确的是( )
A.连接电路用的导线一般用合金来制作
B.电炉、电阻器的电阻丝一般用合金来制作
C.电阻温度计一般用电阻率几乎不受温度影响的合金来制作
D.标准电阻一般用电阻率随温度变化而显著变化的金属材料制作
2.两根完全相同的金属裸导线,如果把其中的一根均匀拉长到原来的3倍,把另一根对折后绞合起来,则两导线的电阻之比为( )
A.6:1 B.9:1 C.18:1 D.36:1
3.在温度不变的情况下,先将一根粗细均匀,阻值为16Ω的电阻丝等分成四段,每段电阻为R1;再将这四段电阻丝并联,并联后总电阻为R2。则R1与R2的大小依次为( )
A.1Ω,4Ω B.4Ω,1Ω C.2Ω,8Ω D.2Ω,0.5Ω
4.如图所示,R1和R2是材料相同、厚度相同、表面均为正方形的导体,R1边长为2L,R2边长为L,若R1的阻值为16Ω,则R2的阻值为( )
A.4Ω B.8Ω C.16Ω D.64Ω
5.用可拉伸的材料制成长为l、直径为d的圆柱形容器,在其中充满电解液,经测量可知电解液的阻值为8Ω。假设电解液的阻值的变化趋势与金属丝的阻值的变化趋势相同,在保持容器体积不变的情况下,将该容器的长度均匀地拉长到原来的1.25倍,则此时该电解液的阻值为( )
A.5.12Ω B.6.4Ω C.12.5Ω D.25Ω
6.两根完全相同的金属导线,如果把其中的一根均匀拉长到原来的3倍,然后给它们分别加上相同电压,则在同一时间内,通过它们横截面的电荷量之比为( )
A.3:1 B.1:3 C.9:1 D.1:9
7.如图所示,厚薄均匀的矩形金属薄片边长为,,当将与接入电压恒为的电路时,电流为,若将A与接入电路中时电流仍为,则接入的电压为( )
A. B. C. D.
8.和是材料相同,厚度相同,表面都为正方形的导体,但的边长是的2倍,把它们分别连接在如图电路的端,接时电压表的读数为,接时电压表的读数为,下列判断正确的是( )
A. B.
C. D.
9.两根不同材料制成的均匀电阻丝,长度之比l1∶l2=5∶2,直径之比d1∶d2=2∶1,给它们加相同的电压,通过它们的电流之比为I1∶I2=3∶2,则它们的电阻率的比值为( )
A. B. C. D.
10.下列说法中正确的是( )
A.导体中电荷的定向移动形成电流
B.电流有方向,物理学中规定负电荷定向移动的方向为电流的方向
C.电阻率大的导体,电阻一定大
D.电阻率与导体的长度和横截面积有关
11.下列关于公式和的分析正确的是 ( )
A.由公式可知,导体的电阻与导体两端的电压成正比,与通过导体的电流成反比
B.由公式可知,当导体电阻一定时,通过导体的电流与导体两端的电压成正比
C.由公式可知,导体的电阻率与导体的电阻成正比
D.由公式可知,将一粗细均匀的导体拉长到原来的2倍时,其电阻也为原来的2倍
12.如图所示,两个用相同材料制成的上表面均为正方形的长方体导体甲、乙,高度均为,甲、乙上表面边长分别为,则( )
A.从图示电流方向看,甲、乙电阻之比为
B.从图示电流方向看,甲、乙电阻之比为
C.若电流方向均为竖直向下,甲、乙电阻之比为
D.若电流方向均为竖直向下,甲、乙电阻之比
13.超纯水(Ultrapurewater)又称UP水,是为了研制超纯材料(半导体原件材料、纳米精细陶瓷材料等),应用蒸馏、去离子化、反渗透技术或其它适当的超临界精细技术生产出来的水,其电阻率大于18MΩ·cm,或接近18.3MΩ·cm极限值(25°C)。以下说法中,正确的是( )
A.电阻率和温度并无关系
B.超纯水电阻率大,导电能力非常微弱
C.超纯水电阻率和存放容器的横截面积有关
D.去离子化制作超纯水,制作前、后的电阻率并无变化
14.家用电热水器,在使用时具有漏电危险,当发生漏电时,电流会经过水管中的水,流到人体而发生意外事故。“隔电墙”可以在--定程度上保护人体的安全,其装置如图(1),其内部结构是一个螺旋状的绝缘管道,结构如图(2),它实则上是将水管的水道变得更细更长,安装位置如图(3)。下列分析正确的是( )
A.漏电时“隔电墙”能完全隔断电流。
B.“隔电墙”是靠减小水流速度来减小电流的。
C.“隔电墙”是通过增加管道中水的电阻来保护人体安全的
D.“隔电墙”是通过增加管道中水的电阻率来保护人体安全的
15.在实验室或电子仪器中常用分压器改变加在用电器上的电压,其原理如图所示。电源的输出电压U恒定,R0为滑动变阻器,是由同种材料、粗细相同的电阻丝均匀密绕而成;用电器的电阻为R。设滑动变阻器的滑动触头P与电阻器的端点A间的电阻为Rx。下列说法正确的是( )
A.为保护用电器,闭合开关S前,滑动触头P应置于B端
B.当电阻Rx按线性变化时,用电器上电压也按线性变化
C.为便于调节,应选择R0远大于R
D.为便于调节,应选择R0适当小于R
二、填空题
16.如图甲所示为一测量电解液电阻率的玻璃容器,P、Q为电极,设a=1m,b=0.2m,c=0.1m,当里面注满某电解液,且P、Q加上电压后,其U-I图线如图乙所示,当U=10V时,求电解液的电阻率ρ是_______Ω·m
17.导体的电阻:同种材料的导体,其电阻R与它的长度l成___________,与它的横截面积S成___________;导体电阻还与构成它的材料有关。
18.两根由同种材料制成的均匀电阻丝A、B串联在电路中,A的长度为L,直径为d; B的长度为2L,直径为2d,那么通电后,A、B在相同的时间内产生的热量之比为QA:QB=_________
三、解答题
19.A、B两地相距L,在两地间沿直线铺有通讯电缆,它是由两条并在一起彼此绝缘的均匀导线组成的,通常称为双线电缆。在一次事故中经检查断定是电缆上某处的绝缘保护层损坏,导致两导线之间漏电,相当于该处电缆的两导线之间接入一个电阻。检查人员经过下面的测量可以确定损坏处的位置:
(1)将B端双线断开,在A处测出双线两端间的电阻RA;
(2)将A端的双线断开,在B处测出双线两端的电阻RB;
(3)在A端的双线间加一已知电压UA,在B端间用内阻很大的电压表测量出两线间的电压UB.
试由以上测量结果确定损坏处距A的距离。
20.如图所示,AB和A′B′是长度均为L=2 km的两根输电线(1 km电阻值为1 Ω),若发现在距离A和A′等远的两点C和C′间发生漏电,相当于在两点间连接了一个电阻.接入电压为U=90 V的电源:当电源接在A、A′间时,测得B、B′间电压为UB=72 V;当电源接在B、B′间时,测得A、A′间电压为UA=45 V.由此可知A与C相距多远?
21.如图所示,电子由静止开始经加速电场加速后,沿平行于板面的方向射入偏转电场,并从另一侧射出,已知电子质量为m,电荷量为e,加速电场电压为U0偏转电场可看做匀强电场,极板间电压为U,极板长度为L,板间距为d。
(1)忽略电子所受重力,求从电场射出时沿垂直板面方向的偏转距离Δy;
(2)分析物理量的数量级,是解决物理问题的常用办法。在解决(1)问时忽略电子所受重力,请利用下列数据分析说明其原因。已知U=2.0×102V,d=4.0×10-2m,m=9.1×10-31kg,e=1.6×10-19C,g=10m/s2;
(3)经典电磁理论认为:当金属导体两端电压稳定后,导体中产生恒定电场,这种恒定电场的性质与静电场相同。由于恒定电场的作用,导体内自由电子定向移动的速率增加,而运动过程中会与导体内不动的粒子发生碰撞从而减速,因此自由电子定向移动的平均速率不随时间变化。金属电阻反映的是定向运动的自由电子与不动的粒子的碰撞。假设碰撞后自由电子定向移动的速度全部消失,碰撞时间不计。某种金属中单位体积内的自由电子数量为n,自由电子的质量为m,带电量为e。现取由该种金属制成的长为L,横截面积为S的圆柱形金属导体,将其两端加上恒定电压U,自由电子连续两次与不动的粒子碰撞的时间间隔平均值为t0,请从电阻的定义式出发,推导影响电阻率ρ的因素。
22.对于同一物理问题,常常可以从宏观与微观两个不同角度进行研究,找出其内在联系,从而更加深刻地理解其物理本质。一段长为l、横截面积为S的细金属直导线,单位体积内有n个自由电子,电子电荷量为e、质量为m。
(1)该导线通有电流时,假设自由电子定向移动的速率恒为v。
① 求导线中的电流I;
②为了更精细地描述电流的分布情况,引入了电流面密度j,电流面密度被定义为单位面积的电流强度,求电流面密度j的表达式;
③经典物理学认为,金属的电阻源于定向运动的自由电子与金属离子(即金属原子失去电子后的剩余部分)的碰撞,该碰撞过程将对电子的定向移动形成一定的阻碍作用,该作用可等效为施加在电子上的一个沿导线的平均阻力。若电子受到的平均阻力大小与电子定向移动的速率成正比,比例系数为k。请根据以上描述构建物理模型,求出金属导体的电阻率ρ的微观表达式。
(2*)将上述导线弯成一个闭合圆线圈,若该不带电的圆线圈绕通过圆心且垂直于线圈平面的轴匀速率转动,线圈中不会有电流通过,若线圈转动的线速度大小发生变化,线圈中会有电流通过,这个现象首先由斯泰瓦和托尔曼在1917年发现,被称为斯泰瓦—托尔曼效应。这一现象可解释为:当线圈转动的线速度大小均匀变化时,由于惯性,自由电子与线圈中的金属离子间产生定向的相对运动,从而形成电流。若此线圈在匀速转动的过程中突然停止转动,由于电子在导线中运动会受到沿导线的平均阻力,所以只会形成短暂的电流。已知电子受到的沿导线的平均阻力满足(1)问中的规律,求此线圈以由角速度ω匀速转动突然停止转动(减速时间可忽略不计)之后,通过线圈导线横截面的电荷量Q。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【详解】
A.为了减小导线上的功率损耗,连接电路的导线一般要用纯金属制作, 故A错误;
B.电炉和电阻器是为了在相同条件下获得较大的电阻值, 一般用合金制作,故B正确;
C.制作电阻温度计的材料的电阻率需要随温度变化有显著的变化,故C错误;
D.标准电阻的阻值需要在一定温度范围内几乎保持不变,所以一般用电阻率几乎不受温度影响的材料制作,故D错误。
故选B。
2.D
【详解】
设原来的电阻为R,根据电阻定律
得,把其中的一根均匀拉长到原来的3倍,根据体积不变可知,其横截面积变为原来的 ,故电阻变为原来的9倍,即9R。把另一根对折后绞合起来,则长度变为原来的一半,横截面积变为原来的2倍,则电阻变为原来的 ,即为。故两导线的电阻之比为36:1。
故选D。
3.B
【详解】
一根粗细均匀的电阻丝,将它等分成四段,每段的长度减小为四分之一,横截面积和电阻率一定,故电阻减小为四分之一,为
再将这四段电阻丝并联起来,横截面积增加为4倍,根据电阻定律
故选B。
4.C
【详解】
由公式可知,长度比为2:1,横截面积比为2:1,所以两电阻比为1:1
故选C。
5.C
【详解】
根据电阻定律
保持容器的体积不变,电解液仍充满整个容器,将容器的长度均匀地拉长到原来的1.25倍,则容器的截面积变为原来的,电阻变为
故选C。
6.D
【详解】
设原来导线的电阻为R,其中的一根均匀拉长到原来的3倍,横截面积变为原来的,根据电阻定律,可知拉长导线的电阻为
则两根导线的电阻之比为9:1,由于电压相等,根据欧姆定律,则电流比为1:9,根据可知,相同时间内通过导线的电荷量之比为1:9。
故选D。
7.D
【详解】
设金属薄片的厚度为d,根据电阻定律
得
可得
根据欧姆定律,电流相同时,电压与电阻成正比,故两次电压之比为,故将AB接入电路时,接入的电压为9U。
故选D。
8.C
【详解】
R1和R2是材料相同、厚度相同、上下表面都为正方形的导体,根据电阻定律可知
可见,厚度相同、上下表面都为正方形的导体,尽管尺寸不同,但电阻相同,所以
R1=R2
因为电阻相等,所以电压表的读数也相等,所以
U1=U2
故C正确,ABD错误。
故选C。
9.D
【详解】
根据可知,两电阻丝的电阻之比为,两电阻丝的横截面积之比为,根据电阻定律得,所以
故选D。
10.A
【详解】
A.导体中电荷的定向移动形成电流,故A正确;
B.电流有方向,物理学中规定正电荷定向移动的方向为电流的方向,故B错误;
C.由电阻定律公式可知,导体的电阻不仅和电阻率有关,还和导体长度和横截面积有关,故电阻率大,电阻不一定大,故C错误;
D.电阻率仅与材料本身有关,与长度和横截面积无关,故D错误。
故选A。
11.B
【详解】
A.公式为电阻的定义式,能计算电阻的大小,但导体的电阻与导体两端的电压、通过导体的电流无关,A错误;
B.由公式可知,当导体电阻一定时,通过导体的电流与导体两端的电压成正比,B正确;
C.导体的电阻率由材料、温度等因素决定,与导体的电阻无关,C错误;
D.由公式可知,将一粗细均匀的导体拉长到原来的2倍时,横截面积变为原来的一半,则其电阻为原来的4倍,D错误。
故选B。
12.B
【详解】
AB.由可知:当电流方向如图示时
,
则
故A错误,B正确;
CD.当电流方向均为竖直向下时
,
则有
故CD错误。
故选B。
13.B
【详解】
A.电阻率和温度有关,故A错误;
B.超纯水电阻率大,导电能力非常微弱,故B正确;
C.超纯水的电阻率和存放容器的横截面积无关,故C错误;
D.去离子化制作超纯水,制作后的超纯水中离子浓度减小,导电能力减弱,电阻率增大,故D错误。
故选B。
14.C
【详解】
根据电阻定律可知
水的电阻率不变,在该情况下,将水流变长,横截面积变小来增大电阻,减小电流,从而对人体起到保护作用。
故选C。
15.D
【详解】
A.用电器与Rx并联,等于Rx两端电压,为保护用电器,闭合开关S前,滑动触头P应置于A端,让用电器两端电压等于零,A错误;
B.用电器上电压为
解得
当电阻Rx按线性变化时,比例系数 一定是变化的,用电器上电压一定按非线性变化,B错误;
CD.由电阻定律 得, ,R0越小的滑动变阻器的导线越粗,S越大,单位长度的电阻值 越小,调解时电阻变化越缓慢,越方便调解,所以为便于调节,应选择R0适当小于R,D正确,C错误。
故选D。
16.40
【详解】
由图乙可求得电解液的电阻为;由图甲可知电解液长为,截面积为,结合电阻定律可得
17. 正比 反比
【详解】
略
18.2:1
【详解】
试题分析:直径比为1:2,则横截面积比为1:4,根据电阻定律,,电阻之比为2:1,根据,电流相等,则热量之比为2:1.
考点:电阻定律
点评:本题的关键知道串联电路电流相等,以及电阻定律和焦耳定律.
19.
【详解】
设电缆每单位长度的电阻为r,漏电处的电阻为R,漏电处距A的距离为x。则A、A′间的电阻
RA=2rx+R
B、B′间的电阻
RB=2r(L-x)+R
根据欧姆定律有
联立解得
20.LAC=0.4 km
【详解】
根据题意,将电路变成图甲所示电路,其中R1=R1′,R2=R2′,当AA′接90V,BB′电压为72V,如图乙所示(电压表内阻太大,R2和R′2的作用忽略,丙图同理)此时R1、R1′、R串联,
∵在串联电路中电阻和电压成正比,
∴R1:R:R1′=9V:72V:9V=1:8:1---------------①
同理,当BB′接90V,AA′电压为45V,如图丙所示,此时R2、R2′、R串联,
∵在串联电路中电阻和电压成正比,
∴R2:R:R2′=22.5V:45V:22.5V=1:2:1=4:8:4---②
联立①②可得:
R1:R2=1:4
由题意,
RAB=2km×=2Ω=R1+R2
∴R1=0.4Ω,R2=1.6Ω
AC相距
s==0.4km.
【点睛】
本题考查了串联电路的电阻、电流特点和欧姆定律的应用;解决本题的关键:一是明白电压表测得是漏电电阻两端的电压,二是知道电路相当于三个串联.
21.(1) ;(2)见详解;(3)见详解
【详解】
(1)电子经过加速电场后,由动能定理
可得
电子在偏转电场中运动的时间为
电子在偏转电场中的加速度
偏转距离
(2) 考虑重力和电场力的数量级,有重力
电场力为
由于
因此不需要考虑重力;
(3)金属两端加上恒定电压U后,电子受的电场力为
电子在电场中加速时间为t0,由动量定理
可得
则电子定向移动的平均速率为
金属中的电流为
由电阻的定义式
可得
其中为定值,即电阻率ρ,所以影响电阻率的因素有单位体积内的电子个数,自由电子连续两次与不动的粒子碰撞的时间间隔平均值为t0。
22.(1)① ;②;③ (2)
【详解】
(1)①导线中的电流
;
②电流面密度
;
③取长度为L一段导体,则电子做定向移动时满足电场力与阻力相等,即
而
联立解得
(2)设线圈经过时间 t停止运动,则对内部的粒子,由动量定理:
其中
则
;
而
联立可得
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 静电场的描述
- 第一节 静电现象
- 第二节 库仑定律
- 第三节 电场 电场强度
- 第四节 电势能与电势
- 第五节 电势差及其与电场强度的关系
- 第二章 静电场的应用
- 第一节 电容器与电容
- 第二节 带电粒子在电场中的运动
- 第三节 静电的利用与防护
- 第三章 恒定电流
- 第一节 导体的伏安特性曲线
- 第二节 决定导体电阻大小的因素
- 第三节 测量金属丝的电阻率
- 第四节 电阻的串联和并联
- 第四章 闭合电路
- 第一节 常见的电路元器件
- 第二节 闭合电路的欧姆定律
- 第三节 测量电源的电动势和内阻
- 第四节 练习使用多用电表
- 第五节 家庭电路与安全用电
- 第五章 电能与能源的可持续发展
- 第一节 电路中的能量
- 第二节 能源的利用方式
- 第三节 能量的转化与守恒
- 第四节 能源与环境
- 第六章 电磁现象与电磁波
- 第一节 磁现象与磁场
- 第二节 磁感应强度
- 第三节 电磁感应现象
- 第四节 电磁波及其应用
- 第五节 量子化现象
