1.4质谱仪与回旋加速器 同步练习(Word版含解析)
文档属性
| 名称 | 1.4质谱仪与回旋加速器 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-08 03:23:09 | ||
图片预览



文档简介
人教版(2019)选择性必修二 1.4 质谱仪与回旋加速器 同步练习
试卷副标题
考试范围:xxx;考试时间:100分钟;命题人:xxx
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
1.如图所示,初速度为零的粒子和质子分别经过相同的加速电场后,沿垂直磁感应强度方向进入匀强磁场Ⅰ区域,接着进入匀强磁场Ⅱ区域。已知磁场Ⅰ、Ⅱ的磁感应强度大小分别为、,且,下列说法正确的是( )
A.粒子自磁场Ⅰ区域进入磁场Ⅱ区域线速度大小均减小,角速度均减小
B.粒子自磁场Ⅰ区域进入磁场Ⅱ区域向心加速度大小均变小,周期均变小
C.无论在磁场Ⅰ区域还是在磁场Ⅱ区域中,粒子的轨迹半径均小于质子轨迹半径
D.无论在磁场Ⅰ区域还是在磁场Ⅱ区域中,粒子的周期均大于质子的周期
2.如图所示,M、N为一对水平放置的平行金属板,一带电粒子以平行于金属板方向的速度v穿过平行金属板。若在两板间存在互相垂直的匀强电场和匀强磁场,可使带电粒子的运动不发生偏转,做匀速直线运动。不计粒子所受的重力,则以下叙述正确的是( )
A.若改变粒子的电性,即使它以同样速度v射入该区域,其运动方向也一定会发生偏转
B.粒子无论带上何种电荷,只要以同样的速度v入射,都不会发生偏转
C.若带电粒子的入射速度v′>v,它将一定向上偏转
D.若带电粒子的入射速度v′3.如图所示,三个粒子a、b、c分别以、、的速率进入速度选择器,a粒子打在速度选择器的上极板,b和c粒子沿直线运动后进入偏转磁场,b粒子打在点,c粒子打在点,不计粒子重力,下列说法正确的是( )
A.上极板比下极板的电势低 B.一定有
C.a、b粒子一定都带负电 D.b粒子的比荷一定大于c粒子的比荷
4.霍尔效应可用来测量血流速度,其原理如图所示。在动脉血管上下两侧安装电极,左右两侧加以磁场,毫伏表测出上下两极的电压为U。则( )
A.上电极电势一定低于下电极
B.若血液中负离子较多时,上电极电势低于下电极
C.毫伏表的示数U与血液的流速成正比
D.毫伏表的示数U与血液中正负离子的电荷量成正比
5.如图所示,用洛伦兹力演示仪研究带电粒子在匀强磁场中的运动,以虚线表示电极K释放出来的电子束的径迹。在施加磁场之前,电子经加速后沿直线运动,如图甲所示;施加磁场后电子束的径迹,如图乙所示;再调节演示仪可得到图丙所示的电子束径迹。下列说法正确的是( )
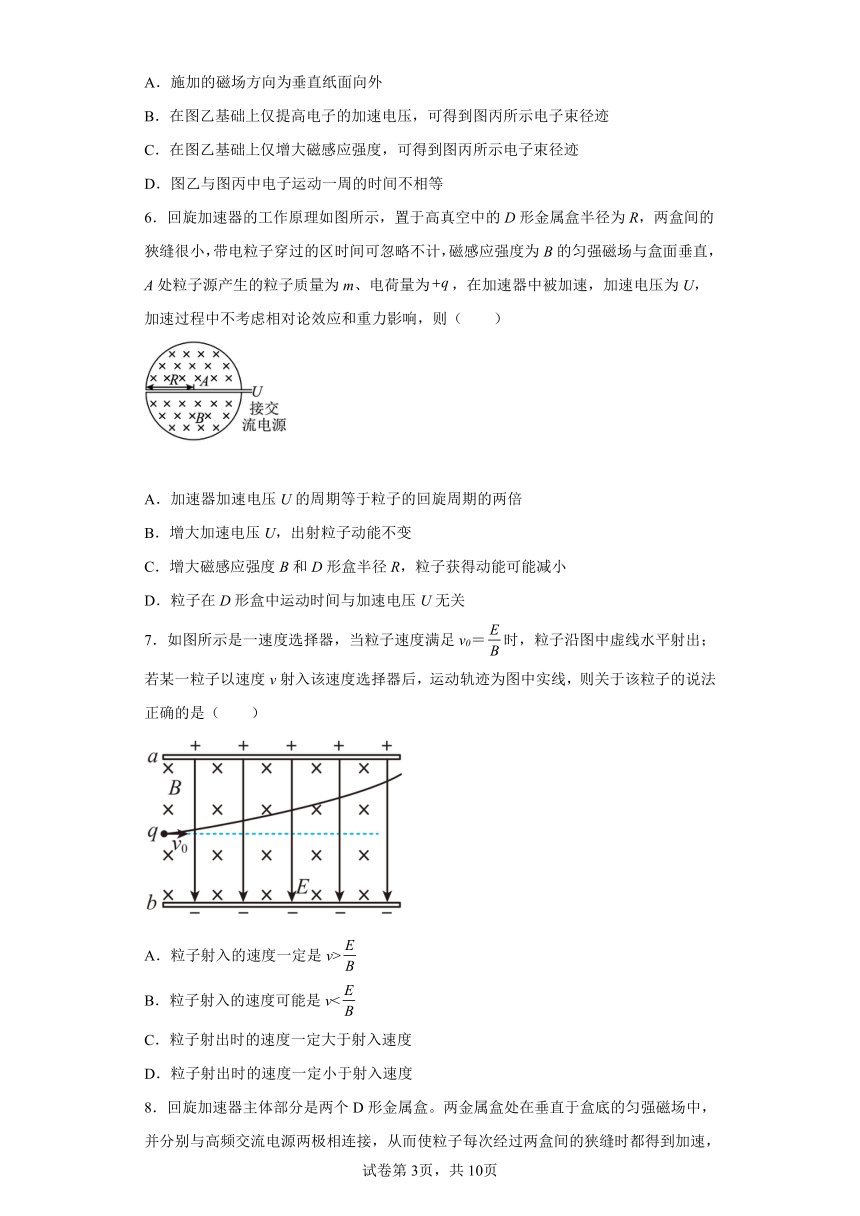
A.施加的磁场方向为垂直纸面向外
B.在图乙基础上仅提高电子的加速电压,可得到图丙所示电子束径迹
C.在图乙基础上仅增大磁感应强度,可得到图丙所示电子束径迹
D.图乙与图丙中电子运动一周的时间不相等
6.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狹缝很小,带电粒子穿过的区时间可忽略不计,磁感应强度为B的匀强磁场与盒面垂直,A处粒子源产生的粒子质量为m、电荷量为,在加速器中被加速,加速电压为U,加速过程中不考虑相对论效应和重力影响,则( )
A.加速器加速电压U的周期等于粒子的回旋周期的两倍
B.增大加速电压U,出射粒子动能不变
C.增大磁感应强度B和D形盒半径R,粒子获得动能可能减小
D.粒子在D形盒中运动时间与加速电压U无关
7.如图所示是一速度选择器,当粒子速度满足v0=时,粒子沿图中虚线水平射出;若某一粒子以速度v射入该速度选择器后,运动轨迹为图中实线,则关于该粒子的说法正确的是( )
A.粒子射入的速度一定是v>
B.粒子射入的速度可能是v<
C.粒子射出时的速度一定大于射入速度
D.粒子射出时的速度一定小于射入速度
8.回旋加速器主体部分是两个D形金属盒。两金属盒处在垂直于盒底的匀强磁场中,并分别与高频交流电源两极相连接,从而使粒子每次经过两盒间的狭缝时都得到加速,如图所示。在粒子质量不变和D形盒外径R固定的情况下,下列说法正确的是( )
A.粒子每次在磁场中偏转的时间随着加速次数的增加而增大
B.粒子在电场中加速时每次获得的能量相同
C.增大高频交流的电压,则可以增大粒子最后偏转出D形盒时的动能
D.将磁感应强度B减小,则可以增大粒子最后偏转出D形盒时的动能
9.回旋加速器是用来加速带电粒子使它获得很大动能的装置,其核心部分是两个D型金属盒,置于匀强磁场中,两盒分别与高频电源相连。下列说法正确的是( )
A.粒子被加速后的最大速度与D型金属盒的半径无关
B.粒子被加速后的最大动能随高频电源的加速电压的增大而增大
C.高频电源频率由粒子的质量、电量和磁感应强度决定
D.高频电源频率与粒子的质量、电量和磁感应强度无关
10.如图所示带电小球a以一定的初速度v0竖直向上抛出,能够达到的最大高度为ha;带电小球b在水平方向的匀强磁场以相同的初速度v0竖直向上抛出,上升的最大高度为hb;带电小球c在水平方向的匀强电场以相同的初速度v0竖直向上抛出,上升的最大高度为hc,不计空气阻力,三个小球的质量相等,则正确的是( )
A.它们上升的最大高度关系为ha=hb=hc
B.它们上升的最大高度关系为hbC.到达最大高度时,c小球机械能最小
D.到达最大高度时,b小球动能最小
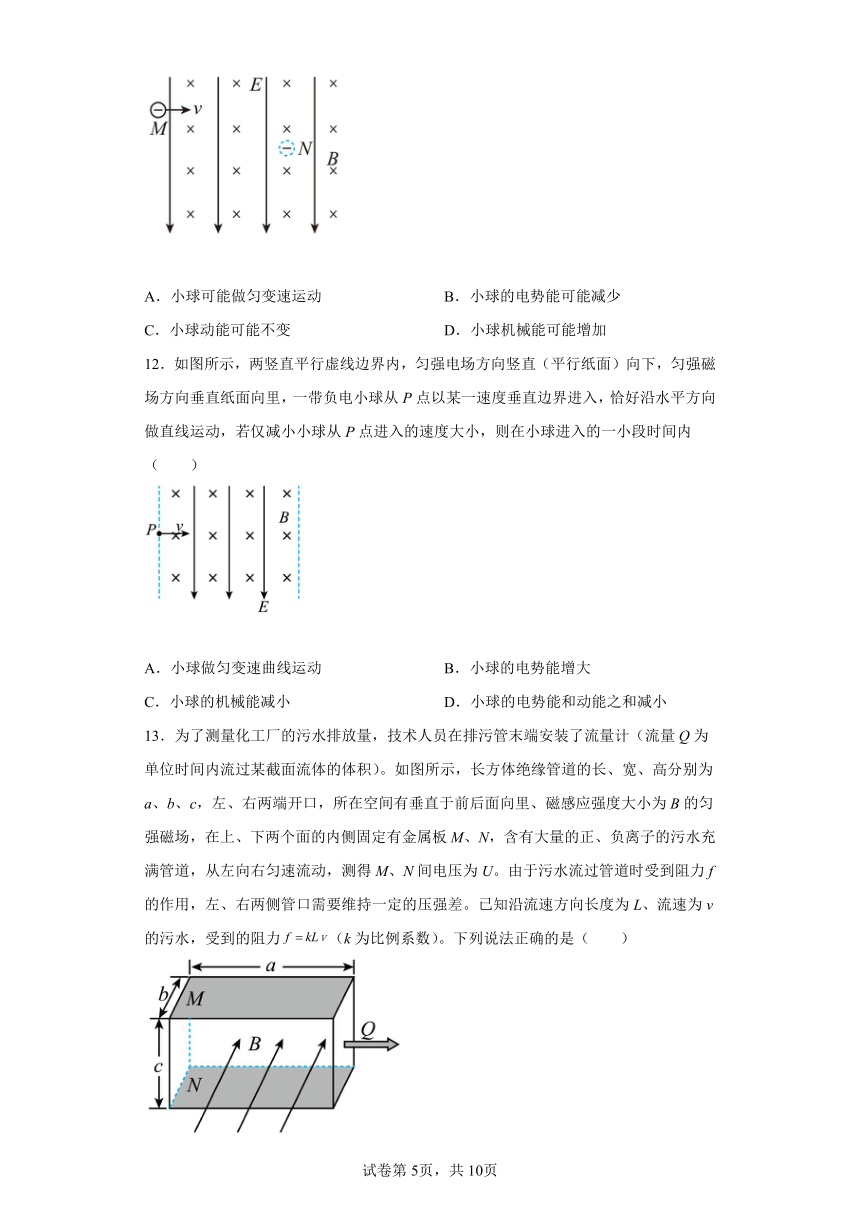
11.如图所示,空间某处存在竖直向下的匀强电场和垂直纸面向里的匀强磁场,一个带负电的金属小球从M点水平射入场区,经一段时间运动到N点,关于小球由M到N的运动,下列说法正确的是( )
A.小球可能做匀变速运动 B.小球的电势能可能减少
C.小球动能可能不变 D.小球机械能可能增加
12.如图所示,两竖直平行虚线边界内,匀强电场方向竖直(平行纸面)向下,匀强磁场方向垂直纸面向里,一带负电小球从P点以某一速度垂直边界进入,恰好沿水平方向做直线运动,若仅减小小球从P点进入的速度大小,则在小球进入的一小段时间内( )
A.小球做匀变速曲线运动 B.小球的电势能增大
C.小球的机械能减小 D.小球的电势能和动能之和减小
13.为了测量化工厂的污水排放量,技术人员在排污管末端安装了流量计(流量Q为单位时间内流过某截面流体的体积)。如图所示,长方体绝缘管道的长、宽、高分别为a、b、c,左、右两端开口,所在空间有垂直于前后面向里、磁感应强度大小为B的匀强磁场,在上、下两个面的内侧固定有金属板M、N,含有大量的正、负离子的污水充满管道,从左向右匀速流动,测得M、N间电压为U。由于污水流过管道时受到阻力f的作用,左、右两侧管口需要维持一定的压强差。已知沿流速方向长度为L、流速为v的污水,受到的阻力(k为比例系数)。下列说法正确的是( )
A.污水的流量
B.金属板的电势低于金属板的电势
C.电压与污水中的离子浓度有关
D.左、右两侧管口的压强差为
14.图甲是回旋加速器的示意图,粒子出口处如图所示.图乙是回旋加速器所用的交变电压随时间的变化规律。某物理学习小组在学习了回旋加速器原理之后,想利用同一回旋加速器分别加速两种带正电的粒子,所带电荷量分别为q1、q2,质量分别为m1、m2。保持交变电压随时间变化的规律不变,需要调整所加磁场的磁感应强度的大小,则( )
A.所加磁场的磁感应强度大小之比为
B.粒子获得的最大动能之比为
C.粒子的加速次数之比为
D.粒子在回旋加速器中的运动时间之比为
15.如图所示,MDN为绝缘材料制成的半径为R的光滑竖直半圆环,置于磁感应强度为B,方向垂直纸面向外的匀强磁场中,一质量为m,带正电可看成质点的小圆环套在大圆环上,从M点无初速下落,D为圆环最低点,N点与M点等高,小圆环在运动的过程中,下列说法中正确的是( )
A.小环由M滑到D点所用时间与由D滑到N点所用时间相同
B.小环滑到D点时速率满足
C.小环滑到D点时对圆环轨道的弹力一定小于mg
D.如果改变圆环的半径,小圆环从M滑到D点时在D点对圆环轨道的弹力随圆环半径的增大而减小
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
16.磁流体发电是一项新兴技术,它可以把气体的内能直接转化为电能。下图是磁流体发电机的装置:A、B组成一对平行电极,两极间距为d,内有磁感应强度为B的匀强磁场,现持续将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而整体呈中性)垂直喷射入磁场,每个离子的速度为v,电荷量大小为q,忽略两极之间的等效内阻,稳定时,磁流体发电机的电动势________,设外电路电阻为R,则R上消耗的功率________。
17.如图所示宽度为d、厚度为h的金属板放在垂直于它的磁感应强度为B的匀强磁场中,当有电流I通过金属板时,在金属板上侧面A和下侧面A′间产生电势差.
(1)金属板上侧面A电势____________下侧面电势(填高于或低于);
(2)若金属板内单位体积内自由电子数为n,则产生的电势差U=___________________.
18.如图甲所示,在平面直角坐标系中,原点O处有一粒子源,可沿y轴正方向以初速度发射质量为m、电荷量为的粒子(重力不可忽略)。在第一、二象限内存在方向平行于x轴的电场,电场强度随时间呈期性变化的图像如图乙所示,其周期,规定x轴的正方向为场强的正方向。在第三、四象限内存在垂直纸面向里的匀强磁场和平行于纸面的匀强电场,其场强为(未知),匀强磁场的磁感应强度,粒子进入磁场后做匀速圆周运动。若时刻射出的粒子第一次穿过x轴时速度方向与x轴正方向夹角为,已知重力加速度为g,不计空气阻力。求:
(1)的大小和方向;
(2)时刻射出的粒子从射出到第三次穿过x轴所用时间以及穿过的点的位置坐标。
(3)若保持,方向沿x轴的正方向不变,O点发射的粒子第n次穿过x轴的位置坐标。
19.质谱仪是一种测定带电粒子质量和分析同位素的重要工具,在科学研究中具有重要应用.如图所示是质谱仪工作原理简图,电容器两极板相距为d,两端电压为U,板间匀强磁场磁感应强度为B1 , 一束带电量均为q的正电荷粒子从图示方向射入,沿直线穿过电容器后进入另一匀强磁场B2 , 结果分别打在a、b两点,测得两点间的距离为△R,由此可知,打在两点的粒子质量差为△m=________.(粒子重力不计)
三、解答题
20.回旋加速器在科学研究中得到了广泛应用,其原理如图甲所示:D1和D2是两个中空的半圆形金属盒,置于与盒面垂直的匀强磁场中,两个D形盒接在如图乙所示的电压为U、周期为T的交流电源上,D形盒两直径之间的区域只有电场,交流电源用来提供加速电场。位于D1的圆心处的质子源A在t=0时产生的质子(初速度可以忽略)在两盒之间被电压为U的电场加速,第一次加速后进入D形盒D2,在D形盒的磁场中运动,运动半周时交流电源电压刚好改变方向对质子继续进行加速,已知质子质量为m、带电荷量为q。半圆形D形盒所在空间只有磁场,磁场的磁感应强度为B,D形盒的半径为R,当质子被加速到最大速度后,沿D形盒边缘运动半周再将它们引出,质子的重力不计,求:
(1)质子第一次被电场加速后进入磁场的轨道半径多大;
(2)质子在磁场中运动的时间。
21.如图所示的平面直角坐标系xOy,在第一象限内有平行于y轴的匀强电场,方向沿y轴负方向;在第四象限的正方形abcd区域内有匀强磁场,方向垂直于xOy平面向外,正方形边长为L,且ab边与y轴平行。一质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第四象限,又经过磁场从y轴上的某点进入第三象限,且速度与y轴负方向成45°角,不计粒子所受的重力。求:
(1)判断粒子带电的电性,并求电场强度E的大小;
(2)粒子到达a点时速度的大小和方向;
(3)abcd区域内磁场的磁感应强度B的最小值。
22.如图所示,竖直平面内建立直角坐标系xOy,y轴正向竖直向上,x轴正向水平向右,x轴在水平平面M内,在x轴上方存在竖直向下的匀强电场E1。两平行水平面M和N之间的距离为d,其间的区域存在竖直向上的匀强电场E2(E2=E1)和水平向外的匀强磁场B。带电量分别为q和-q(q>0)的小球1和2先后从y轴上距0点为h的P点以相同的初速率v0沿x轴正向水平射出,小球1从x轴上距O点为2h的A点进入MN间,恰好未从平面N离开。小球2从x轴上C点进入两平面间,最后从平面N上某点离开。设两小球质量分别为m1和m2,且qE1=2m1g,题中h、d和重力加速度g已知,其它量均未知。
(1)求两小球的初速率v。;
(2)求电场强度E2和磁感应强度B大小之比;
(3)若C点坐标为(4h,0),求m1和m2之比以及球2离开平面N时速度大小。
23.某离子实验装置如图所示,离子的运动控制在长度可调的长方体内,长方体的左右两个侧面分别放置记录板P、Q,现以长方体的一个底角O为坐标原点,建立空间直角坐标系Oxyz,MNRS是一个与x轴垂直的竖直分界面,对应的x坐标为L,分界面左侧有沿y轴正方向的匀强电场,电场强度大小为,右侧有沿y轴负方向的匀强电场和匀强磁场,离子发射器K发射出正离子(初速度大小可以忽略),经加速电压加速后正对O点进入控制区,当发射离子的质量为m、电荷量为q时,离子经过竖直分界面MNRS后,又能返回分界面,且速度方向与界面垂直,最后到达左侧记录板P,设匀强磁场的磁感应强度B的大小等于的大小,离子重力忽略不计,求:
(1)离子第一次到达分界面MNRS时的速度:
(2)竖直分界面右侧匀强电场的电场强度大小;
(3)离子到达左侧记录板P的位置与O点的距离。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【详解】
粒子先在电场中加速,根据动能定理有
在磁场中做匀速圆周运动有
解得
粒子在磁场中的周期
A. 粒子从磁场Ⅰ区域进入磁场Ⅱ区域,B减小,因为洛伦兹力不做功,所以线速度v的大小不变,r增大,由线速度、角速度的关系
可知角速度减小,故粒子自磁场Ⅰ区域进入磁场Ⅱ区域线速度大小均不变,角速度均减小,A错误;
B. 粒子从磁场Ⅰ区域进入磁场Ⅱ区域,速率不变,B变小,洛伦兹力变小,则向心加速度减小,周期变大,B错误;
CD. 粒子和质子的质量之比为
电荷量之比为
即
结合
可知无论在磁场Ⅰ区域还是在磁场Ⅱ区域中,粒子的轨迹半径均大于质子轨迹半径,C错误;
结合
可知无论在磁场Ⅰ区域还是在磁场Ⅱ区域中,粒子的周期均大于质子的周期,D正确;
故选D。
2.B
【详解】
AB.粒子无论带上何种电荷,只要以同样的速度v入射,其所受洛伦兹力和电场力始终平衡,粒子都不会发生偏转,故A错误,B正确;
C.若带电粒子的入射速度v′>v,且粒子带负电,它将一定向下偏转,故C错误;
D.若带电粒子的入射速度v′故选B。
3.D
【详解】
AB. b和c粒子沿直线运动后进入偏转磁场,b粒子打在点,c粒子打在点,由左手定则可知b粒子带负电,c粒子带正电,b和c粒子在速度选择器中沿直线运动,在速度选择器中受力平衡,则有
解得
说明在速度选择器中做直线运动的速度与粒子的比荷无关,即有
由于c粒子带正电,c粒子在速度选择器中受到的洛伦兹力向上,电场力向下,可知电场方向由上极板指向下极板,故上极板比下极板的电势高,选项AB错误;
C. 当a粒子带正电时,a粒子在速度选择器中受到的洛伦兹力向上,电场力向下,由a粒子打在速度选择器的上极板,可知
解得
当a粒子带负电时,a粒子在速度选择器中受到的洛伦兹力向下,电场力向上,由a粒子打在速度选择器的上极板,可知
解得
由于不知道a粒子在速度选择器中的具体速度大小,故a粒子可能带正电,也可能带负电,选项C错误;
D. b和c粒子在偏转磁场中,根据牛顿第二定律
解得
可知b和c粒子在偏转磁场中的轨迹半径与粒子的比荷成反比,从轨迹图可知
故有b粒子的比荷一定大于c粒子的比荷,选项D正确;
故选D。
4.C
【详解】
AB.根据左手定则,正离子受到洛伦兹力方向向上,负离子受到洛伦兹力方向向下,上电极聚集正离子,下电极聚集负离子,所以上电极电势高于下电极,电极电势高低与血液中正、负离子多少无关,故AB错误;
CD.当电场力和洛伦兹力相等时有
解得
可知,毫伏表的示数U与血液的流速成正比,与血液中正负离子的电荷量无关,故C正确,D错误。
5.C
【详解】
A.根据左手定则,施加的磁场方向为垂直纸面向里,A错误;
BC.根据动能定理
根据牛顿第二定律
解得
在图乙基础上仅提高电子的加速电压,电子的轨道半径增大,不能得到图丙所示电子束径迹;在图乙基础上仅增大磁感应强度,电子的轨道半径减小,可得到图丙所示电子束径迹,B错误,C正确;
D.若图丙中的轨迹仅仅是由于减小加速电压U而磁感应强度B不变才使得轨道半径减小,根据
图乙与图丙中的电子运动一周的时间是相等的,D错误。
故选C。
6.B
【详解】
A.为了保证粒子每次经过电场时都被加速,要求加速电压U的周期等于粒子的回旋周期,故A错误;
BC.粒子出磁场时,根据洛伦兹力提供向心力
动能为
联立解得粒子的出射动能
可见,粒子获得能量与加速的电压无关,与D形盒的半径以及磁感应强度B有关,增大磁场B和D型盒半径R,粒子获得能量增大,故C错误,B正确;
D.由于粒子最终获得的总动能不变,粒子周期不变,加速电压U越大,加速次数越少,粒子在D形盒中运动时间越短,故D错误。
故选B。
7.B
【详解】
假设粒子带正电,则所受电场力向下,由左手定则知所受洛伦兹力方向向上,由受力分析结合运动轨迹知
qvB>qE
则
v>
运动过程中洛伦兹力不做功,电场力做负功,则粒子速度减小;若粒子带负电,所受电场力向上,则由左手定则知所受洛伦兹力方向向下,由受力分析结合运动轨迹知
qvB则
v<
运动过程中洛伦兹力不做功,电场力做正功,则粒子速度增大,选项ACD错误,B正确。
故选B。
8.B
【详解】
A. 粒子在磁场中做圆周运动的周期为,由公式可看出,粒子的周期不变,粒子每次在磁场中偏转的时间等于半个周期,所以时间是不变的,故A错误;
B. 粒子每次在电场中加速,加速电压相同,根据动能定理得
每次增加的动能相同,故B正确;
CD. 当粒子最后离开D形盒时,对应的圆周运动半径为R,根据牛顿第二定律得
解得
所以动能为
与高频交流的电压无关;减小磁感应强度B,将使动能减小,故CD错误。
故选B。
9.C
【详解】
A.根据
解得
故粒子加速后的最大速度与D型金属盒的半径有关,故A错误;
B.根据
联立解得
最大动能与半径和磁感应强度有关与加速电压无关,故B错误;
CD.根据
可知高频电源频率由粒子的质量、电量和磁感应强度决定,故C正确,D错误。
故选C。
10.B
【详解】
AB.第1个图:由竖直上抛运动的最大高度公式得
ha=
第3个图:当加上电场时,由运动的分解可知,在竖直方向上有
v02=2ghc
所以
ha=hc
而第2个图:洛伦兹力改变速度的方向,当小球在磁场中运动到最高点时,小球应有水平速度,设此时的球的动能为Ek,则由能量守恒得
mghb+Ek=mv02
又由于
mv02=mgha
所以
ha>hb
则它们上升的最大高度关系为
hb选项A错误,B正确;
C.小球a的机械能守恒,因洛伦兹力不做功,小球b到达最大高度时,机械能也守恒,而电场力做正功,则c小球机械能最大,则选项C错误;
D.到达最大高度时,a小球速度为零,则动能最小,故D错误。
故选B。
11.C
【详解】
A.小球从M到N,在竖直方向上发生了偏转,所以受到的竖直向下的洛伦兹力、竖直向下的重力和竖直向上的电场力的合力不为零,并且速度方向变化,则洛伦兹力方向变化,所以合力方向变化,故不可能做匀变速运动,一定做变加速运动,A错误;
B.小球从M到N过程中电场力的做负功,电势能必然增加,B错误;
C.若电场力和重力等大反向,则运动过程中电场力和重力做功之和为零,而洛伦兹力不做功,所以小球的动能可能不变,C正确;
D.沿电场方向有位移,电场力一定做负功,机械能转化为电势能,故小球的机械能减小不可能增加,D错误。
故选C。
12.D
【详解】
A.仅减小小球从P点进入的速度大小,由于小球的速度会变,合外力会变,则小球不会做匀变速曲线运动,A错误;
BC.仅减小小球从P点进入的速度大小时,洛伦兹力减小,则电场力和重力不变,小球将向上偏转,电场力和重力的合力向上,且它们的合力对小球做正功,小球动能增大,小球的机械能增大,电场力对小球做正功,电势能减小,重力对小球做负功,重力势能增大,BC错误;
D.由于电势能减小,重力势能增大,动能增大,减小电势能转化为动能和重力势能,故小球的电势能和动能之和减小,D正确。
故选D。
13.D
【详解】
A.污水流速为v,则当M、N间电压为U时,有
解得
流量为
解得
故A错误;
B.由左手定则可知,正离子受洛伦兹力向上,负离子受洛伦兹力向下,使M板带正电,N板带负电,则金属板M的电势高于金属板N的电势,故B错误;
C.金属板M、N间电压为U,由
得
电压U与污水粒子的浓度无关,故C错误;
D.设左右两侧管口压强差为 ,污水匀速流动,由平衡关系得
将代入上式得
故D正确。
故选D。
14.C
【详解】
A.所加电压规律不变,则粒子周期
T1=T2
由
T=
即
A错误;
B.由
得
v=
知r越大,v越大,则r的最大值为回旋加速器的半径R,
vmax=
Ekmax1:Ekmax2=∶
又由
得
=
B错误;
C.加速次数N满足
NqU=Ekmax
所以
N=
又由
=
所以
==
选项C正确;
D.加速周期
T1=T2
加速次数
=
加速时间
t=·T
得
===
选项D错误。
故选C。
15.A
【详解】
A.因为洛伦兹力和大圆环的支持力对小圆环均不做功,且大圆环光滑,所以根据机械能守恒定律可知小圆环可以运动到N点,且小圆环在MD弧上和ND弧上等高位置速度大小相同,根据对称性可知小圆环在MD弧上运动时所受平均合外力与在ND弧上所受平均合外力相同,根据动量定理可知小环由M滑到D点所用时间与由D滑到N点所用时间相同,故A正确;
B.根据机械能守恒定律有
解得
故B错误;
CD.设小环滑到D点时所受轨道的弹力大小为N,根据牛顿第二定律有
解得
根据牛顿第三定律可知小环滑到D点时对圆环轨道的弹力一定大于mg,并且如果改变圆环的半径,小圆环从M滑到D点时在D点对圆环轨道的弹力随圆环半径的增大而增大,故CD错误。
故选A。
16.
【详解】
[1]设当A、B电极两端电压为U时磁流体发电机稳定发电,此时有
由匀强电场的电场强度与电势差的关系
得磁流体发电机的电动势
[2]当外电路电阻为R,无电源内阻时
17. 低于
【详解】
(1)[1]根据左手定则,电子向上偏,所以上侧面得到电子带负电,下侧面失去电子带正电,则金属板上侧面A电势低于下侧面的电势.
(2)[2]电子最终达到平衡,有
则
U=vBh
电流的微观表达式
I=nevS=nevhd
则
代入得
【点睛】
金属中移动的是自由电子,根据左手定则,判断出电子的偏转方向,从而得出电势的高低.最终电子受电场力和洛伦兹力平衡,根据平衡和电流的微观表达式求出电势差的大小.
18.(1),方向竖直向上;(2),;(3)
【详解】
(1)要使带正电粒子做匀速圆周运动,则有
解得
方向竖直向上;
(2)设场强为时加速度为,场强为时加速度为,粒子第一次穿过x轴的水平速度为有
所用时间
则有
解得
时刻射入的粒子第一次穿过x轴的水平速度
粒子进入磁场后做匀速圆周运动,则有
解得
所以
所以位置坐标为;
(3)设粒子进入磁场时与水平方向夹角为,则进入磁场时的速度
所以此时圆周运动半径
入射点和出射点之间的距离
由此可知每次入射点和出射点之间的距离为一个定值
且由分析可得,在电场中的水平方向的运动合起来可看作一匀加速直线运动,所以
①若n为奇数,有
②若n为偶数,有
19.
【详解】
电容器中有正交的电场与磁场,带电粒子匀速通过,受力平衡
满足速度选择题的原理:,
而匀强电场
解得匀速的速度,
进入磁场B2后,洛伦兹力提供向心力:
解得:
同位素的电量相等,质量不等,有
故解得质量差为
【点睛】
解决本题的关键知道从速度选择器进入偏转磁场,速度相同.以及知道在偏转磁场中的半径与电荷的比荷有关,同位素,电量相同,质量不同,偏转的半径就不同.
20.(1);(2)
【详解】
(1)质子在加速电场中第一次被加速,根据动能定理
qU=m
在磁场中洛伦兹力提供向心力,根据牛顿第二定律,有
qv1B=
解得
r=
(2)设质子被加速n次后达到最大速度v,由动能定理
nqU=mv2
洛伦兹力提供质子做圆周运动的向心力,有
qvB=m
周期
T=
则质子在磁场中运动的时间
t=n
联立可解得
21.(1)正电;;(2),方向指向第Ⅳ象限与x轴正方向成45°角;(3)
【详解】
(1)粒子垂直于电场方向进入电场后沿电场线方向偏转,故粒子带正电;
设粒子在电场中运动的时间为t,粒子在电场中做类平抛运动,则有
联立以上各式可得
(2)粒子到达a点时沿y轴方向的分速度
所以,粒子进入磁场的速度为
方向指向第Ⅳ象限与x轴正方向成45°角。
(3)粒子在磁场中运动时,有
粒子又经过磁场从y轴上的某点进入第三象限,且速度与y轴负方向成45°角,故粒子在磁场中的偏转角为,分析得:当粒子从b点射出时,磁场的磁感应强度为最小值,此时有
所以
22.(1);(2);(3),
【详解】
(1)小球1在x轴上方做类平抛运动
解得
(2)因为
则
所以小球1在MN间做匀速圆周运动。由题意小球1恰好未从下边界平面N离开知其轨迹应与平面N相切,如图所示,
由几何关系可知
设小球1刚进入MN间时速度偏转角为θ1,
由
又
得
(3)小球2在x轴上方做类平抛运动:
结合(1)问中4个式子可得
小球2从P点到离开平面N全过程由动能定理得
解得
23.(1);(2);(3)
【详解】
(1)在加速电场中,由动能定理得
在偏转电场中离子做匀变速曲线运动
x轴方向有
y轴方向有
,
解得
离子到达分界面MNRS时的速度为
故离子第一次到达分界面MNRS时速度为。
(2)进入磁场后:xOz平面内在洛伦兹力作用下做匀速圆周运动,yOz平面内在电场力作用下做匀减速运动,当速度减到零时到达分界面,此时恰好完成半个圆周运动
y轴方向有
,
xOz平面内,有
,,
解得
故竖直分界面右侧匀强电场的电场强度大小为。
(3)离子第一次到达分界面时,沿y轴方向位移,有
在分界面右侧y轴方向在匀强电场作用下做匀减速运动,当速度减到零时到达分界面,此时y轴方向位移为
再次进入分界面左侧做匀变速曲线运动,到达记录板P时,y轴方向位移
整个过程中y轴方向总位移为
此过程中,x轴方向位移为
到达记录板P的位置与O点距离为
解得
故离子到达左侧记录板P的位置与O点的距离为。
答案第1页,共2页
答案第1页,共2页
试卷副标题
考试范围:xxx;考试时间:100分钟;命题人:xxx
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
1.如图所示,初速度为零的粒子和质子分别经过相同的加速电场后,沿垂直磁感应强度方向进入匀强磁场Ⅰ区域,接着进入匀强磁场Ⅱ区域。已知磁场Ⅰ、Ⅱ的磁感应强度大小分别为、,且,下列说法正确的是( )
A.粒子自磁场Ⅰ区域进入磁场Ⅱ区域线速度大小均减小,角速度均减小
B.粒子自磁场Ⅰ区域进入磁场Ⅱ区域向心加速度大小均变小,周期均变小
C.无论在磁场Ⅰ区域还是在磁场Ⅱ区域中,粒子的轨迹半径均小于质子轨迹半径
D.无论在磁场Ⅰ区域还是在磁场Ⅱ区域中,粒子的周期均大于质子的周期
2.如图所示,M、N为一对水平放置的平行金属板,一带电粒子以平行于金属板方向的速度v穿过平行金属板。若在两板间存在互相垂直的匀强电场和匀强磁场,可使带电粒子的运动不发生偏转,做匀速直线运动。不计粒子所受的重力,则以下叙述正确的是( )
A.若改变粒子的电性,即使它以同样速度v射入该区域,其运动方向也一定会发生偏转
B.粒子无论带上何种电荷,只要以同样的速度v入射,都不会发生偏转
C.若带电粒子的入射速度v′>v,它将一定向上偏转
D.若带电粒子的入射速度v′
A.上极板比下极板的电势低 B.一定有
C.a、b粒子一定都带负电 D.b粒子的比荷一定大于c粒子的比荷
4.霍尔效应可用来测量血流速度,其原理如图所示。在动脉血管上下两侧安装电极,左右两侧加以磁场,毫伏表测出上下两极的电压为U。则( )
A.上电极电势一定低于下电极
B.若血液中负离子较多时,上电极电势低于下电极
C.毫伏表的示数U与血液的流速成正比
D.毫伏表的示数U与血液中正负离子的电荷量成正比
5.如图所示,用洛伦兹力演示仪研究带电粒子在匀强磁场中的运动,以虚线表示电极K释放出来的电子束的径迹。在施加磁场之前,电子经加速后沿直线运动,如图甲所示;施加磁场后电子束的径迹,如图乙所示;再调节演示仪可得到图丙所示的电子束径迹。下列说法正确的是( )
A.施加的磁场方向为垂直纸面向外
B.在图乙基础上仅提高电子的加速电压,可得到图丙所示电子束径迹
C.在图乙基础上仅增大磁感应强度,可得到图丙所示电子束径迹
D.图乙与图丙中电子运动一周的时间不相等
6.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狹缝很小,带电粒子穿过的区时间可忽略不计,磁感应强度为B的匀强磁场与盒面垂直,A处粒子源产生的粒子质量为m、电荷量为,在加速器中被加速,加速电压为U,加速过程中不考虑相对论效应和重力影响,则( )
A.加速器加速电压U的周期等于粒子的回旋周期的两倍
B.增大加速电压U,出射粒子动能不变
C.增大磁感应强度B和D形盒半径R,粒子获得动能可能减小
D.粒子在D形盒中运动时间与加速电压U无关
7.如图所示是一速度选择器,当粒子速度满足v0=时,粒子沿图中虚线水平射出;若某一粒子以速度v射入该速度选择器后,运动轨迹为图中实线,则关于该粒子的说法正确的是( )
A.粒子射入的速度一定是v>
B.粒子射入的速度可能是v<
C.粒子射出时的速度一定大于射入速度
D.粒子射出时的速度一定小于射入速度
8.回旋加速器主体部分是两个D形金属盒。两金属盒处在垂直于盒底的匀强磁场中,并分别与高频交流电源两极相连接,从而使粒子每次经过两盒间的狭缝时都得到加速,如图所示。在粒子质量不变和D形盒外径R固定的情况下,下列说法正确的是( )
A.粒子每次在磁场中偏转的时间随着加速次数的增加而增大
B.粒子在电场中加速时每次获得的能量相同
C.增大高频交流的电压,则可以增大粒子最后偏转出D形盒时的动能
D.将磁感应强度B减小,则可以增大粒子最后偏转出D形盒时的动能
9.回旋加速器是用来加速带电粒子使它获得很大动能的装置,其核心部分是两个D型金属盒,置于匀强磁场中,两盒分别与高频电源相连。下列说法正确的是( )
A.粒子被加速后的最大速度与D型金属盒的半径无关
B.粒子被加速后的最大动能随高频电源的加速电压的增大而增大
C.高频电源频率由粒子的质量、电量和磁感应强度决定
D.高频电源频率与粒子的质量、电量和磁感应强度无关
10.如图所示带电小球a以一定的初速度v0竖直向上抛出,能够达到的最大高度为ha;带电小球b在水平方向的匀强磁场以相同的初速度v0竖直向上抛出,上升的最大高度为hb;带电小球c在水平方向的匀强电场以相同的初速度v0竖直向上抛出,上升的最大高度为hc,不计空气阻力,三个小球的质量相等,则正确的是( )
A.它们上升的最大高度关系为ha=hb=hc
B.它们上升的最大高度关系为hb
D.到达最大高度时,b小球动能最小
11.如图所示,空间某处存在竖直向下的匀强电场和垂直纸面向里的匀强磁场,一个带负电的金属小球从M点水平射入场区,经一段时间运动到N点,关于小球由M到N的运动,下列说法正确的是( )
A.小球可能做匀变速运动 B.小球的电势能可能减少
C.小球动能可能不变 D.小球机械能可能增加
12.如图所示,两竖直平行虚线边界内,匀强电场方向竖直(平行纸面)向下,匀强磁场方向垂直纸面向里,一带负电小球从P点以某一速度垂直边界进入,恰好沿水平方向做直线运动,若仅减小小球从P点进入的速度大小,则在小球进入的一小段时间内( )
A.小球做匀变速曲线运动 B.小球的电势能增大
C.小球的机械能减小 D.小球的电势能和动能之和减小
13.为了测量化工厂的污水排放量,技术人员在排污管末端安装了流量计(流量Q为单位时间内流过某截面流体的体积)。如图所示,长方体绝缘管道的长、宽、高分别为a、b、c,左、右两端开口,所在空间有垂直于前后面向里、磁感应强度大小为B的匀强磁场,在上、下两个面的内侧固定有金属板M、N,含有大量的正、负离子的污水充满管道,从左向右匀速流动,测得M、N间电压为U。由于污水流过管道时受到阻力f的作用,左、右两侧管口需要维持一定的压强差。已知沿流速方向长度为L、流速为v的污水,受到的阻力(k为比例系数)。下列说法正确的是( )
A.污水的流量
B.金属板的电势低于金属板的电势
C.电压与污水中的离子浓度有关
D.左、右两侧管口的压强差为
14.图甲是回旋加速器的示意图,粒子出口处如图所示.图乙是回旋加速器所用的交变电压随时间的变化规律。某物理学习小组在学习了回旋加速器原理之后,想利用同一回旋加速器分别加速两种带正电的粒子,所带电荷量分别为q1、q2,质量分别为m1、m2。保持交变电压随时间变化的规律不变,需要调整所加磁场的磁感应强度的大小,则( )
A.所加磁场的磁感应强度大小之比为
B.粒子获得的最大动能之比为
C.粒子的加速次数之比为
D.粒子在回旋加速器中的运动时间之比为
15.如图所示,MDN为绝缘材料制成的半径为R的光滑竖直半圆环,置于磁感应强度为B,方向垂直纸面向外的匀强磁场中,一质量为m,带正电可看成质点的小圆环套在大圆环上,从M点无初速下落,D为圆环最低点,N点与M点等高,小圆环在运动的过程中,下列说法中正确的是( )
A.小环由M滑到D点所用时间与由D滑到N点所用时间相同
B.小环滑到D点时速率满足
C.小环滑到D点时对圆环轨道的弹力一定小于mg
D.如果改变圆环的半径,小圆环从M滑到D点时在D点对圆环轨道的弹力随圆环半径的增大而减小
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
16.磁流体发电是一项新兴技术,它可以把气体的内能直接转化为电能。下图是磁流体发电机的装置:A、B组成一对平行电极,两极间距为d,内有磁感应强度为B的匀强磁场,现持续将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而整体呈中性)垂直喷射入磁场,每个离子的速度为v,电荷量大小为q,忽略两极之间的等效内阻,稳定时,磁流体发电机的电动势________,设外电路电阻为R,则R上消耗的功率________。
17.如图所示宽度为d、厚度为h的金属板放在垂直于它的磁感应强度为B的匀强磁场中,当有电流I通过金属板时,在金属板上侧面A和下侧面A′间产生电势差.
(1)金属板上侧面A电势____________下侧面电势(填高于或低于);
(2)若金属板内单位体积内自由电子数为n,则产生的电势差U=___________________.
18.如图甲所示,在平面直角坐标系中,原点O处有一粒子源,可沿y轴正方向以初速度发射质量为m、电荷量为的粒子(重力不可忽略)。在第一、二象限内存在方向平行于x轴的电场,电场强度随时间呈期性变化的图像如图乙所示,其周期,规定x轴的正方向为场强的正方向。在第三、四象限内存在垂直纸面向里的匀强磁场和平行于纸面的匀强电场,其场强为(未知),匀强磁场的磁感应强度,粒子进入磁场后做匀速圆周运动。若时刻射出的粒子第一次穿过x轴时速度方向与x轴正方向夹角为,已知重力加速度为g,不计空气阻力。求:
(1)的大小和方向;
(2)时刻射出的粒子从射出到第三次穿过x轴所用时间以及穿过的点的位置坐标。
(3)若保持,方向沿x轴的正方向不变,O点发射的粒子第n次穿过x轴的位置坐标。
19.质谱仪是一种测定带电粒子质量和分析同位素的重要工具,在科学研究中具有重要应用.如图所示是质谱仪工作原理简图,电容器两极板相距为d,两端电压为U,板间匀强磁场磁感应强度为B1 , 一束带电量均为q的正电荷粒子从图示方向射入,沿直线穿过电容器后进入另一匀强磁场B2 , 结果分别打在a、b两点,测得两点间的距离为△R,由此可知,打在两点的粒子质量差为△m=________.(粒子重力不计)
三、解答题
20.回旋加速器在科学研究中得到了广泛应用,其原理如图甲所示:D1和D2是两个中空的半圆形金属盒,置于与盒面垂直的匀强磁场中,两个D形盒接在如图乙所示的电压为U、周期为T的交流电源上,D形盒两直径之间的区域只有电场,交流电源用来提供加速电场。位于D1的圆心处的质子源A在t=0时产生的质子(初速度可以忽略)在两盒之间被电压为U的电场加速,第一次加速后进入D形盒D2,在D形盒的磁场中运动,运动半周时交流电源电压刚好改变方向对质子继续进行加速,已知质子质量为m、带电荷量为q。半圆形D形盒所在空间只有磁场,磁场的磁感应强度为B,D形盒的半径为R,当质子被加速到最大速度后,沿D形盒边缘运动半周再将它们引出,质子的重力不计,求:
(1)质子第一次被电场加速后进入磁场的轨道半径多大;
(2)质子在磁场中运动的时间。
21.如图所示的平面直角坐标系xOy,在第一象限内有平行于y轴的匀强电场,方向沿y轴负方向;在第四象限的正方形abcd区域内有匀强磁场,方向垂直于xOy平面向外,正方形边长为L,且ab边与y轴平行。一质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第四象限,又经过磁场从y轴上的某点进入第三象限,且速度与y轴负方向成45°角,不计粒子所受的重力。求:
(1)判断粒子带电的电性,并求电场强度E的大小;
(2)粒子到达a点时速度的大小和方向;
(3)abcd区域内磁场的磁感应强度B的最小值。
22.如图所示,竖直平面内建立直角坐标系xOy,y轴正向竖直向上,x轴正向水平向右,x轴在水平平面M内,在x轴上方存在竖直向下的匀强电场E1。两平行水平面M和N之间的距离为d,其间的区域存在竖直向上的匀强电场E2(E2=E1)和水平向外的匀强磁场B。带电量分别为q和-q(q>0)的小球1和2先后从y轴上距0点为h的P点以相同的初速率v0沿x轴正向水平射出,小球1从x轴上距O点为2h的A点进入MN间,恰好未从平面N离开。小球2从x轴上C点进入两平面间,最后从平面N上某点离开。设两小球质量分别为m1和m2,且qE1=2m1g,题中h、d和重力加速度g已知,其它量均未知。
(1)求两小球的初速率v。;
(2)求电场强度E2和磁感应强度B大小之比;
(3)若C点坐标为(4h,0),求m1和m2之比以及球2离开平面N时速度大小。
23.某离子实验装置如图所示,离子的运动控制在长度可调的长方体内,长方体的左右两个侧面分别放置记录板P、Q,现以长方体的一个底角O为坐标原点,建立空间直角坐标系Oxyz,MNRS是一个与x轴垂直的竖直分界面,对应的x坐标为L,分界面左侧有沿y轴正方向的匀强电场,电场强度大小为,右侧有沿y轴负方向的匀强电场和匀强磁场,离子发射器K发射出正离子(初速度大小可以忽略),经加速电压加速后正对O点进入控制区,当发射离子的质量为m、电荷量为q时,离子经过竖直分界面MNRS后,又能返回分界面,且速度方向与界面垂直,最后到达左侧记录板P,设匀强磁场的磁感应强度B的大小等于的大小,离子重力忽略不计,求:
(1)离子第一次到达分界面MNRS时的速度:
(2)竖直分界面右侧匀强电场的电场强度大小;
(3)离子到达左侧记录板P的位置与O点的距离。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【详解】
粒子先在电场中加速,根据动能定理有
在磁场中做匀速圆周运动有
解得
粒子在磁场中的周期
A. 粒子从磁场Ⅰ区域进入磁场Ⅱ区域,B减小,因为洛伦兹力不做功,所以线速度v的大小不变,r增大,由线速度、角速度的关系
可知角速度减小,故粒子自磁场Ⅰ区域进入磁场Ⅱ区域线速度大小均不变,角速度均减小,A错误;
B. 粒子从磁场Ⅰ区域进入磁场Ⅱ区域,速率不变,B变小,洛伦兹力变小,则向心加速度减小,周期变大,B错误;
CD. 粒子和质子的质量之比为
电荷量之比为
即
结合
可知无论在磁场Ⅰ区域还是在磁场Ⅱ区域中,粒子的轨迹半径均大于质子轨迹半径,C错误;
结合
可知无论在磁场Ⅰ区域还是在磁场Ⅱ区域中,粒子的周期均大于质子的周期,D正确;
故选D。
2.B
【详解】
AB.粒子无论带上何种电荷,只要以同样的速度v入射,其所受洛伦兹力和电场力始终平衡,粒子都不会发生偏转,故A错误,B正确;
C.若带电粒子的入射速度v′>v,且粒子带负电,它将一定向下偏转,故C错误;
D.若带电粒子的入射速度v′
3.D
【详解】
AB. b和c粒子沿直线运动后进入偏转磁场,b粒子打在点,c粒子打在点,由左手定则可知b粒子带负电,c粒子带正电,b和c粒子在速度选择器中沿直线运动,在速度选择器中受力平衡,则有
解得
说明在速度选择器中做直线运动的速度与粒子的比荷无关,即有
由于c粒子带正电,c粒子在速度选择器中受到的洛伦兹力向上,电场力向下,可知电场方向由上极板指向下极板,故上极板比下极板的电势高,选项AB错误;
C. 当a粒子带正电时,a粒子在速度选择器中受到的洛伦兹力向上,电场力向下,由a粒子打在速度选择器的上极板,可知
解得
当a粒子带负电时,a粒子在速度选择器中受到的洛伦兹力向下,电场力向上,由a粒子打在速度选择器的上极板,可知
解得
由于不知道a粒子在速度选择器中的具体速度大小,故a粒子可能带正电,也可能带负电,选项C错误;
D. b和c粒子在偏转磁场中,根据牛顿第二定律
解得
可知b和c粒子在偏转磁场中的轨迹半径与粒子的比荷成反比,从轨迹图可知
故有b粒子的比荷一定大于c粒子的比荷,选项D正确;
故选D。
4.C
【详解】
AB.根据左手定则,正离子受到洛伦兹力方向向上,负离子受到洛伦兹力方向向下,上电极聚集正离子,下电极聚集负离子,所以上电极电势高于下电极,电极电势高低与血液中正、负离子多少无关,故AB错误;
CD.当电场力和洛伦兹力相等时有
解得
可知,毫伏表的示数U与血液的流速成正比,与血液中正负离子的电荷量无关,故C正确,D错误。
5.C
【详解】
A.根据左手定则,施加的磁场方向为垂直纸面向里,A错误;
BC.根据动能定理
根据牛顿第二定律
解得
在图乙基础上仅提高电子的加速电压,电子的轨道半径增大,不能得到图丙所示电子束径迹;在图乙基础上仅增大磁感应强度,电子的轨道半径减小,可得到图丙所示电子束径迹,B错误,C正确;
D.若图丙中的轨迹仅仅是由于减小加速电压U而磁感应强度B不变才使得轨道半径减小,根据
图乙与图丙中的电子运动一周的时间是相等的,D错误。
故选C。
6.B
【详解】
A.为了保证粒子每次经过电场时都被加速,要求加速电压U的周期等于粒子的回旋周期,故A错误;
BC.粒子出磁场时,根据洛伦兹力提供向心力
动能为
联立解得粒子的出射动能
可见,粒子获得能量与加速的电压无关,与D形盒的半径以及磁感应强度B有关,增大磁场B和D型盒半径R,粒子获得能量增大,故C错误,B正确;
D.由于粒子最终获得的总动能不变,粒子周期不变,加速电压U越大,加速次数越少,粒子在D形盒中运动时间越短,故D错误。
故选B。
7.B
【详解】
假设粒子带正电,则所受电场力向下,由左手定则知所受洛伦兹力方向向上,由受力分析结合运动轨迹知
qvB>qE
则
v>
运动过程中洛伦兹力不做功,电场力做负功,则粒子速度减小;若粒子带负电,所受电场力向上,则由左手定则知所受洛伦兹力方向向下,由受力分析结合运动轨迹知
qvB
v<
运动过程中洛伦兹力不做功,电场力做正功,则粒子速度增大,选项ACD错误,B正确。
故选B。
8.B
【详解】
A. 粒子在磁场中做圆周运动的周期为,由公式可看出,粒子的周期不变,粒子每次在磁场中偏转的时间等于半个周期,所以时间是不变的,故A错误;
B. 粒子每次在电场中加速,加速电压相同,根据动能定理得
每次增加的动能相同,故B正确;
CD. 当粒子最后离开D形盒时,对应的圆周运动半径为R,根据牛顿第二定律得
解得
所以动能为
与高频交流的电压无关;减小磁感应强度B,将使动能减小,故CD错误。
故选B。
9.C
【详解】
A.根据
解得
故粒子加速后的最大速度与D型金属盒的半径有关,故A错误;
B.根据
联立解得
最大动能与半径和磁感应强度有关与加速电压无关,故B错误;
CD.根据
可知高频电源频率由粒子的质量、电量和磁感应强度决定,故C正确,D错误。
故选C。
10.B
【详解】
AB.第1个图:由竖直上抛运动的最大高度公式得
ha=
第3个图:当加上电场时,由运动的分解可知,在竖直方向上有
v02=2ghc
所以
ha=hc
而第2个图:洛伦兹力改变速度的方向,当小球在磁场中运动到最高点时,小球应有水平速度,设此时的球的动能为Ek,则由能量守恒得
mghb+Ek=mv02
又由于
mv02=mgha
所以
ha>hb
则它们上升的最大高度关系为
hb
C.小球a的机械能守恒,因洛伦兹力不做功,小球b到达最大高度时,机械能也守恒,而电场力做正功,则c小球机械能最大,则选项C错误;
D.到达最大高度时,a小球速度为零,则动能最小,故D错误。
故选B。
11.C
【详解】
A.小球从M到N,在竖直方向上发生了偏转,所以受到的竖直向下的洛伦兹力、竖直向下的重力和竖直向上的电场力的合力不为零,并且速度方向变化,则洛伦兹力方向变化,所以合力方向变化,故不可能做匀变速运动,一定做变加速运动,A错误;
B.小球从M到N过程中电场力的做负功,电势能必然增加,B错误;
C.若电场力和重力等大反向,则运动过程中电场力和重力做功之和为零,而洛伦兹力不做功,所以小球的动能可能不变,C正确;
D.沿电场方向有位移,电场力一定做负功,机械能转化为电势能,故小球的机械能减小不可能增加,D错误。
故选C。
12.D
【详解】
A.仅减小小球从P点进入的速度大小,由于小球的速度会变,合外力会变,则小球不会做匀变速曲线运动,A错误;
BC.仅减小小球从P点进入的速度大小时,洛伦兹力减小,则电场力和重力不变,小球将向上偏转,电场力和重力的合力向上,且它们的合力对小球做正功,小球动能增大,小球的机械能增大,电场力对小球做正功,电势能减小,重力对小球做负功,重力势能增大,BC错误;
D.由于电势能减小,重力势能增大,动能增大,减小电势能转化为动能和重力势能,故小球的电势能和动能之和减小,D正确。
故选D。
13.D
【详解】
A.污水流速为v,则当M、N间电压为U时,有
解得
流量为
解得
故A错误;
B.由左手定则可知,正离子受洛伦兹力向上,负离子受洛伦兹力向下,使M板带正电,N板带负电,则金属板M的电势高于金属板N的电势,故B错误;
C.金属板M、N间电压为U,由
得
电压U与污水粒子的浓度无关,故C错误;
D.设左右两侧管口压强差为 ,污水匀速流动,由平衡关系得
将代入上式得
故D正确。
故选D。
14.C
【详解】
A.所加电压规律不变,则粒子周期
T1=T2
由
T=
即
A错误;
B.由
得
v=
知r越大,v越大,则r的最大值为回旋加速器的半径R,
vmax=
Ekmax1:Ekmax2=∶
又由
得
=
B错误;
C.加速次数N满足
NqU=Ekmax
所以
N=
又由
=
所以
==
选项C正确;
D.加速周期
T1=T2
加速次数
=
加速时间
t=·T
得
===
选项D错误。
故选C。
15.A
【详解】
A.因为洛伦兹力和大圆环的支持力对小圆环均不做功,且大圆环光滑,所以根据机械能守恒定律可知小圆环可以运动到N点,且小圆环在MD弧上和ND弧上等高位置速度大小相同,根据对称性可知小圆环在MD弧上运动时所受平均合外力与在ND弧上所受平均合外力相同,根据动量定理可知小环由M滑到D点所用时间与由D滑到N点所用时间相同,故A正确;
B.根据机械能守恒定律有
解得
故B错误;
CD.设小环滑到D点时所受轨道的弹力大小为N,根据牛顿第二定律有
解得
根据牛顿第三定律可知小环滑到D点时对圆环轨道的弹力一定大于mg,并且如果改变圆环的半径,小圆环从M滑到D点时在D点对圆环轨道的弹力随圆环半径的增大而增大,故CD错误。
故选A。
16.
【详解】
[1]设当A、B电极两端电压为U时磁流体发电机稳定发电,此时有
由匀强电场的电场强度与电势差的关系
得磁流体发电机的电动势
[2]当外电路电阻为R,无电源内阻时
17. 低于
【详解】
(1)[1]根据左手定则,电子向上偏,所以上侧面得到电子带负电,下侧面失去电子带正电,则金属板上侧面A电势低于下侧面的电势.
(2)[2]电子最终达到平衡,有
则
U=vBh
电流的微观表达式
I=nevS=nevhd
则
代入得
【点睛】
金属中移动的是自由电子,根据左手定则,判断出电子的偏转方向,从而得出电势的高低.最终电子受电场力和洛伦兹力平衡,根据平衡和电流的微观表达式求出电势差的大小.
18.(1),方向竖直向上;(2),;(3)
【详解】
(1)要使带正电粒子做匀速圆周运动,则有
解得
方向竖直向上;
(2)设场强为时加速度为,场强为时加速度为,粒子第一次穿过x轴的水平速度为有
所用时间
则有
解得
时刻射入的粒子第一次穿过x轴的水平速度
粒子进入磁场后做匀速圆周运动,则有
解得
所以
所以位置坐标为;
(3)设粒子进入磁场时与水平方向夹角为,则进入磁场时的速度
所以此时圆周运动半径
入射点和出射点之间的距离
由此可知每次入射点和出射点之间的距离为一个定值
且由分析可得,在电场中的水平方向的运动合起来可看作一匀加速直线运动,所以
①若n为奇数,有
②若n为偶数,有
19.
【详解】
电容器中有正交的电场与磁场,带电粒子匀速通过,受力平衡
满足速度选择题的原理:,
而匀强电场
解得匀速的速度,
进入磁场B2后,洛伦兹力提供向心力:
解得:
同位素的电量相等,质量不等,有
故解得质量差为
【点睛】
解决本题的关键知道从速度选择器进入偏转磁场,速度相同.以及知道在偏转磁场中的半径与电荷的比荷有关,同位素,电量相同,质量不同,偏转的半径就不同.
20.(1);(2)
【详解】
(1)质子在加速电场中第一次被加速,根据动能定理
qU=m
在磁场中洛伦兹力提供向心力,根据牛顿第二定律,有
qv1B=
解得
r=
(2)设质子被加速n次后达到最大速度v,由动能定理
nqU=mv2
洛伦兹力提供质子做圆周运动的向心力,有
qvB=m
周期
T=
则质子在磁场中运动的时间
t=n
联立可解得
21.(1)正电;;(2),方向指向第Ⅳ象限与x轴正方向成45°角;(3)
【详解】
(1)粒子垂直于电场方向进入电场后沿电场线方向偏转,故粒子带正电;
设粒子在电场中运动的时间为t,粒子在电场中做类平抛运动,则有
联立以上各式可得
(2)粒子到达a点时沿y轴方向的分速度
所以,粒子进入磁场的速度为
方向指向第Ⅳ象限与x轴正方向成45°角。
(3)粒子在磁场中运动时,有
粒子又经过磁场从y轴上的某点进入第三象限,且速度与y轴负方向成45°角,故粒子在磁场中的偏转角为,分析得:当粒子从b点射出时,磁场的磁感应强度为最小值,此时有
所以
22.(1);(2);(3),
【详解】
(1)小球1在x轴上方做类平抛运动
解得
(2)因为
则
所以小球1在MN间做匀速圆周运动。由题意小球1恰好未从下边界平面N离开知其轨迹应与平面N相切,如图所示,
由几何关系可知
设小球1刚进入MN间时速度偏转角为θ1,
由
又
得
(3)小球2在x轴上方做类平抛运动:
结合(1)问中4个式子可得
小球2从P点到离开平面N全过程由动能定理得
解得
23.(1);(2);(3)
【详解】
(1)在加速电场中,由动能定理得
在偏转电场中离子做匀变速曲线运动
x轴方向有
y轴方向有
,
解得
离子到达分界面MNRS时的速度为
故离子第一次到达分界面MNRS时速度为。
(2)进入磁场后:xOz平面内在洛伦兹力作用下做匀速圆周运动,yOz平面内在电场力作用下做匀减速运动,当速度减到零时到达分界面,此时恰好完成半个圆周运动
y轴方向有
,
xOz平面内,有
,,
解得
故竖直分界面右侧匀强电场的电场强度大小为。
(3)离子第一次到达分界面时,沿y轴方向位移,有
在分界面右侧y轴方向在匀强电场作用下做匀减速运动,当速度减到零时到达分界面,此时y轴方向位移为
再次进入分界面左侧做匀变速曲线运动,到达记录板P时,y轴方向位移
整个过程中y轴方向总位移为
此过程中,x轴方向位移为
到达记录板P的位置与O点距离为
解得
故离子到达左侧记录板P的位置与O点的距离为。
答案第1页,共2页
答案第1页,共2页
