苏科版数学八年级下册第9章中心对称图形-平行四边形单元检测(基础卷)(word版含答案)
文档属性
| 名称 | 苏科版数学八年级下册第9章中心对称图形-平行四边形单元检测(基础卷)(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 294.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-09 04:24:10 | ||
图片预览




文档简介
第9章中心对称图形-平行四边形
一、单选题
1.下列旋转中,旋转中心为点A的是( )
A. B.
C. D.
2.已知四边形ABCD是平行四边形,下列说法正确的有( )
①当AB=BC时,它是矩形
②AC⊥BD时,它是菱形
③当∠ABC=90°时,它是菱形
④当AC=BD时,它是正方形
A.①② B.② C.②④ D.③④
3.如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长( )
A. B.2﹣2 C.2﹣ D.2
4.以下四张扑克牌的图案,中心对称图形是( )
A. B. C. D.
5.如图,在平行四边形ABCD中,过对角线AC与BD的交点O作AC的垂线交AD于点E,连接CE,若AB=4,BC=6,则△CDE的周长是( )
A.10 B.5 C.8 D.6
6.在 ABCD中,若∠BAD与∠CDA的角平分线交于点E,则△AED的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
7.如图,,,分别是边,,上的中点,若阴影的面积为,则的面积是( )
A. B. C. D.
8.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.2 C.3 D.4
9.如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
A.9 B.18 C.36 D.48
10.如图,在中,,点分别是边上的动点,连接,点分别为的中点,连接,则的最小值为( ).
A. B. C. D.1
二、填空题
11.如图, 按顺时针方向转动40°得 ,点D恰好在边BC上,则∠C=________°.
12.如图,在平行四边形 中, 、 相交于点 ,点 是 的中点.若 ,则 的长是________ .
13.在平面直角坐标系 中,已知点 , ,请确定点C的坐标,使得以A , B , C , O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是________.
14.如图,在四边形中,对角线相交于点,请你添加一个条件____________,使四边形是平行四边形(填一个即可).
15.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,以这些点为顶点的平行四边形有______个.
16.已知△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D.若△ABC的一条边长为4,则点D到直线AB的距离为 __________________.
17.如图,在四边形ABCD中,AD∥BC,E、F分别是AB,DC的中点,EF分别交BD、AC于点G、H.设BC﹣AD=2m,则GH的长为______.
三、解答题
18如图,在Rt ABC中,∠ACB=90°.过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC交直线m于点E,垂足为点F,连结CD、BE.
(1)求证:CE=AD
(2)当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若点D是AB中点,当四边形BECD是正方形时,则∠A大小满足什么条件?
19.如图①,在矩形OACB中,点A、B分别在x轴、y轴正半轴上,点C在第一象限,OA=8,OB=6.
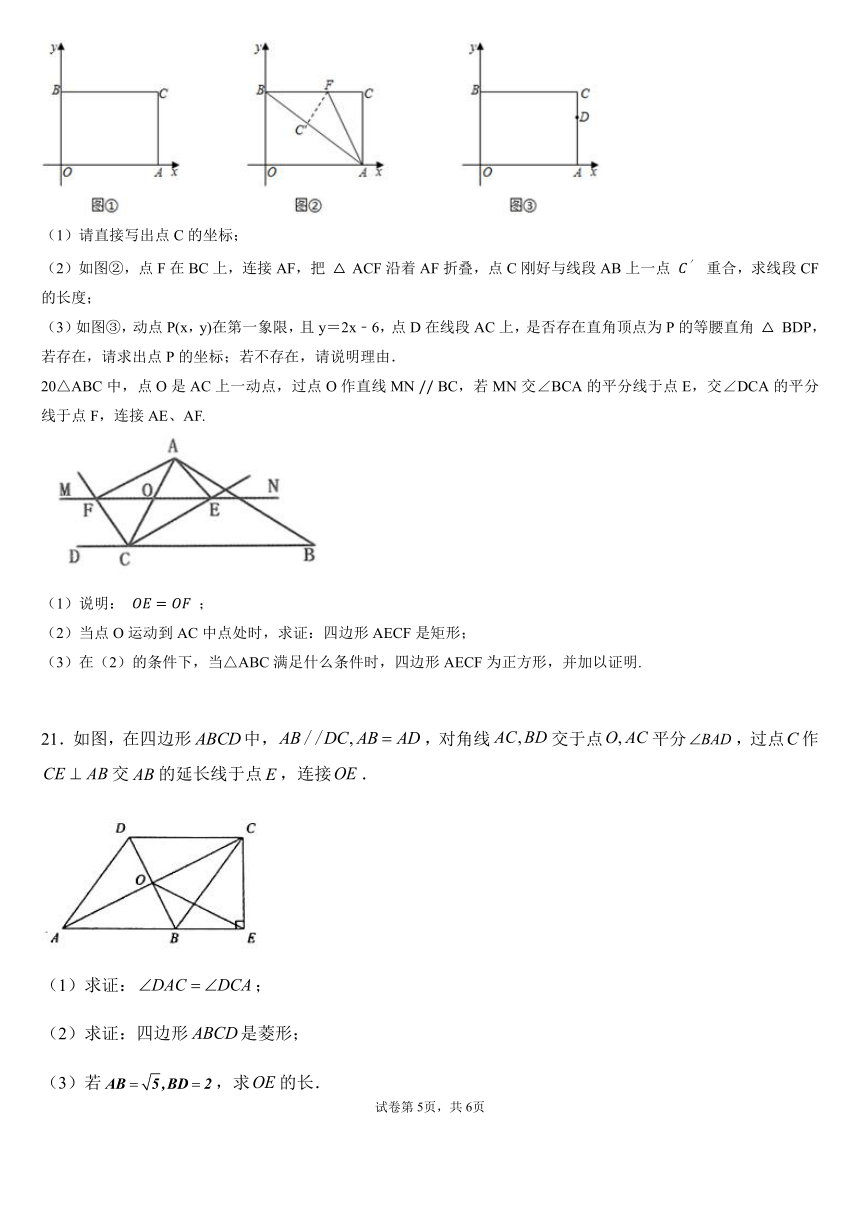
(1)请直接写出点C的坐标;
(2)如图②,点F在BC上,连接AF,把 ACF沿着AF折叠,点C刚好与线段AB上一点 重合,求线段CF的长度;
(3)如图③,动点P(x,y)在第一象限,且y=2x﹣6,点D在线段AC上,是否存在直角顶点为P的等腰直角 BDP,若存在,请求出点P的坐标;若不存在,请说明理由.
20△ABC中,点O是AC上一动点,过点O作直线MN BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.
(1)说明: ;
(2)当点O运动到AC中点处时,求证:四边形AECF是矩形;
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF为正方形,并加以证明.
21.如图,在四边形中,,对角线交于点平分,过点作交的延长线于点,连接.
(1)求证:;
(2)求证:四边形是菱形;
(3)若,求的长.
22如图,在平面直角坐标系中,直线l: 与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
(1)求出点A1的坐标,并判断点A1是否在直线l上;
(2)求出边A1C1所在直线的解析式;
(3)在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.
23如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
2.B
3.B
4.D
5.A
6.B
7.D
8.D
9.C
10.A
11.70.
12.6.
13. (4,0)或(-4,0)或(0,4).
14.(答案不唯一)
15.3
16.或2或-4或4-
17.1m
18.【答案】 (1)证明:∵m∥AB,
∴EC∥AD,
∵DE⊥BC,∴∠CFD=90°,
∵∠BCD+∠DCA=90°,∠BCD+∠CDE=90°,
∴∠DCA=∠CDE,
∴DE∥AC,
∴四边形DECA是平行四边形,
∴CE=DA;
(2)解:四边形BECD是菱形.理由如下:
∵由(1)知:四边形DECA是平行四边形,
∴CE=DA,CE∥AD,
在Rt△ABC中,∵点D是AB的中点,
∴BD=DC=DA,
又∵CE=DA,
∴CE=BD,
∴四边形BECD是平行四边形,
∵BD=CD,
∴四边形BECD是菱形.
(3)解:∠A=45°,理由如下:
∵DE∥AC,
∴∠EDB=∠A,
∵四边形BECD是正方形,
∴∠BDC=90°,∠EDB= ∠BDC=45°,
∴∠A=45°.
19【答案】 (1)C(8,6)
(2)解:∵BC=8,AC=6,
∴AB= = =10,
∵把△ACF沿着AF折叠,点C刚好与线段AB上一点C'重合,
∴AC=AC'=6,CF=C'F,∠C=∠AC'F=60°,
∴BC'=AB﹣AC'=4,
∵BF2=C'F2+C'B2 ,
∴(8﹣CF)2=CF2+16,
∴CF=3;
(3)解:设点P(a,2a﹣6),
当点P在BC下方时,如图③,过点P作EF∥BC,交y轴于E,交AC于F,
∵△BPD是等腰直角三角形,
∴BP=PD,∠BPD=90°,
∴EF∥BC,
∴∠BEP=∠BOA=90°,∠PFD=∠CAO=90°,
∴∠BPE+∠DPF=∠DPF+∠PDF,
∴∠BPE=∠PDF,
∴△BPE≌△PDF(AAS),
∴PF=BE=6﹣(2a﹣6)=12﹣2a,EP=DF,
∵EF=EP+PF=a+12﹣2a=8,
∴a=4,
∴点P(4,2);
当点P在BC的上方时,如图④,过点P作EF∥BC,交y轴于E,交AC的延长线于F,
同理可证△BPE≌△PDF,
∴BE=PF=2a﹣6﹣6=2a﹣12,
∵EF=EP+PF=a+2a﹣12=8,
∴a= ,
∴点P( , ),
综上所述:点P坐标为(4,2)或( , ).
解:(1)∵四边形OACB是矩形,
∴BC=OA=8,AC=OB=6,AC∥OB,BC∥OA,
∴点C的坐标(8,6);
20【答案】 (1)证明:∵MN∥BC,
∴∠OFC=∠FCD,∠OEC=∠ECB,
又∵CF平分∠ACD,CE平分∠ACB,
∴∠OCF=∠FCD,∠OCE=∠ECB,
∴∠OFC=∠OCF,∠OEC=∠OCE,
∴OF=OC,OE=OC,
∴OE=OF;
(2)证明:当点O运动到AC中点处时,OA=OC,由第(1)知,OE=OF,
∴四边形AECF是平行四边形,
∵OC=OF,
∴OA=OC=OF=OE,
∴AC=EF,
∴四边形AECF是矩形;
(3)证明:当点O运动到AC中点处时,且 满足∠ACB是直角的直角三角形时,四边形AECF为正方形,理由如下:
∵∠ACB=90°,
∴AC⊥BC,
∵MN∥BC,
∴AC⊥EF,
又∵由第(2)问知,当点O运动到AC中点处时,四边形AECF是矩形,
∴四边形AECF是正方形,即 满足∠ACB是直角的直角三角形时,四边形AECF为正方形.
21.(1)证明见解析(2)菱形
【解析】(1)∵四边形ABCD是正方形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠ABE=∠ADF,
在△ABE与△ADF中
,
∴△ABE≌△ADF.
(2)如图,连接AC,
四边形AECF是菱形.
理由:在正方形ABCD中,
OA=OC,OB=OD,AC⊥EF,
∴OB+BE=OD+DF,
即OE=OF,
∵OA=OC,OE=OF,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴四边形AECF是菱形.
22.(1)见解析;(2)2﹣2
【解析】证明:(1)∵把△ABC绕点A顺时针旋转得到△ADE
∴△ABC≌△ADE
∴AD=AB,AE=AC,∠DAE=∠BAC
∴∠DAE+∠BAE=∠BAC+∠BAE
∴∠DAB=∠EAC,
∵AB=AC
∴AD=AB=AC=AE
∵∠DAB=∠EAC,AD=AB,AC=AE
∴△AEC≌△ADB(SAS)
∴CE=BD
(2)∵四边形ADFC是平行四边形
∴DF=AC,AC∥BD
∴∠ABD=∠BAC=45°
∵AB=AD
∴∠DBA=∠BDA=45°
∴∠BAD=90°
∴BD=AB=2
∵DF=AC=AB=2
∴BF=BD﹣DF=2﹣2
23.(1)证明见解析 (2)2
【解析】(1)∵∠A=∠F
∴
∵,
∴
∴
∴四边形BCED是平行四边形
(2)∵BN平分∠DBC
∴
∵
∴
∴
∴.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列旋转中,旋转中心为点A的是( )
A. B.
C. D.
2.已知四边形ABCD是平行四边形,下列说法正确的有( )
①当AB=BC时,它是矩形
②AC⊥BD时,它是菱形
③当∠ABC=90°时,它是菱形
④当AC=BD时,它是正方形
A.①② B.② C.②④ D.③④
3.如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长( )
A. B.2﹣2 C.2﹣ D.2
4.以下四张扑克牌的图案,中心对称图形是( )
A. B. C. D.
5.如图,在平行四边形ABCD中,过对角线AC与BD的交点O作AC的垂线交AD于点E,连接CE,若AB=4,BC=6,则△CDE的周长是( )
A.10 B.5 C.8 D.6
6.在 ABCD中,若∠BAD与∠CDA的角平分线交于点E,则△AED的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
7.如图,,,分别是边,,上的中点,若阴影的面积为,则的面积是( )
A. B. C. D.
8.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.2 C.3 D.4
9.如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
A.9 B.18 C.36 D.48
10.如图,在中,,点分别是边上的动点,连接,点分别为的中点,连接,则的最小值为( ).
A. B. C. D.1
二、填空题
11.如图, 按顺时针方向转动40°得 ,点D恰好在边BC上,则∠C=________°.
12.如图,在平行四边形 中, 、 相交于点 ,点 是 的中点.若 ,则 的长是________ .
13.在平面直角坐标系 中,已知点 , ,请确定点C的坐标,使得以A , B , C , O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是________.
14.如图,在四边形中,对角线相交于点,请你添加一个条件____________,使四边形是平行四边形(填一个即可).
15.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,以这些点为顶点的平行四边形有______个.
16.已知△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D.若△ABC的一条边长为4,则点D到直线AB的距离为 __________________.
17.如图,在四边形ABCD中,AD∥BC,E、F分别是AB,DC的中点,EF分别交BD、AC于点G、H.设BC﹣AD=2m,则GH的长为______.
三、解答题
18如图,在Rt ABC中,∠ACB=90°.过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC交直线m于点E,垂足为点F,连结CD、BE.
(1)求证:CE=AD
(2)当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若点D是AB中点,当四边形BECD是正方形时,则∠A大小满足什么条件?
19.如图①,在矩形OACB中,点A、B分别在x轴、y轴正半轴上,点C在第一象限,OA=8,OB=6.
(1)请直接写出点C的坐标;
(2)如图②,点F在BC上,连接AF,把 ACF沿着AF折叠,点C刚好与线段AB上一点 重合,求线段CF的长度;
(3)如图③,动点P(x,y)在第一象限,且y=2x﹣6,点D在线段AC上,是否存在直角顶点为P的等腰直角 BDP,若存在,请求出点P的坐标;若不存在,请说明理由.
20△ABC中,点O是AC上一动点,过点O作直线MN BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.
(1)说明: ;
(2)当点O运动到AC中点处时,求证:四边形AECF是矩形;
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF为正方形,并加以证明.
21.如图,在四边形中,,对角线交于点平分,过点作交的延长线于点,连接.
(1)求证:;
(2)求证:四边形是菱形;
(3)若,求的长.
22如图,在平面直角坐标系中,直线l: 与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
(1)求出点A1的坐标,并判断点A1是否在直线l上;
(2)求出边A1C1所在直线的解析式;
(3)在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.
23如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
2.B
3.B
4.D
5.A
6.B
7.D
8.D
9.C
10.A
11.70.
12.6.
13. (4,0)或(-4,0)或(0,4).
14.(答案不唯一)
15.3
16.或2或-4或4-
17.1m
18.【答案】 (1)证明:∵m∥AB,
∴EC∥AD,
∵DE⊥BC,∴∠CFD=90°,
∵∠BCD+∠DCA=90°,∠BCD+∠CDE=90°,
∴∠DCA=∠CDE,
∴DE∥AC,
∴四边形DECA是平行四边形,
∴CE=DA;
(2)解:四边形BECD是菱形.理由如下:
∵由(1)知:四边形DECA是平行四边形,
∴CE=DA,CE∥AD,
在Rt△ABC中,∵点D是AB的中点,
∴BD=DC=DA,
又∵CE=DA,
∴CE=BD,
∴四边形BECD是平行四边形,
∵BD=CD,
∴四边形BECD是菱形.
(3)解:∠A=45°,理由如下:
∵DE∥AC,
∴∠EDB=∠A,
∵四边形BECD是正方形,
∴∠BDC=90°,∠EDB= ∠BDC=45°,
∴∠A=45°.
19【答案】 (1)C(8,6)
(2)解:∵BC=8,AC=6,
∴AB= = =10,
∵把△ACF沿着AF折叠,点C刚好与线段AB上一点C'重合,
∴AC=AC'=6,CF=C'F,∠C=∠AC'F=60°,
∴BC'=AB﹣AC'=4,
∵BF2=C'F2+C'B2 ,
∴(8﹣CF)2=CF2+16,
∴CF=3;
(3)解:设点P(a,2a﹣6),
当点P在BC下方时,如图③,过点P作EF∥BC,交y轴于E,交AC于F,
∵△BPD是等腰直角三角形,
∴BP=PD,∠BPD=90°,
∴EF∥BC,
∴∠BEP=∠BOA=90°,∠PFD=∠CAO=90°,
∴∠BPE+∠DPF=∠DPF+∠PDF,
∴∠BPE=∠PDF,
∴△BPE≌△PDF(AAS),
∴PF=BE=6﹣(2a﹣6)=12﹣2a,EP=DF,
∵EF=EP+PF=a+12﹣2a=8,
∴a=4,
∴点P(4,2);
当点P在BC的上方时,如图④,过点P作EF∥BC,交y轴于E,交AC的延长线于F,
同理可证△BPE≌△PDF,
∴BE=PF=2a﹣6﹣6=2a﹣12,
∵EF=EP+PF=a+2a﹣12=8,
∴a= ,
∴点P( , ),
综上所述:点P坐标为(4,2)或( , ).
解:(1)∵四边形OACB是矩形,
∴BC=OA=8,AC=OB=6,AC∥OB,BC∥OA,
∴点C的坐标(8,6);
20【答案】 (1)证明:∵MN∥BC,
∴∠OFC=∠FCD,∠OEC=∠ECB,
又∵CF平分∠ACD,CE平分∠ACB,
∴∠OCF=∠FCD,∠OCE=∠ECB,
∴∠OFC=∠OCF,∠OEC=∠OCE,
∴OF=OC,OE=OC,
∴OE=OF;
(2)证明:当点O运动到AC中点处时,OA=OC,由第(1)知,OE=OF,
∴四边形AECF是平行四边形,
∵OC=OF,
∴OA=OC=OF=OE,
∴AC=EF,
∴四边形AECF是矩形;
(3)证明:当点O运动到AC中点处时,且 满足∠ACB是直角的直角三角形时,四边形AECF为正方形,理由如下:
∵∠ACB=90°,
∴AC⊥BC,
∵MN∥BC,
∴AC⊥EF,
又∵由第(2)问知,当点O运动到AC中点处时,四边形AECF是矩形,
∴四边形AECF是正方形,即 满足∠ACB是直角的直角三角形时,四边形AECF为正方形.
21.(1)证明见解析(2)菱形
【解析】(1)∵四边形ABCD是正方形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠ABE=∠ADF,
在△ABE与△ADF中
,
∴△ABE≌△ADF.
(2)如图,连接AC,
四边形AECF是菱形.
理由:在正方形ABCD中,
OA=OC,OB=OD,AC⊥EF,
∴OB+BE=OD+DF,
即OE=OF,
∵OA=OC,OE=OF,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴四边形AECF是菱形.
22.(1)见解析;(2)2﹣2
【解析】证明:(1)∵把△ABC绕点A顺时针旋转得到△ADE
∴△ABC≌△ADE
∴AD=AB,AE=AC,∠DAE=∠BAC
∴∠DAE+∠BAE=∠BAC+∠BAE
∴∠DAB=∠EAC,
∵AB=AC
∴AD=AB=AC=AE
∵∠DAB=∠EAC,AD=AB,AC=AE
∴△AEC≌△ADB(SAS)
∴CE=BD
(2)∵四边形ADFC是平行四边形
∴DF=AC,AC∥BD
∴∠ABD=∠BAC=45°
∵AB=AD
∴∠DBA=∠BDA=45°
∴∠BAD=90°
∴BD=AB=2
∵DF=AC=AB=2
∴BF=BD﹣DF=2﹣2
23.(1)证明见解析 (2)2
【解析】(1)∵∠A=∠F
∴
∵,
∴
∴
∴四边形BCED是平行四边形
(2)∵BN平分∠DBC
∴
∵
∴
∴
∴.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
