第九章 不等式与不等式组 复习小结 课件(共25张PPT)
文档属性
| 名称 | 第九章 不等式与不等式组 复习小结 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
第九章 不等式与不等式组
复习小结
人教版 七年级下册
【问题1】本章学习了哪些知识?
它们之间的联系是什么?
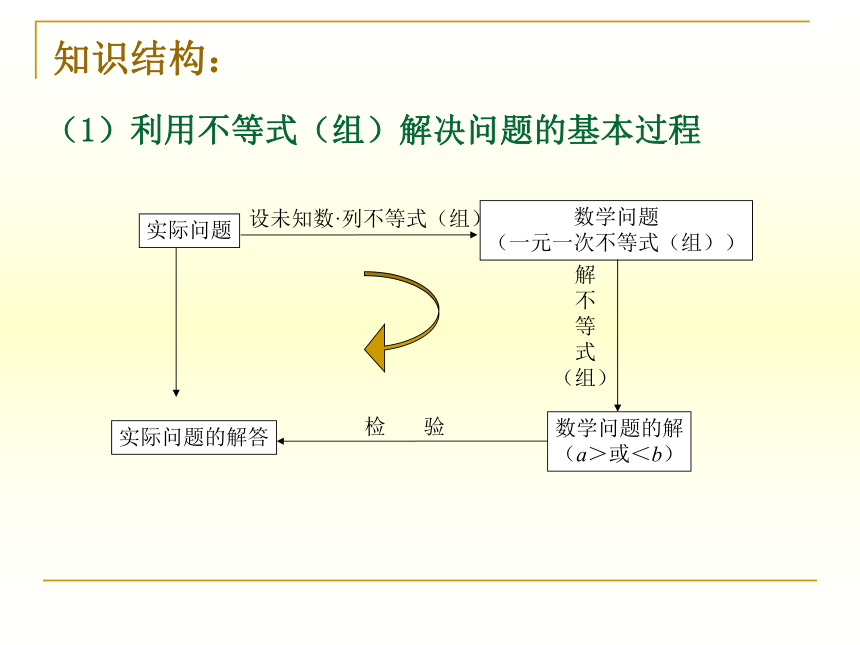
(1)利用不等式(组)解决问题的基本过程
知识结构:
实际问题
解
不
等
式
(组)
数学问题
(一元一次不等式(组))
检 验
设未知数·列不等式(组)
实际问题的解答
数学问题的解
(a>或<b)
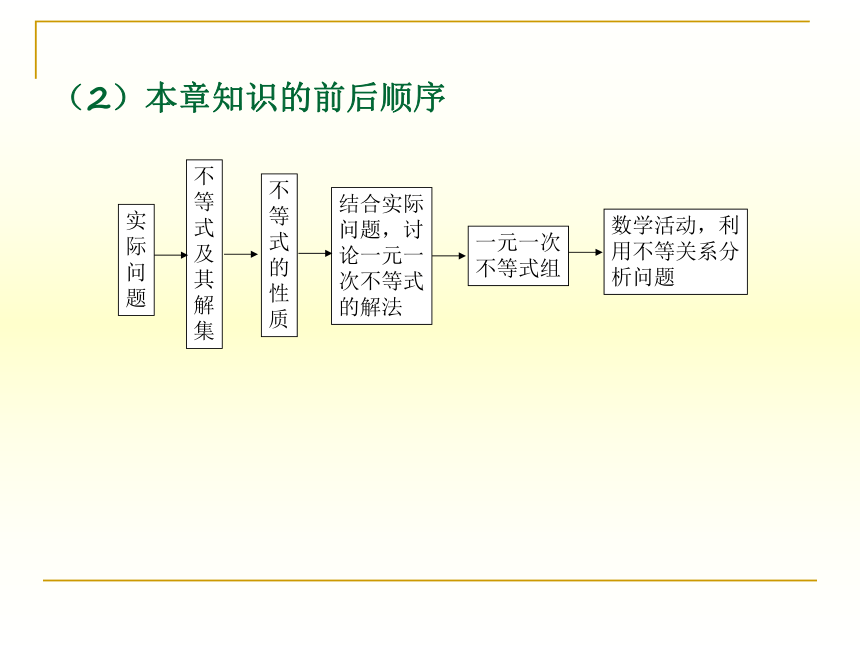
(2)本章知识的前后顺序
实
际
问
题
不
等
式
及
其
解
集
不
等
式
的
性
质
结合实际
问题,讨
论一元一
次不等式
的解法
一元一次
不等式组
数学活动,利
用不等关系分
析问题
知识要点:
1. 你知道本章学习了哪些概念吗?
其中,不等式的解与不等式的解集的区别在哪里?
2. 不等式有哪些性质?
不等式的性质与等式的性质相比较,
你知道它们的异同点是什么吗?
3.不等式(组)的解法及解集的几何表示.
⑴ 你会解一元一次不等式吗?
与 解一元一次方程的基本思想(化归思想)是否一致?
一元一次不等式的解法中,特别需要注意
的是哪一步?
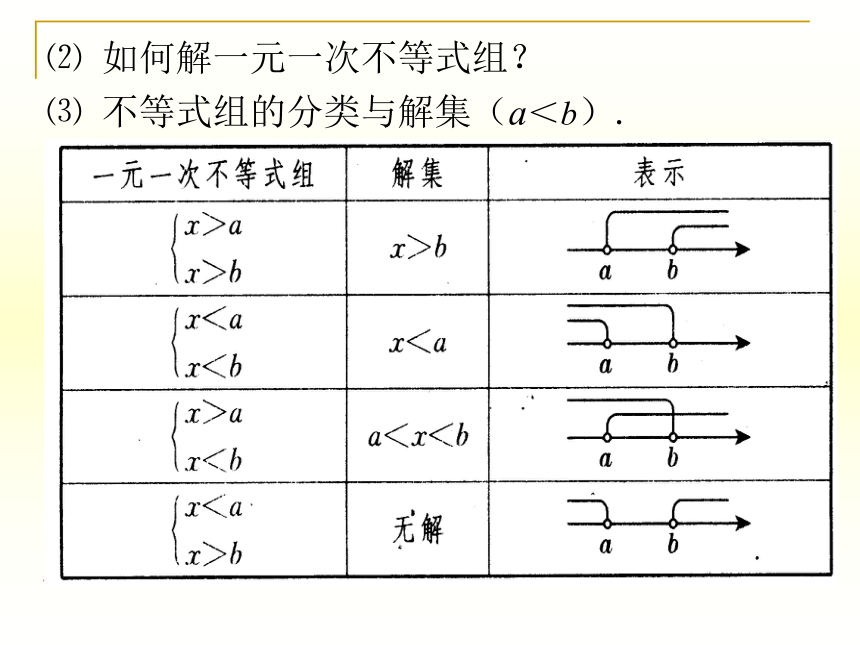
⑵ 如何解一元一次不等式组?
⑶ 不等式组的分类与解集(a<b).
【问题2】请你仔细思考,填好下面
的每一个空.
答案:
【问题3】你会解一元一次不等式
(组)吗?
解不等式 ,并将其
解集表示在数轴上.
答案:x≤-2.
解不等式组
.
答案:
【问题4】你知道如何求正数解、负
数解和整数解吗?
求不等式 的非正的整数解.
解不等式,得x>-4,
所以非正的整数解是:-3,-2,-1,0 .
求使方程组 的
解 、 都是正数的 的取值范围.
【问题5】用不等式(组)的知识解
决实际问题的基本过程是
什么?
某工程队计划在10天内修路6 km,施工前2天修完1.2 km,计划发生变化,准备提前2天完成修路任务,以后几天内平均每天至少要修路多少千米?
分析:设以后几天内平均每天至少修路 km.
(10-2-2)
天内
6-1.2
改变计划后
10天内
6
原计划
工作效率
(平均每天至少)
时间
(天)
路程
(km)
x
6
10
x
答案:每天至少修0.8 km.
若干学生分住宿舍,每间4人余20人,每
间8人有一间不空也不满,则宿舍有多少间,
学生有多少人?
分析:
答案:宿舍有6间,人数44人.
【问题6】通过对本章内容的复习,
你有哪些新的收获?
复习题9第1题的(1)(3),第3题的(2)(4),第4、7、8题.
谢 谢!
祝大家学习愉快
第九章 不等式与不等式组
复习小结
人教版 七年级下册
【问题1】本章学习了哪些知识?
它们之间的联系是什么?
(1)利用不等式(组)解决问题的基本过程
知识结构:
实际问题
解
不
等
式
(组)
数学问题
(一元一次不等式(组))
检 验
设未知数·列不等式(组)
实际问题的解答
数学问题的解
(a>或<b)
(2)本章知识的前后顺序
实
际
问
题
不
等
式
及
其
解
集
不
等
式
的
性
质
结合实际
问题,讨
论一元一
次不等式
的解法
一元一次
不等式组
数学活动,利
用不等关系分
析问题
知识要点:
1. 你知道本章学习了哪些概念吗?
其中,不等式的解与不等式的解集的区别在哪里?
2. 不等式有哪些性质?
不等式的性质与等式的性质相比较,
你知道它们的异同点是什么吗?
3.不等式(组)的解法及解集的几何表示.
⑴ 你会解一元一次不等式吗?
与 解一元一次方程的基本思想(化归思想)是否一致?
一元一次不等式的解法中,特别需要注意
的是哪一步?
⑵ 如何解一元一次不等式组?
⑶ 不等式组的分类与解集(a<b).
【问题2】请你仔细思考,填好下面
的每一个空.
答案:
【问题3】你会解一元一次不等式
(组)吗?
解不等式 ,并将其
解集表示在数轴上.
答案:x≤-2.
解不等式组
.
答案:
【问题4】你知道如何求正数解、负
数解和整数解吗?
求不等式 的非正的整数解.
解不等式,得x>-4,
所以非正的整数解是:-3,-2,-1,0 .
求使方程组 的
解 、 都是正数的 的取值范围.
【问题5】用不等式(组)的知识解
决实际问题的基本过程是
什么?
某工程队计划在10天内修路6 km,施工前2天修完1.2 km,计划发生变化,准备提前2天完成修路任务,以后几天内平均每天至少要修路多少千米?
分析:设以后几天内平均每天至少修路 km.
(10-2-2)
天内
6-1.2
改变计划后
10天内
6
原计划
工作效率
(平均每天至少)
时间
(天)
路程
(km)
x
6
10
x
答案:每天至少修0.8 km.
若干学生分住宿舍,每间4人余20人,每
间8人有一间不空也不满,则宿舍有多少间,
学生有多少人?
分析:
答案:宿舍有6间,人数44人.
【问题6】通过对本章内容的复习,
你有哪些新的收获?
复习题9第1题的(1)(3),第3题的(2)(4),第4、7、8题.
谢 谢!
祝大家学习愉快
