(安徽专版)2021-2022学年沪科版七年级数学下册期中测试卷(word版 含解析)
文档属性
| 名称 | (安徽专版)2021-2022学年沪科版七年级数学下册期中测试卷(word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 208.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 23:54:40 | ||
图片预览



文档简介
2021-2022学年沪科版七年级数学下册期中测试卷(安徽专版)
考试时间:120分钟
一、选择题(每小题4分,共40分)
1.下列数中,是无理数的是( )
A. B.
C.﹣2.171171117 D.
2.下列运算正确的是( )
A.=±2 B.(﹣3)3=27 C.=3 D.=2
3.若a<b,c≠0,则下列不等式不一定成立的是( )
A.a+c<b+c B.a﹣c<b﹣c C.ac2<bc2 D.<
4.估计﹣1的值在( )
A.2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
5.下列运算正确的是( )
A.2a﹣a=2 B.(a﹣1)2=a2﹣1
C.(2a3)2=4a6 D.a6÷a3=a2
6.已知2a=5,2b=10,2c=50,那么a、b、c之间满足的等量关系是( )
A.ab=c B.a+b=c
C.a:b:c=1:2:10 D.a2b2=c2
7.不等式2(1﹣2x)≤12﹣6x最大整数解是的解,则a的值是( )
A. B. C.0 D.﹣2
8.某学校准备购进单价分别为5元和7元的A、B两种笔记本共50本作为奖品发放给学生,要求A种笔记本的数量不多于B种笔记本数量的3倍,不少于B种笔记本数量的2倍,则不同的购买方案种数为( )
A.1 B.2 C.3 D.4
9.已知a1为实数,规定运算:,,,,…,an=1﹣.按上述方法计算:当a1=3时,a2022的值等于( )
A. B. C. D.
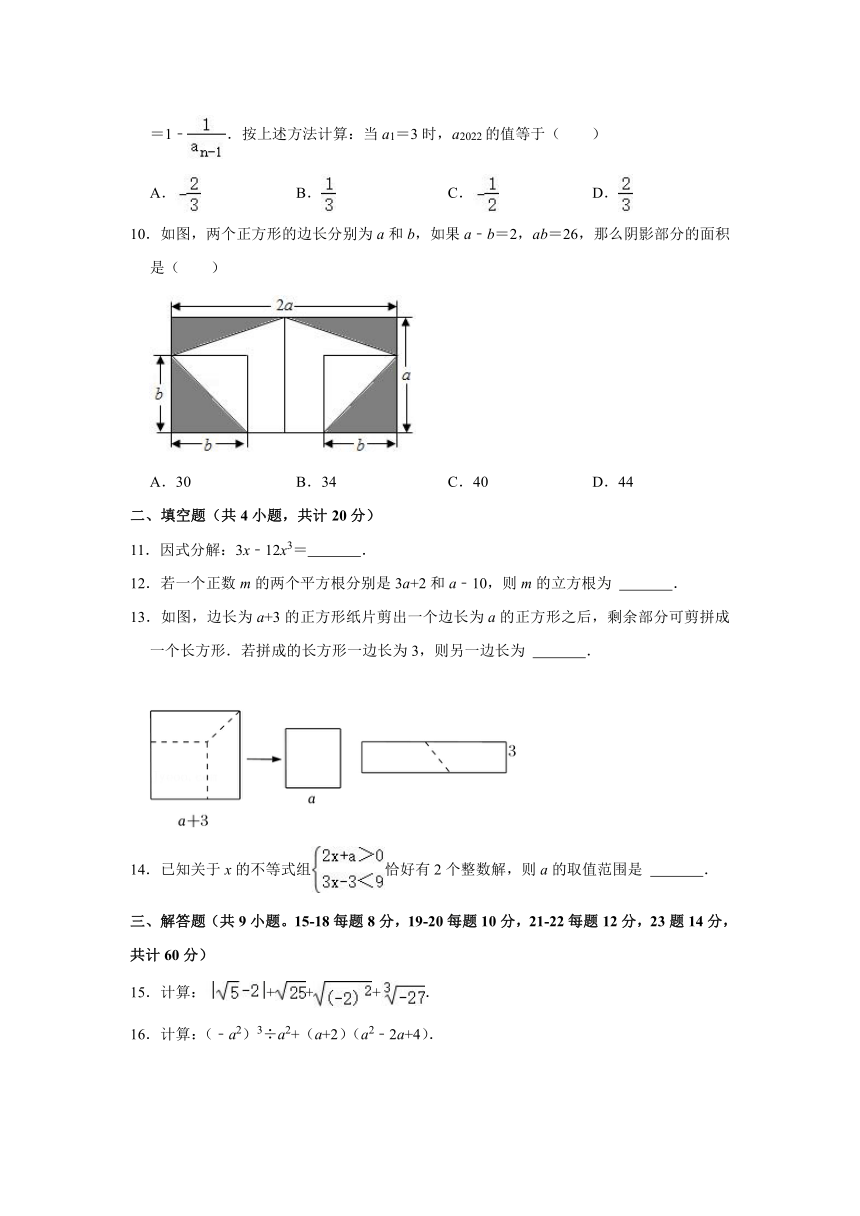
10.如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
二、填空题(共4小题,共计20分)
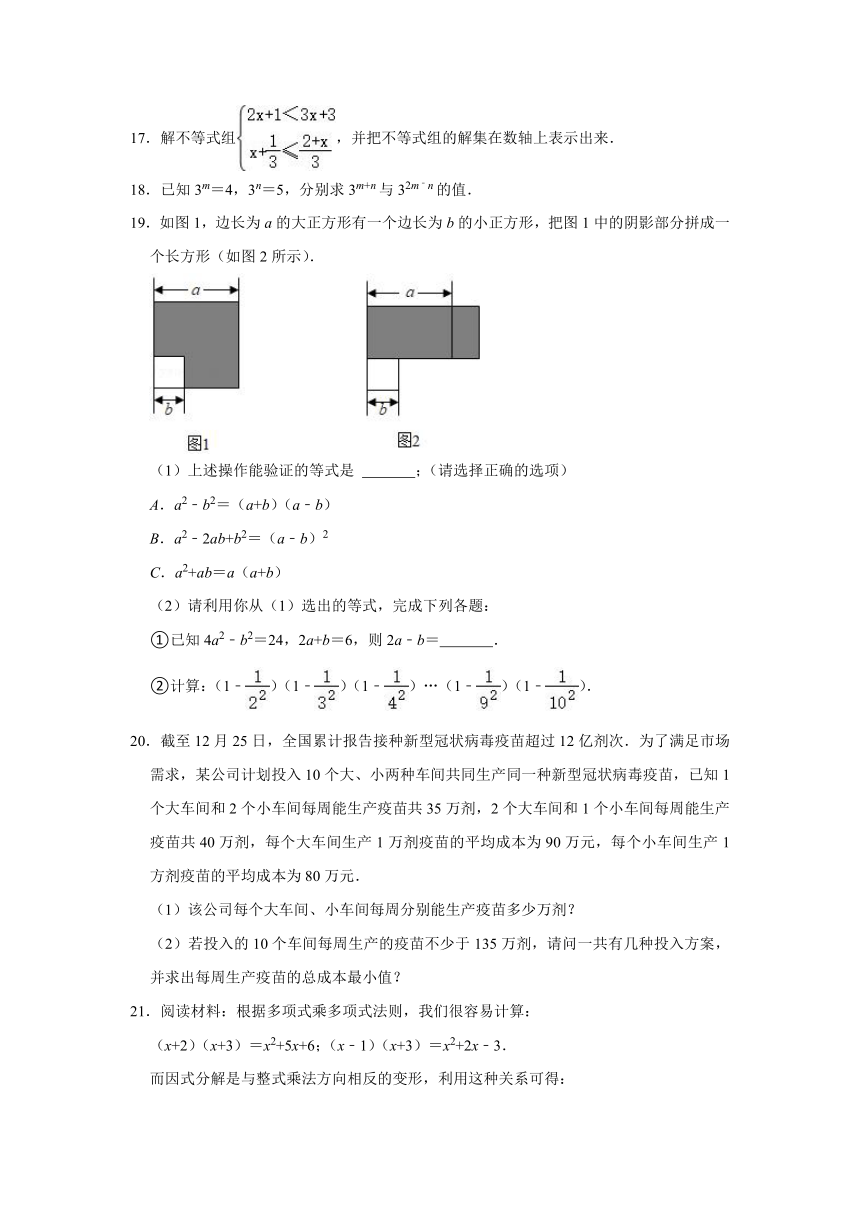
11.因式分解:3x﹣12x3= .
12.若一个正数m的两个平方根分别是3a+2和a﹣10,则m的立方根为 .
13.如图,边长为a+3的正方形纸片剪出一个边长为a的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为3,则另一边长为 .
14.已知关于x的不等式组恰好有2个整数解,则a的取值范围是 .
解答题(共9小题。15-18每题8分,19-20每题10分,21-22每题12分,23题14分,共计60分)
15.计算:+++.
16.计算:(﹣a2)3÷a2+(a+2)(a2﹣2a+4).
17.解不等式组,并把不等式组的解集在数轴上表示出来.
18.已知3m=4,3n=5,分别求3m+n与32m﹣n的值.
19.如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 ;(请选择正确的选项)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= .
②计算:(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).
20.截至12月25日,全国累计报告接种新型冠状病毒疫苗超过12亿剂次.为了满足市场需求,某公司计划投入10个大、小两种车间共同生产同一种新型冠状病毒疫苗,已知1个大车间和2个小车间每周能生产疫苗共35万剂,2个大车间和1个小车间每周能生产疫苗共40万剂,每个大车间生产1万剂疫苗的平均成本为90万元,每个小车间生产1方剂疫苗的平均成本为80万元.
(1)该公司每个大车间、小车间每周分别能生产疫苗多少万剂?
(2)若投入的10个车间每周生产的疫苗不少于135万剂,请问一共有几种投入方案,并求出每周生产疫苗的总成本最小值?
21.阅读材料:根据多项式乘多项式法则,我们很容易计算:
(x+2)(x+3)=x2+5x+6;(x﹣1)(x+3)=x2+2x﹣3.
而因式分解是与整式乘法方向相反的变形,利用这种关系可得:
x2+5x+6=(x+2)(x+3);x2+2x﹣3=(x﹣1)(x+3).
通过这样的关系我们可以将某些二次项系数是1的二次三项式分解因式.如将式子x2+2x﹣3分解因式.这个式子的二次项系数是1=1×1,常数项﹣3=(﹣1)×3,一次项系数2=(﹣1)+3,可以用下图十字相乘的形式表示为:
先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求和,使其等于一次项系数,然后横向书写.这样,我们就可以得到:x2+2x﹣3=(x﹣1)(x+3).
利用这种方法,将下列多项式分解因式:
(1)x2+7x+10= ;
(2)x2﹣2x﹣3= ;
(3)y2﹣7y+12= ;
(4)x2+7x﹣18= .
22.如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示,设点B所表示的数为m.
(1)实数m的值是 .
(2)求|m+1|+|m﹣1|的值;
(3)在数轴上还有C、D两点分别表示实数c和d,且有|2c+4|与互为相反数,求2c+3d的平方根.
23.如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①x﹣(3x+1)=﹣5;②+1=0;③3x﹣1=0中,不等式组的关联方程是 (填序号).
(2)若不等式组的某个关联方程的根是整数,则这个关联方程可以是 (写出一个即可)
(3)若方程﹣x=x,3+x=2(x+)都是关于x的不等式组的关联方程,直接写出m的取值范围.
2021-2022学年沪科版七年级数学下册期中测试卷(安徽专版)
考试时间:120分钟
选择题(每小题4分,共40分)
1.下列数中,是无理数的是( )
A. B.
C.﹣2.171171117 D.
【分析】理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】解:A.是分数,属于有理数,故本选项不合题意;
B.,是整数,属于有理数,故本选项不合题意;
C.﹣2.171171117是有限小数,属于有理数,故本选项不合题意;
D.是无理数,故本选项符合题意.
故选:D.
【点评】本题主要考查了无理数.解题的关键是掌握无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
2.下列运算正确的是( )
A.=±2 B.(﹣3)3=27 C.=3 D.=2
【分析】根据算术平方根、立方根、有理数的乘方的定义解决此题.
【解答】解:A.根据算术平方根的定义,,那么A错误,故A不符合题意.
B.根据有理数的乘方,(﹣3)3=﹣27,那么B错误,故B不符合题意.
C.根据立方根的定义,,那么C错误,故C不符合题意.
D.根据算术平方根的定义,,那么D正确,故D符合题意.
故选:D.
【点评】本题主要考查算术平方根、立方根、有理数的乘方,熟练掌握算术平方根、立方根、有理数的乘方的定义是解决本题的关键.
3.若a<b,c≠0,则下列不等式不一定成立的是( )
A.a+c<b+c B.a﹣c<b﹣c C.ac2<bc2 D.<
【分析】根据不等式的基本性质判断即可.
【解答】解:A选项,∵a<b,
∴a+c<b+c,故该选项不符合题意;
B选项,∵a<b,
∴a﹣c<b﹣c,故该选项不符合题意;
C选项,∵a<b,c≠0,
∴ac2<bc2,故该选项不符合题意;
D选项,∵a<b,c≠0,
∴当c>0时,<;
当c<0时,>,故该选项符合题意;
故选:D.
【点评】本题考查了不等式的基本性质,掌握①不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变;②不等式的两边同时乘(或除以)同一个正数,不等号的方向不变;③不等式的两边同时乘(或除以)同一个负数,不等号的方向改变是解题的关键.
4.估计﹣1的值在( )
A.2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
【分析】估算出的值进行计算即可解答.
【解答】解:∵25<26<36,
∴5<<6,
∴4<﹣1<5,
∴估计﹣1的值在:4到5之间,
故选:C.
【点评】本题考查了估算无理数的大小,熟练掌握平方数是解题的关键.
5.下列运算正确的是( )
A.2a﹣a=2 B.(a﹣1)2=a2﹣1
C.(2a3)2=4a6 D.a6÷a3=a2
【分析】根据合并同类项法则、完全平方公式、积的乘方与幂的乘方法法则、同底数幂的除法法则解决此题.
【解答】解:A.根据合并同类项法则,2a﹣a=a,那么A错误,故A不符合题意.
B.根据完全平方公式,(a﹣1)2=a2+1﹣2a,那么B错误,故B不符合题意.
C.根据积的乘方与幂的乘方,(2a3)2=4a6,那么C正确,故C符合题意.
D.根据同底数幂的除法,a6÷a3=a3,那么D错误,故D不符合题意.
故选:C.
【点评】本题主要考查合并同类项、完全平方公式、积的乘方与幂的乘方、同底数幂的除法,熟练掌握合并同类项法则、完全平方公式、积的乘方与幂的乘方、同底数幂的除法法则是解决本题的关键.
6.已知2a=5,2b=10,2c=50,那么a、b、c之间满足的等量关系是( )
A.ab=c B.a+b=c
C.a:b:c=1:2:10 D.a2b2=c2
【分析】根据5×10=50,得到2a 2b=2c,根据同底数幂的乘法法则得到2a+b=2c,从而a+b=c.
【解答】解:∵5×10=50,
∴2a 2b=2c,
∴2a+b=2c,
∴a+b=c,
故选:B.
【点评】本题考查了同底数幂的乘法,掌握am an=am+n是解题的关键.
7.不等式2(1﹣2x)≤12﹣6x最大整数解是的解,则a的值是( )
A. B. C.0 D.﹣2
【分析】根据不等式2(1﹣2x)≤12﹣6x求得x的最大整数解,代入是,即可求得a的值.
【解答】解:2(1﹣2x)≤12﹣6x,
2﹣4x≤12﹣6x,
6x﹣4x≤12﹣2,
2x≤10,
x≤5,
∴不等式2(1﹣2x)≤12﹣6x最大整数解是5,
把x=5代入得,﹣5=,
∴=5,
∴a=,
故选:B.
【点评】本题考查了一元一次不等式的整数解,一元一次方程的解,通过解不等式求得不等式的最大整数解是解题的关键.
8.某学校准备购进单价分别为5元和7元的A、B两种笔记本共50本作为奖品发放给学生,要求A种笔记本的数量不多于B种笔记本数量的3倍,不少于B种笔记本数量的2倍,则不同的购买方案种数为( )
A.1 B.2 C.3 D.4
【分析】设购进A种笔记本为x本,则购进B种笔记本为(50﹣x)本,由题意:A种笔记本的数量不多于B种笔记本数量的3倍,不少于B种笔记本数量的2倍,列出不等式组,解不等式组,取正整数解即可.
【解答】解:设购进A种笔记本为x本,则购进B种笔记本为(50﹣x)本,
由题意得:,
解得:33≤x≤37,
∵x为正整数,
∴x的取值为34,、35、36、37,
则不同的购买方案种数为4种,
故选:D.
【点评】本题考查了一元一次不等式组的应用,找出数量关系,列出一元一次不等式组是解题的关键.
9.已知a1为实数,规定运算:,,,,…,an=1﹣.按上述方法计算:当a1=3时,a2022的值等于( )
A. B. C. D.
【分析】把a1=3代入进行计算,找出规律即可解答.
【解答】解:a1=3,
a2=1﹣=1﹣=,
a3=1﹣=1﹣=,
a4=1﹣=1﹣=3,
...
∴2022÷3=674,
∴a2022=,
故选:C.
【点评】本题考查了实数的运算,规律型:数字变化类,把a1=3代入进行计算从数字找规律是解题的关键.
10.如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
【分析】由图可得阴影部分面积为4个直角三角形面积的和.
【解答】解:如图,
∵a﹣b=2,ab=26,
∴a2﹣2ab+b2=4,
∴a2+b2=4+2ab=4+52=56,
阴影部分的面积=S△ABC+S△CDM+S△AEF+S△GHM
=2×(a﹣b)×a+2×b×b
=a(a﹣b)+b2
=a2+b2﹣ab
=56﹣26
=30.
故选:A.
【点评】本题主要考查了完全平方公式的几何背景的应用,根据题意列出阴影部分面积的表达式是解决本题的关键.
二.填空题(共4小题)
11.因式分解:3x﹣12x3= 3x(1+2x)(1﹣2x) .
【分析】先提公因式,然后利用平方差公式继续分解即可.
【解答】解:3x﹣12x3
=3x(1﹣4x2)
=3x(1+2x)(1﹣2x),
故答案为:3x(1+2x)(1﹣2x).
【点评】本题考查了提公因式法与公式法的综合运用,一定要注意如果多项式的各项含有公因式,必须先提公因式.
12.若一个正数m的两个平方根分别是3a+2和a﹣10,则m的立方根为 4 .
【分析】根据平方根的性质以及立方根的定义解决此题.
【解答】解:由题意得,3a+2+a﹣10=0.
∴a=2.
∴3a+2=8.
∴m=64.
∴m的立方根为4.
故答案为:4.
【点评】本题主要考查平方根、立方根,熟练掌握平方根的性质、立方根的定义是解决本题的关键.
13.如图,边长为a+3的正方形纸片剪出一个边长为a的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为3,则另一边长为 2a+3 .
【分析】根据拼图中各个部分之间的关系得出答案.
【解答】解:如图,将剩余部分拼成一个长方形.这个长方形一边长为3,另一边长为a+(a+3),
即2a+3,
故答案为:2a+3.
【点评】本题考查平方差公式的几何背景,理解拼图中各个部分之间的关系是解决问题的关键.
14.已知关于x的不等式组恰好有2个整数解,则a的取值范围是 ﹣4<a≤﹣2 .
【分析】先求出不等式组的解集,根据不等式组有2个整数解得出1≤﹣<2,再求出a的范围即可.
【解答】解:,
解不等式①,得x>﹣,
解不等式②,得x<4,
所以不等式组的解集是﹣<x<4,
∵关于x的不等式组恰好有2个整数解(整数解是2,3),
∴1≤﹣<2,
解得:﹣4<a≤﹣2,
故答案为:﹣4<a≤﹣2.
【点评】本题考查了解一元一次不等式组和不等式组的整数解,能得出关于a的不等式组是解此题的关键.
三.解答题(共9小题)
15.计算:+++.
【分析】先计算绝对值和开方,再计算加减即可.
【解答】解:+++
=﹣2+5+2﹣3
=+2.
【点评】此题考查了绝对值、开方及加减混合运算能力,关键是能确定正确的运算顺序和能对以上知识熟练准确计算.
16.计算:(﹣a2)3÷a2+(a+2)(a2﹣2a+4).
【分析】根据多项式乘多项式、幂的乘方与积的乘方以及同底数幂的除法法则分别进行计算,即可得出答案.
【解答】解:(﹣a2)3÷a2+(a+2)(a2﹣2a+4)
=﹣a6÷a2+a3﹣2a2+4a+2a2﹣4a+8
=﹣a4+a3﹣2a2+4a+2a2﹣4a+8
=﹣a4+a3+8.
【点评】此题考查了多项式乘多项式、幂的乘方与积的乘方以及同底数幂的除法,熟练掌握运算法则是解题的关键.
17.解不等式组,并把不等式组的解集在数轴上表示出来.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【解答】解:解不等式2x+1<3x+3,得:x>﹣2,
解不等式x+≤,得:x≤0.5,
则不等式组的解集为﹣2<x≤0.5,
将不等式组的解集表示在数轴上如下:
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
18.已知3m=4,3n=5,分别求3m+n与32m﹣n的值.
【分析】利用同底数幂的乘法的法则,同底数幂的除法的法则,幂的乘方的法则对所求的式子进行整理,再代入运算即可.
【解答】解:当3m=4,3n=5时,
3m+n
=3m×3n
=4×5
=20;
32m﹣n
=32m÷3n
=(3m)2÷3n
=42÷5
=16÷5
=.
【点评】本题主要考查同底数幂的除法,同底数幂的乘法,幂的乘方,解答的关键是对相应的运算法则的掌握.
19.如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 A ;(请选择正确的选项)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= 4 .
②计算:(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).
【分析】(1)用两种方法表示阴影部分的面积即可.
(2)利用(1)中得到的平方差公式计算.
【解答】解:(1)图1中阴影部分的面积=a2﹣b2,图②中阴影部分的面积=(a+b)(a﹣b).
∴a2﹣b2=(a+b)(a﹣b).
故选A.
(2)①∵(2a+b)(2a﹣b)=4a2﹣b2.
∴6(2a﹣b)=24,
∴2a﹣b=24÷6=4.
故答案为:4.
②=
=
=
=.
【点评】本题考查平方差公式及其应用,用两种方法表示同一个图形面积,再用所得公式完成计算是求解本题的关键.
20.截至12月25日,全国累计报告接种新型冠状病毒疫苗超过12亿剂次.为了满足市场需求,某公司计划投入10个大、小两种车间共同生产同一种新型冠状病毒疫苗,已知1个大车间和2个小车间每周能生产疫苗共35万剂,2个大车间和1个小车间每周能生产疫苗共40万剂,每个大车间生产1万剂疫苗的平均成本为90万元,每个小车间生产1方剂疫苗的平均成本为80万元.
(1)该公司每个大车间、小车间每周分别能生产疫苗多少万剂?
(2)若投入的10个车间每周生产的疫苗不少于135万剂,请问一共有几种投入方案,并求出每周生产疫苗的总成本最小值?
【分析】(1)设该公司每个大车间每周能生产疫苗x万剂,每个小车间每周能生产疫苗y万剂,根据“1个大车间和2个小车间每周能生产疫苗共35万剂,2个大车间和1个小车间每周能生产疫苗共40方剂”,即可得出关于x,y的二元一次方程组,解之即可求出该公司每个大车间、小车间每周生产疫苗的数量;
(2)设投入m个大车间,则投入小车间(10﹣m)个,根据每周生产的疫苗不少于135万剂,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,结合m,(10﹣m)均为正整数,即可得出投入方案的个数,再求出各投入方案每周生产疫苗的总成本,比较后即可得出每周生产疫苗的总成本最小值为11850万元.
【解答】解:(1)设该公司每个大车间每周能生产疫苗x万剂,每个小车间每周能生产疫苗y万剂,
依题意得:,
解得:.
答:该公司每个大车间每周能生产疫苗15万剂,每个小车间每周能生产疫苗10万剂.
(2)设投入m个大车间,则投入小车间(10﹣m)个,
依题意得:15m+10(10﹣m)≥135,
解得:m≥7.
又∵m,(10﹣m)均为正整数,
∴m可以为7,8,9,
∴共有3种投入方案,
方案1:投入7个大车间,3个小车间,每周生产疫苗的总成本90×15×7+80×10×3=11850(万元);
方案2:投入8个大车间,2个小车间,每周生产疫苗的总成本90×15×8+80×10×2=12400(万元);
方案3:投入9个大车间,1个小车间,每周生产疫苗的总成本90×15×9+80×10×1=12950(万元).
∵11850<12400<12950,
∴一共有3种投入方案,每周生产疫苗的总成本最小值为11850万元.
【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
21.阅读材料:根据多项式乘多项式法则,我们很容易计算:
(x+2)(x+3)=x2+5x+6;(x﹣1)(x+3)=x2+2x﹣3.
而因式分解是与整式乘法方向相反的变形,利用这种关系可得:
x2+5x+6=(x+2)(x+3);x2+2x﹣3=(x﹣1)(x+3).
通过这样的关系我们可以将某些二次项系数是1的二次三项式分解因式.如将式子x2+2x﹣3分解因式.这个式子的二次项系数是1=1×1,常数项﹣3=(﹣1)×3,一次项系数2=(﹣1)+3,可以用下图十字相乘的形式表示为:
先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求和,使其等于一次项系数,然后横向书写.这样,我们就可以得到:x2+2x﹣3=(x﹣1)(x+3).
利用这种方法,将下列多项式分解因式:
(1)x2+7x+10= (x+2)(x+5) ;
(2)x2﹣2x﹣3= (x﹣3)(x+1) ;
(3)y2﹣7y+12= (y﹣3)(y﹣4) ;
(4)x2+7x﹣18= (x+9)(x﹣2) .
【分析】(1)把10分解成2×5;
(2)把﹣3分解成﹣3×1;
(3)把12分解成(﹣3)×(﹣4);
(4)把﹣18分解成(﹣2)×9;
【解答】(1)x2+7x+10=(x+2)(x+5);
(2)x2﹣2x﹣3=(x﹣3)(x+1);
(3)y2﹣7y+12=(y﹣3)(y﹣4);
(4)x2+7x﹣18=(x+9)(x﹣2).
故答案为:(1)(x+2)(x+5),(2)(x﹣3)(x+1),(3)(y﹣3)(y﹣4),(4)(x+9)(x﹣2).
【点评】本题主要考查了因式分解﹣十字相乘法,熟练掌握十字相乘法分解因式的方法,根据题意可知a、b是相互独立的,利用多项式相乘法则计算,再根据对应系数相等即可求出a、b的值,是解题关键.
22.如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示,设点B所表示的数为m.
(1)实数m的值是 2﹣ .
(2)求|m+1|+|m﹣1|的值;
(3)在数轴上还有C、D两点分别表示实数c和d,且有|2c+4|与互为相反数,求2c+3d的平方根.
【分析】(1)通过A,B在数轴上表示的数进行运算.
(2)化简绝对值进行运算.
(3)根据非负数的意义进行解答.
【解答】解:∵点B在点A右侧2个单位处,
∴点B所表示的数m为:﹣+2,即2﹣.
故答案为:2﹣.
,则m+1>0,m﹣1<0,
∴|m+1|+|m﹣1|=m+1+1﹣m=2;
答:|m+1|+|m﹣1|的值为2.
(3)∵|2c+4|与互为相反数,
∴,
∴|2c+4|=0,且,
解得:c=﹣2,d=4,
∴2c+3d=8,
∴2c+3d的平方根为±2.
答:2c+3d的平方根为±2.
【点评】本题考查数轴,非负数及二次根式的运算,解题关键是熟练掌握绝对值与平方根的意义.
23.如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①x﹣(3x+1)=﹣5;②+1=0;③3x﹣1=0中,不等式组的关联方程是 ① (填序号).
(2)若不等式组的某个关联方程的根是整数,则这个关联方程可以是 x﹣2=0 (写出一个即可)
(3)若方程﹣x=x,3+x=2(x+)都是关于x的不等式组的关联方程,直接写出m的取值范围.
【分析】(1)根据关联方程的定义可以解答本题;
(2)本题答案不唯一,写出的方程只要符合题意即可;
(3)根据题意可以求得m的取值范围.
【解答】解:(1)由不等式组得,,
由x﹣(3x+1)=﹣5,解得,x=2,故方程①x﹣(3x+1)=﹣5是不等式组的关联方程,
由+1=0得,x=,故方程②+1=0不是不等式组的关联方程,
由3x﹣1=0,得x=,故方程③3x﹣1=0不是不等式组的关联方程,
故答案为:①;
(2)由不等式组,解得,0.5<x<3,则它的关联方程的根是整数是一个方程是x﹣2=0,
故答案为:x﹣2=0;
(3)由﹣x=x,得x=0.5,由3+x=2(x+)得x=2,
由不等式组,解得,m<x≤2+m,
∵方程﹣x=x,3+x=2(x+)都是关于x的不等式组的关联方程,
∴,得0≤m<0.5,
即m的取值范围是0≤m<0.5.
【点评】本题考查解一元一次不等式组、一元一次方程的解,解答本题的关键是明确题意,利用方程和不等式的知识解答
考试时间:120分钟
一、选择题(每小题4分,共40分)
1.下列数中,是无理数的是( )
A. B.
C.﹣2.171171117 D.
2.下列运算正确的是( )
A.=±2 B.(﹣3)3=27 C.=3 D.=2
3.若a<b,c≠0,则下列不等式不一定成立的是( )
A.a+c<b+c B.a﹣c<b﹣c C.ac2<bc2 D.<
4.估计﹣1的值在( )
A.2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
5.下列运算正确的是( )
A.2a﹣a=2 B.(a﹣1)2=a2﹣1
C.(2a3)2=4a6 D.a6÷a3=a2
6.已知2a=5,2b=10,2c=50,那么a、b、c之间满足的等量关系是( )
A.ab=c B.a+b=c
C.a:b:c=1:2:10 D.a2b2=c2
7.不等式2(1﹣2x)≤12﹣6x最大整数解是的解,则a的值是( )
A. B. C.0 D.﹣2
8.某学校准备购进单价分别为5元和7元的A、B两种笔记本共50本作为奖品发放给学生,要求A种笔记本的数量不多于B种笔记本数量的3倍,不少于B种笔记本数量的2倍,则不同的购买方案种数为( )
A.1 B.2 C.3 D.4
9.已知a1为实数,规定运算:,,,,…,an=1﹣.按上述方法计算:当a1=3时,a2022的值等于( )
A. B. C. D.
10.如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
二、填空题(共4小题,共计20分)
11.因式分解:3x﹣12x3= .
12.若一个正数m的两个平方根分别是3a+2和a﹣10,则m的立方根为 .
13.如图,边长为a+3的正方形纸片剪出一个边长为a的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为3,则另一边长为 .
14.已知关于x的不等式组恰好有2个整数解,则a的取值范围是 .
解答题(共9小题。15-18每题8分,19-20每题10分,21-22每题12分,23题14分,共计60分)
15.计算:+++.
16.计算:(﹣a2)3÷a2+(a+2)(a2﹣2a+4).
17.解不等式组,并把不等式组的解集在数轴上表示出来.
18.已知3m=4,3n=5,分别求3m+n与32m﹣n的值.
19.如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 ;(请选择正确的选项)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= .
②计算:(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).
20.截至12月25日,全国累计报告接种新型冠状病毒疫苗超过12亿剂次.为了满足市场需求,某公司计划投入10个大、小两种车间共同生产同一种新型冠状病毒疫苗,已知1个大车间和2个小车间每周能生产疫苗共35万剂,2个大车间和1个小车间每周能生产疫苗共40万剂,每个大车间生产1万剂疫苗的平均成本为90万元,每个小车间生产1方剂疫苗的平均成本为80万元.
(1)该公司每个大车间、小车间每周分别能生产疫苗多少万剂?
(2)若投入的10个车间每周生产的疫苗不少于135万剂,请问一共有几种投入方案,并求出每周生产疫苗的总成本最小值?
21.阅读材料:根据多项式乘多项式法则,我们很容易计算:
(x+2)(x+3)=x2+5x+6;(x﹣1)(x+3)=x2+2x﹣3.
而因式分解是与整式乘法方向相反的变形,利用这种关系可得:
x2+5x+6=(x+2)(x+3);x2+2x﹣3=(x﹣1)(x+3).
通过这样的关系我们可以将某些二次项系数是1的二次三项式分解因式.如将式子x2+2x﹣3分解因式.这个式子的二次项系数是1=1×1,常数项﹣3=(﹣1)×3,一次项系数2=(﹣1)+3,可以用下图十字相乘的形式表示为:
先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求和,使其等于一次项系数,然后横向书写.这样,我们就可以得到:x2+2x﹣3=(x﹣1)(x+3).
利用这种方法,将下列多项式分解因式:
(1)x2+7x+10= ;
(2)x2﹣2x﹣3= ;
(3)y2﹣7y+12= ;
(4)x2+7x﹣18= .
22.如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示,设点B所表示的数为m.
(1)实数m的值是 .
(2)求|m+1|+|m﹣1|的值;
(3)在数轴上还有C、D两点分别表示实数c和d,且有|2c+4|与互为相反数,求2c+3d的平方根.
23.如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①x﹣(3x+1)=﹣5;②+1=0;③3x﹣1=0中,不等式组的关联方程是 (填序号).
(2)若不等式组的某个关联方程的根是整数,则这个关联方程可以是 (写出一个即可)
(3)若方程﹣x=x,3+x=2(x+)都是关于x的不等式组的关联方程,直接写出m的取值范围.
2021-2022学年沪科版七年级数学下册期中测试卷(安徽专版)
考试时间:120分钟
选择题(每小题4分,共40分)
1.下列数中,是无理数的是( )
A. B.
C.﹣2.171171117 D.
【分析】理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】解:A.是分数,属于有理数,故本选项不合题意;
B.,是整数,属于有理数,故本选项不合题意;
C.﹣2.171171117是有限小数,属于有理数,故本选项不合题意;
D.是无理数,故本选项符合题意.
故选:D.
【点评】本题主要考查了无理数.解题的关键是掌握无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
2.下列运算正确的是( )
A.=±2 B.(﹣3)3=27 C.=3 D.=2
【分析】根据算术平方根、立方根、有理数的乘方的定义解决此题.
【解答】解:A.根据算术平方根的定义,,那么A错误,故A不符合题意.
B.根据有理数的乘方,(﹣3)3=﹣27,那么B错误,故B不符合题意.
C.根据立方根的定义,,那么C错误,故C不符合题意.
D.根据算术平方根的定义,,那么D正确,故D符合题意.
故选:D.
【点评】本题主要考查算术平方根、立方根、有理数的乘方,熟练掌握算术平方根、立方根、有理数的乘方的定义是解决本题的关键.
3.若a<b,c≠0,则下列不等式不一定成立的是( )
A.a+c<b+c B.a﹣c<b﹣c C.ac2<bc2 D.<
【分析】根据不等式的基本性质判断即可.
【解答】解:A选项,∵a<b,
∴a+c<b+c,故该选项不符合题意;
B选项,∵a<b,
∴a﹣c<b﹣c,故该选项不符合题意;
C选项,∵a<b,c≠0,
∴ac2<bc2,故该选项不符合题意;
D选项,∵a<b,c≠0,
∴当c>0时,<;
当c<0时,>,故该选项符合题意;
故选:D.
【点评】本题考查了不等式的基本性质,掌握①不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变;②不等式的两边同时乘(或除以)同一个正数,不等号的方向不变;③不等式的两边同时乘(或除以)同一个负数,不等号的方向改变是解题的关键.
4.估计﹣1的值在( )
A.2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
【分析】估算出的值进行计算即可解答.
【解答】解:∵25<26<36,
∴5<<6,
∴4<﹣1<5,
∴估计﹣1的值在:4到5之间,
故选:C.
【点评】本题考查了估算无理数的大小,熟练掌握平方数是解题的关键.
5.下列运算正确的是( )
A.2a﹣a=2 B.(a﹣1)2=a2﹣1
C.(2a3)2=4a6 D.a6÷a3=a2
【分析】根据合并同类项法则、完全平方公式、积的乘方与幂的乘方法法则、同底数幂的除法法则解决此题.
【解答】解:A.根据合并同类项法则,2a﹣a=a,那么A错误,故A不符合题意.
B.根据完全平方公式,(a﹣1)2=a2+1﹣2a,那么B错误,故B不符合题意.
C.根据积的乘方与幂的乘方,(2a3)2=4a6,那么C正确,故C符合题意.
D.根据同底数幂的除法,a6÷a3=a3,那么D错误,故D不符合题意.
故选:C.
【点评】本题主要考查合并同类项、完全平方公式、积的乘方与幂的乘方、同底数幂的除法,熟练掌握合并同类项法则、完全平方公式、积的乘方与幂的乘方、同底数幂的除法法则是解决本题的关键.
6.已知2a=5,2b=10,2c=50,那么a、b、c之间满足的等量关系是( )
A.ab=c B.a+b=c
C.a:b:c=1:2:10 D.a2b2=c2
【分析】根据5×10=50,得到2a 2b=2c,根据同底数幂的乘法法则得到2a+b=2c,从而a+b=c.
【解答】解:∵5×10=50,
∴2a 2b=2c,
∴2a+b=2c,
∴a+b=c,
故选:B.
【点评】本题考查了同底数幂的乘法,掌握am an=am+n是解题的关键.
7.不等式2(1﹣2x)≤12﹣6x最大整数解是的解,则a的值是( )
A. B. C.0 D.﹣2
【分析】根据不等式2(1﹣2x)≤12﹣6x求得x的最大整数解,代入是,即可求得a的值.
【解答】解:2(1﹣2x)≤12﹣6x,
2﹣4x≤12﹣6x,
6x﹣4x≤12﹣2,
2x≤10,
x≤5,
∴不等式2(1﹣2x)≤12﹣6x最大整数解是5,
把x=5代入得,﹣5=,
∴=5,
∴a=,
故选:B.
【点评】本题考查了一元一次不等式的整数解,一元一次方程的解,通过解不等式求得不等式的最大整数解是解题的关键.
8.某学校准备购进单价分别为5元和7元的A、B两种笔记本共50本作为奖品发放给学生,要求A种笔记本的数量不多于B种笔记本数量的3倍,不少于B种笔记本数量的2倍,则不同的购买方案种数为( )
A.1 B.2 C.3 D.4
【分析】设购进A种笔记本为x本,则购进B种笔记本为(50﹣x)本,由题意:A种笔记本的数量不多于B种笔记本数量的3倍,不少于B种笔记本数量的2倍,列出不等式组,解不等式组,取正整数解即可.
【解答】解:设购进A种笔记本为x本,则购进B种笔记本为(50﹣x)本,
由题意得:,
解得:33≤x≤37,
∵x为正整数,
∴x的取值为34,、35、36、37,
则不同的购买方案种数为4种,
故选:D.
【点评】本题考查了一元一次不等式组的应用,找出数量关系,列出一元一次不等式组是解题的关键.
9.已知a1为实数,规定运算:,,,,…,an=1﹣.按上述方法计算:当a1=3时,a2022的值等于( )
A. B. C. D.
【分析】把a1=3代入进行计算,找出规律即可解答.
【解答】解:a1=3,
a2=1﹣=1﹣=,
a3=1﹣=1﹣=,
a4=1﹣=1﹣=3,
...
∴2022÷3=674,
∴a2022=,
故选:C.
【点评】本题考查了实数的运算,规律型:数字变化类,把a1=3代入进行计算从数字找规律是解题的关键.
10.如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
【分析】由图可得阴影部分面积为4个直角三角形面积的和.
【解答】解:如图,
∵a﹣b=2,ab=26,
∴a2﹣2ab+b2=4,
∴a2+b2=4+2ab=4+52=56,
阴影部分的面积=S△ABC+S△CDM+S△AEF+S△GHM
=2×(a﹣b)×a+2×b×b
=a(a﹣b)+b2
=a2+b2﹣ab
=56﹣26
=30.
故选:A.
【点评】本题主要考查了完全平方公式的几何背景的应用,根据题意列出阴影部分面积的表达式是解决本题的关键.
二.填空题(共4小题)
11.因式分解:3x﹣12x3= 3x(1+2x)(1﹣2x) .
【分析】先提公因式,然后利用平方差公式继续分解即可.
【解答】解:3x﹣12x3
=3x(1﹣4x2)
=3x(1+2x)(1﹣2x),
故答案为:3x(1+2x)(1﹣2x).
【点评】本题考查了提公因式法与公式法的综合运用,一定要注意如果多项式的各项含有公因式,必须先提公因式.
12.若一个正数m的两个平方根分别是3a+2和a﹣10,则m的立方根为 4 .
【分析】根据平方根的性质以及立方根的定义解决此题.
【解答】解:由题意得,3a+2+a﹣10=0.
∴a=2.
∴3a+2=8.
∴m=64.
∴m的立方根为4.
故答案为:4.
【点评】本题主要考查平方根、立方根,熟练掌握平方根的性质、立方根的定义是解决本题的关键.
13.如图,边长为a+3的正方形纸片剪出一个边长为a的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为3,则另一边长为 2a+3 .
【分析】根据拼图中各个部分之间的关系得出答案.
【解答】解:如图,将剩余部分拼成一个长方形.这个长方形一边长为3,另一边长为a+(a+3),
即2a+3,
故答案为:2a+3.
【点评】本题考查平方差公式的几何背景,理解拼图中各个部分之间的关系是解决问题的关键.
14.已知关于x的不等式组恰好有2个整数解,则a的取值范围是 ﹣4<a≤﹣2 .
【分析】先求出不等式组的解集,根据不等式组有2个整数解得出1≤﹣<2,再求出a的范围即可.
【解答】解:,
解不等式①,得x>﹣,
解不等式②,得x<4,
所以不等式组的解集是﹣<x<4,
∵关于x的不等式组恰好有2个整数解(整数解是2,3),
∴1≤﹣<2,
解得:﹣4<a≤﹣2,
故答案为:﹣4<a≤﹣2.
【点评】本题考查了解一元一次不等式组和不等式组的整数解,能得出关于a的不等式组是解此题的关键.
三.解答题(共9小题)
15.计算:+++.
【分析】先计算绝对值和开方,再计算加减即可.
【解答】解:+++
=﹣2+5+2﹣3
=+2.
【点评】此题考查了绝对值、开方及加减混合运算能力,关键是能确定正确的运算顺序和能对以上知识熟练准确计算.
16.计算:(﹣a2)3÷a2+(a+2)(a2﹣2a+4).
【分析】根据多项式乘多项式、幂的乘方与积的乘方以及同底数幂的除法法则分别进行计算,即可得出答案.
【解答】解:(﹣a2)3÷a2+(a+2)(a2﹣2a+4)
=﹣a6÷a2+a3﹣2a2+4a+2a2﹣4a+8
=﹣a4+a3﹣2a2+4a+2a2﹣4a+8
=﹣a4+a3+8.
【点评】此题考查了多项式乘多项式、幂的乘方与积的乘方以及同底数幂的除法,熟练掌握运算法则是解题的关键.
17.解不等式组,并把不等式组的解集在数轴上表示出来.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【解答】解:解不等式2x+1<3x+3,得:x>﹣2,
解不等式x+≤,得:x≤0.5,
则不等式组的解集为﹣2<x≤0.5,
将不等式组的解集表示在数轴上如下:
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
18.已知3m=4,3n=5,分别求3m+n与32m﹣n的值.
【分析】利用同底数幂的乘法的法则,同底数幂的除法的法则,幂的乘方的法则对所求的式子进行整理,再代入运算即可.
【解答】解:当3m=4,3n=5时,
3m+n
=3m×3n
=4×5
=20;
32m﹣n
=32m÷3n
=(3m)2÷3n
=42÷5
=16÷5
=.
【点评】本题主要考查同底数幂的除法,同底数幂的乘法,幂的乘方,解答的关键是对相应的运算法则的掌握.
19.如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 A ;(请选择正确的选项)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= 4 .
②计算:(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).
【分析】(1)用两种方法表示阴影部分的面积即可.
(2)利用(1)中得到的平方差公式计算.
【解答】解:(1)图1中阴影部分的面积=a2﹣b2,图②中阴影部分的面积=(a+b)(a﹣b).
∴a2﹣b2=(a+b)(a﹣b).
故选A.
(2)①∵(2a+b)(2a﹣b)=4a2﹣b2.
∴6(2a﹣b)=24,
∴2a﹣b=24÷6=4.
故答案为:4.
②=
=
=
=.
【点评】本题考查平方差公式及其应用,用两种方法表示同一个图形面积,再用所得公式完成计算是求解本题的关键.
20.截至12月25日,全国累计报告接种新型冠状病毒疫苗超过12亿剂次.为了满足市场需求,某公司计划投入10个大、小两种车间共同生产同一种新型冠状病毒疫苗,已知1个大车间和2个小车间每周能生产疫苗共35万剂,2个大车间和1个小车间每周能生产疫苗共40万剂,每个大车间生产1万剂疫苗的平均成本为90万元,每个小车间生产1方剂疫苗的平均成本为80万元.
(1)该公司每个大车间、小车间每周分别能生产疫苗多少万剂?
(2)若投入的10个车间每周生产的疫苗不少于135万剂,请问一共有几种投入方案,并求出每周生产疫苗的总成本最小值?
【分析】(1)设该公司每个大车间每周能生产疫苗x万剂,每个小车间每周能生产疫苗y万剂,根据“1个大车间和2个小车间每周能生产疫苗共35万剂,2个大车间和1个小车间每周能生产疫苗共40方剂”,即可得出关于x,y的二元一次方程组,解之即可求出该公司每个大车间、小车间每周生产疫苗的数量;
(2)设投入m个大车间,则投入小车间(10﹣m)个,根据每周生产的疫苗不少于135万剂,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,结合m,(10﹣m)均为正整数,即可得出投入方案的个数,再求出各投入方案每周生产疫苗的总成本,比较后即可得出每周生产疫苗的总成本最小值为11850万元.
【解答】解:(1)设该公司每个大车间每周能生产疫苗x万剂,每个小车间每周能生产疫苗y万剂,
依题意得:,
解得:.
答:该公司每个大车间每周能生产疫苗15万剂,每个小车间每周能生产疫苗10万剂.
(2)设投入m个大车间,则投入小车间(10﹣m)个,
依题意得:15m+10(10﹣m)≥135,
解得:m≥7.
又∵m,(10﹣m)均为正整数,
∴m可以为7,8,9,
∴共有3种投入方案,
方案1:投入7个大车间,3个小车间,每周生产疫苗的总成本90×15×7+80×10×3=11850(万元);
方案2:投入8个大车间,2个小车间,每周生产疫苗的总成本90×15×8+80×10×2=12400(万元);
方案3:投入9个大车间,1个小车间,每周生产疫苗的总成本90×15×9+80×10×1=12950(万元).
∵11850<12400<12950,
∴一共有3种投入方案,每周生产疫苗的总成本最小值为11850万元.
【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
21.阅读材料:根据多项式乘多项式法则,我们很容易计算:
(x+2)(x+3)=x2+5x+6;(x﹣1)(x+3)=x2+2x﹣3.
而因式分解是与整式乘法方向相反的变形,利用这种关系可得:
x2+5x+6=(x+2)(x+3);x2+2x﹣3=(x﹣1)(x+3).
通过这样的关系我们可以将某些二次项系数是1的二次三项式分解因式.如将式子x2+2x﹣3分解因式.这个式子的二次项系数是1=1×1,常数项﹣3=(﹣1)×3,一次项系数2=(﹣1)+3,可以用下图十字相乘的形式表示为:
先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求和,使其等于一次项系数,然后横向书写.这样,我们就可以得到:x2+2x﹣3=(x﹣1)(x+3).
利用这种方法,将下列多项式分解因式:
(1)x2+7x+10= (x+2)(x+5) ;
(2)x2﹣2x﹣3= (x﹣3)(x+1) ;
(3)y2﹣7y+12= (y﹣3)(y﹣4) ;
(4)x2+7x﹣18= (x+9)(x﹣2) .
【分析】(1)把10分解成2×5;
(2)把﹣3分解成﹣3×1;
(3)把12分解成(﹣3)×(﹣4);
(4)把﹣18分解成(﹣2)×9;
【解答】(1)x2+7x+10=(x+2)(x+5);
(2)x2﹣2x﹣3=(x﹣3)(x+1);
(3)y2﹣7y+12=(y﹣3)(y﹣4);
(4)x2+7x﹣18=(x+9)(x﹣2).
故答案为:(1)(x+2)(x+5),(2)(x﹣3)(x+1),(3)(y﹣3)(y﹣4),(4)(x+9)(x﹣2).
【点评】本题主要考查了因式分解﹣十字相乘法,熟练掌握十字相乘法分解因式的方法,根据题意可知a、b是相互独立的,利用多项式相乘法则计算,再根据对应系数相等即可求出a、b的值,是解题关键.
22.如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示,设点B所表示的数为m.
(1)实数m的值是 2﹣ .
(2)求|m+1|+|m﹣1|的值;
(3)在数轴上还有C、D两点分别表示实数c和d,且有|2c+4|与互为相反数,求2c+3d的平方根.
【分析】(1)通过A,B在数轴上表示的数进行运算.
(2)化简绝对值进行运算.
(3)根据非负数的意义进行解答.
【解答】解:∵点B在点A右侧2个单位处,
∴点B所表示的数m为:﹣+2,即2﹣.
故答案为:2﹣.
,则m+1>0,m﹣1<0,
∴|m+1|+|m﹣1|=m+1+1﹣m=2;
答:|m+1|+|m﹣1|的值为2.
(3)∵|2c+4|与互为相反数,
∴,
∴|2c+4|=0,且,
解得:c=﹣2,d=4,
∴2c+3d=8,
∴2c+3d的平方根为±2.
答:2c+3d的平方根为±2.
【点评】本题考查数轴,非负数及二次根式的运算,解题关键是熟练掌握绝对值与平方根的意义.
23.如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①x﹣(3x+1)=﹣5;②+1=0;③3x﹣1=0中,不等式组的关联方程是 ① (填序号).
(2)若不等式组的某个关联方程的根是整数,则这个关联方程可以是 x﹣2=0 (写出一个即可)
(3)若方程﹣x=x,3+x=2(x+)都是关于x的不等式组的关联方程,直接写出m的取值范围.
【分析】(1)根据关联方程的定义可以解答本题;
(2)本题答案不唯一,写出的方程只要符合题意即可;
(3)根据题意可以求得m的取值范围.
【解答】解:(1)由不等式组得,,
由x﹣(3x+1)=﹣5,解得,x=2,故方程①x﹣(3x+1)=﹣5是不等式组的关联方程,
由+1=0得,x=,故方程②+1=0不是不等式组的关联方程,
由3x﹣1=0,得x=,故方程③3x﹣1=0不是不等式组的关联方程,
故答案为:①;
(2)由不等式组,解得,0.5<x<3,则它的关联方程的根是整数是一个方程是x﹣2=0,
故答案为:x﹣2=0;
(3)由﹣x=x,得x=0.5,由3+x=2(x+)得x=2,
由不等式组,解得,m<x≤2+m,
∵方程﹣x=x,3+x=2(x+)都是关于x的不等式组的关联方程,
∴,得0≤m<0.5,
即m的取值范围是0≤m<0.5.
【点评】本题考查解一元一次不等式组、一元一次方程的解,解答本题的关键是明确题意,利用方程和不等式的知识解答
同课章节目录
