甘肃省河西五市部分普通高中2013年1月高三第一次联合考试理科数学试卷
文档属性
| 名称 | 甘肃省河西五市部分普通高中2013年1月高三第一次联合考试理科数学试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 138.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-01 00:00:00 | ||
图片预览



文档简介
甘肃省河西五市部分普通高中2013年1月高三第一次联合考试
数学试题(理科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,其中第II卷第(22)-(24)题为选考题,其他题为必考题。考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
参考公式:
锥体体积公式 ,其中为底面面积,为高;
柱体体积公式 其中为底面面积,为高;
球的表面积,体积公式 ,,其中R为球的半径。
第Ⅰ卷
选择题(共12小题,每题5分,总分60分)
1.已知复数
A. 2 B. -2 C. D.
2.设集合M={x∣x<2},集合N={x∣0 A. M∪N=R B. M∪СRN=R C. N∪СRM=R D. M∩N=M
3.下列命题中,是真命题的是( )
A. B.
C. D.
4.函数( )
A. B. C. D.
5.已知函数( )
A. B. C. D.
6.若对恒成立,则三角形ABC是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定形状的三角形
7.已知双曲线的右焦点是F, 过点F且倾角为600的直线与双曲线的右支有且只有一个交点,则此双曲线的离心率的范围是( )
A. B. (1,2) C. D.
8.若函数对称,那么=( )
A. B.- C. 1 D. -1
9.一空间几何体的三视图如图1,则该几何体的体积为( )
A. B.
C. D.
10.已知O是坐标原点,,若点为平面区域上一动点,则的取值范围是( )
A. B. C. D.
11.已知三棱柱的侧棱与底面边长都相等,在底面内的射影为的中心,则与底面所成角的正弦值等于( )
A. B. C. D.
12.已知圆C:,从动圆M:上的动点P向圆C引切线,切点分别是E,F,则( )
A. B. C. D.
第Ⅱ卷
填空题(共4小题,每题5分,总分20分)
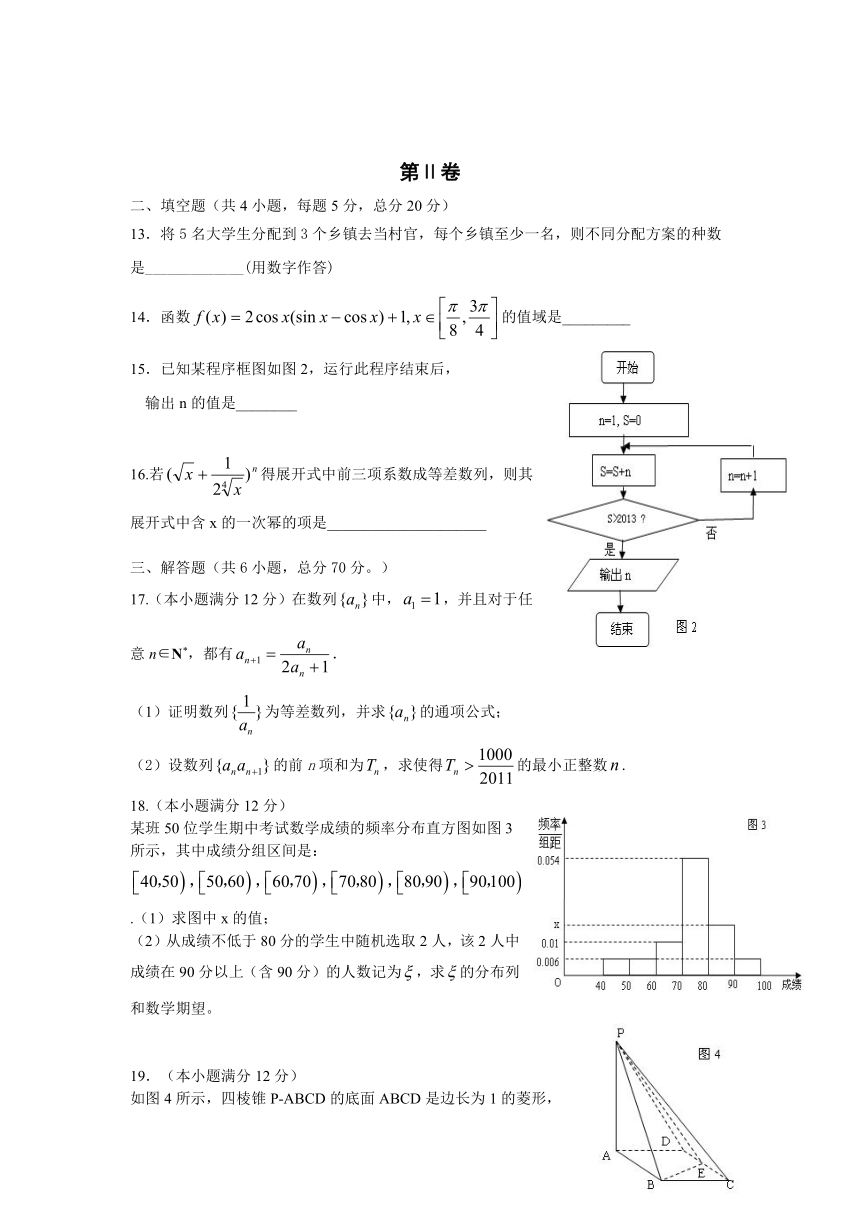
13.将5名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同分配方案的种数
是_____________(用数字作答)
14.函数的值域是_________
15.已知某程序框图如图2,运行此程序结束后,
输出n的值是________
16.若得展开式中前三项系数成等差数列,则其展开式中含x的一次幂的项是_____________________
三、解答题(共6小题,总分70分。)
17.(本小题满分12分)在数列中,,并且对于任意n∈N*,都有.
(1)证明数列为等差数列,并求的通项公式;
(2)设数列的前n项和为,求使得的最小正整数.
18.(本小题满分12分)
某班50位学生期中考试数学成绩的频率分布直方图如图3所示,其中成绩分组区间是:.(1)求图中x的值;
(2)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为,求的分布列和数学期望。
19.(本小题满分12分)
如图4所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,BCD=60,E是CD的中点,PA底面ABCD,PA=2.
(1)证明:平面PBE平面PAB;
(2)求平面PAD和平面PBE所成二面角的正弦值。
20.(本小题满分12分)
抛物线的顶点在原点,焦点在x轴的正半轴上,直线x+y-1=0与抛物线相交于A、B两点,
且。
(1) 求抛物线方程;
(2) 在x轴上是否存在一点C,使得三角形ABC是正三角形? 若存在,求出点C的坐标,若不存在,说明理由.
21.(本小题满分12分)设函数
若;
若
请考生在22,23,24三题中任选一题作答,如果多做,则按所做的第一题计分。做答时标出所选题目的题号。
22.(本小题满分10分)选修4-1;几何证明选讲
如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,
AC⊥BD,E是DC中点
连结EM交AB于F,作OH⊥AB于H,
求证:(1)EF⊥AB (2)OH=ME
23. 本小题满分10分)选修4-4;坐标系与参数方程
已知直线l经过点P(,1),倾斜角,在极坐标系下,圆C的极坐标方程为。
(1)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(2)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积。
24.(本小题满分10分)选修4-5;不等式选讲
(1)解不等式
(2)设x,y,z且,求的最小值.
2013年1月甘肃省河西五市部分普通高中高三第一次联合考试
数学试题(理科) 参考答案
第Ⅰ卷
一、选择题
ABCCB BCDCC BA
第Ⅱ卷
二、填空题
13 150 14 15 63 16
17. 解:(1),因为,所以,
∴ 数列是首项为1,公差为2的等差数列,
∴ ,从而 …………………………………………6分
(2) 因为
所以
,
由,
得,
最小正整数为91.………………………………………………12分
18.(1)
得x=0.018 ………………………………………………………4分
(2)由已知得,不低于80分的学生为12人,90分以上为3人,随机变量
的可能取值是0,1,2
………………………………………………10分
E=…=………………………………………………12分
19(1)略……………………………………………………………………5分
(2)延长AD,BE相交于F,联结PF,过A作AH⊥PB于H,
平面PBE平面PAB知,AH平面PBE,
过H作HGPF于联结AG,
则∠AGH为所求锐二面角的平面角……………………………8分
计算略
sin∠AGH=…………………………………………………12分
法2 向量法(略)
20.(1)设抛物线方程为
得:
设
则
抛物线方程是……………………………………………6分
(2)设AB的中点是D,则
假设x轴上存在一点C(x0, 0)
因为三角形是正三角形,
所以CD⊥AB
得:
又
矛盾,故在x轴上不存在一点C, 使三角形ABC是正三角形…………12分
21.(1)
… …
………………………4分
(2)
因为
(i)当
上是增函数,
此时 恒成立…………………………………………8分
(ii)当,
令,
易得
这与已知相悖
综上所述:………………12分
22 (1)
……………………………………………………………………5分
(2)
连结HM,并延长交CD于G,又(1)的证法,可证
∴OE∥HG ,OH∥EF
∴OEMH是平行四边形
∴OH=ME…………………………………………………………………10分
23.(1)直线L参数方程是
圆的普通方程是………………………5分
(2)又代入得:
…………………………………………10分
24.(1)……………………………………………5分
(2)…………………10分
注:考生未指出等号成立的条件,应扣2分
数学试题(理科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,其中第II卷第(22)-(24)题为选考题,其他题为必考题。考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
参考公式:
锥体体积公式 ,其中为底面面积,为高;
柱体体积公式 其中为底面面积,为高;
球的表面积,体积公式 ,,其中R为球的半径。
第Ⅰ卷
选择题(共12小题,每题5分,总分60分)
1.已知复数
A. 2 B. -2 C. D.
2.设集合M={x∣x<2},集合N={x∣0
3.下列命题中,是真命题的是( )
A. B.
C. D.
4.函数( )
A. B. C. D.
5.已知函数( )
A. B. C. D.
6.若对恒成立,则三角形ABC是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定形状的三角形
7.已知双曲线的右焦点是F, 过点F且倾角为600的直线与双曲线的右支有且只有一个交点,则此双曲线的离心率的范围是( )
A. B. (1,2) C. D.
8.若函数对称,那么=( )
A. B.- C. 1 D. -1
9.一空间几何体的三视图如图1,则该几何体的体积为( )
A. B.
C. D.
10.已知O是坐标原点,,若点为平面区域上一动点,则的取值范围是( )
A. B. C. D.
11.已知三棱柱的侧棱与底面边长都相等,在底面内的射影为的中心,则与底面所成角的正弦值等于( )
A. B. C. D.
12.已知圆C:,从动圆M:上的动点P向圆C引切线,切点分别是E,F,则( )
A. B. C. D.
第Ⅱ卷
填空题(共4小题,每题5分,总分20分)
13.将5名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同分配方案的种数
是_____________(用数字作答)
14.函数的值域是_________
15.已知某程序框图如图2,运行此程序结束后,
输出n的值是________
16.若得展开式中前三项系数成等差数列,则其展开式中含x的一次幂的项是_____________________
三、解答题(共6小题,总分70分。)
17.(本小题满分12分)在数列中,,并且对于任意n∈N*,都有.
(1)证明数列为等差数列,并求的通项公式;
(2)设数列的前n项和为,求使得的最小正整数.
18.(本小题满分12分)
某班50位学生期中考试数学成绩的频率分布直方图如图3所示,其中成绩分组区间是:.(1)求图中x的值;
(2)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为,求的分布列和数学期望。
19.(本小题满分12分)
如图4所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,BCD=60,E是CD的中点,PA底面ABCD,PA=2.
(1)证明:平面PBE平面PAB;
(2)求平面PAD和平面PBE所成二面角的正弦值。
20.(本小题满分12分)
抛物线的顶点在原点,焦点在x轴的正半轴上,直线x+y-1=0与抛物线相交于A、B两点,
且。
(1) 求抛物线方程;
(2) 在x轴上是否存在一点C,使得三角形ABC是正三角形? 若存在,求出点C的坐标,若不存在,说明理由.
21.(本小题满分12分)设函数
若;
若
请考生在22,23,24三题中任选一题作答,如果多做,则按所做的第一题计分。做答时标出所选题目的题号。
22.(本小题满分10分)选修4-1;几何证明选讲
如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,
AC⊥BD,E是DC中点
连结EM交AB于F,作OH⊥AB于H,
求证:(1)EF⊥AB (2)OH=ME
23. 本小题满分10分)选修4-4;坐标系与参数方程
已知直线l经过点P(,1),倾斜角,在极坐标系下,圆C的极坐标方程为。
(1)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(2)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积。
24.(本小题满分10分)选修4-5;不等式选讲
(1)解不等式
(2)设x,y,z且,求的最小值.
2013年1月甘肃省河西五市部分普通高中高三第一次联合考试
数学试题(理科) 参考答案
第Ⅰ卷
一、选择题
ABCCB BCDCC BA
第Ⅱ卷
二、填空题
13 150 14 15 63 16
17. 解:(1),因为,所以,
∴ 数列是首项为1,公差为2的等差数列,
∴ ,从而 …………………………………………6分
(2) 因为
所以
,
由,
得,
最小正整数为91.………………………………………………12分
18.(1)
得x=0.018 ………………………………………………………4分
(2)由已知得,不低于80分的学生为12人,90分以上为3人,随机变量
的可能取值是0,1,2
………………………………………………10分
E=…=………………………………………………12分
19(1)略……………………………………………………………………5分
(2)延长AD,BE相交于F,联结PF,过A作AH⊥PB于H,
平面PBE平面PAB知,AH平面PBE,
过H作HGPF于联结AG,
则∠AGH为所求锐二面角的平面角……………………………8分
计算略
sin∠AGH=…………………………………………………12分
法2 向量法(略)
20.(1)设抛物线方程为
得:
设
则
抛物线方程是……………………………………………6分
(2)设AB的中点是D,则
假设x轴上存在一点C(x0, 0)
因为三角形是正三角形,
所以CD⊥AB
得:
又
矛盾,故在x轴上不存在一点C, 使三角形ABC是正三角形…………12分
21.(1)
… …
………………………4分
(2)
因为
(i)当
上是增函数,
此时 恒成立…………………………………………8分
(ii)当,
令,
易得
这与已知相悖
综上所述:………………12分
22 (1)
……………………………………………………………………5分
(2)
连结HM,并延长交CD于G,又(1)的证法,可证
∴OE∥HG ,OH∥EF
∴OEMH是平行四边形
∴OH=ME…………………………………………………………………10分
23.(1)直线L参数方程是
圆的普通方程是………………………5分
(2)又代入得:
…………………………………………10分
24.(1)……………………………………………5分
(2)…………………10分
注:考生未指出等号成立的条件,应扣2分
同课章节目录
