山东省临沂市重点高中2012-2013学年高二上学期期末考试 理科数学 Word版含答案
文档属性
| 名称 | 山东省临沂市重点高中2012-2013学年高二上学期期末考试 理科数学 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 181.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-01 11:59:08 | ||
图片预览



文档简介
2012—2013学年度上学期期末模块质量调研试题
高二(理)数学 2013. 1
注意事项:
1.答题前,请先将自己的姓名、考场、考号在卷首的相应位置填写清楚;
2.选择题答案涂在答题卡上,非选择题用蓝色、黑色钢笔或圆珠笔直接写在试卷上
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的).
1.在中,角所对的边分别是,且,则
A. B. C. D.
2.抛物线焦点坐标是
A.(,0) B.(,0) C. (0, ) D.(0, )
3.“”是“”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.椭圆与双曲线有相同的焦点,则的值是
A. B.1或-2 C.1或 D.1
5.若A,B,当取最小值时,的值为
A.6 B.3 C.2 D.1
6.下列命题中为真命题的是
①“若,则不全为零”的否命题; ②“等腰三角形都相似”的逆命题; ③“若,则不等式的解集为R”的逆否命题。
A.① B.①③ C.②③ D.①②③
7. 设成等比数列,其公比为2,则的值为
A.1 B. C. D.
8.设A是△ABC中的最小角,且,则实数a的取值范围是
A.a≥3 B.a>-1 C.-1<a≤3 D.a>0
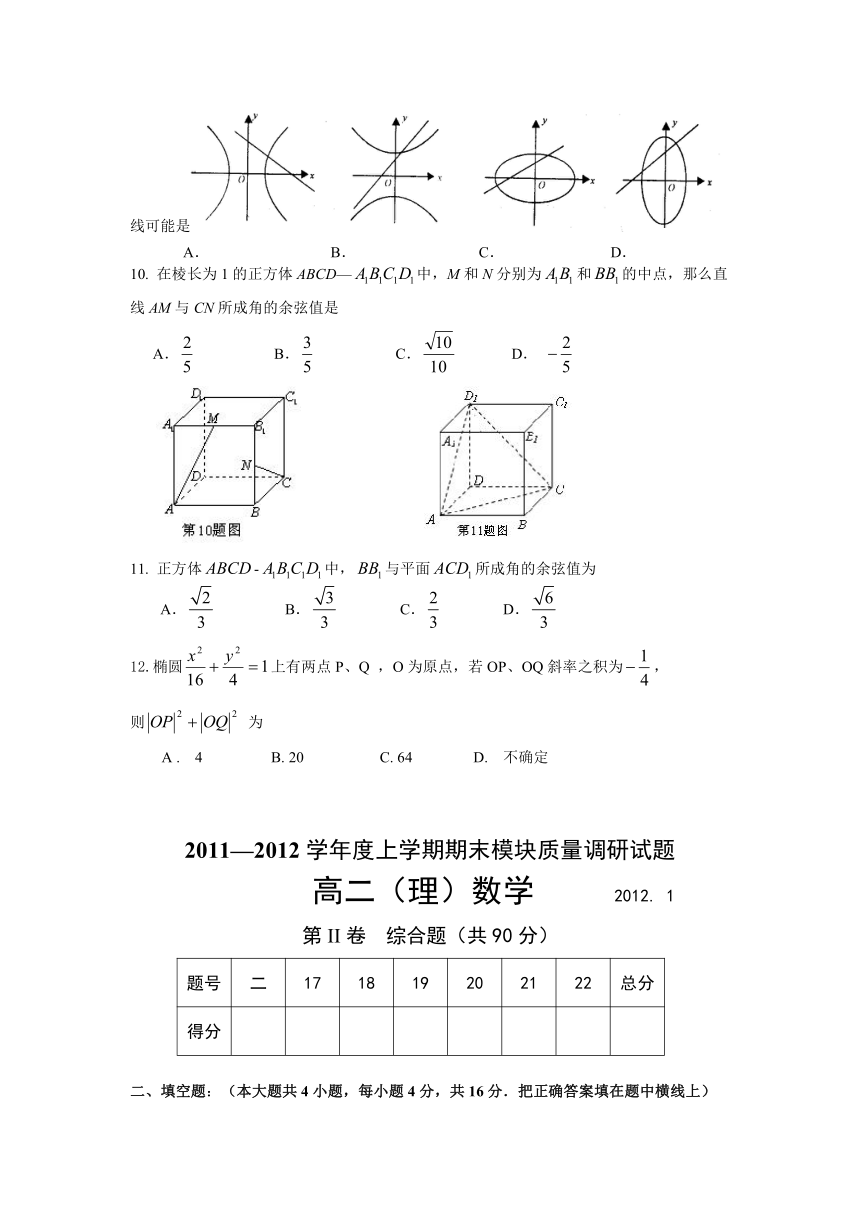
9.已知方程,它们所表示的曲线可能是
A. B. C. D.
10. 在棱长为1的正方体ABCD—中,M和N分别为和的中点,那么直线AM与CN所成角的余弦值是
A. B. C. D.
11. 正方体-中,与平面所成角的余弦值为
A. B. C. D.
12.椭圆上有两点P、Q ,O为原点,若OP、OQ斜率之积为,
则 为
A . 4 B. 20 C. 64 D. 不确定
2011—2012学年度上学期期末模块质量调研试题
高二(理)数学 2012. 1
第II卷 综合题(共90分)
题号
二
17
18
19
20
21
22
总分
得分
二、填空题:(本大题共4小题,每小题4分,共16分.把正确答案填在题中横线上)
13.已知命题,,则:____________.
14.若双曲线的离心率为,则两条渐近线的方程为________________.
15.等差数列的前n项和为Sn,且,.记,如果存在正整数M,使得对一切正整数n,都成立.则M的最小值是 .
16.若不等式组表示的平面区域是一个三角形,则的取值范围是_______.
三、解答题:(本大题共6小题,共74分,解答应写出必要的文字说明,证明过程或演算步骤)
17.(本小题满分12分)
在△ABC中,分别为角A,B,C所对的三边,
(I)求角A;
(II)若,求的值.
18.(本小题满分12分)
设是等差数列,是各项都为正数的等比数列,且,,
。
(I)求,的通项公式;
(II)求数列的前n项和.
19.(本小题满分12分)
某投资商到一开发区投资72万元建起了一座蔬菜加工厂,经营中,第一年支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元.设表示前n年的纯利润总和,(f(n)=前n年的总收入–前n年的总支出–投资额72万元).
(I)该厂从第几年开始盈利?
(II)该厂第几年年平均纯利润达到最大?并求出年平均纯利润的最大值.
20.(本小题满分12分)
已知,,设:函数在上单调递减;q:曲线与x轴交于不同的两点,如果p且q为假命题,p或q为真命题,求实数a的取值范围.
21.(本小题满分12分)
如图所示,矩形ABCD的边AB=,BC=2,PA⊥平面ABCD,PA=2,现有数据:
①;②;③;建立适当的空间直角坐标系,
(I)当BC边上存在点Q,使PQ⊥QD时,可能取所给数据中的哪些值?请说明理由;
(II)在满足(I)的条件下,若取所给数据的最小值时,这样的点Q有几个? 若沿BC方向依次记为,试求二面角的大小.
22.(本小题满分14分)
已知的顶点,在椭圆上,在直线上,且.
(1)当边通过坐标原点时,求的长及的面积;
(2)当,且斜边的长最大时,求所在直线的方程.
2012—2013学年度上学期期末模块质量调研试题
高二(理)数学参考答案 2013.1
一、选择题:(每小题5分,共60分) CCADD BCABA DB
二、填空题:(每小题4分,共16分)
13., 14. 15. 2 16.
三、解答题:
17.解:(1)由
, ……3分 又, ∴。 ……6分
(2),……8分 ∴。……………10分
∵ 。………………………12分
18.解:(1)设的公差为, 的公比为,则依题意有且
由,解得,. ∴,…5分
.………………………………………………6分
(2).…7分,①………8分
,②………………………9分
由②-①得………………10分
===.…12分
19.解:由题意知……4分
(1)由…………7分
由知,从第三年开始盈利.…………………………8分
(2)年平均纯利润…………………10分
当且仅当n=6时等号成立. …………………………11分
年平均纯利润最大值为16万元,
即第6年,投资商年平均纯利润达到最大,年平均纯利润最大值16万元……12分
20.解:由题意知p与q中有且只有一个为真命题,…………………………2分
当0 < a < 1时,函数在(0,+∞)上单调递减;
当,函数在(0,+∞)上不是单调递减;
曲线与x轴交于两点等价于,
即a < 或a > .……………………………………4分
(1)若p正确,q不正确,即函数在(0,+∞)上单调递减,
曲线与x轴不交于两点,
故a∈,即a∈.………………………7分
(2)若p不正确,q正确,即函数在(0,+∞)上不是单调递减,
曲线与x轴交于两点,因此a∈(1,+∞)∩((0,)∪(,+∞)),
即a∈(,+∞).……………………………………………………………10分
综上,a取值范围为[,1)∪(,+∞).…………………………………………12分
21.解:(I)建立如图所示的空间直角坐标系,则各点坐标分别为:
,,,,
设(0≤x≤2), …………………2分
∵∴由PQ⊥QD得
。
∵ ……………4分
∴在所给数据中,可取和两个值. ……6分
(II) 由(Ⅰ)知,此时或,即满足条件的点Q有两个,…8分
根据题意,其坐标为和,……9分
∵PA⊥平面ABCD,∴PA⊥AQ1,PA⊥AQ2,
∴∠Q1AQ2就是二面角Q1-PA-Q2的平面角.……………………10分
由=,
得∠Q1AQ2=30(,∴二面角Q1-PA-Q2的大小为30(.………………………12分
22.解:(1)∵,且边通过点,∴直线的方程为.…1分
设两点坐标分别为.由,得.…3分
∴.………………………4分
又边上的高等于原点到直线的距离.
∴,.………………………6分
(2)设所在直线的方程为,
由得.………………………8分
因为A, B在椭圆上,所以.设两点坐标分别为
,则,,
所以.………………………12分
又因为的长等于点到直线的距离,即.
所以.
所以当时,边最长,(这时)
此时所在直线的方程为.………………………14分
高二(理)数学 2013. 1
注意事项:
1.答题前,请先将自己的姓名、考场、考号在卷首的相应位置填写清楚;
2.选择题答案涂在答题卡上,非选择题用蓝色、黑色钢笔或圆珠笔直接写在试卷上
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的).
1.在中,角所对的边分别是,且,则
A. B. C. D.
2.抛物线焦点坐标是
A.(,0) B.(,0) C. (0, ) D.(0, )
3.“”是“”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.椭圆与双曲线有相同的焦点,则的值是
A. B.1或-2 C.1或 D.1
5.若A,B,当取最小值时,的值为
A.6 B.3 C.2 D.1
6.下列命题中为真命题的是
①“若,则不全为零”的否命题; ②“等腰三角形都相似”的逆命题; ③“若,则不等式的解集为R”的逆否命题。
A.① B.①③ C.②③ D.①②③
7. 设成等比数列,其公比为2,则的值为
A.1 B. C. D.
8.设A是△ABC中的最小角,且,则实数a的取值范围是
A.a≥3 B.a>-1 C.-1<a≤3 D.a>0
9.已知方程,它们所表示的曲线可能是
A. B. C. D.
10. 在棱长为1的正方体ABCD—中,M和N分别为和的中点,那么直线AM与CN所成角的余弦值是
A. B. C. D.
11. 正方体-中,与平面所成角的余弦值为
A. B. C. D.
12.椭圆上有两点P、Q ,O为原点,若OP、OQ斜率之积为,
则 为
A . 4 B. 20 C. 64 D. 不确定
2011—2012学年度上学期期末模块质量调研试题
高二(理)数学 2012. 1
第II卷 综合题(共90分)
题号
二
17
18
19
20
21
22
总分
得分
二、填空题:(本大题共4小题,每小题4分,共16分.把正确答案填在题中横线上)
13.已知命题,,则:____________.
14.若双曲线的离心率为,则两条渐近线的方程为________________.
15.等差数列的前n项和为Sn,且,.记,如果存在正整数M,使得对一切正整数n,都成立.则M的最小值是 .
16.若不等式组表示的平面区域是一个三角形,则的取值范围是_______.
三、解答题:(本大题共6小题,共74分,解答应写出必要的文字说明,证明过程或演算步骤)
17.(本小题满分12分)
在△ABC中,分别为角A,B,C所对的三边,
(I)求角A;
(II)若,求的值.
18.(本小题满分12分)
设是等差数列,是各项都为正数的等比数列,且,,
。
(I)求,的通项公式;
(II)求数列的前n项和.
19.(本小题满分12分)
某投资商到一开发区投资72万元建起了一座蔬菜加工厂,经营中,第一年支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元.设表示前n年的纯利润总和,(f(n)=前n年的总收入–前n年的总支出–投资额72万元).
(I)该厂从第几年开始盈利?
(II)该厂第几年年平均纯利润达到最大?并求出年平均纯利润的最大值.
20.(本小题满分12分)
已知,,设:函数在上单调递减;q:曲线与x轴交于不同的两点,如果p且q为假命题,p或q为真命题,求实数a的取值范围.
21.(本小题满分12分)
如图所示,矩形ABCD的边AB=,BC=2,PA⊥平面ABCD,PA=2,现有数据:
①;②;③;建立适当的空间直角坐标系,
(I)当BC边上存在点Q,使PQ⊥QD时,可能取所给数据中的哪些值?请说明理由;
(II)在满足(I)的条件下,若取所给数据的最小值时,这样的点Q有几个? 若沿BC方向依次记为,试求二面角的大小.
22.(本小题满分14分)
已知的顶点,在椭圆上,在直线上,且.
(1)当边通过坐标原点时,求的长及的面积;
(2)当,且斜边的长最大时,求所在直线的方程.
2012—2013学年度上学期期末模块质量调研试题
高二(理)数学参考答案 2013.1
一、选择题:(每小题5分,共60分) CCADD BCABA DB
二、填空题:(每小题4分,共16分)
13., 14. 15. 2 16.
三、解答题:
17.解:(1)由
, ……3分 又, ∴。 ……6分
(2),……8分 ∴。……………10分
∵ 。………………………12分
18.解:(1)设的公差为, 的公比为,则依题意有且
由,解得,. ∴,…5分
.………………………………………………6分
(2).…7分,①………8分
,②………………………9分
由②-①得………………10分
===.…12分
19.解:由题意知……4分
(1)由…………7分
由知,从第三年开始盈利.…………………………8分
(2)年平均纯利润…………………10分
当且仅当n=6时等号成立. …………………………11分
年平均纯利润最大值为16万元,
即第6年,投资商年平均纯利润达到最大,年平均纯利润最大值16万元……12分
20.解:由题意知p与q中有且只有一个为真命题,…………………………2分
当0 < a < 1时,函数在(0,+∞)上单调递减;
当,函数在(0,+∞)上不是单调递减;
曲线与x轴交于两点等价于,
即a < 或a > .……………………………………4分
(1)若p正确,q不正确,即函数在(0,+∞)上单调递减,
曲线与x轴不交于两点,
故a∈,即a∈.………………………7分
(2)若p不正确,q正确,即函数在(0,+∞)上不是单调递减,
曲线与x轴交于两点,因此a∈(1,+∞)∩((0,)∪(,+∞)),
即a∈(,+∞).……………………………………………………………10分
综上,a取值范围为[,1)∪(,+∞).…………………………………………12分
21.解:(I)建立如图所示的空间直角坐标系,则各点坐标分别为:
,,,,
设(0≤x≤2), …………………2分
∵∴由PQ⊥QD得
。
∵ ……………4分
∴在所给数据中,可取和两个值. ……6分
(II) 由(Ⅰ)知,此时或,即满足条件的点Q有两个,…8分
根据题意,其坐标为和,……9分
∵PA⊥平面ABCD,∴PA⊥AQ1,PA⊥AQ2,
∴∠Q1AQ2就是二面角Q1-PA-Q2的平面角.……………………10分
由=,
得∠Q1AQ2=30(,∴二面角Q1-PA-Q2的大小为30(.………………………12分
22.解:(1)∵,且边通过点,∴直线的方程为.…1分
设两点坐标分别为.由,得.…3分
∴.………………………4分
又边上的高等于原点到直线的距离.
∴,.………………………6分
(2)设所在直线的方程为,
由得.………………………8分
因为A, B在椭圆上,所以.设两点坐标分别为
,则,,
所以.………………………12分
又因为的长等于点到直线的距离,即.
所以.
所以当时,边最长,(这时)
此时所在直线的方程为.………………………14分
同课章节目录
