九年级上册数学第二十六章二次函数单元测试(附答案)
文档属性
| 名称 | 九年级上册数学第二十六章二次函数单元测试(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 246.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-01 15:22:01 | ||
图片预览



文档简介
九年级数学第二十六章二次函数单元测试(附答案)
题号
一、选择题
二、填空题
三、简答题
四、作图题
五、实验,探究题
六、计算题
七、综合题
总分
得分
一、选择题
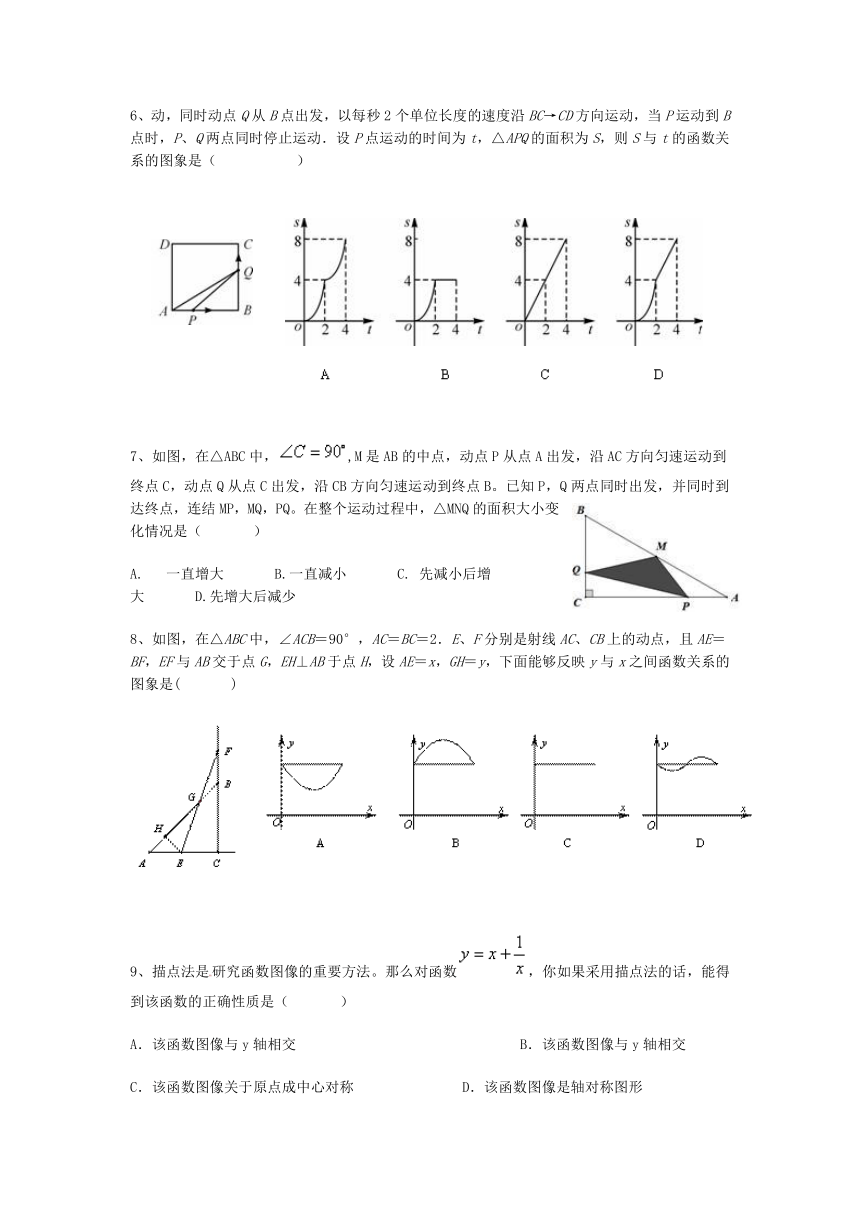
1、如图,等腰Rt()的直角边与正方形的边长均为2,且与在同一直线上,开始时点与点重合,让沿这条直线向右平移,直到点与点重合为止.设的长为,与正方形重合部分(图中阴影部分)的面积为,则与之间的函数关系的图象大致是(?????? )
2、?将二次函数y=—x2的图象向上平移2个单位,再向左平移3个单位,得到新的图象的二次函数表达式是( )
A. ??? ?????B.
C. ????? ?D.
2、?将二次函数y=—x2的图象向上平移2个单位,再向左平移3个单位,得到新的图象的二次函数表达式是( )
A. ??? ?????B.
C. ????? ?D.
3、如图为抛物线的图像,A、B、C 为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是(???? )?????
A.a+b=-1??? ?? B. a-b=-1 ??????C. b<2a ?? D.? ac<0?
???????????????
4、如图是二次函数y=ax2+bx+c(a≠0)的图象所示,若∣ax2+bx+c∣=k(k≠0)有两个不相等的实数根,? 则k的取值范围是(??? )
? A. k<-3 ?????????B. k>-3????????? C. k<3 ???????D. k>3
?
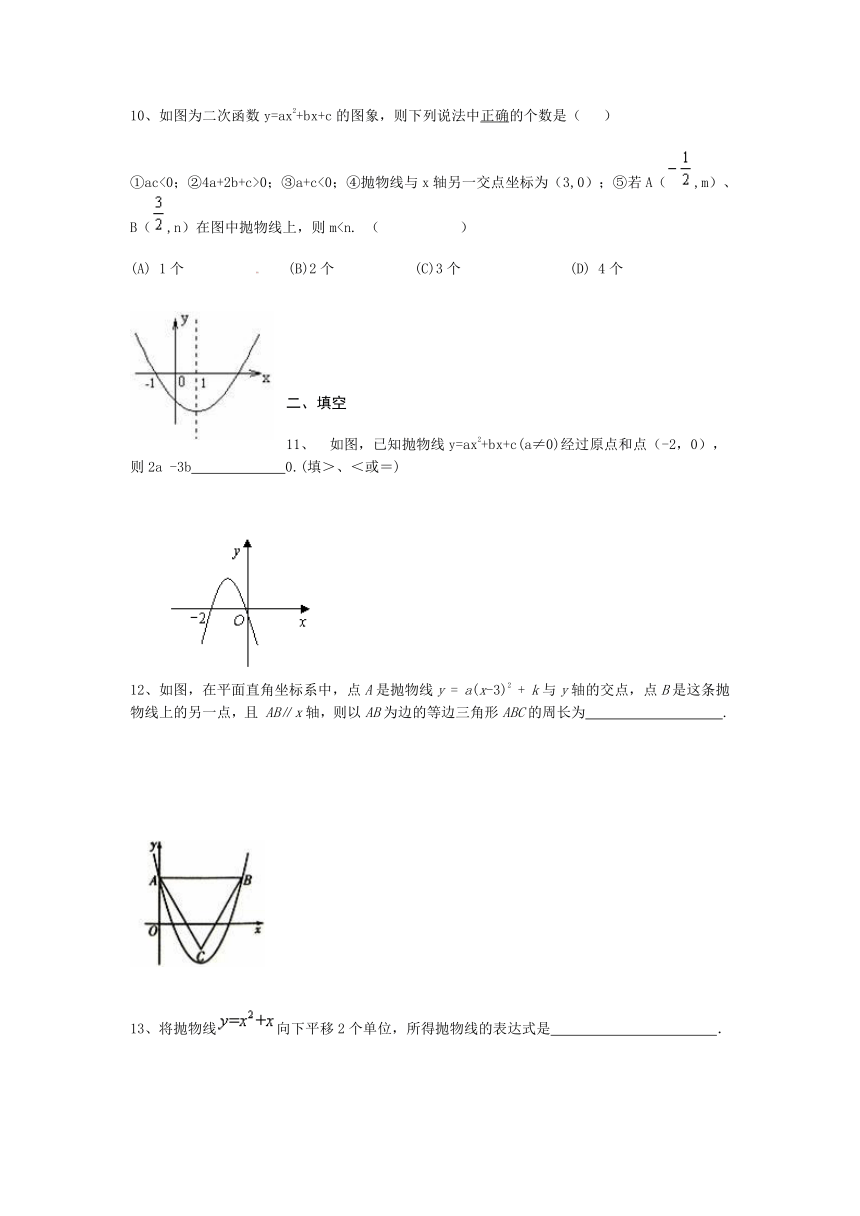
5、如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是(??? ??)
6、动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是(??? ??)
7、如图,在△ABC中,,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B。已知P,Q两点同时出发,并同时到达终点,连结MP,MQ,PQ。在整个运动过程中,△MNQ的面积大小变化情况是(??? )
A.? 一直增大??? B.一直减小??? C. 先减小后增大??? D.先增大后减少
8、如图,在△ABC中,∠ACB=90°,AC=BC=2.E、F分别是射线AC、CB上的动点,且AE=BF,EF与AB交于点G,EH⊥AB于点H,设AE=x,GH=y,下面能够反映y与x之间函数关系的图象是(??? )
9、描点法是研究函数图像的重要方法。那么对函数,你如果采用描点法的话,能得到该函数的正确性质是(??? )
A.该函数图像与y轴相交?????? ?????????B.该函数图像与y轴相交???
C.该函数图像关于原点成中心对称??????? D.该函数图像是轴对称图形
10、如图为二次函数y=ax2+bx+c的图象,则下列说法中正确的个数是(? )
①ac<0;②4a+2b+c>0;③a+c<0;④抛物线与x轴另一交点坐标为(3,0);⑤若A(,m)、B(,n)在图中抛物线上,则m(A) 1个???????(B)2个 ?????(C)3个 ???????(D) 4个
二、填空
11、?如图,已知抛物线y=ax2+bx+c(a≠0)经过原点和点(-2,0),则2a -3b?????? 0.(填>、<或=)
?
12、如图,在平面直角坐标系中,点A是抛物线y = a(x-3)2 + k与y轴的交点,点B是这条抛物线上的另一点,且 AB∥x轴,则以AB为边的等边三角形ABC的周长为????????? .
13、将抛物线向下平移2个单位,所得抛物线的表达式是??????????? .
14、运用图象法解答:如图,已知函数与(a>0,b>0)的图象交于点P,点P的纵坐标为1,则结论:①两函数图象的交点???????? ;②则关于x的方程>0的解为?????????????????????? .
15、已知A、B是抛物线y=x2-4x+3上位置不同的两点,且关于抛物线的对称轴对称,则点A、B的坐标可能是_____________(写出一对即可).
16、已知二次函数(为常数),当取不同的值时,其图象构成一个“抛物线系”.下图分别是当,,,时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是????????????? .
?
17、二次函数的图像与x轴交于B、C两点,点D是线段BC的中点,在x轴上方的A点为抛物线上的动点,连结AD,设AD=m,当∠BAC为锐角时,m的取值范围????????????。
18、已知抛物线与轴交点的横坐标为-1,则a + c=___________.
三、简答题
19、已知反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)
(1)求a的值;
(2)反比例函数的图象是否经过二次函数图象的顶点,请说明理由.
20、如图,将腰长为的等腰Rt△ABC(=90°)放在平面直角坐标系中的第二象限, 使点C的坐标为(,0),点A在y轴上,点B在抛物线上.
(1)写出点A,B的坐标;
(2)求抛物线的解析式;
(3)将三角板ABC绕顶点A逆时针方向旋转90°,到达的位置.请判断点、是否在该抛物线上,并说明理由.
?
四、作图题
21、如图抛物线与x轴相交于点A、B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标.
(2)请你设计一种平移的方法,使平移后抛物线的顶点落要第二象限,
五、实验,探究题
22、请阅读下面材料:
若,?是抛物线(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.有一种方法证明如下:
证明:∵ ,是抛物线(a ≠ 0)上不同的两点, ???????
????? ∴ ????????且 ≠.?
??①-②得 .
?? ∴ .
?∴ .
?又∵ 抛物线(a ≠ 0)的对称轴为,
?∴ 直线为此抛物线的对称轴.
?(1)反之,如果,?是抛物线(a ≠ 0)上不同的
两点,直线 为该抛物线的对称轴,那么自变量取,时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
??(2)利用以上结论解答下面问题:
已知二次函数 当x = 4?时的函数值与x = 2007?时的函数值相等,求x = 2012时的函数值.
六、计算题
23、如下图,已知二次函数图象的顶点坐标为C(1,0),直线与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴上.
(1)求的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为,点P的横坐标为,求与之间的函数关系式,并写出自变量的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
24、杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线的一部分,如图。
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由。
七、综合题
25、已知点A(-1,-1)在抛物线(其中x是自变量)上.
(1)求抛物线的对称轴;
(2)若B点与A点关于抛物线的对称轴对称,问是否存在与抛物线只交于一点B的直线?如果存在,求符合条件的直线解析式;如果不存在,说明理由.
26、如图,在平面直角坐标系中放置一直角三角板,其顶点为,将此三角板绕原点逆时针旋转,得到.
(1)一抛物线经过点、、,求该抛物线的解析式;
(2)设点是在第一象限内抛物线上的一动点,是否存在点,使四边形的面积是面积的倍?若存在,请求出点的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形是哪种形状的四边形?并写出四边形的两条性质.
27、如图,抛物线y=ax2+bx经过点A(4,0),B(2,2). 连结OB,AB.
??? (1)求该抛物线的解析式;
(2)求证:△OAB是等腰直角三角形
(3)将△OAB绕点O按顺时针方向旋转l35°得到△OA′B′,写出△OA′B′ 的边A′B′的中点P的坐标.试判断点P是否在此抛物线上,并说明理由.
28、? 已知:二次函数,其图象对称轴为直线,H经过点().
(1)求此二次函数的解析式.
(2)设该图象与x轴交于B、C两点(B点在C点的左边).请在此二次函数x轴下方的
??? 图象上确定一点E.使△EBC的面积最大.并求出最大面积。
注:二次函数的对称轴是直线.
29、如图,抛物线y=x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断的形状,证明你的结论;
(3)点是x轴上的一个动点,当MC+MD的值最小时,求m的值.
30、如图,设抛物线交x轴于两点,顶点为.以为直径作半圆,圆心为,半圆交y轴负半轴于.
(1)求抛物线的对称轴;
(2)将绕圆心顺时针旋转,得到,如图.求点的坐标;
???????
(3)有一动点在线段上运动,的周长在不断变化时是否存在最小值?若存在,求点的坐标;若不存在,说明理由.
31、如图①②,在平面直角坐标系中,边长为2的等边△CDE恰好与坐标系中的△OAB重合,现将△CDE绕边AB的中点G(G点也是DE的中点),按顺时针方向旋转180°到△C1DE的位置.
(1)求C1点的坐标;
(2)求经过三点O、A、C`的抛物线的解析式;
(3)如图③,⊙G是以AB为直径的圆,过B点作⊙G的切线与x轴相交于点F,求切线BF的解析式;
(4)抛物线上是否存在一点M,使得S△AMF∶S△OAB=16∶3.若存在,请求出点M的坐标;若不存在,请说明理由.
?
32、如图,在平面直角坐标系中,抛物线A(-1,0),B(3,0)C(0,-1)三点。
(1)求该抛物线的表达式;
(2)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形求所有满足条件点P的坐标。
参考答案
一、选择题
1、A
2、C
3、B
4、D
5、D
6、D
7、C
8、C;
9、C
10、C
二、填空题
11、>
12、?18????????
13、.
14、(-3,1) ,x<-3或x>0???????
15、
16、()
17、2<m≤4? ??
18、1 ?????
三、简答题
19、?解:(1)∵反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点(2,2)
∴代入得2=4a+2-1
解得a=.
(2) 反比例函数的图象经过二次函数图象的顶点,理由如下:
∵反比例函数y=的图象过点(2,2)
∴代入得2=,解得k=4.
由(1)可知二次函数的解析式分别为y=x2+x-1
计算可得二次函数y=x2+x-1的顶点坐标为(-2,-2)
∵x=-2时,y==-2.?????????
?∴反比例函数的图象经过二次函数图象的顶点.
20、(1)A(0,2), B(,1);…2’
(2)将B(-3,1)代入函数式得a=,解析式为;…4’
(3)过点作轴于点M,过点B作轴于点N,过点作 轴于点P.……5’??? 在Rt△AB′M与Rt△BAN中,
∵ AB=AB′, ∠AB′M=∠BAN=90°-∠B′AM,∴ Rt△AB′M≌Rt△BAN.……6’
∴ B′M=AN=1,AM=BN=3, ∴ B′(1,).……7’
同理△AC′P≌△CAO,C′P=OA=2,AP=OC=1,可得点C′(2,1);……8’
当x=1时=-1,? 当x=2时=1,
可知点B′、C′在抛物线上.……10’
四、作图题
21、解:(1)把点代入抛物线得,
,
解得.
该二次函数的解析式为.
顶点坐标为.
(2)(答案不唯一,合理即正确)
如先向左平移3个单位,再向上平移4个单位,
得到的二次函数解析式为
,
即.
五、实验,探究题
22、解:(1)结论:自变量取,时函数值相等.
??????????? 证明:∵ ,为抛物线上不同的两点,
?????? ????????由题意得 ????????且≠.
?? ????????①-②,得 .
??????? ????????∵ 直线是抛物线(a ≠ 0)的对称轴,
???????? ???????∴ .
??????? ????????∴ .
???????????? ∴ ,即
(阅卷说明:其他代数证明方法相应给分;直接利用抛物线的对称性而
没有用代数方法进行证明的不给分)
? (2)∵ 二次函数当x = 4?时的函数值与x = 2007?时的函数值相等,
?????? ∴ 由阅读材料可知二次函数的对称轴为直线.
?????? ∴ ,.
?????? ∴ 二次函数的解析式为.
?????? ∵ ,
由(1)知,当x = 2012的函数值与时的函数值相等.
∵ 当x =时的函数值为,
?????? ∴ 当x = 2012 时的函数值为2011.?
六、计算题
23、解:(1) ∵ 点A(3,4)在直线y=x+m上,
∴ 4=3+m.??????????????????????????????
∴ m=1.???????????????????????????????
??????? 设所求二次函数的关系式为y=a(x-1)2.?????
??????? ∵ 点A(3,4)在二次函数y=a(x-1)2的图象上,
??????? ∴ 4=a(3-1)2,
??????? ∴ a=1.???????
∴ 所求二次函数的关系式为y=(x-1)2.
?? 即y=x2-2x+1.??????????????????
(2) 设P、E两点的纵坐标分别为yP和yE .
∴ PE=h=yP-yE??????????????????????
?????? =(x+1)-(x2-2x+1)?
?????? =-x2+3x.?????????????????
?? 即h=-x2+3x (0<x<3).??????????????
(3) 存在.?????????????????????????
解法1:要使四边形DCEP是平行四边形,必需有PE=DC.
∵ 点D在直线y=x+1上,
∴ 点D的坐标为(1,2),
∴ -x2+3x=2 .
即x2-3x+2=0 .???????????????????????
解之,得? x1=2,x2=1 (不合题意,舍去)???
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形. ?
解法2:要使四边形DCEP是平行四边形,必需有BP∥CE.?
设直线CE的函数关系式为y=x+b.
∵ 直线CE 经过点C(1,0),
∴ 0=1+b,
∴ b=-1 .
∴ 直线CE的函数关系式为y=x-1 .
∴ ???得x2-3x+2=0.??????
解之,得? x1=2,x2=1 (不合题意,舍去)??
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形.
24、解:(1)=
∵,∴函数的最大值是。
答:演员弹跳的最大高度是米。
(2)当x=4时,=3.4=BC,所以这次表演成功。
七、综合题
25、解:(1)已知点A(-1,-1)在已知抛物线上
则,??????????
即
解得 ,????????????????? …………分
当时,函数为一次函数,不合题意,舍去
当时,抛物线的解析式为???????? …………4分
由抛物线的解析式知其对称轴为??????? …………5分
(2)∵点B与点A关于对称,且A(-1,-1),
∴B()?????????????????????????? …………6分
当直线过B()且与y轴平行时,此直线与抛物线只有一个交点,
此时的直线为?????????????????? …………8分
当直线过B()且不与y轴平行时,
设直线与抛物线只交于一点B
则,?????????????????????? …………10分
即 ①
把代入,得,…………11分
即???????????? …………12分
由⊿=0,得? ②
由①,②得????????????????????????????????
故所求的直线为????????????? …………14分
26、解:(1)是由绕原点逆时针旋转得到的,
又,.----------1分
设抛物线的解析式为,
抛物线经过点、、,
,解之得,
满足条件的抛物线的解析式为.----------3分
(2)为第一象限内抛物线上的一动点,
设,则,点坐标满足.
连结,
.----------5分
假设四边形的面积是面积的倍,则
,
即,解之得,此时,即.----------7分
存在点,使四边形的面积是面积的倍. ----------8分
(3)四边形为等腰梯形,答案不唯一,下面性质中的任意2个均可.
①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等;③等腰梯形上底与下底平行;④等腰梯形两腰相等. ----------10分
或用符号表示:
①或;②;③;④.----------10分
27、
?
?
28、
BC=4
29、(1)把点A(-1,0)的坐标代入抛物线的解析式y=x2+bx-2,
?????? 整理后解得,
所以抛物线的解析式为?
?顶点.??????????
(2).,,.
是直角三角形.
(3)作出点关于轴的对称点,则,.连接交轴于点,
根据轴对称性及两点之间线段最短可知,的值最小.
设抛物线的对称轴交轴于点..
...
30、解:(1)对称轴为直线x=1??? 2’
(2)? A (-1,0) , B (3,0) ,M(1,0)
所以圆M的半径为2????? ?????1’
???????? 1’
???
(3)?? 顶点坐标为D(1,-1)???
??????? D(1,-1)关于x轴的对称点D‘(1,1)?? 1’
??????? 则直线CD‘为???????? 1’
??????? 则CD‘与X轴的交点即为所求的Q点为???? 2’
31、?(1)C`(3,)
? (2)∵抛物线过原点O(0,0),设抛物线解析式为y=ax2+bx
把A(2,0),C`(3,)带入,得?? 解得a=,b=-
∴抛物线解析式为y=x2-x
(3)∵∠ABF=90°,∠BAF=60°,∴∠AFB=30°
又AB=2??? ∴AF=4??? ∴OF=2?????? ∴F(-2,0)
???? 设直线BF的解析式为y=kx+b
把B(1,),F(-2,0)带入,得??? 解得k=,b=
∴直线BF的解析式为y=x+
?? (4)①当M在x轴上方时,存在M(x,x2-x)
S△AMF:S△OAB=[×4×(x2-x)]:[×2×4]=16:3
得x2-2x-8=0,解得x1=4,x2=-2
当x1=4时,y=×42-×4=;
当x1=-2时,y=×(-2)2-×(-2)=
∴M1(4,),M2(-2,)
②当M在x轴下方时,不存在,设点M(x,x2-x)
? S△AMF:S△OAB=[-×4×(x2-x)]:[×2×4]=16:3
得x2-2x+8=0,b2-4ac<0 无解
?? 综上所述,存在点的坐标为M1(4,),M2(-2,)
?
32、解:(1)设该抛物线的表达式为y=ax2+bx+c根据题意,得
?????????? ?????解之,得
???? ∴所求抛物线的表达式为y=x2-x-1
????? (2)①AB为边时,只要PQ∥AB且PQ=AB=4即可。
???????? 又知点Q在y轴上,∴点P的横坐标为4或-4,这时符合条件的点P有两个,分别记为P1,P2 .
而当x=4时,y=;当x=-4时,y=7,
此时P1(4,)P2(-4,7)
②当AB为对角线时,只要线段PQ与线段AB互相平分即可
又知点Q在Y轴上,且线段AB中点的横坐标为1
∴点P的横坐标为2,这时符合条件的P只有一个记为P3
而且当x=2时y=-1 ,此时P3(2,-1)
综上,满足条件的P为P1(4,)P2(-4,7)P3(2,-1)
题号
一、选择题
二、填空题
三、简答题
四、作图题
五、实验,探究题
六、计算题
七、综合题
总分
得分
一、选择题
1、如图,等腰Rt()的直角边与正方形的边长均为2,且与在同一直线上,开始时点与点重合,让沿这条直线向右平移,直到点与点重合为止.设的长为,与正方形重合部分(图中阴影部分)的面积为,则与之间的函数关系的图象大致是(?????? )
2、?将二次函数y=—x2的图象向上平移2个单位,再向左平移3个单位,得到新的图象的二次函数表达式是( )
A. ??? ?????B.
C. ????? ?D.
2、?将二次函数y=—x2的图象向上平移2个单位,再向左平移3个单位,得到新的图象的二次函数表达式是( )
A. ??? ?????B.
C. ????? ?D.
3、如图为抛物线的图像,A、B、C 为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是(???? )?????
A.a+b=-1??? ?? B. a-b=-1 ??????C. b<2a ?? D.? ac<0?
???????????????
4、如图是二次函数y=ax2+bx+c(a≠0)的图象所示,若∣ax2+bx+c∣=k(k≠0)有两个不相等的实数根,? 则k的取值范围是(??? )
? A. k<-3 ?????????B. k>-3????????? C. k<3 ???????D. k>3
?
5、如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是(??? ??)
6、动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是(??? ??)
7、如图,在△ABC中,,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B。已知P,Q两点同时出发,并同时到达终点,连结MP,MQ,PQ。在整个运动过程中,△MNQ的面积大小变化情况是(??? )
A.? 一直增大??? B.一直减小??? C. 先减小后增大??? D.先增大后减少
8、如图,在△ABC中,∠ACB=90°,AC=BC=2.E、F分别是射线AC、CB上的动点,且AE=BF,EF与AB交于点G,EH⊥AB于点H,设AE=x,GH=y,下面能够反映y与x之间函数关系的图象是(??? )
9、描点法是研究函数图像的重要方法。那么对函数,你如果采用描点法的话,能得到该函数的正确性质是(??? )
A.该函数图像与y轴相交?????? ?????????B.该函数图像与y轴相交???
C.该函数图像关于原点成中心对称??????? D.该函数图像是轴对称图形
10、如图为二次函数y=ax2+bx+c的图象,则下列说法中正确的个数是(? )
①ac<0;②4a+2b+c>0;③a+c<0;④抛物线与x轴另一交点坐标为(3,0);⑤若A(,m)、B(,n)在图中抛物线上,则m
二、填空
11、?如图,已知抛物线y=ax2+bx+c(a≠0)经过原点和点(-2,0),则2a -3b?????? 0.(填>、<或=)
?
12、如图,在平面直角坐标系中,点A是抛物线y = a(x-3)2 + k与y轴的交点,点B是这条抛物线上的另一点,且 AB∥x轴,则以AB为边的等边三角形ABC的周长为????????? .
13、将抛物线向下平移2个单位,所得抛物线的表达式是??????????? .
14、运用图象法解答:如图,已知函数与(a>0,b>0)的图象交于点P,点P的纵坐标为1,则结论:①两函数图象的交点???????? ;②则关于x的方程>0的解为?????????????????????? .
15、已知A、B是抛物线y=x2-4x+3上位置不同的两点,且关于抛物线的对称轴对称,则点A、B的坐标可能是_____________(写出一对即可).
16、已知二次函数(为常数),当取不同的值时,其图象构成一个“抛物线系”.下图分别是当,,,时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是????????????? .
?
17、二次函数的图像与x轴交于B、C两点,点D是线段BC的中点,在x轴上方的A点为抛物线上的动点,连结AD,设AD=m,当∠BAC为锐角时,m的取值范围????????????。
18、已知抛物线与轴交点的横坐标为-1,则a + c=___________.
三、简答题
19、已知反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)
(1)求a的值;
(2)反比例函数的图象是否经过二次函数图象的顶点,请说明理由.
20、如图,将腰长为的等腰Rt△ABC(=90°)放在平面直角坐标系中的第二象限, 使点C的坐标为(,0),点A在y轴上,点B在抛物线上.
(1)写出点A,B的坐标;
(2)求抛物线的解析式;
(3)将三角板ABC绕顶点A逆时针方向旋转90°,到达的位置.请判断点、是否在该抛物线上,并说明理由.
?
四、作图题
21、如图抛物线与x轴相交于点A、B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标.
(2)请你设计一种平移的方法,使平移后抛物线的顶点落要第二象限,
五、实验,探究题
22、请阅读下面材料:
若,?是抛物线(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.有一种方法证明如下:
证明:∵ ,是抛物线(a ≠ 0)上不同的两点, ???????
????? ∴ ????????且 ≠.?
??①-②得 .
?? ∴ .
?∴ .
?又∵ 抛物线(a ≠ 0)的对称轴为,
?∴ 直线为此抛物线的对称轴.
?(1)反之,如果,?是抛物线(a ≠ 0)上不同的
两点,直线 为该抛物线的对称轴,那么自变量取,时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
??(2)利用以上结论解答下面问题:
已知二次函数 当x = 4?时的函数值与x = 2007?时的函数值相等,求x = 2012时的函数值.
六、计算题
23、如下图,已知二次函数图象的顶点坐标为C(1,0),直线与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴上.
(1)求的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为,点P的横坐标为,求与之间的函数关系式,并写出自变量的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
24、杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线的一部分,如图。
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由。
七、综合题
25、已知点A(-1,-1)在抛物线(其中x是自变量)上.
(1)求抛物线的对称轴;
(2)若B点与A点关于抛物线的对称轴对称,问是否存在与抛物线只交于一点B的直线?如果存在,求符合条件的直线解析式;如果不存在,说明理由.
26、如图,在平面直角坐标系中放置一直角三角板,其顶点为,将此三角板绕原点逆时针旋转,得到.
(1)一抛物线经过点、、,求该抛物线的解析式;
(2)设点是在第一象限内抛物线上的一动点,是否存在点,使四边形的面积是面积的倍?若存在,请求出点的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形是哪种形状的四边形?并写出四边形的两条性质.
27、如图,抛物线y=ax2+bx经过点A(4,0),B(2,2). 连结OB,AB.
??? (1)求该抛物线的解析式;
(2)求证:△OAB是等腰直角三角形
(3)将△OAB绕点O按顺时针方向旋转l35°得到△OA′B′,写出△OA′B′ 的边A′B′的中点P的坐标.试判断点P是否在此抛物线上,并说明理由.
28、? 已知:二次函数,其图象对称轴为直线,H经过点().
(1)求此二次函数的解析式.
(2)设该图象与x轴交于B、C两点(B点在C点的左边).请在此二次函数x轴下方的
??? 图象上确定一点E.使△EBC的面积最大.并求出最大面积。
注:二次函数的对称轴是直线.
29、如图,抛物线y=x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断的形状,证明你的结论;
(3)点是x轴上的一个动点,当MC+MD的值最小时,求m的值.
30、如图,设抛物线交x轴于两点,顶点为.以为直径作半圆,圆心为,半圆交y轴负半轴于.
(1)求抛物线的对称轴;
(2)将绕圆心顺时针旋转,得到,如图.求点的坐标;
???????
(3)有一动点在线段上运动,的周长在不断变化时是否存在最小值?若存在,求点的坐标;若不存在,说明理由.
31、如图①②,在平面直角坐标系中,边长为2的等边△CDE恰好与坐标系中的△OAB重合,现将△CDE绕边AB的中点G(G点也是DE的中点),按顺时针方向旋转180°到△C1DE的位置.
(1)求C1点的坐标;
(2)求经过三点O、A、C`的抛物线的解析式;
(3)如图③,⊙G是以AB为直径的圆,过B点作⊙G的切线与x轴相交于点F,求切线BF的解析式;
(4)抛物线上是否存在一点M,使得S△AMF∶S△OAB=16∶3.若存在,请求出点M的坐标;若不存在,请说明理由.
?
32、如图,在平面直角坐标系中,抛物线A(-1,0),B(3,0)C(0,-1)三点。
(1)求该抛物线的表达式;
(2)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形求所有满足条件点P的坐标。
参考答案
一、选择题
1、A
2、C
3、B
4、D
5、D
6、D
7、C
8、C;
9、C
10、C
二、填空题
11、>
12、?18????????
13、.
14、(-3,1) ,x<-3或x>0???????
15、
16、()
17、2<m≤4? ??
18、1 ?????
三、简答题
19、?解:(1)∵反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点(2,2)
∴代入得2=4a+2-1
解得a=.
(2) 反比例函数的图象经过二次函数图象的顶点,理由如下:
∵反比例函数y=的图象过点(2,2)
∴代入得2=,解得k=4.
由(1)可知二次函数的解析式分别为y=x2+x-1
计算可得二次函数y=x2+x-1的顶点坐标为(-2,-2)
∵x=-2时,y==-2.?????????
?∴反比例函数的图象经过二次函数图象的顶点.
20、(1)A(0,2), B(,1);…2’
(2)将B(-3,1)代入函数式得a=,解析式为;…4’
(3)过点作轴于点M,过点B作轴于点N,过点作 轴于点P.……5’??? 在Rt△AB′M与Rt△BAN中,
∵ AB=AB′, ∠AB′M=∠BAN=90°-∠B′AM,∴ Rt△AB′M≌Rt△BAN.……6’
∴ B′M=AN=1,AM=BN=3, ∴ B′(1,).……7’
同理△AC′P≌△CAO,C′P=OA=2,AP=OC=1,可得点C′(2,1);……8’
当x=1时=-1,? 当x=2时=1,
可知点B′、C′在抛物线上.……10’
四、作图题
21、解:(1)把点代入抛物线得,
,
解得.
该二次函数的解析式为.
顶点坐标为.
(2)(答案不唯一,合理即正确)
如先向左平移3个单位,再向上平移4个单位,
得到的二次函数解析式为
,
即.
五、实验,探究题
22、解:(1)结论:自变量取,时函数值相等.
??????????? 证明:∵ ,为抛物线上不同的两点,
?????? ????????由题意得 ????????且≠.
?? ????????①-②,得 .
??????? ????????∵ 直线是抛物线(a ≠ 0)的对称轴,
???????? ???????∴ .
??????? ????????∴ .
???????????? ∴ ,即
(阅卷说明:其他代数证明方法相应给分;直接利用抛物线的对称性而
没有用代数方法进行证明的不给分)
? (2)∵ 二次函数当x = 4?时的函数值与x = 2007?时的函数值相等,
?????? ∴ 由阅读材料可知二次函数的对称轴为直线.
?????? ∴ ,.
?????? ∴ 二次函数的解析式为.
?????? ∵ ,
由(1)知,当x = 2012的函数值与时的函数值相等.
∵ 当x =时的函数值为,
?????? ∴ 当x = 2012 时的函数值为2011.?
六、计算题
23、解:(1) ∵ 点A(3,4)在直线y=x+m上,
∴ 4=3+m.??????????????????????????????
∴ m=1.???????????????????????????????
??????? 设所求二次函数的关系式为y=a(x-1)2.?????
??????? ∵ 点A(3,4)在二次函数y=a(x-1)2的图象上,
??????? ∴ 4=a(3-1)2,
??????? ∴ a=1.???????
∴ 所求二次函数的关系式为y=(x-1)2.
?? 即y=x2-2x+1.??????????????????
(2) 设P、E两点的纵坐标分别为yP和yE .
∴ PE=h=yP-yE??????????????????????
?????? =(x+1)-(x2-2x+1)?
?????? =-x2+3x.?????????????????
?? 即h=-x2+3x (0<x<3).??????????????
(3) 存在.?????????????????????????
解法1:要使四边形DCEP是平行四边形,必需有PE=DC.
∵ 点D在直线y=x+1上,
∴ 点D的坐标为(1,2),
∴ -x2+3x=2 .
即x2-3x+2=0 .???????????????????????
解之,得? x1=2,x2=1 (不合题意,舍去)???
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形. ?
解法2:要使四边形DCEP是平行四边形,必需有BP∥CE.?
设直线CE的函数关系式为y=x+b.
∵ 直线CE 经过点C(1,0),
∴ 0=1+b,
∴ b=-1 .
∴ 直线CE的函数关系式为y=x-1 .
∴ ???得x2-3x+2=0.??????
解之,得? x1=2,x2=1 (不合题意,舍去)??
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形.
24、解:(1)=
∵,∴函数的最大值是。
答:演员弹跳的最大高度是米。
(2)当x=4时,=3.4=BC,所以这次表演成功。
七、综合题
25、解:(1)已知点A(-1,-1)在已知抛物线上
则,??????????
即
解得 ,????????????????? …………分
当时,函数为一次函数,不合题意,舍去
当时,抛物线的解析式为???????? …………4分
由抛物线的解析式知其对称轴为??????? …………5分
(2)∵点B与点A关于对称,且A(-1,-1),
∴B()?????????????????????????? …………6分
当直线过B()且与y轴平行时,此直线与抛物线只有一个交点,
此时的直线为?????????????????? …………8分
当直线过B()且不与y轴平行时,
设直线与抛物线只交于一点B
则,?????????????????????? …………10分
即 ①
把代入,得,…………11分
即???????????? …………12分
由⊿=0,得? ②
由①,②得????????????????????????????????
故所求的直线为????????????? …………14分
26、解:(1)是由绕原点逆时针旋转得到的,
又,.----------1分
设抛物线的解析式为,
抛物线经过点、、,
,解之得,
满足条件的抛物线的解析式为.----------3分
(2)为第一象限内抛物线上的一动点,
设,则,点坐标满足.
连结,
.----------5分
假设四边形的面积是面积的倍,则
,
即,解之得,此时,即.----------7分
存在点,使四边形的面积是面积的倍. ----------8分
(3)四边形为等腰梯形,答案不唯一,下面性质中的任意2个均可.
①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等;③等腰梯形上底与下底平行;④等腰梯形两腰相等. ----------10分
或用符号表示:
①或;②;③;④.----------10分
27、
?
?
28、
BC=4
29、(1)把点A(-1,0)的坐标代入抛物线的解析式y=x2+bx-2,
?????? 整理后解得,
所以抛物线的解析式为?
?顶点.??????????
(2).,,.
是直角三角形.
(3)作出点关于轴的对称点,则,.连接交轴于点,
根据轴对称性及两点之间线段最短可知,的值最小.
设抛物线的对称轴交轴于点..
...
30、解:(1)对称轴为直线x=1??? 2’
(2)? A (-1,0) , B (3,0) ,M(1,0)
所以圆M的半径为2????? ?????1’
???????? 1’
???
(3)?? 顶点坐标为D(1,-1)???
??????? D(1,-1)关于x轴的对称点D‘(1,1)?? 1’
??????? 则直线CD‘为???????? 1’
??????? 则CD‘与X轴的交点即为所求的Q点为???? 2’
31、?(1)C`(3,)
? (2)∵抛物线过原点O(0,0),设抛物线解析式为y=ax2+bx
把A(2,0),C`(3,)带入,得?? 解得a=,b=-
∴抛物线解析式为y=x2-x
(3)∵∠ABF=90°,∠BAF=60°,∴∠AFB=30°
又AB=2??? ∴AF=4??? ∴OF=2?????? ∴F(-2,0)
???? 设直线BF的解析式为y=kx+b
把B(1,),F(-2,0)带入,得??? 解得k=,b=
∴直线BF的解析式为y=x+
?? (4)①当M在x轴上方时,存在M(x,x2-x)
S△AMF:S△OAB=[×4×(x2-x)]:[×2×4]=16:3
得x2-2x-8=0,解得x1=4,x2=-2
当x1=4时,y=×42-×4=;
当x1=-2时,y=×(-2)2-×(-2)=
∴M1(4,),M2(-2,)
②当M在x轴下方时,不存在,设点M(x,x2-x)
? S△AMF:S△OAB=[-×4×(x2-x)]:[×2×4]=16:3
得x2-2x+8=0,b2-4ac<0 无解
?? 综上所述,存在点的坐标为M1(4,),M2(-2,)
?
32、解:(1)设该抛物线的表达式为y=ax2+bx+c根据题意,得
?????????? ?????解之,得
???? ∴所求抛物线的表达式为y=x2-x-1
????? (2)①AB为边时,只要PQ∥AB且PQ=AB=4即可。
???????? 又知点Q在y轴上,∴点P的横坐标为4或-4,这时符合条件的点P有两个,分别记为P1,P2 .
而当x=4时,y=;当x=-4时,y=7,
此时P1(4,)P2(-4,7)
②当AB为对角线时,只要线段PQ与线段AB互相平分即可
又知点Q在Y轴上,且线段AB中点的横坐标为1
∴点P的横坐标为2,这时符合条件的P只有一个记为P3
而且当x=2时y=-1 ,此时P3(2,-1)
综上,满足条件的P为P1(4,)P2(-4,7)P3(2,-1)
