1.1.2.3循环结构课件(下)
文档属性
| 名称 | 1.1.2.3循环结构课件(下) |  | |
| 格式 | zip | ||
| 文件大小 | 75.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-01 18:11:27 | ||
图片预览




文档简介
课件19张PPT。程序框图的循环结构(下) 湖南省耒阳市振兴学校
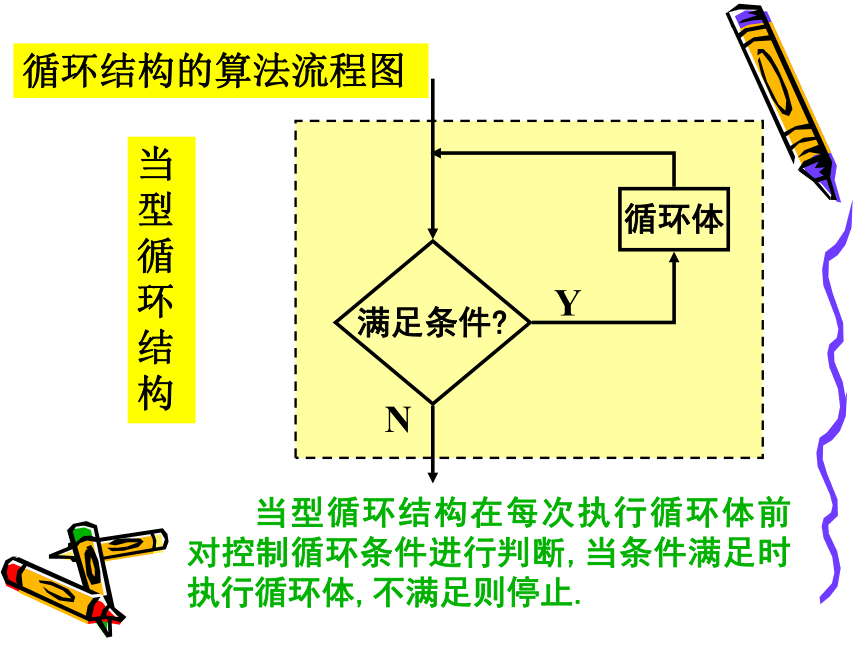
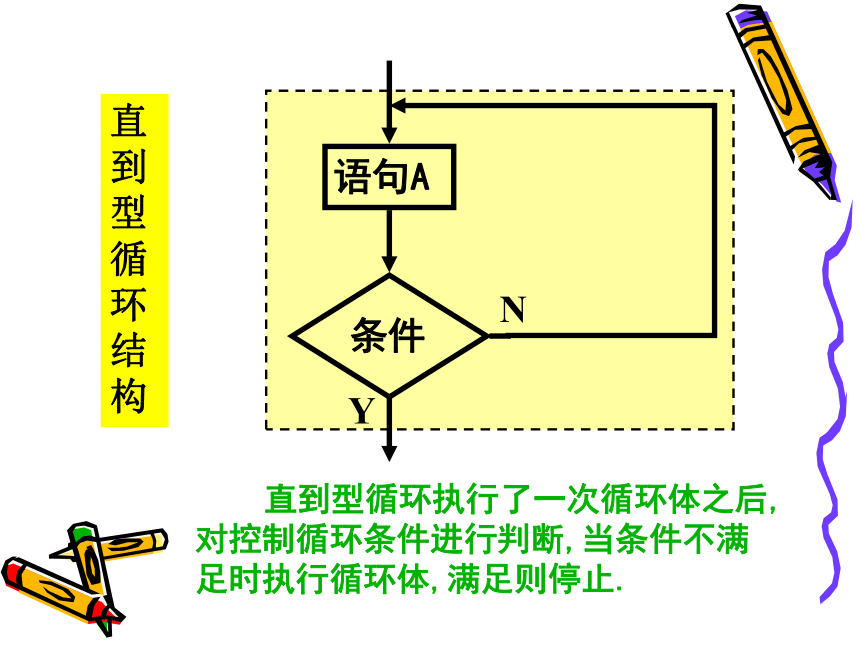
高中数学老师欧阳文丰制作1.循环结构分为两种——当型和直到型. 当型循环在每次执行循环体前对循环条件进行判断,当条件满足时执行循环体,不满足则停止;(当条件满足时反复执行循环体) 直到型循环在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,满足则停止.(反复执行循环体,直到条件满足) 复习巩固当型循环结构满足条件?循环体YN 当型循环结构在每次执行循环体前对控制循环条件进行判断,当条件满足时执行循环体,不满足则停止.循环结构的算法流程图直到型循环结构条件语句AYN 直到型循环执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,满足则停止.2.循环结构的设计步骤(1)确定循环结构的循环变量和初始条件;
(2)确定算法中需要反复执行的部分,即循环体;
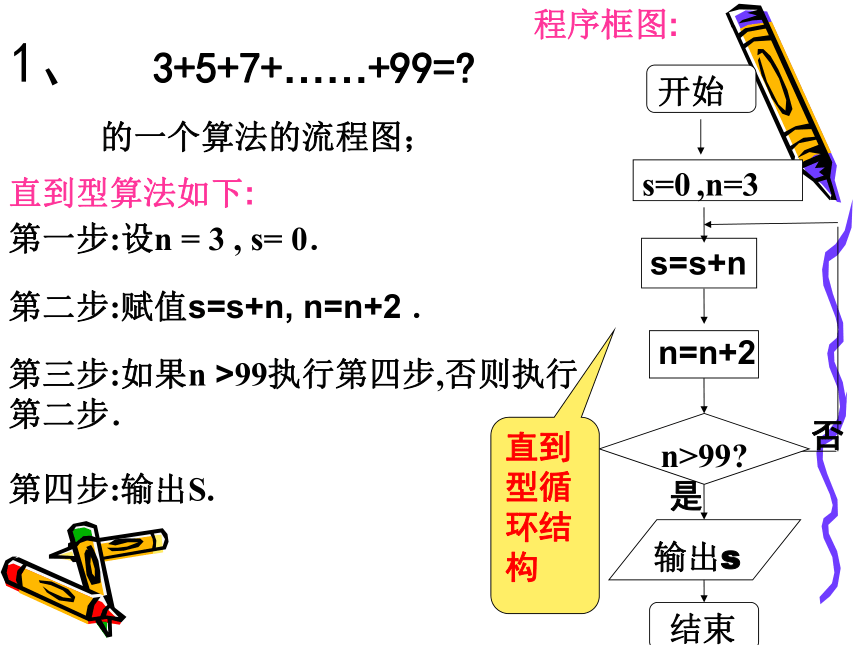
(3)确定循环的终止条件.3.循环结构的三要素循环变量,循环体、循环的终止条件.例1、 3+5+7+……+99=?分析:只需要一个累加变量S和计数变量n.将累加变量S初值赋为0,计数变量n从3到99变化,n初值赋为首项3, 步长为公差2.
设n = 3 , s=0.s=s+n,n=n+2. 典型例题讲解n>99?开始s=0 ,n=3 输出s 结束s=s+n n=n+2否是1、 3+5+7+……+99=?直到型循环结构的一个算法的流程图;第二步:赋值s=s+n, n=n+2 .第三步:如果n >99执行第四步,否则执行
第二步.第四步:输出S.第一步:设n = 3 , s= 0.直到型算法如下:程序框图:开始n=1,S=0S≤2008?是S=S+nn=n+1否输出n-1结束当型循环结构2、画出求n的最小正整数值,使
1+2+3+4+…+n>2008的一个算法的流程图;当型算法如下:第一步:设n = 1 , s= 0.第三步:赋值s=s+n, n=n+1 .第二步:如果s ≤2008执行第三步,
否则执行第四步.第四步:输出n-1.程序框图:设i= 0 , s = 0 .i=i+1,s=s+通项. i既可作
计数变量, 又可作求和的项数变量.等差(比)数列求和的设计要素的一个算法的流程图; 随堂练习 例3 某工厂2005年的年生产总值为200万元,技术革新后预计以后每年的年生产总值都比上一年增长5%.设计一个程序框图,输出预计年生产总值超过300万元的最早年份.第三步,判断所得的结果是否大于300. 若是,则输出该年的年份; 否则,返回第二步.第一步, 输入2005年的年生产总值.第二步,计算下一年的年生产总值.算法分析:(3)控制条件:当“a>300”时终止循环.(1)循环体:设a为某年的年生产总值,t为年生产总值的年增长量,n为年份,则t=0.05a,a=a+t,n=n+1.(2)初始值:n=2005,a=200.循环结构:例3.某工厂2004年的生产总值为200万元,技术革新后预计以后每年的生产总值比上一年增加5%,问最早需要哪一年年生产总值超过300万元.写出计算的一个算法,并画出相应的程序框图.第一步:n = 0 , a = 200 , r = 0.05.第二步:T = ar(计算年增量).第三步:a = a + T(计算年产值).第四步:如果a ≤ 300,那么n = n + 1,重复执行第二步. 第五步:否则, N = 2004 + n.第六步:输出N.例3、某工厂2005年生产总值200万元,技术革新后预计以后每年的年生产总值比上一年增长5%,设计一个程序框图,输出预计年生产总值超过300万元的最早年份。是否直到型循环结构程序框图是否a≤300?当型循环结构程序框图等差(比)数列求通项的设计要素(1)等差数列, 设i=1, a= 首项.i=i+1 , a=a+公差.(2)等比数列, 设i=1, a= 首项 .i=i+1 , r=q-1,
T=ar,a=a+T.例4:画出用二分法求方程x2 – 2 = 0的近似根(精确度为0.005)的程序框图.第一步:令f (x) = x2 – 2,给定精确度d.第四步:若f(a)?f(m) > 0,则令a = m;否则,令b = m.第五步:判断| a – b | < ε或f (m) = 0是否成立.若是,则m为方程的近似根;若否,则返回第三步. 第二步:确定区间[a , b],满足f (a)?f(b) < 0.第三步:取区间中点m = (a + b)/2.程序框图布置作业:P20练习
P21习题1.1A组第2题
高中数学老师欧阳文丰制作1.循环结构分为两种——当型和直到型. 当型循环在每次执行循环体前对循环条件进行判断,当条件满足时执行循环体,不满足则停止;(当条件满足时反复执行循环体) 直到型循环在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,满足则停止.(反复执行循环体,直到条件满足) 复习巩固当型循环结构满足条件?循环体YN 当型循环结构在每次执行循环体前对控制循环条件进行判断,当条件满足时执行循环体,不满足则停止.循环结构的算法流程图直到型循环结构条件语句AYN 直到型循环执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,满足则停止.2.循环结构的设计步骤(1)确定循环结构的循环变量和初始条件;
(2)确定算法中需要反复执行的部分,即循环体;
(3)确定循环的终止条件.3.循环结构的三要素循环变量,循环体、循环的终止条件.例1、 3+5+7+……+99=?分析:只需要一个累加变量S和计数变量n.将累加变量S初值赋为0,计数变量n从3到99变化,n初值赋为首项3, 步长为公差2.
设n = 3 , s=0.s=s+n,n=n+2. 典型例题讲解n>99?开始s=0 ,n=3 输出s 结束s=s+n n=n+2否是1、 3+5+7+……+99=?直到型循环结构的一个算法的流程图;第二步:赋值s=s+n, n=n+2 .第三步:如果n >99执行第四步,否则执行
第二步.第四步:输出S.第一步:设n = 3 , s= 0.直到型算法如下:程序框图:开始n=1,S=0S≤2008?是S=S+nn=n+1否输出n-1结束当型循环结构2、画出求n的最小正整数值,使
1+2+3+4+…+n>2008的一个算法的流程图;当型算法如下:第一步:设n = 1 , s= 0.第三步:赋值s=s+n, n=n+1 .第二步:如果s ≤2008执行第三步,
否则执行第四步.第四步:输出n-1.程序框图:设i= 0 , s = 0 .i=i+1,s=s+通项. i既可作
计数变量, 又可作求和的项数变量.等差(比)数列求和的设计要素的一个算法的流程图; 随堂练习 例3 某工厂2005年的年生产总值为200万元,技术革新后预计以后每年的年生产总值都比上一年增长5%.设计一个程序框图,输出预计年生产总值超过300万元的最早年份.第三步,判断所得的结果是否大于300. 若是,则输出该年的年份; 否则,返回第二步.第一步, 输入2005年的年生产总值.第二步,计算下一年的年生产总值.算法分析:(3)控制条件:当“a>300”时终止循环.(1)循环体:设a为某年的年生产总值,t为年生产总值的年增长量,n为年份,则t=0.05a,a=a+t,n=n+1.(2)初始值:n=2005,a=200.循环结构:例3.某工厂2004年的生产总值为200万元,技术革新后预计以后每年的生产总值比上一年增加5%,问最早需要哪一年年生产总值超过300万元.写出计算的一个算法,并画出相应的程序框图.第一步:n = 0 , a = 200 , r = 0.05.第二步:T = ar(计算年增量).第三步:a = a + T(计算年产值).第四步:如果a ≤ 300,那么n = n + 1,重复执行第二步. 第五步:否则, N = 2004 + n.第六步:输出N.例3、某工厂2005年生产总值200万元,技术革新后预计以后每年的年生产总值比上一年增长5%,设计一个程序框图,输出预计年生产总值超过300万元的最早年份。是否直到型循环结构程序框图是否a≤300?当型循环结构程序框图等差(比)数列求通项的设计要素(1)等差数列, 设i=1, a= 首项.i=i+1 , a=a+公差.(2)等比数列, 设i=1, a= 首项 .i=i+1 , r=q-1,
T=ar,a=a+T.例4:画出用二分法求方程x2 – 2 = 0的近似根(精确度为0.005)的程序框图.第一步:令f (x) = x2 – 2,给定精确度d.第四步:若f(a)?f(m) > 0,则令a = m;否则,令b = m.第五步:判断| a – b | < ε或f (m) = 0是否成立.若是,则m为方程的近似根;若否,则返回第三步. 第二步:确定区间[a , b],满足f (a)?f(b) < 0.第三步:取区间中点m = (a + b)/2.程序框图布置作业:P20练习
P21习题1.1A组第2题
