北师大版数学九年级下册 第三章 几何圆与相似 综合训练(含解析)
文档属性
| 名称 | 北师大版数学九年级下册 第三章 几何圆与相似 综合训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 09:43:21 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学几何圆与相似
一.相交弦定理
1.如图,⊙O的弦AB、CD相交于点P,若AP=6,BP=8,CP=4,则CD长为( )
A.16 B.24 C.12 D.不能确定
2.如图,已知⊙O中,弦AB、CD交于P,AP=PB=4,CP=2,则CD= .
3.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP= .
4.如图,已知圆O,弦AB、CD相交于点M.
(1)求证:AM MB=CM MD;
(2)若M为CD中点,且圆O的半径为3,OM=2,求AM MB的值.
二.切割线定理
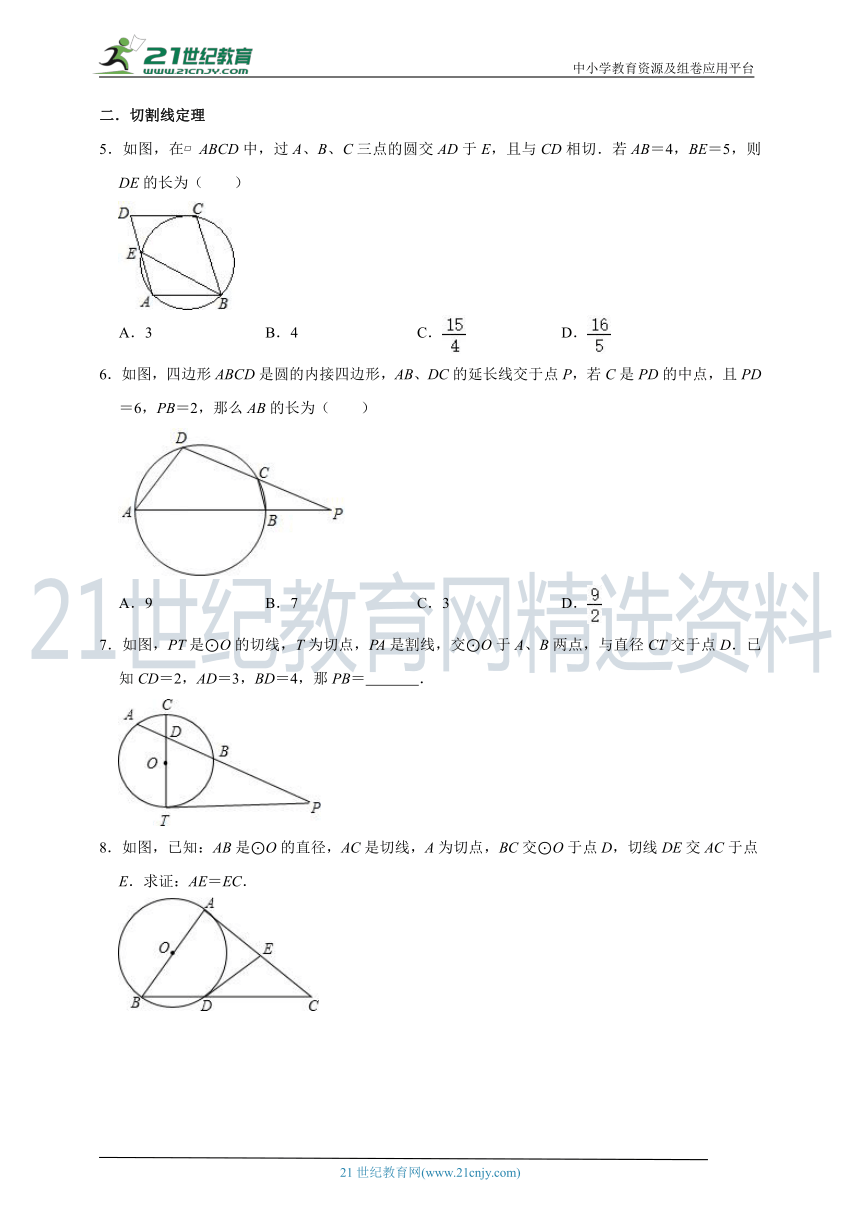
5.如图,在 ABCD中,过A、B、C三点的圆交AD于E,且与CD相切.若AB=4,BE=5,则DE的长为( )
A.3 B.4 C. D.
6.如图,四边形ABCD是圆的内接四边形,AB、DC的延长线交于点P,若C是PD的中点,且PD=6,PB=2,那么AB的长为( )
A.9 B.7 C.3 D.
7.如图,PT是⊙O的切线,T为切点,PA是割线,交⊙O于A、B两点,与直径CT交于点D.已知CD=2,AD=3,BD=4,那PB= .
8.如图,已知:AB是⊙O的直径,AC是切线,A为切点,BC交⊙O于点D,切线DE交AC于点E.求证:AE=EC.
三.圆幂定理
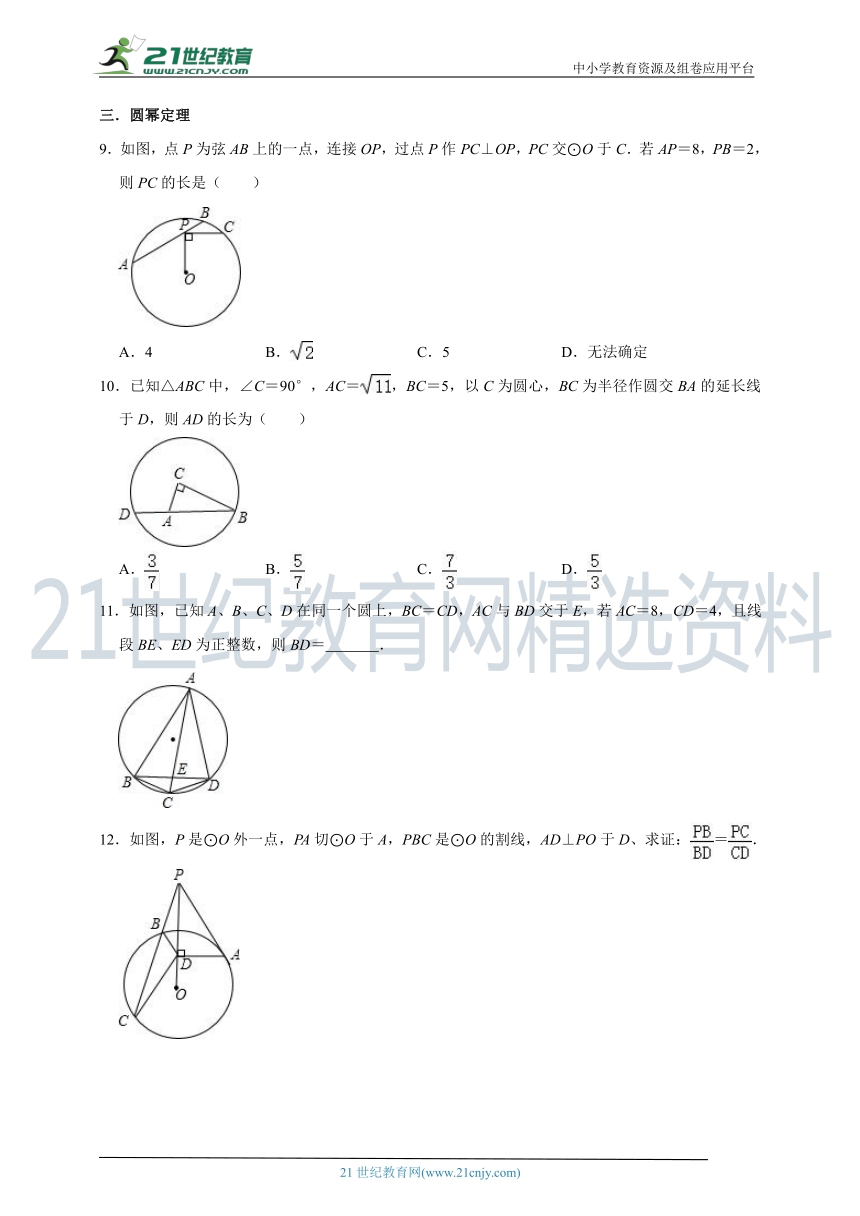
9.如图,点P为弦AB上的一点,连接OP,过点P作PC⊥OP,PC交⊙O于C.若AP=8,PB=2,则PC的长是( )
A.4 B. C.5 D.无法确定
10.已知△ABC中,∠C=90°,AC=,BC=5,以C为圆心,BC为半径作圆交BA的延长线于D,则AD的长为( )
A. B. C. D.
11.如图,已知A、B、C、D在同一个圆上,BC=CD,AC与BD交于E,若AC=8,CD=4,且线段BE、ED为正整数,则BD= .
12.如图,P是⊙O外一点,PA切⊙O于A,PBC是⊙O的割线,AD⊥PO于D、求证:=.
参考答案与试题解析
一.试题(共12小题)
1.如图,⊙O的弦AB、CD相交于点P,若AP=6,BP=8,CP=4,则CD长为( )
A.16 B.24 C.12 D.不能确定
【解答】解:∵AP BP=CP DP,
∴PD=,
∵AP=6,BP=8,CP=4,
∴PD=12,
∴CD=PC+PD=12+4=16.
故选:A.
2.如图,已知⊙O中,弦AB、CD交于P,AP=PB=4,CP=2,则CD= 10 .
【解答】解:∵弦AB、CD交于P,
∴PA PB=PC PD,
∴4×4=2×PD,
解得,PD=8,
∴CD=PC+PD=10,
故答案为:10.
3.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP= 6 .
【解答】解:由相交弦定理得,AP BP=CP DP,
则DP==6,
故答案为:6.
4.如图,已知圆O,弦AB、CD相交于点M.
(1)求证:AM MB=CM MD;
(2)若M为CD中点,且圆O的半径为3,OM=2,求AM MB的值.
【解答】解:(1)∵∠A=∠C,∠D=∠B,
∴△ADM∽△CBM
∴,
即AM MB=CM MD.
(2)连接OM、OC.
∵M为CD中点,
∴OM⊥CD
在Rt△OMC中,
∵OC=3,OM=2
∴CM=DM=,
由(1)知AM MB=CM MD.
∴AM MB= =5.
5.如图,在 ABCD中,过A、B、C三点的圆交AD于E,且与CD相切.若AB=4,BE=5,则DE的长为( )
A.3 B.4 C. D.
【解答】解:连接CE;
∵,
∴∠BAE=∠EBC+∠BEC;
∵∠DCB=∠DCE+∠BCE,
由弦切角定理知:∠DCE=∠EBC,
由平行四边形的性质知:∠DCB=∠BAE,
∴∠BEC=∠BCE,即BC=BE=5,
∴AD=5;
由切割线定理知:DE=DC2÷DA=,
故选:D.
6.如图,四边形ABCD是圆的内接四边形,AB、DC的延长线交于点P,若C是PD的中点,且PD=6,PB=2,那么AB的长为( )
A.9 B.7 C.3 D.
【解答】解:∵C是PD的中点,PD=6,
∴PC=CD=PD=3,
由切割线定理得,PC PD=PB PA,即3×6=2×PB,
解得,PB=9,
∴AB=PA﹣PB=7,
故选:B.
7.如图,PT是⊙O的切线,T为切点,PA是割线,交⊙O于A、B两点,与直径CT交于点D.已知CD=2,AD=3,BD=4,那PB= 20 .
【解答】解:∵AD BD=CD DT,
∴TD=,
∵CD=2,AD=3,BD=4,
∴TD=6,
∵PT是⊙O的切线,PA是割线,
∴PT2=PA PB,
∵CT为直径,
∴PT2=PD2﹣TD2,
∴PA PB=PD2﹣TD2,
即(PB+7)PB=(PB+4)2﹣62,
解得PB=20.
故答案为:20.
8.如图,已知:AB是⊙O的直径,AC是切线,A为切点,BC交⊙O于点D,切线DE交AC于点E.求证:AE=EC.
【解答】解:如图,连接AD,
∵AB是圆的直径.
∴∠ADB=90°,则∠ADC=90°
∴∠DAC+∠C=90°
∵AE,DE是圆的切线.
∴AE=DE
∴∠DAE=∠ADE
又∵∠DAE+∠C=∠ADE+∠EDC=90°
∴∠EDC=∠C
∴DE=EC
∴AE=EC
9.如图,点P为弦AB上的一点,连接OP,过点P作PC⊥OP,PC交⊙O于C.若AP=8,PB=2,则PC的长是( )
A.4 B. C.5 D.无法确定
【解答】解:延长CP交圆于一点D,
∵PC⊥OP,
∴PC=PD(垂径定理),
∴PC2=PA PB,
∵AP=8,PB=2,
∴PC2=2×8,
解得PC=4.
故选:A.
10.已知△ABC中,∠C=90°,AC=,BC=5,以C为圆心,BC为半径作圆交BA的延长线于D,则AD的长为( )
A. B. C. D.
【解答】解:延长AC与圆相交于E、F,
则AF=5﹣,
AE=5+,
又AB===6,由相交弦定理AD AB=AE AF得
AD=,
=,
=.
故选:C.
11.如图,已知A、B、C、D在同一个圆上,BC=CD,AC与BD交于E,若AC=8,CD=4,且线段BE、ED为正整数,则BD= 7 .
【解答】解:∵BC=CD,
∴∠BAC=∠DAC,
∵∠DBC=∠DAC,
∴∠BAC=∠DBC,
又∵∠BCE=∠ACB,
∴△ABC∽△BEC,
∴BC2=CE AC,
∵AC=8,CD=4,
∴EC=2,AE=6,
由相交弦定理得,BE DE=AE EC,
即BE DE=12,
又线段BE、ED为正整数,
且在△BCD中,BC+CD>BE+DE,
所以可得BE=3、DE=4或BE=4、DE=3,
所以BD=BE+DE=7.
故答案为:7.
12.如图,P是⊙O外一点,PA切⊙O于A,PBC是⊙O的割线,AD⊥PO于D、求证:=.
【解答】解:连接OA,OC,
∵PA是切线,
∴∠PAO=∠PDA=90°,
又∵∠APD=∠OPA,
∴△APD∽OPA,
∴=,
∴PA2=PD PO,
又∵PA是切线,
∴PA2=PB PC
∴PA2=PD PO=PB PC
又∵∠CPD=∠OPB,
∴△PCD∽△POB
∴
又△POC∽△PBD,则
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
初中数学几何圆与相似
一.相交弦定理
1.如图,⊙O的弦AB、CD相交于点P,若AP=6,BP=8,CP=4,则CD长为( )
A.16 B.24 C.12 D.不能确定
2.如图,已知⊙O中,弦AB、CD交于P,AP=PB=4,CP=2,则CD= .
3.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP= .
4.如图,已知圆O,弦AB、CD相交于点M.
(1)求证:AM MB=CM MD;
(2)若M为CD中点,且圆O的半径为3,OM=2,求AM MB的值.
二.切割线定理
5.如图,在 ABCD中,过A、B、C三点的圆交AD于E,且与CD相切.若AB=4,BE=5,则DE的长为( )
A.3 B.4 C. D.
6.如图,四边形ABCD是圆的内接四边形,AB、DC的延长线交于点P,若C是PD的中点,且PD=6,PB=2,那么AB的长为( )
A.9 B.7 C.3 D.
7.如图,PT是⊙O的切线,T为切点,PA是割线,交⊙O于A、B两点,与直径CT交于点D.已知CD=2,AD=3,BD=4,那PB= .
8.如图,已知:AB是⊙O的直径,AC是切线,A为切点,BC交⊙O于点D,切线DE交AC于点E.求证:AE=EC.
三.圆幂定理
9.如图,点P为弦AB上的一点,连接OP,过点P作PC⊥OP,PC交⊙O于C.若AP=8,PB=2,则PC的长是( )
A.4 B. C.5 D.无法确定
10.已知△ABC中,∠C=90°,AC=,BC=5,以C为圆心,BC为半径作圆交BA的延长线于D,则AD的长为( )
A. B. C. D.
11.如图,已知A、B、C、D在同一个圆上,BC=CD,AC与BD交于E,若AC=8,CD=4,且线段BE、ED为正整数,则BD= .
12.如图,P是⊙O外一点,PA切⊙O于A,PBC是⊙O的割线,AD⊥PO于D、求证:=.
参考答案与试题解析
一.试题(共12小题)
1.如图,⊙O的弦AB、CD相交于点P,若AP=6,BP=8,CP=4,则CD长为( )
A.16 B.24 C.12 D.不能确定
【解答】解:∵AP BP=CP DP,
∴PD=,
∵AP=6,BP=8,CP=4,
∴PD=12,
∴CD=PC+PD=12+4=16.
故选:A.
2.如图,已知⊙O中,弦AB、CD交于P,AP=PB=4,CP=2,则CD= 10 .
【解答】解:∵弦AB、CD交于P,
∴PA PB=PC PD,
∴4×4=2×PD,
解得,PD=8,
∴CD=PC+PD=10,
故答案为:10.
3.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP= 6 .
【解答】解:由相交弦定理得,AP BP=CP DP,
则DP==6,
故答案为:6.
4.如图,已知圆O,弦AB、CD相交于点M.
(1)求证:AM MB=CM MD;
(2)若M为CD中点,且圆O的半径为3,OM=2,求AM MB的值.
【解答】解:(1)∵∠A=∠C,∠D=∠B,
∴△ADM∽△CBM
∴,
即AM MB=CM MD.
(2)连接OM、OC.
∵M为CD中点,
∴OM⊥CD
在Rt△OMC中,
∵OC=3,OM=2
∴CM=DM=,
由(1)知AM MB=CM MD.
∴AM MB= =5.
5.如图,在 ABCD中,过A、B、C三点的圆交AD于E,且与CD相切.若AB=4,BE=5,则DE的长为( )
A.3 B.4 C. D.
【解答】解:连接CE;
∵,
∴∠BAE=∠EBC+∠BEC;
∵∠DCB=∠DCE+∠BCE,
由弦切角定理知:∠DCE=∠EBC,
由平行四边形的性质知:∠DCB=∠BAE,
∴∠BEC=∠BCE,即BC=BE=5,
∴AD=5;
由切割线定理知:DE=DC2÷DA=,
故选:D.
6.如图,四边形ABCD是圆的内接四边形,AB、DC的延长线交于点P,若C是PD的中点,且PD=6,PB=2,那么AB的长为( )
A.9 B.7 C.3 D.
【解答】解:∵C是PD的中点,PD=6,
∴PC=CD=PD=3,
由切割线定理得,PC PD=PB PA,即3×6=2×PB,
解得,PB=9,
∴AB=PA﹣PB=7,
故选:B.
7.如图,PT是⊙O的切线,T为切点,PA是割线,交⊙O于A、B两点,与直径CT交于点D.已知CD=2,AD=3,BD=4,那PB= 20 .
【解答】解:∵AD BD=CD DT,
∴TD=,
∵CD=2,AD=3,BD=4,
∴TD=6,
∵PT是⊙O的切线,PA是割线,
∴PT2=PA PB,
∵CT为直径,
∴PT2=PD2﹣TD2,
∴PA PB=PD2﹣TD2,
即(PB+7)PB=(PB+4)2﹣62,
解得PB=20.
故答案为:20.
8.如图,已知:AB是⊙O的直径,AC是切线,A为切点,BC交⊙O于点D,切线DE交AC于点E.求证:AE=EC.
【解答】解:如图,连接AD,
∵AB是圆的直径.
∴∠ADB=90°,则∠ADC=90°
∴∠DAC+∠C=90°
∵AE,DE是圆的切线.
∴AE=DE
∴∠DAE=∠ADE
又∵∠DAE+∠C=∠ADE+∠EDC=90°
∴∠EDC=∠C
∴DE=EC
∴AE=EC
9.如图,点P为弦AB上的一点,连接OP,过点P作PC⊥OP,PC交⊙O于C.若AP=8,PB=2,则PC的长是( )
A.4 B. C.5 D.无法确定
【解答】解:延长CP交圆于一点D,
∵PC⊥OP,
∴PC=PD(垂径定理),
∴PC2=PA PB,
∵AP=8,PB=2,
∴PC2=2×8,
解得PC=4.
故选:A.
10.已知△ABC中,∠C=90°,AC=,BC=5,以C为圆心,BC为半径作圆交BA的延长线于D,则AD的长为( )
A. B. C. D.
【解答】解:延长AC与圆相交于E、F,
则AF=5﹣,
AE=5+,
又AB===6,由相交弦定理AD AB=AE AF得
AD=,
=,
=.
故选:C.
11.如图,已知A、B、C、D在同一个圆上,BC=CD,AC与BD交于E,若AC=8,CD=4,且线段BE、ED为正整数,则BD= 7 .
【解答】解:∵BC=CD,
∴∠BAC=∠DAC,
∵∠DBC=∠DAC,
∴∠BAC=∠DBC,
又∵∠BCE=∠ACB,
∴△ABC∽△BEC,
∴BC2=CE AC,
∵AC=8,CD=4,
∴EC=2,AE=6,
由相交弦定理得,BE DE=AE EC,
即BE DE=12,
又线段BE、ED为正整数,
且在△BCD中,BC+CD>BE+DE,
所以可得BE=3、DE=4或BE=4、DE=3,
所以BD=BE+DE=7.
故答案为:7.
12.如图,P是⊙O外一点,PA切⊙O于A,PBC是⊙O的割线,AD⊥PO于D、求证:=.
【解答】解:连接OA,OC,
∵PA是切线,
∴∠PAO=∠PDA=90°,
又∵∠APD=∠OPA,
∴△APD∽OPA,
∴=,
∴PA2=PD PO,
又∵PA是切线,
∴PA2=PB PC
∴PA2=PD PO=PB PC
又∵∠CPD=∠OPB,
∴△PCD∽△POB
∴
又△POC∽△PBD,则
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
