初中物理压强综合题练习 (含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
初中物理压强综合题练习
一.压强的大小及其计算(共4小题)
1.如图,实心圆柱体甲、乙的密度均为3×103kg/m3,甲的质量为6kg,底面积为200cm2,乙的质量为12kg,底面积为300cm2。水平地面上的轻质薄壁容器丙内盛有9cm深的水,容器上部分高度为下部分高度的五分之一,容器下底面积为1000cm2。若把甲沿水平方向切割Δh的高度,切割下来的部分竖直缓慢浸没在丙容器的水中,液面的上升高度Δh水与切割的高度Δh的部分关系如图丁所示。求:
(1)圆柱体甲的体积V甲;
(2)容器丙中水的重力;
(3)若将圆柱体乙放入原装有9cm深水的容器丙中,此时容器丙对水平地面的压强。
2.A、B两物体均为质量分布均匀的实心正方体,A物体放在水平地面上,将B物体叠放在A物体上,如图甲所示。若沿竖直方向将B物体切去一部分,A对地面的压强与切去部分的宽度的关系如图乙所示,已知A、B物体的边长分别为20cm、10cm。求:
(1)A物体的密度;
(2)B物体的重力;
(3)现将A、B两物体分别置于水平地面上,如图丙所示。在正方体A、B上沿竖直方向按相同比例k截下一部分,并将截下的部分分别叠放在对方剩余部分上,若叠放后A、B剩余部分对水平地面的压强相等,则k的值为多少?
3.如图所示,底面积不同足够高的圆柱形容器甲、乙(S甲>S乙)置于水平地面上。
①若容器甲重为9.8牛,底面积为1×10﹣2米2,内部盛有深度为0.4米的水。求:
(a)水对容器甲底部的压强p水;
(b)容器甲对水平地面的压强p地。
②若容器甲、乙中的液体A、B对容器底部的压强相等。为使A液体对容器甲底部的压强大于B液体对容器乙底部的压强,有如下方案:(a)在容器甲、乙中同时抽取相同质量的液体;(b)在容器甲、乙中同时加入相同高度的原有液体。请分析每种方案的可行性。
4.如图所示,密度为2×103千克/米3、边长为0.1米均匀正方体甲和底面积为2×10﹣2米2的薄壁柱形容器乙放在水平地面上,乙容器足够高,内盛有0.1米深的水。
(1)求正方体甲的质量m甲。
(2)求水对乙容器底部的压强p乙。
(3)在甲的上部水平截去体积为V后,甲对水平地面的压强变为p甲′;将截取部分放入乙容器中,水对乙容器底部的压强变为p乙′,且p甲′=p乙′。试求水平截去体积V的大小。
二.液体的压强的计算(共6小题)
5.为了维护桃源沅水大桥,使用吊车向河底投放圆柱形混凝土构件如图甲所示,在整个投放过程中,混凝土构件以0.05m/s的速度匀速竖直下降。图乙是钢丝绳的拉力F随时间t变化的图像。当t=0s时吊车开始投放,混凝土构件到100s时结束,此时构件竖立在河中。(已知混凝土的密度为2.6×103kg/m3,钢铁的密度为7.8×103kg/m3,g取10N/kg,水的阻力可以忽略不计)求:
(1)混凝土构件的体积;
(2)投放结束时混凝土构件顶部受到水的压强;
(3)通过计算说明这种混凝土构件混凝土与钢筋的质量之比。
6.育才中学携手重庆机床集团打造了劳动教育社会实践基地,小明同学在基地加工了一个工件如图甲所示,由上下两个不同物质组成圆柱体连接在一起,上半部分A高10cm,底面积50cm2,其质量为400g,下半部分B为高10cm的正方体,B物质的密度为2g/cm3,另有一底面积200cm2,高13.5cm,重2N的圆柱形容器放在水平地面上,如图乙所示,内装2000cm3的水。小明想进一步研究激光切割技术,于是沿水平方向对工件进行切割,并将切割部分竖直放入水中冷却(不计水的汽化损失),则:
(1)未将工件放入水中时,水对容器底的压强是多少Pa?
(2)总共水平切去多少cm时,切割部分恰好在水中悬浮?
(3)某次切割后,工件剩会部分对地面压强能否和放入切制部分的容器对地面的压强相等?若能,请求出切去部分的高度;若不能,请通过计算说明理由。
7.如图所示,不吸水的长方体A固定在体积不计的轻杆下端,位于水平地面上的圆柱形容器内,杆上端固定不动。容器内盛有10cm深的水,物体下表面刚好与容器内的水面相平。往容器中缓慢注水,加水过程中水没有溢出。当加500cm3的水时,轻杆受力为6N,容器底部受到的压强较注水前变化了Δp1;当加2000cm3的水时,轻杆受力为3N,容器底部受到的压强较注水前变化了Δp2,且Δp1:Δp2=1:4.(ρ水=1.0×103kg/m3)求:
(1)加水前水对容器底的压强;
(2)加2000cm3的水时,加入水的质量;
(3)物块A的重力GA。
8.如图所示,装有水的薄壁轻质圆柱形容器甲与圆柱形物块乙等高,放置于水平地面上,甲中水的深度为0.1米,底面积为0.02米2,求:
(1)水对容器底部的压强p水。
(2)容器内水的质量m水。
(3)若水的深度是容器高度的,甲的底面积是乙的2倍,乙的密度是水的3倍,现将乙
放入容器甲中,求:水对容器底的压强与容器对地面的压强的比值。
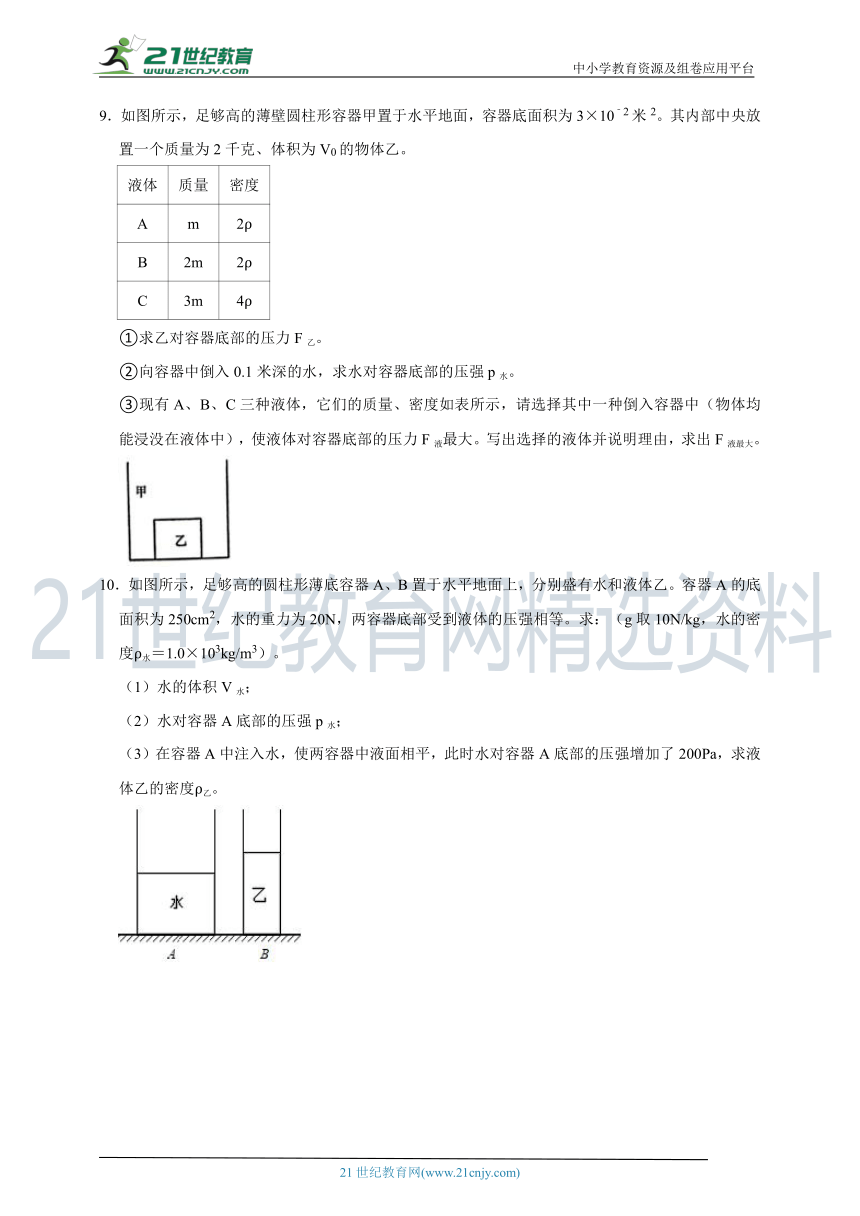
9.如图所示,足够高的薄壁圆柱形容器甲置于水平地面,容器底面积为3×10﹣2米2。其内部中央放置一个质量为2千克、体积为V0的物体乙。
液体 质量 密度
A m 2ρ
B 2m 2ρ
C 3m 4ρ
①求乙对容器底部的压力F乙。
②向容器中倒入0.1米深的水,求水对容器底部的压强p水。
③现有A、B、C三种液体,它们的质量、密度如表所示,请选择其中一种倒入容器中(物体均能浸没在液体中),使液体对容器底部的压力F液最大。写出选择的液体并说明理由,求出F液最大。
10.如图所示,足够高的圆柱形薄底容器A、B置于水平地面上,分别盛有水和液体乙。容器A的底面积为250cm2,水的重力为20N,两容器底部受到液体的压强相等。求:(g取10N/kg,水的密度ρ水=1.0×103kg/m3)。
(1)水的体积V水;
(2)水对容器A底部的压强p水;
(3)在容器A中注入水,使两容器中液面相平,此时水对容器A底部的压强增加了200Pa,求液体乙的密度ρ乙。
参考答案与试题解析
一.压强的大小及其计算(共4小题)
1.如图,实心圆柱体甲、乙的密度均为3×103kg/m3,甲的质量为6kg,底面积为200cm2,乙的质量为12kg,底面积为300cm2。水平地面上的轻质薄壁容器丙内盛有9cm深的水,容器上部分高度为下部分高度的五分之一,容器下底面积为1000cm2。若把甲沿水平方向切割Δh的高度,切割下来的部分竖直缓慢浸没在丙容器的水中,液面的上升高度Δh水与切割的高度Δh的部分关系如图丁所示。求:
(1)圆柱体甲的体积V甲;
(2)容器丙中水的重力;
(3)若将圆柱体乙放入原装有9cm深水的容器丙中,此时容器丙对水平地面的压强。
【解答】解:(1)根据题意,由密度公式ρ=可得甲的体积为V甲=;
(2)容器中水的质量为m水=ρ水V水=1.0g/cm3×9cm×1000cm2=9000g=9kg;
由重力计算公式G=mg可得容器中水的重力为G水=m水g=9kg×10N/kg=90N;
(3)根据题意,由丁图可知,Δh=5cm时,Δh水=lcm,然后Δh水上升更快,表明其底面积减小了,所以容器下部分的高度为h下=9cm+lcm=10cm,则上部分的高度为h上==×10cm=2cm;
根据丁图可知,当Δh=5cm,Δh水=lcm时刚好是上下部分的分界线,而水上升的体积等于甲浸没在水中的体积,则有Δh'水S丙上=Δh'S甲;
则容器丙上部分的底面积为S丙上=;
将乙放入丙内时,下部分装有水的体积为V下=(S丙下﹣S乙)h下=( 1000cm2﹣300cm2)×10cm=7000cm3;
所以剩余的水的体积为V余=V水﹣V下=1000cm2×9cm﹣7000cm3=2000cm3;
而将乙放入丙内时,上部分能装的水的体积为V上=(S丙上﹣S乙)h上=(500cm2﹣300cm2)×2cm=400cm3;
由于V余>V上,所以上部分的水的体积为V上=400cm3,其余溢出了,
故容器丙中剩余水的总质量为m′水=(7000cm3+400cm3)×1.0g/cm3=7400g=7.4kg
所以将乙放入丙内时,对水平面的压力等于总重力,即F=G总=(7.4kg+12kg)×10N/kg=194N;
根据压强的公式p=可得:对水平面的压强为p=;
答:(1)圆柱体甲的体积为2×10﹣3m3;
(2)容器丙中水的重力为90N;
(3)容器丙对水平地面的压强为1940Pa。
2.A、B两物体均为质量分布均匀的实心正方体,A物体放在水平地面上,将B物体叠放在A物体上,如图甲所示。若沿竖直方向将B物体切去一部分,A对地面的压强与切去部分的宽度的关系如图乙所示,已知A、B物体的边长分别为20cm、10cm。求:
(1)A物体的密度;
(2)B物体的重力;
(3)现将A、B两物体分别置于水平地面上,如图丙所示。在正方体A、B上沿竖直方向按相同比例k截下一部分,并将截下的部分分别叠放在对方剩余部分上,若叠放后A、B剩余部分对水平地面的压强相等,则k的值为多少?
【解答】解:(1)A的边长LA=20cm=0.2m,
B的边长LB=10cm=0.1m,
A的底面积SA=LA2=(0.2m)2=0.04m2,
B的底面积SB=LB2=(0.1m)2=0.01m2,
A对地面的压强与切去部分的宽度的关系如图乙所示,
当切去部分的宽度为10cm时,即B物体全部被切除时,A对地面的压强为4000Pa,
根据压强公式可知p1==,
代入数据得:4000Pa=,
故GA=160N;
根据G=mg可知A的质量mA===16kg,
根据密度公式可知A的密度ρA===2×103kg/m3;
(2)当切去部分的宽度为0cm时,即B物体没有被切除时,A对地面的压强为4250Pa,
根据压强公式可知:p2==,
代入数据得:4250Pa=,
据此得出B的重力GB=10N;
(3)由于A、B分别沿竖直方向按相同比例k截下一部分,并将截下的部分分别叠放在对方剩余部分上,则截下的部分对地面的压力分别为:
FA′=GA﹣kGA+kGB=(1﹣k)GA+kGB;
FB′=GB﹣kGB+kGA=(1﹣k)GB+kGA;
截下的部分对地面的受力面积分别为:
SA′=SA﹣kSA=(1﹣k)SA;
SB′=SB﹣kSB=(1﹣k)SB;
因为A、B剩余部分对水平地面的压强相同,即pA′=pB′,
所以,=,
即:=,
所以,+=+,
即:×(﹣)=﹣,
则:×(﹣)=﹣,
解得:k=。
答:(1)A物体的密度为2×103kg/m3;
(2)B物体的重力为10N;
(3)k的值为。
3.如图所示,底面积不同足够高的圆柱形容器甲、乙(S甲>S乙)置于水平地面上。
①若容器甲重为9.8牛,底面积为1×10﹣2米2,内部盛有深度为0.4米的水。求:
(a)水对容器甲底部的压强p水;
(b)容器甲对水平地面的压强p地。
②若容器甲、乙中的液体A、B对容器底部的压强相等。为使A液体对容器甲底部的压强大于B液体对容器乙底部的压强,有如下方案:(a)在容器甲、乙中同时抽取相同质量的液体;(b)在容器甲、乙中同时加入相同高度的原有液体。请分析每种方案的可行性。
【解答】解:(1)①水对容器甲底部的压强:p水=ρ水gh=1.0×103kg/m3×9.8N/kg×0.4m=3.92×103Pa;
②容器甲内水的体积:V水=S甲h水=1×10﹣2m2×0.4m=4×10﹣3m3;
水的质量:m水=ρ水V水=1.0×103kg/m3×4×10﹣3m3=4kg;
容器甲对水平地面的压力:F地=G水+G甲容=m水g+G甲容=4kg×9.8N/kg+9.8N=49N;
容器甲对地面的压强:p地===4900Pa;
(2)已知液体A、B对容器底部的压强 p甲=p乙;
两个容器是圆柱形的,液体对容器底的压力等于液体的重力,所以液体对容器底的压强:
p甲=;p乙=;
(a)在容器甲、乙中同时抽取相同质量的液体,设抽取液体的质量为m,则剩余液体对容器底的压强:
p甲剩==﹣=;
p乙剩==﹣=;
因为S甲>S乙 所以,p甲剩>p乙剩
此方案可行;
(b)已知液体A、B对容器底部的压强 p甲=p乙;且h甲>h乙;
由p=ρgh可知液体的密度关系 ρA<ρB;
在容器甲、乙中同时加入相同高度的原有液体,由p=ρgh可知增大的压强:
Δp甲<Δp乙;
加入液体后对容器底的压强:
p甲1=p甲+Δp甲;
p乙1=p乙+Δp乙;
所以p甲1<p乙1;
此方案不可行。
答:(1)水对容器甲底部的压强是3.92×103Pa;容器甲对水平地面的压强是4900Pa;
(2)(a)方案可行,(b)方案不可行。
4.如图所示,密度为2×103千克/米3、边长为0.1米均匀正方体甲和底面积为2×10﹣2米2的薄壁柱形容器乙放在水平地面上,乙容器足够高,内盛有0.1米深的水。
(1)求正方体甲的质量m甲。
(2)求水对乙容器底部的压强p乙。
(3)在甲的上部水平截去体积为V后,甲对水平地面的压强变为p甲′;将截取部分放入乙容器中,水对乙容器底部的压强变为p乙′,且p甲′=p乙′。试求水平截去体积V的大小。
【解答】解:(1)甲的体积:V甲=(0.1m)3=0.001m3;
由ρ=可得,正方体甲的质量:m甲=ρ甲V甲=2×103kg/m3×0.001m3=2kg;
(2)水对乙容器底部的压强:p=ρ水gh水=1.0×103kg/m3×10N/kg×0.1m=1000Pa;
(3)在甲的上部水平截去体积为V后,甲对水平地面的压强变为p甲′===,
因甲的密度大于水的密度,且截去体积的高度一定小于0.1m,放入水中后一定浸没在水中,水面上升的高度:Δh=,
则截取部分放入乙容器中,水对乙容器底部的压强变为p乙′=ρ水g(h水+Δh)=ρ水g(h水+),
已知p甲′=p乙′,
则有:=ρ水g(h水+),
代入数据可得:
=1.0×103kg/m3×10N/kg×(0.1m+)
解得:V=4×10﹣4m3。
答:(1)正方体甲的质量为2kg;
(2)水对乙容器底部的压强为1000Pa;
(3)水平截去体积为4×10﹣4m3。
二.液体的压强的计算(共6小题)
5.为了维护桃源沅水大桥,使用吊车向河底投放圆柱形混凝土构件如图甲所示,在整个投放过程中,混凝土构件以0.05m/s的速度匀速竖直下降。图乙是钢丝绳的拉力F随时间t变化的图像。当t=0s时吊车开始投放,混凝土构件到100s时结束,此时构件竖立在河中。(已知混凝土的密度为2.6×103kg/m3,钢铁的密度为7.8×103kg/m3,g取10N/kg,水的阻力可以忽略不计)求:
(1)混凝土构件的体积;
(2)投放结束时混凝土构件顶部受到水的压强;
(3)通过计算说明这种混凝土构件混凝土与钢筋的质量之比。
【解答】解:(1)由图象可以看出,当时间为t=50s时,浮力大小不再改变,此时混凝土构件完全浸没在水中,此时构件受到的浮力为:
F浮=G﹣F拉=1200N﹣800N=400N;
由F浮=ρgV排得构件的体积:
V=V排===0.04m3;
(2)由图象读出构件完全在水中下落的时间:t=100s﹣50s=50s,
由v=得顶部到水面的深度:
h=vt=0.05m/s×50s=2.5m,
顶部受到水的压强:
p=ρgh=1×103kg/m3×10N/kg×2.5m=2.5×104Pa;
(3)构件的质量为:m===120kg,
设构件中混凝土的质量为m1,钢筋的质量为m2,则有:
m1+m2=m﹣﹣﹣﹣①
根据ρ=可知,
+=V﹣﹣﹣﹣②
联立①②,代入数据解得:m1=96kg,m2=24kg,
则混凝土构件混凝土与钢筋的质量之比为:m1:m2=96kg:24kg=4:1。
答:(1)混凝土构件的体积为0.04m3;
(2)投放结束时混凝土构件顶部受到水的压强为2.5×104Pa;
(3)这种混凝土构件混凝土与钢筋的质量之比为4:1。
6.育才中学携手重庆机床集团打造了劳动教育社会实践基地,小明同学在基地加工了一个工件如图甲所示,由上下两个不同物质组成圆柱体连接在一起,上半部分A高10cm,底面积50cm2,其质量为400g,下半部分B为高10cm的正方体,B物质的密度为2g/cm3,另有一底面积200cm2,高13.5cm,重2N的圆柱形容器放在水平地面上,如图乙所示,内装2000cm3的水。小明想进一步研究激光切割技术,于是沿水平方向对工件进行切割,并将切割部分竖直放入水中冷却(不计水的汽化损失),则:
(1)未将工件放入水中时,水对容器底的压强是多少Pa?
(2)总共水平切去多少cm时,切割部分恰好在水中悬浮?
(3)某次切割后,工件剩会部分对地面压强能否和放入切制部分的容器对地面的压强相等?若能,请求出切去部分的高度;若不能,请通过计算说明理由。
【解答】解:(1)容器中水的深度为:h水===10cm=0.1m,
则未将工件放入水中时,水对容器底的压强为:
p=ρ水gh水=1.0×103kg/m3×10N/kg×0.1m=1.0×103Pa;
(2)物体A的体积VA=SAhA=50cm2×10cm=500cm3,
物体A受到的重力GA=mAg=0.4kg×10N/kg=4N,
物体A的密度ρA====0.8g/cm3,
物体B的体积VB=(LB)3=(10cm)3=1000cm3,
物体B的质量mB=ρBVB=2g/cm3×1000cm3=2000g=2kg,
物体B受到的重力GB=mBg=2kg×10N/kg=20N,
工件全部浸没在水中时,排开水的总体积为:
V排=V总=VA+VB=500cm3+1000cm3=1500cm3,
受到的浮力为:F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1500×10﹣6m3=15N,
所以,F浮<GA+GB=4N+20N=24N,
则工件放入水中会沉底,
又因为ρA<ρ水,所以若水平切去A,切割部分的密度小于水的密度,不会在水中悬浮,只会漂浮,故应水平切去B,
设从B底面向上切割的高度为h0,则切割部分的体积为:
V切=V总﹣VB0=V总+(LB)2×h0=1500cm3﹣100cm2×h0,
则切割部分的质量为:m切=mA+mB﹣×mB=400g+2000g﹣×2000g=2400g﹣200g×h0,
而切割部分在水中悬浮,则F浮'=G切,即:ρ水gV切=m切g,
则:ρ水V切=m切,1g/cm3×(1500cm3﹣100cm2×h0)=2400g﹣200g×h0,
解得:h0=9cm,
则切去的高度为:h=hA+LB﹣h0=10cm+10cm﹣9cm=11cm;
(3)假设能,设从B底面向上切割的高度为Δh,
则剩余部分的质量为:m剩=ρBV剩=ρBSBΔh,
则剩余部分对地面的压强为:p剩=====ρBΔhg,
而切割部分的质量为:m切'=mA+mB﹣m剩,
水受到的重力为:G水=m水g=ρ水V水g=1.0×103kg/m3×2000×10﹣6m3×10N/kg=20N,
则放入切制部分的容器对地面的压力为:F压=G水+G容+G切=20N+2N+(mA+mB﹣m剩)g=22N+(0.4kg+2kg﹣ρBSBΔh)g=46N﹣ρBSBΔhg,
则放入切制部分的容器对地面的压强为:p压==,
而p剩=p压,则:ρBΔhg=,
即:2×103kg/m3×Δh×10N/kg=,
解得:Δh=0.092m=9.2cm,
故沿水平方向切去部分的高度为:h'=hA+LB﹣Δh=10cm+10cm﹣9.2cm=10.8cm。
答:(1)未将工件放入水中时,水对容器底的压强是1.0×103Pa;
(2)总共水平切去11cm时,切割部分恰好在水中悬浮;
(3)某次切去10.8cm,工件剩会部分对地面压强和放入切制部分的容器对地面的压强相等。
7.如图所示,不吸水的长方体A固定在体积不计的轻杆下端,位于水平地面上的圆柱形容器内,杆上端固定不动。容器内盛有10cm深的水,物体下表面刚好与容器内的水面相平。往容器中缓慢注水,加水过程中水没有溢出。当加500cm3的水时,轻杆受力为6N,容器底部受到的压强较注水前变化了Δp1;当加2000cm3的水时,轻杆受力为3N,容器底部受到的压强较注水前变化了Δp2,且Δp1:Δp2=1:4.(ρ水=1.0×103kg/m3)求:
(1)加水前水对容器底的压强;
(2)加2000cm3的水时,加入水的质量;
(3)物块A的重力GA。
【解答】解:(1)加水前,水的深度为:h=10cm=0.1m,水对容器底的压强为:p水=ρ水gh=1.0×103kg/m3×10N/kg×0.1m=1000Pa;
(2)由ρ=可知,加2000cm3的水时,加入水的质量:Δm水2=ρ水V水2=1.0×103kg/m3×2000×10﹣6cm3=2kg;
(3)第二次轻杠受到的力为3N小于第一次轻杠受到的力为6N,说明第一次A未被浸没且所受浮力小于重力,第二次加水比第一次多,故第二次加水后长方体A受到的浮力比第一次大,轻杠对A有向上的拉力,则圆柱形容器底部受到的水的压力的增加量等于长方体A受到的浮力与加入水的重力之和,即ΔF1=ΔG水1+F浮=ΔG水1+GA﹣F拉1;第二次A所受浮力可能小于重力,轻杠对A可能有向上的拉力,或者浮力大于重力,轻杠对A有向下的压力,则圆柱形容器底部受到的水的压力的增加量等于长方体A受到的浮力与加入水的重力之和,即ΔF2=ΔG水2+F浮=ΔG水2+GA﹣F拉2,
或ΔF2=ΔG水2+F浮=ΔG水2+GA+F压,则:
第一次加入水的重力为:ΔG水1=Δm水1g=ρ水ΔV1g=1.0×103kg/m3×500×10﹣6m3×10N/kg=5N,
第一次压力变化量为:ΔF1=ΔG水1+GA﹣F拉1=GA+5N﹣6N=GA﹣1N
第二次加入水的重力为:ΔG水2=Δm水2g=2kg×10N/kg=20N,
第二次压力变化量为:ΔF2=ΔG水2+GA﹣F拉2=GA+20N﹣3N=GA+17N,或ΔF2=ΔG水2+GA+F压=GA+20N+3N=GA+23N;
因为Δp=,所以:
Δp1==……①
Δp2==……②
或Δp2==……③
Δp1:Δp2=1:4……④
由①②④解得:GA=7N,
由①③④解得:GA=9N。
答:(1)加水前水对容器底的压强为1000Pa;
(2)加2000cm3的水时,加入水的质量为2kg;
(3)物块A的重力GA为7N或9N。
8.如图所示,装有水的薄壁轻质圆柱形容器甲与圆柱形物块乙等高,放置于水平地面上,甲中水的深度为0.1米,底面积为0.02米2,求:
(1)水对容器底部的压强p水。
(2)容器内水的质量m水。
(3)若水的深度是容器高度的,甲的底面积是乙的2倍,乙的密度是水的3倍,现将乙
放入容器甲中,求:水对容器底的压强与容器对地面的压强的比值。
【解答】解:
(1)水对容器底部的压强:p水=ρ水gh=1.0×103kg/m3×10N/kg×0.1m=1000Pa;
(2)由ρ=和V=Sh可知,水的质量:m水=ρ水V水=ρ水Sh=1.0×103kg/m3×0.02m2×0.1m=2kg;
(3)乙的密度是水的3倍,则将乙放入容器甲中,由浮沉条件可知乙物块在水中会沉底,
假设乙物块在水中没有浸没(即有一部分露出水面),此时相当于水分布在物块的两侧,
设原来和现在水的深度分别为h水、h水′,
因容器中水的体积一定,则有:S甲h水=(S甲﹣S乙)h水′﹣﹣﹣﹣﹣①,已知S甲=2S乙﹣﹣﹣﹣﹣﹣﹣﹣②
联立①②解得h水′=2h水<H容器=3h水,故假设成立,也无水溢出;
此时水对容器底的压强:p水′=ρ水gh水′=2ρ水gh水﹣﹣﹣﹣﹣﹣③
容器中水的重力:G水=ρ水gV水=ρ水gS甲h水,
乙的密度是水的3倍,圆柱形容器甲与圆柱形物块乙等高(即h乙=H容器=3h水),
则圆柱体的重力:G乙=m乙g=ρ乙V乙g=ρ乙S乙h乙g=3ρ水×S甲×3h水×g=ρ水gS甲h水,
轻质容器的重力不计,则此时容器对地面的压强:
p容器′====ρ水gh水﹣﹣﹣﹣﹣﹣④
故水对容器底的压强与容器对地面的压强的比值为:
p水′:p容器′=2ρ水gh水:ρ水gh水=4:11。
答:(1)水对容器底部的压强为1000Pa。
(2)容器内水的质量为2kg。
(3)水对容器底的压强与容器对地面的压强的比值为4:11。
9.如图所示,足够高的薄壁圆柱形容器甲置于水平地面,容器底面积为3×10﹣2米2。其内部中央放置一个质量为2千克、体积为V0的物体乙。
液体 质量 密度
A m 2ρ
B 2m 2ρ
C 3m 4ρ
①求乙对容器底部的压力F乙。
②向容器中倒入0.1米深的水,求水对容器底部的压强p水。
③现有A、B、C三种液体,它们的质量、密度如表所示,请选择其中一种倒入容器中(物体均能浸没在液体中),使液体对容器底部的压力F液最大。写出选择的液体并说明理由,求出F液最大。
【解答】解:①乙对容器底部的压力:F乙=G乙=m乙g=2kg×10N/kg=20N;
②向容器中倒入0.1米深的水,水对容器底部的压强:p水=ρ水gh=l×103kg/m3×10N/kg×0.1m=1×103Pa;
③a、当A液体倒入容器后,容器内液体的深度:h1===+,
此时液体对容器底部的压强:p液A=ρAgh1=2ρg(+)=ρgV0+mg;
b、同理,当B液体倒入容器后,容器内液体的深度:h2===+,
此时液体对容器底部的压强:p液B=ρBgh2=2ρg(+)=ρgV0+mg;
c、同理,当C液体倒入容器后,容器内液体的深度:h3===+,
此时液体对容器底部的压强:p液C=ρcgh3=4ρg(+)=ρgV0+100mg;
比较A、B、C液体对容器底部的压强可知:
p液C>p液B>p液A,
由F=pS可知,倒入液体C时,液体对容器底部的压强最大,最大压力:F液最大=p液CS=(ρgV0+100mg)×3×10﹣2m2=4ρgV0+3mg。
答:(1)乙对容器底部的压力是20N;
(2)水对容器底部的压强是1×103Pa;
(3)倒入液体C时,液体对容器底部的压力F液最大,最大压力是4ρgV0+3mg。
10.如图所示,足够高的圆柱形薄底容器A、B置于水平地面上,分别盛有水和液体乙。容器A的底面积为250cm2,水的重力为20N,两容器底部受到液体的压强相等。求:(g取10N/kg,水的密度ρ水=1.0×103kg/m3)。
(1)水的体积V水;
(2)水对容器A底部的压强p水;
(3)在容器A中注入水,使两容器中液面相平,此时水对容器A底部的压强增加了200Pa,求液体乙的密度ρ乙。
【解答】解:(1)容器甲中水的质量为:m水===2kg,
水的体积为:V水===2×10﹣3m3;
(2)容器甲中水的深度:h===0.08m,
水对容器底部的压强:p水=ρgh=1.0×103kg/m3×10N/kg×0.08m=800Pa。
(3)当容器甲内加水至于容器乙相平时,此时水深为h1,
此时水对容器底部的压强:p1=p水+Δp=800Pa+200Pa=1000Pa;
由p=ρgh可得此时水的深度:h1===0.1m;
由题知,原来容器甲、乙底部所受液体的压强相等,即:p乙=p水=800Pa;
由p=ρgh可得,液体乙的密度:ρ乙===800kg/m3。
答:(1)水的体积为2×10﹣3m3;
(2)容器甲中水对容器底部的压强为800Pa;
(3)液体乙的密度为800kg/m3。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
初中物理压强综合题练习
一.压强的大小及其计算(共4小题)
1.如图,实心圆柱体甲、乙的密度均为3×103kg/m3,甲的质量为6kg,底面积为200cm2,乙的质量为12kg,底面积为300cm2。水平地面上的轻质薄壁容器丙内盛有9cm深的水,容器上部分高度为下部分高度的五分之一,容器下底面积为1000cm2。若把甲沿水平方向切割Δh的高度,切割下来的部分竖直缓慢浸没在丙容器的水中,液面的上升高度Δh水与切割的高度Δh的部分关系如图丁所示。求:
(1)圆柱体甲的体积V甲;
(2)容器丙中水的重力;
(3)若将圆柱体乙放入原装有9cm深水的容器丙中,此时容器丙对水平地面的压强。
2.A、B两物体均为质量分布均匀的实心正方体,A物体放在水平地面上,将B物体叠放在A物体上,如图甲所示。若沿竖直方向将B物体切去一部分,A对地面的压强与切去部分的宽度的关系如图乙所示,已知A、B物体的边长分别为20cm、10cm。求:
(1)A物体的密度;
(2)B物体的重力;
(3)现将A、B两物体分别置于水平地面上,如图丙所示。在正方体A、B上沿竖直方向按相同比例k截下一部分,并将截下的部分分别叠放在对方剩余部分上,若叠放后A、B剩余部分对水平地面的压强相等,则k的值为多少?
3.如图所示,底面积不同足够高的圆柱形容器甲、乙(S甲>S乙)置于水平地面上。
①若容器甲重为9.8牛,底面积为1×10﹣2米2,内部盛有深度为0.4米的水。求:
(a)水对容器甲底部的压强p水;
(b)容器甲对水平地面的压强p地。
②若容器甲、乙中的液体A、B对容器底部的压强相等。为使A液体对容器甲底部的压强大于B液体对容器乙底部的压强,有如下方案:(a)在容器甲、乙中同时抽取相同质量的液体;(b)在容器甲、乙中同时加入相同高度的原有液体。请分析每种方案的可行性。
4.如图所示,密度为2×103千克/米3、边长为0.1米均匀正方体甲和底面积为2×10﹣2米2的薄壁柱形容器乙放在水平地面上,乙容器足够高,内盛有0.1米深的水。
(1)求正方体甲的质量m甲。
(2)求水对乙容器底部的压强p乙。
(3)在甲的上部水平截去体积为V后,甲对水平地面的压强变为p甲′;将截取部分放入乙容器中,水对乙容器底部的压强变为p乙′,且p甲′=p乙′。试求水平截去体积V的大小。
二.液体的压强的计算(共6小题)
5.为了维护桃源沅水大桥,使用吊车向河底投放圆柱形混凝土构件如图甲所示,在整个投放过程中,混凝土构件以0.05m/s的速度匀速竖直下降。图乙是钢丝绳的拉力F随时间t变化的图像。当t=0s时吊车开始投放,混凝土构件到100s时结束,此时构件竖立在河中。(已知混凝土的密度为2.6×103kg/m3,钢铁的密度为7.8×103kg/m3,g取10N/kg,水的阻力可以忽略不计)求:
(1)混凝土构件的体积;
(2)投放结束时混凝土构件顶部受到水的压强;
(3)通过计算说明这种混凝土构件混凝土与钢筋的质量之比。
6.育才中学携手重庆机床集团打造了劳动教育社会实践基地,小明同学在基地加工了一个工件如图甲所示,由上下两个不同物质组成圆柱体连接在一起,上半部分A高10cm,底面积50cm2,其质量为400g,下半部分B为高10cm的正方体,B物质的密度为2g/cm3,另有一底面积200cm2,高13.5cm,重2N的圆柱形容器放在水平地面上,如图乙所示,内装2000cm3的水。小明想进一步研究激光切割技术,于是沿水平方向对工件进行切割,并将切割部分竖直放入水中冷却(不计水的汽化损失),则:
(1)未将工件放入水中时,水对容器底的压强是多少Pa?
(2)总共水平切去多少cm时,切割部分恰好在水中悬浮?
(3)某次切割后,工件剩会部分对地面压强能否和放入切制部分的容器对地面的压强相等?若能,请求出切去部分的高度;若不能,请通过计算说明理由。
7.如图所示,不吸水的长方体A固定在体积不计的轻杆下端,位于水平地面上的圆柱形容器内,杆上端固定不动。容器内盛有10cm深的水,物体下表面刚好与容器内的水面相平。往容器中缓慢注水,加水过程中水没有溢出。当加500cm3的水时,轻杆受力为6N,容器底部受到的压强较注水前变化了Δp1;当加2000cm3的水时,轻杆受力为3N,容器底部受到的压强较注水前变化了Δp2,且Δp1:Δp2=1:4.(ρ水=1.0×103kg/m3)求:
(1)加水前水对容器底的压强;
(2)加2000cm3的水时,加入水的质量;
(3)物块A的重力GA。
8.如图所示,装有水的薄壁轻质圆柱形容器甲与圆柱形物块乙等高,放置于水平地面上,甲中水的深度为0.1米,底面积为0.02米2,求:
(1)水对容器底部的压强p水。
(2)容器内水的质量m水。
(3)若水的深度是容器高度的,甲的底面积是乙的2倍,乙的密度是水的3倍,现将乙
放入容器甲中,求:水对容器底的压强与容器对地面的压强的比值。
9.如图所示,足够高的薄壁圆柱形容器甲置于水平地面,容器底面积为3×10﹣2米2。其内部中央放置一个质量为2千克、体积为V0的物体乙。
液体 质量 密度
A m 2ρ
B 2m 2ρ
C 3m 4ρ
①求乙对容器底部的压力F乙。
②向容器中倒入0.1米深的水,求水对容器底部的压强p水。
③现有A、B、C三种液体,它们的质量、密度如表所示,请选择其中一种倒入容器中(物体均能浸没在液体中),使液体对容器底部的压力F液最大。写出选择的液体并说明理由,求出F液最大。
10.如图所示,足够高的圆柱形薄底容器A、B置于水平地面上,分别盛有水和液体乙。容器A的底面积为250cm2,水的重力为20N,两容器底部受到液体的压强相等。求:(g取10N/kg,水的密度ρ水=1.0×103kg/m3)。
(1)水的体积V水;
(2)水对容器A底部的压强p水;
(3)在容器A中注入水,使两容器中液面相平,此时水对容器A底部的压强增加了200Pa,求液体乙的密度ρ乙。
参考答案与试题解析
一.压强的大小及其计算(共4小题)
1.如图,实心圆柱体甲、乙的密度均为3×103kg/m3,甲的质量为6kg,底面积为200cm2,乙的质量为12kg,底面积为300cm2。水平地面上的轻质薄壁容器丙内盛有9cm深的水,容器上部分高度为下部分高度的五分之一,容器下底面积为1000cm2。若把甲沿水平方向切割Δh的高度,切割下来的部分竖直缓慢浸没在丙容器的水中,液面的上升高度Δh水与切割的高度Δh的部分关系如图丁所示。求:
(1)圆柱体甲的体积V甲;
(2)容器丙中水的重力;
(3)若将圆柱体乙放入原装有9cm深水的容器丙中,此时容器丙对水平地面的压强。
【解答】解:(1)根据题意,由密度公式ρ=可得甲的体积为V甲=;
(2)容器中水的质量为m水=ρ水V水=1.0g/cm3×9cm×1000cm2=9000g=9kg;
由重力计算公式G=mg可得容器中水的重力为G水=m水g=9kg×10N/kg=90N;
(3)根据题意,由丁图可知,Δh=5cm时,Δh水=lcm,然后Δh水上升更快,表明其底面积减小了,所以容器下部分的高度为h下=9cm+lcm=10cm,则上部分的高度为h上==×10cm=2cm;
根据丁图可知,当Δh=5cm,Δh水=lcm时刚好是上下部分的分界线,而水上升的体积等于甲浸没在水中的体积,则有Δh'水S丙上=Δh'S甲;
则容器丙上部分的底面积为S丙上=;
将乙放入丙内时,下部分装有水的体积为V下=(S丙下﹣S乙)h下=( 1000cm2﹣300cm2)×10cm=7000cm3;
所以剩余的水的体积为V余=V水﹣V下=1000cm2×9cm﹣7000cm3=2000cm3;
而将乙放入丙内时,上部分能装的水的体积为V上=(S丙上﹣S乙)h上=(500cm2﹣300cm2)×2cm=400cm3;
由于V余>V上,所以上部分的水的体积为V上=400cm3,其余溢出了,
故容器丙中剩余水的总质量为m′水=(7000cm3+400cm3)×1.0g/cm3=7400g=7.4kg
所以将乙放入丙内时,对水平面的压力等于总重力,即F=G总=(7.4kg+12kg)×10N/kg=194N;
根据压强的公式p=可得:对水平面的压强为p=;
答:(1)圆柱体甲的体积为2×10﹣3m3;
(2)容器丙中水的重力为90N;
(3)容器丙对水平地面的压强为1940Pa。
2.A、B两物体均为质量分布均匀的实心正方体,A物体放在水平地面上,将B物体叠放在A物体上,如图甲所示。若沿竖直方向将B物体切去一部分,A对地面的压强与切去部分的宽度的关系如图乙所示,已知A、B物体的边长分别为20cm、10cm。求:
(1)A物体的密度;
(2)B物体的重力;
(3)现将A、B两物体分别置于水平地面上,如图丙所示。在正方体A、B上沿竖直方向按相同比例k截下一部分,并将截下的部分分别叠放在对方剩余部分上,若叠放后A、B剩余部分对水平地面的压强相等,则k的值为多少?
【解答】解:(1)A的边长LA=20cm=0.2m,
B的边长LB=10cm=0.1m,
A的底面积SA=LA2=(0.2m)2=0.04m2,
B的底面积SB=LB2=(0.1m)2=0.01m2,
A对地面的压强与切去部分的宽度的关系如图乙所示,
当切去部分的宽度为10cm时,即B物体全部被切除时,A对地面的压强为4000Pa,
根据压强公式可知p1==,
代入数据得:4000Pa=,
故GA=160N;
根据G=mg可知A的质量mA===16kg,
根据密度公式可知A的密度ρA===2×103kg/m3;
(2)当切去部分的宽度为0cm时,即B物体没有被切除时,A对地面的压强为4250Pa,
根据压强公式可知:p2==,
代入数据得:4250Pa=,
据此得出B的重力GB=10N;
(3)由于A、B分别沿竖直方向按相同比例k截下一部分,并将截下的部分分别叠放在对方剩余部分上,则截下的部分对地面的压力分别为:
FA′=GA﹣kGA+kGB=(1﹣k)GA+kGB;
FB′=GB﹣kGB+kGA=(1﹣k)GB+kGA;
截下的部分对地面的受力面积分别为:
SA′=SA﹣kSA=(1﹣k)SA;
SB′=SB﹣kSB=(1﹣k)SB;
因为A、B剩余部分对水平地面的压强相同,即pA′=pB′,
所以,=,
即:=,
所以,+=+,
即:×(﹣)=﹣,
则:×(﹣)=﹣,
解得:k=。
答:(1)A物体的密度为2×103kg/m3;
(2)B物体的重力为10N;
(3)k的值为。
3.如图所示,底面积不同足够高的圆柱形容器甲、乙(S甲>S乙)置于水平地面上。
①若容器甲重为9.8牛,底面积为1×10﹣2米2,内部盛有深度为0.4米的水。求:
(a)水对容器甲底部的压强p水;
(b)容器甲对水平地面的压强p地。
②若容器甲、乙中的液体A、B对容器底部的压强相等。为使A液体对容器甲底部的压强大于B液体对容器乙底部的压强,有如下方案:(a)在容器甲、乙中同时抽取相同质量的液体;(b)在容器甲、乙中同时加入相同高度的原有液体。请分析每种方案的可行性。
【解答】解:(1)①水对容器甲底部的压强:p水=ρ水gh=1.0×103kg/m3×9.8N/kg×0.4m=3.92×103Pa;
②容器甲内水的体积:V水=S甲h水=1×10﹣2m2×0.4m=4×10﹣3m3;
水的质量:m水=ρ水V水=1.0×103kg/m3×4×10﹣3m3=4kg;
容器甲对水平地面的压力:F地=G水+G甲容=m水g+G甲容=4kg×9.8N/kg+9.8N=49N;
容器甲对地面的压强:p地===4900Pa;
(2)已知液体A、B对容器底部的压强 p甲=p乙;
两个容器是圆柱形的,液体对容器底的压力等于液体的重力,所以液体对容器底的压强:
p甲=;p乙=;
(a)在容器甲、乙中同时抽取相同质量的液体,设抽取液体的质量为m,则剩余液体对容器底的压强:
p甲剩==﹣=;
p乙剩==﹣=;
因为S甲>S乙 所以,p甲剩>p乙剩
此方案可行;
(b)已知液体A、B对容器底部的压强 p甲=p乙;且h甲>h乙;
由p=ρgh可知液体的密度关系 ρA<ρB;
在容器甲、乙中同时加入相同高度的原有液体,由p=ρgh可知增大的压强:
Δp甲<Δp乙;
加入液体后对容器底的压强:
p甲1=p甲+Δp甲;
p乙1=p乙+Δp乙;
所以p甲1<p乙1;
此方案不可行。
答:(1)水对容器甲底部的压强是3.92×103Pa;容器甲对水平地面的压强是4900Pa;
(2)(a)方案可行,(b)方案不可行。
4.如图所示,密度为2×103千克/米3、边长为0.1米均匀正方体甲和底面积为2×10﹣2米2的薄壁柱形容器乙放在水平地面上,乙容器足够高,内盛有0.1米深的水。
(1)求正方体甲的质量m甲。
(2)求水对乙容器底部的压强p乙。
(3)在甲的上部水平截去体积为V后,甲对水平地面的压强变为p甲′;将截取部分放入乙容器中,水对乙容器底部的压强变为p乙′,且p甲′=p乙′。试求水平截去体积V的大小。
【解答】解:(1)甲的体积:V甲=(0.1m)3=0.001m3;
由ρ=可得,正方体甲的质量:m甲=ρ甲V甲=2×103kg/m3×0.001m3=2kg;
(2)水对乙容器底部的压强:p=ρ水gh水=1.0×103kg/m3×10N/kg×0.1m=1000Pa;
(3)在甲的上部水平截去体积为V后,甲对水平地面的压强变为p甲′===,
因甲的密度大于水的密度,且截去体积的高度一定小于0.1m,放入水中后一定浸没在水中,水面上升的高度:Δh=,
则截取部分放入乙容器中,水对乙容器底部的压强变为p乙′=ρ水g(h水+Δh)=ρ水g(h水+),
已知p甲′=p乙′,
则有:=ρ水g(h水+),
代入数据可得:
=1.0×103kg/m3×10N/kg×(0.1m+)
解得:V=4×10﹣4m3。
答:(1)正方体甲的质量为2kg;
(2)水对乙容器底部的压强为1000Pa;
(3)水平截去体积为4×10﹣4m3。
二.液体的压强的计算(共6小题)
5.为了维护桃源沅水大桥,使用吊车向河底投放圆柱形混凝土构件如图甲所示,在整个投放过程中,混凝土构件以0.05m/s的速度匀速竖直下降。图乙是钢丝绳的拉力F随时间t变化的图像。当t=0s时吊车开始投放,混凝土构件到100s时结束,此时构件竖立在河中。(已知混凝土的密度为2.6×103kg/m3,钢铁的密度为7.8×103kg/m3,g取10N/kg,水的阻力可以忽略不计)求:
(1)混凝土构件的体积;
(2)投放结束时混凝土构件顶部受到水的压强;
(3)通过计算说明这种混凝土构件混凝土与钢筋的质量之比。
【解答】解:(1)由图象可以看出,当时间为t=50s时,浮力大小不再改变,此时混凝土构件完全浸没在水中,此时构件受到的浮力为:
F浮=G﹣F拉=1200N﹣800N=400N;
由F浮=ρgV排得构件的体积:
V=V排===0.04m3;
(2)由图象读出构件完全在水中下落的时间:t=100s﹣50s=50s,
由v=得顶部到水面的深度:
h=vt=0.05m/s×50s=2.5m,
顶部受到水的压强:
p=ρgh=1×103kg/m3×10N/kg×2.5m=2.5×104Pa;
(3)构件的质量为:m===120kg,
设构件中混凝土的质量为m1,钢筋的质量为m2,则有:
m1+m2=m﹣﹣﹣﹣①
根据ρ=可知,
+=V﹣﹣﹣﹣②
联立①②,代入数据解得:m1=96kg,m2=24kg,
则混凝土构件混凝土与钢筋的质量之比为:m1:m2=96kg:24kg=4:1。
答:(1)混凝土构件的体积为0.04m3;
(2)投放结束时混凝土构件顶部受到水的压强为2.5×104Pa;
(3)这种混凝土构件混凝土与钢筋的质量之比为4:1。
6.育才中学携手重庆机床集团打造了劳动教育社会实践基地,小明同学在基地加工了一个工件如图甲所示,由上下两个不同物质组成圆柱体连接在一起,上半部分A高10cm,底面积50cm2,其质量为400g,下半部分B为高10cm的正方体,B物质的密度为2g/cm3,另有一底面积200cm2,高13.5cm,重2N的圆柱形容器放在水平地面上,如图乙所示,内装2000cm3的水。小明想进一步研究激光切割技术,于是沿水平方向对工件进行切割,并将切割部分竖直放入水中冷却(不计水的汽化损失),则:
(1)未将工件放入水中时,水对容器底的压强是多少Pa?
(2)总共水平切去多少cm时,切割部分恰好在水中悬浮?
(3)某次切割后,工件剩会部分对地面压强能否和放入切制部分的容器对地面的压强相等?若能,请求出切去部分的高度;若不能,请通过计算说明理由。
【解答】解:(1)容器中水的深度为:h水===10cm=0.1m,
则未将工件放入水中时,水对容器底的压强为:
p=ρ水gh水=1.0×103kg/m3×10N/kg×0.1m=1.0×103Pa;
(2)物体A的体积VA=SAhA=50cm2×10cm=500cm3,
物体A受到的重力GA=mAg=0.4kg×10N/kg=4N,
物体A的密度ρA====0.8g/cm3,
物体B的体积VB=(LB)3=(10cm)3=1000cm3,
物体B的质量mB=ρBVB=2g/cm3×1000cm3=2000g=2kg,
物体B受到的重力GB=mBg=2kg×10N/kg=20N,
工件全部浸没在水中时,排开水的总体积为:
V排=V总=VA+VB=500cm3+1000cm3=1500cm3,
受到的浮力为:F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1500×10﹣6m3=15N,
所以,F浮<GA+GB=4N+20N=24N,
则工件放入水中会沉底,
又因为ρA<ρ水,所以若水平切去A,切割部分的密度小于水的密度,不会在水中悬浮,只会漂浮,故应水平切去B,
设从B底面向上切割的高度为h0,则切割部分的体积为:
V切=V总﹣VB0=V总+(LB)2×h0=1500cm3﹣100cm2×h0,
则切割部分的质量为:m切=mA+mB﹣×mB=400g+2000g﹣×2000g=2400g﹣200g×h0,
而切割部分在水中悬浮,则F浮'=G切,即:ρ水gV切=m切g,
则:ρ水V切=m切,1g/cm3×(1500cm3﹣100cm2×h0)=2400g﹣200g×h0,
解得:h0=9cm,
则切去的高度为:h=hA+LB﹣h0=10cm+10cm﹣9cm=11cm;
(3)假设能,设从B底面向上切割的高度为Δh,
则剩余部分的质量为:m剩=ρBV剩=ρBSBΔh,
则剩余部分对地面的压强为:p剩=====ρBΔhg,
而切割部分的质量为:m切'=mA+mB﹣m剩,
水受到的重力为:G水=m水g=ρ水V水g=1.0×103kg/m3×2000×10﹣6m3×10N/kg=20N,
则放入切制部分的容器对地面的压力为:F压=G水+G容+G切=20N+2N+(mA+mB﹣m剩)g=22N+(0.4kg+2kg﹣ρBSBΔh)g=46N﹣ρBSBΔhg,
则放入切制部分的容器对地面的压强为:p压==,
而p剩=p压,则:ρBΔhg=,
即:2×103kg/m3×Δh×10N/kg=,
解得:Δh=0.092m=9.2cm,
故沿水平方向切去部分的高度为:h'=hA+LB﹣Δh=10cm+10cm﹣9.2cm=10.8cm。
答:(1)未将工件放入水中时,水对容器底的压强是1.0×103Pa;
(2)总共水平切去11cm时,切割部分恰好在水中悬浮;
(3)某次切去10.8cm,工件剩会部分对地面压强和放入切制部分的容器对地面的压强相等。
7.如图所示,不吸水的长方体A固定在体积不计的轻杆下端,位于水平地面上的圆柱形容器内,杆上端固定不动。容器内盛有10cm深的水,物体下表面刚好与容器内的水面相平。往容器中缓慢注水,加水过程中水没有溢出。当加500cm3的水时,轻杆受力为6N,容器底部受到的压强较注水前变化了Δp1;当加2000cm3的水时,轻杆受力为3N,容器底部受到的压强较注水前变化了Δp2,且Δp1:Δp2=1:4.(ρ水=1.0×103kg/m3)求:
(1)加水前水对容器底的压强;
(2)加2000cm3的水时,加入水的质量;
(3)物块A的重力GA。
【解答】解:(1)加水前,水的深度为:h=10cm=0.1m,水对容器底的压强为:p水=ρ水gh=1.0×103kg/m3×10N/kg×0.1m=1000Pa;
(2)由ρ=可知,加2000cm3的水时,加入水的质量:Δm水2=ρ水V水2=1.0×103kg/m3×2000×10﹣6cm3=2kg;
(3)第二次轻杠受到的力为3N小于第一次轻杠受到的力为6N,说明第一次A未被浸没且所受浮力小于重力,第二次加水比第一次多,故第二次加水后长方体A受到的浮力比第一次大,轻杠对A有向上的拉力,则圆柱形容器底部受到的水的压力的增加量等于长方体A受到的浮力与加入水的重力之和,即ΔF1=ΔG水1+F浮=ΔG水1+GA﹣F拉1;第二次A所受浮力可能小于重力,轻杠对A可能有向上的拉力,或者浮力大于重力,轻杠对A有向下的压力,则圆柱形容器底部受到的水的压力的增加量等于长方体A受到的浮力与加入水的重力之和,即ΔF2=ΔG水2+F浮=ΔG水2+GA﹣F拉2,
或ΔF2=ΔG水2+F浮=ΔG水2+GA+F压,则:
第一次加入水的重力为:ΔG水1=Δm水1g=ρ水ΔV1g=1.0×103kg/m3×500×10﹣6m3×10N/kg=5N,
第一次压力变化量为:ΔF1=ΔG水1+GA﹣F拉1=GA+5N﹣6N=GA﹣1N
第二次加入水的重力为:ΔG水2=Δm水2g=2kg×10N/kg=20N,
第二次压力变化量为:ΔF2=ΔG水2+GA﹣F拉2=GA+20N﹣3N=GA+17N,或ΔF2=ΔG水2+GA+F压=GA+20N+3N=GA+23N;
因为Δp=,所以:
Δp1==……①
Δp2==……②
或Δp2==……③
Δp1:Δp2=1:4……④
由①②④解得:GA=7N,
由①③④解得:GA=9N。
答:(1)加水前水对容器底的压强为1000Pa;
(2)加2000cm3的水时,加入水的质量为2kg;
(3)物块A的重力GA为7N或9N。
8.如图所示,装有水的薄壁轻质圆柱形容器甲与圆柱形物块乙等高,放置于水平地面上,甲中水的深度为0.1米,底面积为0.02米2,求:
(1)水对容器底部的压强p水。
(2)容器内水的质量m水。
(3)若水的深度是容器高度的,甲的底面积是乙的2倍,乙的密度是水的3倍,现将乙
放入容器甲中,求:水对容器底的压强与容器对地面的压强的比值。
【解答】解:
(1)水对容器底部的压强:p水=ρ水gh=1.0×103kg/m3×10N/kg×0.1m=1000Pa;
(2)由ρ=和V=Sh可知,水的质量:m水=ρ水V水=ρ水Sh=1.0×103kg/m3×0.02m2×0.1m=2kg;
(3)乙的密度是水的3倍,则将乙放入容器甲中,由浮沉条件可知乙物块在水中会沉底,
假设乙物块在水中没有浸没(即有一部分露出水面),此时相当于水分布在物块的两侧,
设原来和现在水的深度分别为h水、h水′,
因容器中水的体积一定,则有:S甲h水=(S甲﹣S乙)h水′﹣﹣﹣﹣﹣①,已知S甲=2S乙﹣﹣﹣﹣﹣﹣﹣﹣②
联立①②解得h水′=2h水<H容器=3h水,故假设成立,也无水溢出;
此时水对容器底的压强:p水′=ρ水gh水′=2ρ水gh水﹣﹣﹣﹣﹣﹣③
容器中水的重力:G水=ρ水gV水=ρ水gS甲h水,
乙的密度是水的3倍,圆柱形容器甲与圆柱形物块乙等高(即h乙=H容器=3h水),
则圆柱体的重力:G乙=m乙g=ρ乙V乙g=ρ乙S乙h乙g=3ρ水×S甲×3h水×g=ρ水gS甲h水,
轻质容器的重力不计,则此时容器对地面的压强:
p容器′====ρ水gh水﹣﹣﹣﹣﹣﹣④
故水对容器底的压强与容器对地面的压强的比值为:
p水′:p容器′=2ρ水gh水:ρ水gh水=4:11。
答:(1)水对容器底部的压强为1000Pa。
(2)容器内水的质量为2kg。
(3)水对容器底的压强与容器对地面的压强的比值为4:11。
9.如图所示,足够高的薄壁圆柱形容器甲置于水平地面,容器底面积为3×10﹣2米2。其内部中央放置一个质量为2千克、体积为V0的物体乙。
液体 质量 密度
A m 2ρ
B 2m 2ρ
C 3m 4ρ
①求乙对容器底部的压力F乙。
②向容器中倒入0.1米深的水,求水对容器底部的压强p水。
③现有A、B、C三种液体,它们的质量、密度如表所示,请选择其中一种倒入容器中(物体均能浸没在液体中),使液体对容器底部的压力F液最大。写出选择的液体并说明理由,求出F液最大。
【解答】解:①乙对容器底部的压力:F乙=G乙=m乙g=2kg×10N/kg=20N;
②向容器中倒入0.1米深的水,水对容器底部的压强:p水=ρ水gh=l×103kg/m3×10N/kg×0.1m=1×103Pa;
③a、当A液体倒入容器后,容器内液体的深度:h1===+,
此时液体对容器底部的压强:p液A=ρAgh1=2ρg(+)=ρgV0+mg;
b、同理,当B液体倒入容器后,容器内液体的深度:h2===+,
此时液体对容器底部的压强:p液B=ρBgh2=2ρg(+)=ρgV0+mg;
c、同理,当C液体倒入容器后,容器内液体的深度:h3===+,
此时液体对容器底部的压强:p液C=ρcgh3=4ρg(+)=ρgV0+100mg;
比较A、B、C液体对容器底部的压强可知:
p液C>p液B>p液A,
由F=pS可知,倒入液体C时,液体对容器底部的压强最大,最大压力:F液最大=p液CS=(ρgV0+100mg)×3×10﹣2m2=4ρgV0+3mg。
答:(1)乙对容器底部的压力是20N;
(2)水对容器底部的压强是1×103Pa;
(3)倒入液体C时,液体对容器底部的压力F液最大,最大压力是4ρgV0+3mg。
10.如图所示,足够高的圆柱形薄底容器A、B置于水平地面上,分别盛有水和液体乙。容器A的底面积为250cm2,水的重力为20N,两容器底部受到液体的压强相等。求:(g取10N/kg,水的密度ρ水=1.0×103kg/m3)。
(1)水的体积V水;
(2)水对容器A底部的压强p水;
(3)在容器A中注入水,使两容器中液面相平,此时水对容器A底部的压强增加了200Pa,求液体乙的密度ρ乙。
【解答】解:(1)容器甲中水的质量为:m水===2kg,
水的体积为:V水===2×10﹣3m3;
(2)容器甲中水的深度:h===0.08m,
水对容器底部的压强:p水=ρgh=1.0×103kg/m3×10N/kg×0.08m=800Pa。
(3)当容器甲内加水至于容器乙相平时,此时水深为h1,
此时水对容器底部的压强:p1=p水+Δp=800Pa+200Pa=1000Pa;
由p=ρgh可得此时水的深度:h1===0.1m;
由题知,原来容器甲、乙底部所受液体的压强相等,即:p乙=p水=800Pa;
由p=ρgh可得,液体乙的密度:ρ乙===800kg/m3。
答:(1)水的体积为2×10﹣3m3;
(2)容器甲中水对容器底部的压强为800Pa;
(3)液体乙的密度为800kg/m3。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
