南京市2012-2013学年度第一学期期末调研测试高二数学试卷(文科)
文档属性
| 名称 | 南京市2012-2013学年度第一学期期末调研测试高二数学试卷(文科) |  | |
| 格式 | zip | ||
| 文件大小 | 28.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-02 16:04:47 | ||
图片预览



文档简介
南京市2012-2013学年度第一学期期末调研测试
高二数学试卷(文科) 2013.01
注意事项:
1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为100分,考试时间为100分钟.
2.答题前,请务必将自己的姓名、学校、班级、学号写在答卷纸的密封线内.试题的答案写在答卷纸上对应题目的答案空格内.考试结束后,交回答卷纸.
参考公式:V锥体=Sh (S表示底面面积,h表示锥体的高).
一、填空题:本大题共14小题,每小题3分,共42分.请把答案填写在答卷纸相应位置上
1.复数1-2i (i为虚数单位)在复平面内对应的点位于第 ▲ 象限.
2.已知命题p:(x∈R,x2>x-1,则(p为 ▲ .
3.在平面直角坐标系中,准线方程为y=4的抛物线标准的方程为 ▲ .
4.若复数z=4+3i (i为虚数单位),则|z |= ▲ .
5.双曲线x2-=1的渐近线方程为 ▲ .
6.“x>1”是“x>0”成立的 ▲ 条件(在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选出一种).
7.已知曲线y=ax2在x=1处切线的斜率是-4,则实数a的值为 ▲ .
8.若圆x2+y2=4与圆x2+(y-3)2=r2 (r>0)外切,则实数r的值为 ▲ .
9.函数y=x3-3x2+1的单调递减区间为 ▲ .
10.若直线3x+4y-12=0与圆(x-3)2+(y-2)2=4相交于M,N两点,则线段MN的长为 ▲ ..
11.观察下列等式:
=(-)×,
=(-)×,
=(-)×,
=(-)×,
………………
可推测当n≥3,n∈N*时,= ▲ .
12.已知椭圆+=1与双曲线—y2=1有共同焦点F1,F2,点P是两曲线的一个交点,
则PF1·PF2= ▲ .
13.在直角三角形ABC中,∠C为直角,两直角边长分别为a,b,求其外接圆半径时,可采取如下方法:将三角形ABC补成以其两直角边为邻边的矩形,则矩形的对角线为三角形外接圆的直径,可得三角形外接圆半径为;按此方法,在三棱锥S-ABC中,三条侧棱两两互相垂直,且长度分别为a,b,c,通过类比可得三棱锥S-ABC外接球的半径为 ▲ .
14.若函数f(x)在定义域D内某区间I上是增函数,且在I上是减函数,则称y=f(x)在I 上是“弱
增函数”.已知函数h(x)=x2-(b-1)x+b在(0,1]上是“弱增函数”,则实数b的值为 ▲ .
二、解答题:本大题共6小题,共计58分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本题满分8分)
已知复数z1满足z1·i=1+i (i为虚数单位),复数z2的虚部为2.
(1)求z1;
(2)若z1·z2是纯虚数,求z2.
16.(本题满分8分)
已知命题p:任意x∈R,x2+1≥a,命题q:方程-=1表示双曲线.
(1)若命题p为真命题,求实数a的取值范围;
(2)若 “p且q”为真命题,求实数a的取值范围.
17.(本题满分10分)
已知以点P为圆心的圆经过点A(1,4),B(3,6),线段AB的垂直平分线与圆P交于点
C,D,且CD=4.
(1)求直线CD的方程;
(2)求圆P的方程.
18.(本题满分10分)
如图,已知椭圆C:+=1(a>b>0)的右焦点为F(c,0),下顶点为A(0,-b),直线AF
与椭圆的右准线交于点B,若F恰好为线段AB的中点.
(1)求椭圆C的离心率;
(2)若直线AB与圆x2+y2=2相切,求椭圆C的方程.
19.(本题满分10分)
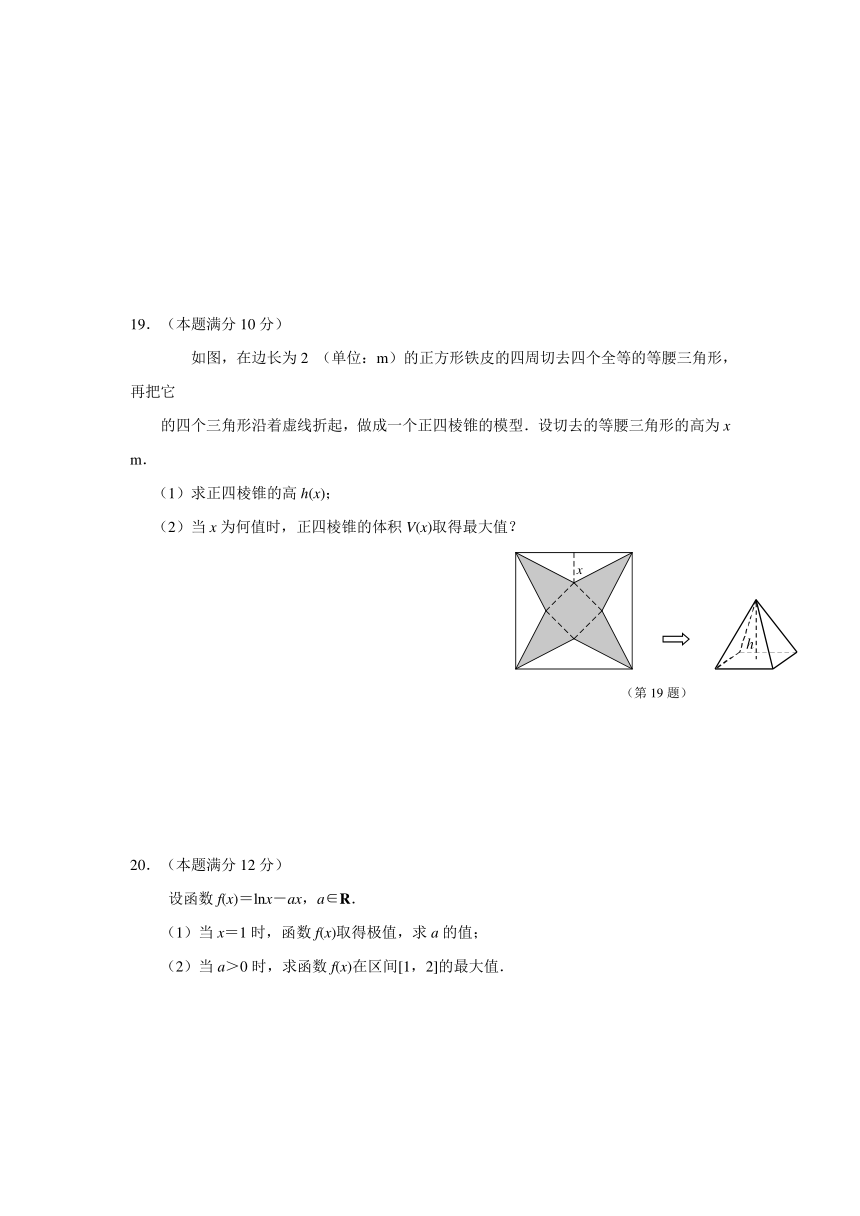
如图,在边长为2 (单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它
的四个三角形沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.
(1)求正四棱锥的高h(x);
(2)当x为何值时,正四棱锥的体积V(x)取得最大值?
20.(本题满分12分)
设函数f(x)=lnx-ax,a∈R.
(1)当x=1时,函数f(x)取得极值,求a的值;
(2)当a>0时,求函数f(x)在区间[1,2]的最大值.
2012-2013学年度第一学期期末调研测试卷
高二数学(文)参考答案及评分标准 2013.01
说明:
1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,填空题不给中间分数.
一、填空题(本大题共14小题,每小题3分,共42分)
1.四. 2.(x∈R,x2≤x-1. 3.x2=-16y. 4.5.
5.3x±y=0. 6.充分不必要. 7.-2. 8.1.
9.(0,2).开闭区间均可 10.2. 11.(-)×. 12.5.
13. . 14.1.
说明:填空题的严格按照评分标准,没有中间分,第5题少解或有错解不得分.
二、解答题(本大题共6小题,共58分.解答应写出文字说明、证明过程或演算步骤)
15.(本题满分8分)
解 (1)因为z1·i=1+i,
所以z1==1-i. ………………………………4分
(2)因为z2的虚部为2,故设z2=m+2i (m∈R).
因为z1·z2=(1-i)(m+2i)=(m+2)+(2-m)i为纯虚数, ………………………………6分
所以m+2=0,且2-m≠0,解得m=-2.
所以z2=-2+2i. ………………………………8分
说明:按评分标准给分.第(1)问也可用待定系数求,列出方程给2分,得出结果给2分,第(2)问中不说明2-m≠0不扣分.
16.(本题满分8分)
解(1)记f(x)=x2+1,x∈R,则f(x)的最小值为1, ………………………………2分
因为命题p为真命题,所以a≤f(x)min=1,
即a的取值范围为(-∞,1]. ………………………………4分
(2)因为q为真命题,所以a+2>0,解得a>-2. ………………………………6分
因为“p且q”为真命题,所以即a的取值范围为(-2,1].
………………………………8分
说明:第(1)问得出命题p为真命题的等价条件a≤1,给4分,没过程不扣分,
第(2)问分两步给,得到a>-2给2分,得到x∈(-2,1]给2分,少一步扣2分.
17.(本题满分10分)
解 (1)因为直线AB的斜率k=1,AB中点坐标为M(2,5), ……………………2分
所以直线CD方程为y-5=-(x-2),即x+y-7=0. ……………………………4分
(2)设圆心P(a,b),则由P在CD上得,
a+b-7=0. ①
又直径CD=4,所以PA=2,即(a-1)2+(b-4)2=4. ② …………………………6分
由①②解得或
所以圆心P(1,6)或P(3,4).
所以圆P的方程为(x-1)2+(y-6)2=4或(x-3)2+(y-4)2=4. ………………………10分
说明:按评分标准给分,第(2)问若少一解扣2分.
18.(本题满分10分)
解 (1)因为B在右准线上,且F恰好为线段AB的中点,
所以2c=, ………………………………2分
即=,所以椭圆的离心率e=. ………………………………4分
(2)由(1)知a=c,b=c,所以直线AB的方程为y=x-c,即x-y-c=0, ……6分
因为直线AB与圆x2+y2=2相切,所以=, ………………………………8分
解得c=2.所以a=2,b=2.
所以椭圆C的方程为+=1. ………………………………10分
说明:按评分标准给分.
19.(本题满分10分)
解 (1)设正四棱锥的底面中心为O,一侧棱为AN.
由于切去的是等腰三角形,所以AN=,NO=1-x,
………………………………2分
在直角三角形AON中,AO===,
因此h(x)=,(0<x<1). ………………………………4分
(不写0<x<1扣1分)
(2)V(x)=··[2(1-x)]2·=(1-x)2,(0<x<1). ………………………6分
由V ′(x)=[(2x-2)+]=(x-1)=0, ………………………8分
解得x=1(舍去),x=.
当x∈(0,)时,V ′(x)>0,V(x)为增函数;当x∈(,1)时,V ′(x)<0,V(x)为减函数.
所以函数V(x)在x=时取得极大值,也为V(x)的最大值.
答:当x为m时,正四棱锥的体积V(x)取得最大值. ………………………………10分
说明:按评分标准给分,不写函数的定义域扣1分,没有答扣1分.
20.(本题满分12分)
解 (1)f(x)的定义域为(0,+∞),
所以f ′(x)=-a=. ………………………………2分
因为当x=1时,函数f(x)取得极值,
所以f ′(1)=1-a=0,所以a=1.
经检验,a=1符合题意.(不检验不扣分) ………………………………4分
(2)f ′(x)=-a=,x>0.
令f ′(x)=0得x=.因为x∈(0,)时,f ′(x)>0,x∈(,+∞)时,f ′(x)<0,
所以f(x)在(0,)递增,在(,+∞)递减, ………………………………6分
①当0<≤1,即a≥1时,f(x)在(1,2)上递减,所以x=1时,f(x)取最大值f(1)=-a;
………………………………8分
②当1<<2,即<a<1时,f(x)在(1,)上递增,在( ,2)上递减,
所以x=时,f(x)取最大值f()=-lna-1; ………………………………10分
③当≥2,即0<a≤时,f(x)在(1,2)上递增,所以x=2时,f(x)取最大值f(2)=ln2-2a;
综上,①当0<a≤时,f(x)最大值为ln2-2a;②当<a<1时,f(x)最大值为-lna-1.
③当a≥1时,f(x)最大值为-a. ………………………………12分
说明:第(1)问,不检验不扣分;第(2)问的讨论,每一种情形给2分;不总结结论不扣分.
高二数学试卷(文科) 2013.01
注意事项:
1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为100分,考试时间为100分钟.
2.答题前,请务必将自己的姓名、学校、班级、学号写在答卷纸的密封线内.试题的答案写在答卷纸上对应题目的答案空格内.考试结束后,交回答卷纸.
参考公式:V锥体=Sh (S表示底面面积,h表示锥体的高).
一、填空题:本大题共14小题,每小题3分,共42分.请把答案填写在答卷纸相应位置上
1.复数1-2i (i为虚数单位)在复平面内对应的点位于第 ▲ 象限.
2.已知命题p:(x∈R,x2>x-1,则(p为 ▲ .
3.在平面直角坐标系中,准线方程为y=4的抛物线标准的方程为 ▲ .
4.若复数z=4+3i (i为虚数单位),则|z |= ▲ .
5.双曲线x2-=1的渐近线方程为 ▲ .
6.“x>1”是“x>0”成立的 ▲ 条件(在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选出一种).
7.已知曲线y=ax2在x=1处切线的斜率是-4,则实数a的值为 ▲ .
8.若圆x2+y2=4与圆x2+(y-3)2=r2 (r>0)外切,则实数r的值为 ▲ .
9.函数y=x3-3x2+1的单调递减区间为 ▲ .
10.若直线3x+4y-12=0与圆(x-3)2+(y-2)2=4相交于M,N两点,则线段MN的长为 ▲ ..
11.观察下列等式:
=(-)×,
=(-)×,
=(-)×,
=(-)×,
………………
可推测当n≥3,n∈N*时,= ▲ .
12.已知椭圆+=1与双曲线—y2=1有共同焦点F1,F2,点P是两曲线的一个交点,
则PF1·PF2= ▲ .
13.在直角三角形ABC中,∠C为直角,两直角边长分别为a,b,求其外接圆半径时,可采取如下方法:将三角形ABC补成以其两直角边为邻边的矩形,则矩形的对角线为三角形外接圆的直径,可得三角形外接圆半径为;按此方法,在三棱锥S-ABC中,三条侧棱两两互相垂直,且长度分别为a,b,c,通过类比可得三棱锥S-ABC外接球的半径为 ▲ .
14.若函数f(x)在定义域D内某区间I上是增函数,且在I上是减函数,则称y=f(x)在I 上是“弱
增函数”.已知函数h(x)=x2-(b-1)x+b在(0,1]上是“弱增函数”,则实数b的值为 ▲ .
二、解答题:本大题共6小题,共计58分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本题满分8分)
已知复数z1满足z1·i=1+i (i为虚数单位),复数z2的虚部为2.
(1)求z1;
(2)若z1·z2是纯虚数,求z2.
16.(本题满分8分)
已知命题p:任意x∈R,x2+1≥a,命题q:方程-=1表示双曲线.
(1)若命题p为真命题,求实数a的取值范围;
(2)若 “p且q”为真命题,求实数a的取值范围.
17.(本题满分10分)
已知以点P为圆心的圆经过点A(1,4),B(3,6),线段AB的垂直平分线与圆P交于点
C,D,且CD=4.
(1)求直线CD的方程;
(2)求圆P的方程.
18.(本题满分10分)
如图,已知椭圆C:+=1(a>b>0)的右焦点为F(c,0),下顶点为A(0,-b),直线AF
与椭圆的右准线交于点B,若F恰好为线段AB的中点.
(1)求椭圆C的离心率;
(2)若直线AB与圆x2+y2=2相切,求椭圆C的方程.
19.(本题满分10分)
如图,在边长为2 (单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它
的四个三角形沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.
(1)求正四棱锥的高h(x);
(2)当x为何值时,正四棱锥的体积V(x)取得最大值?
20.(本题满分12分)
设函数f(x)=lnx-ax,a∈R.
(1)当x=1时,函数f(x)取得极值,求a的值;
(2)当a>0时,求函数f(x)在区间[1,2]的最大值.
2012-2013学年度第一学期期末调研测试卷
高二数学(文)参考答案及评分标准 2013.01
说明:
1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,填空题不给中间分数.
一、填空题(本大题共14小题,每小题3分,共42分)
1.四. 2.(x∈R,x2≤x-1. 3.x2=-16y. 4.5.
5.3x±y=0. 6.充分不必要. 7.-2. 8.1.
9.(0,2).开闭区间均可 10.2. 11.(-)×. 12.5.
13. . 14.1.
说明:填空题的严格按照评分标准,没有中间分,第5题少解或有错解不得分.
二、解答题(本大题共6小题,共58分.解答应写出文字说明、证明过程或演算步骤)
15.(本题满分8分)
解 (1)因为z1·i=1+i,
所以z1==1-i. ………………………………4分
(2)因为z2的虚部为2,故设z2=m+2i (m∈R).
因为z1·z2=(1-i)(m+2i)=(m+2)+(2-m)i为纯虚数, ………………………………6分
所以m+2=0,且2-m≠0,解得m=-2.
所以z2=-2+2i. ………………………………8分
说明:按评分标准给分.第(1)问也可用待定系数求,列出方程给2分,得出结果给2分,第(2)问中不说明2-m≠0不扣分.
16.(本题满分8分)
解(1)记f(x)=x2+1,x∈R,则f(x)的最小值为1, ………………………………2分
因为命题p为真命题,所以a≤f(x)min=1,
即a的取值范围为(-∞,1]. ………………………………4分
(2)因为q为真命题,所以a+2>0,解得a>-2. ………………………………6分
因为“p且q”为真命题,所以即a的取值范围为(-2,1].
………………………………8分
说明:第(1)问得出命题p为真命题的等价条件a≤1,给4分,没过程不扣分,
第(2)问分两步给,得到a>-2给2分,得到x∈(-2,1]给2分,少一步扣2分.
17.(本题满分10分)
解 (1)因为直线AB的斜率k=1,AB中点坐标为M(2,5), ……………………2分
所以直线CD方程为y-5=-(x-2),即x+y-7=0. ……………………………4分
(2)设圆心P(a,b),则由P在CD上得,
a+b-7=0. ①
又直径CD=4,所以PA=2,即(a-1)2+(b-4)2=4. ② …………………………6分
由①②解得或
所以圆心P(1,6)或P(3,4).
所以圆P的方程为(x-1)2+(y-6)2=4或(x-3)2+(y-4)2=4. ………………………10分
说明:按评分标准给分,第(2)问若少一解扣2分.
18.(本题满分10分)
解 (1)因为B在右准线上,且F恰好为线段AB的中点,
所以2c=, ………………………………2分
即=,所以椭圆的离心率e=. ………………………………4分
(2)由(1)知a=c,b=c,所以直线AB的方程为y=x-c,即x-y-c=0, ……6分
因为直线AB与圆x2+y2=2相切,所以=, ………………………………8分
解得c=2.所以a=2,b=2.
所以椭圆C的方程为+=1. ………………………………10分
说明:按评分标准给分.
19.(本题满分10分)
解 (1)设正四棱锥的底面中心为O,一侧棱为AN.
由于切去的是等腰三角形,所以AN=,NO=1-x,
………………………………2分
在直角三角形AON中,AO===,
因此h(x)=,(0<x<1). ………………………………4分
(不写0<x<1扣1分)
(2)V(x)=··[2(1-x)]2·=(1-x)2,(0<x<1). ………………………6分
由V ′(x)=[(2x-2)+]=(x-1)=0, ………………………8分
解得x=1(舍去),x=.
当x∈(0,)时,V ′(x)>0,V(x)为增函数;当x∈(,1)时,V ′(x)<0,V(x)为减函数.
所以函数V(x)在x=时取得极大值,也为V(x)的最大值.
答:当x为m时,正四棱锥的体积V(x)取得最大值. ………………………………10分
说明:按评分标准给分,不写函数的定义域扣1分,没有答扣1分.
20.(本题满分12分)
解 (1)f(x)的定义域为(0,+∞),
所以f ′(x)=-a=. ………………………………2分
因为当x=1时,函数f(x)取得极值,
所以f ′(1)=1-a=0,所以a=1.
经检验,a=1符合题意.(不检验不扣分) ………………………………4分
(2)f ′(x)=-a=,x>0.
令f ′(x)=0得x=.因为x∈(0,)时,f ′(x)>0,x∈(,+∞)时,f ′(x)<0,
所以f(x)在(0,)递增,在(,+∞)递减, ………………………………6分
①当0<≤1,即a≥1时,f(x)在(1,2)上递减,所以x=1时,f(x)取最大值f(1)=-a;
………………………………8分
②当1<<2,即<a<1时,f(x)在(1,)上递增,在( ,2)上递减,
所以x=时,f(x)取最大值f()=-lna-1; ………………………………10分
③当≥2,即0<a≤时,f(x)在(1,2)上递增,所以x=2时,f(x)取最大值f(2)=ln2-2a;
综上,①当0<a≤时,f(x)最大值为ln2-2a;②当<a<1时,f(x)最大值为-lna-1.
③当a≥1时,f(x)最大值为-a. ………………………………12分
说明:第(1)问,不检验不扣分;第(2)问的讨论,每一种情形给2分;不总结结论不扣分.
同课章节目录
