平行线性质与判定综合训练题
文档属性
| 名称 | 平行线性质与判定综合训练题 |  | |
| 格式 | zip | ||
| 文件大小 | 160.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-02 21:48:22 | ||
图片预览

文档简介
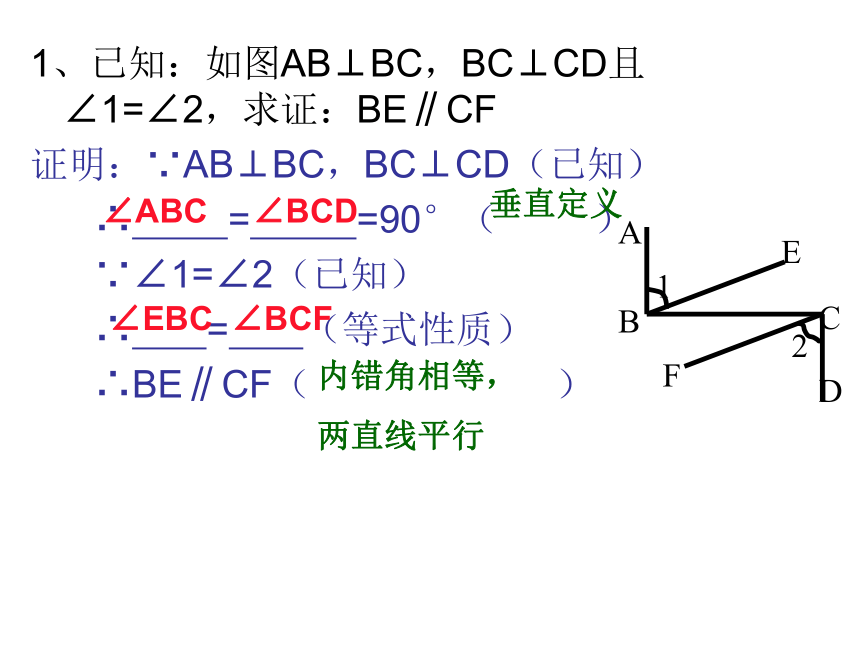
课件17张PPT。平行线1、已知:如图AB⊥BC,BC⊥CD且∠1=∠2,求证:BE∥CF
证明:∵AB⊥BC,BC⊥CD(已知)
∴ = =90°( )
∵∠1=∠2(已知)
∴ = (等式性质)
∴BE∥CF( )∠ABC∠BCD垂直定义∠EBC∠BCF内错角相等,
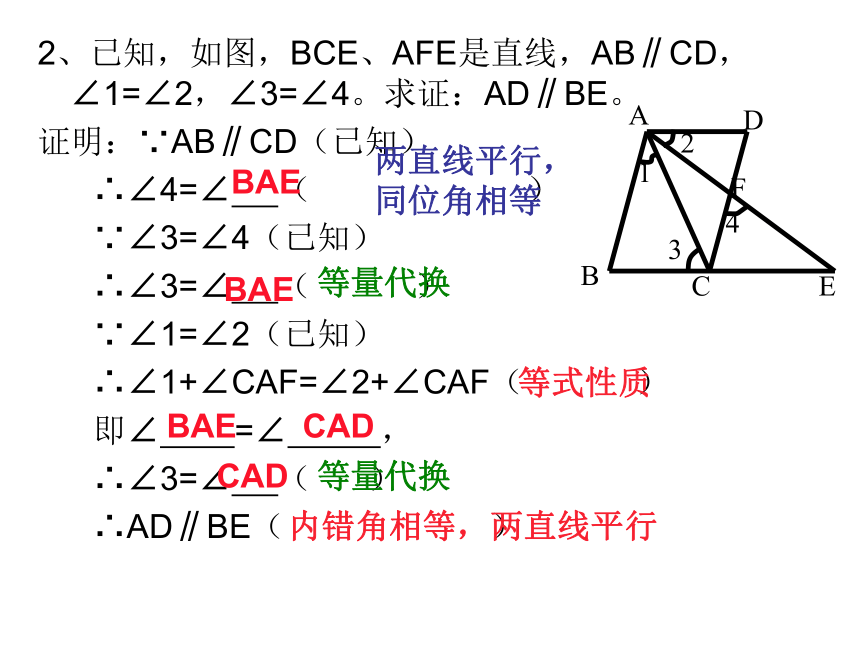
两直线平行2、已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4。求证:AD∥BE。
证明:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF( )
即∠ =∠ ,
∴∠3=∠ ( )
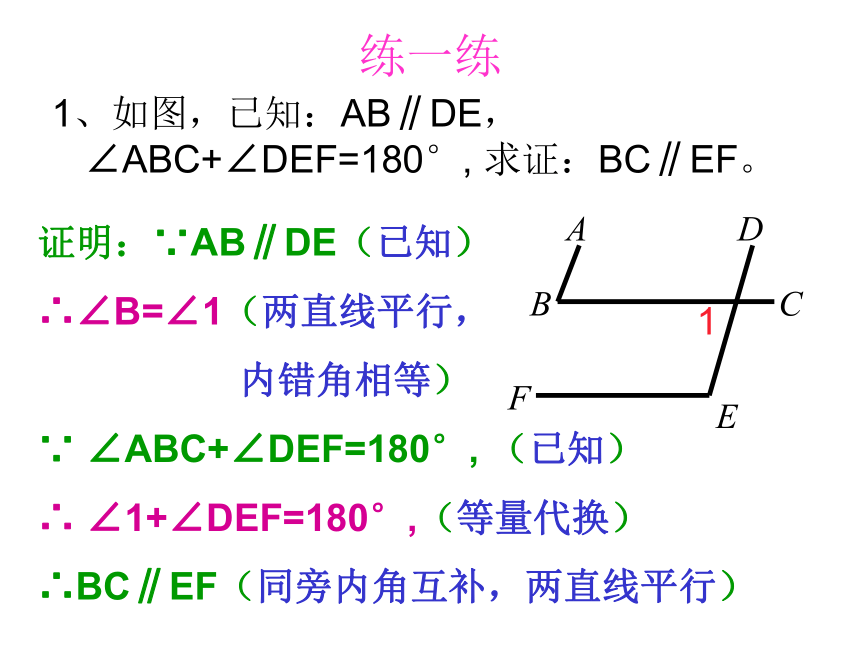
∴AD∥BE( )BAE两直线平行,同位角相等BAE等量代换等式性质BAECADCAD等量代换内错角相等,两直线平行练一练 1、如图,已知:AB∥DE,∠ABC+∠DEF=180°, 求证:BC∥EF。 证明:∵AB∥DE(已知)
∴∠B=∠1(两直线平行,
内错角相等)
∵ ∠ABC+∠DEF=180°, (已知)
∴ ∠1+∠DEF=180°,(等量代换)
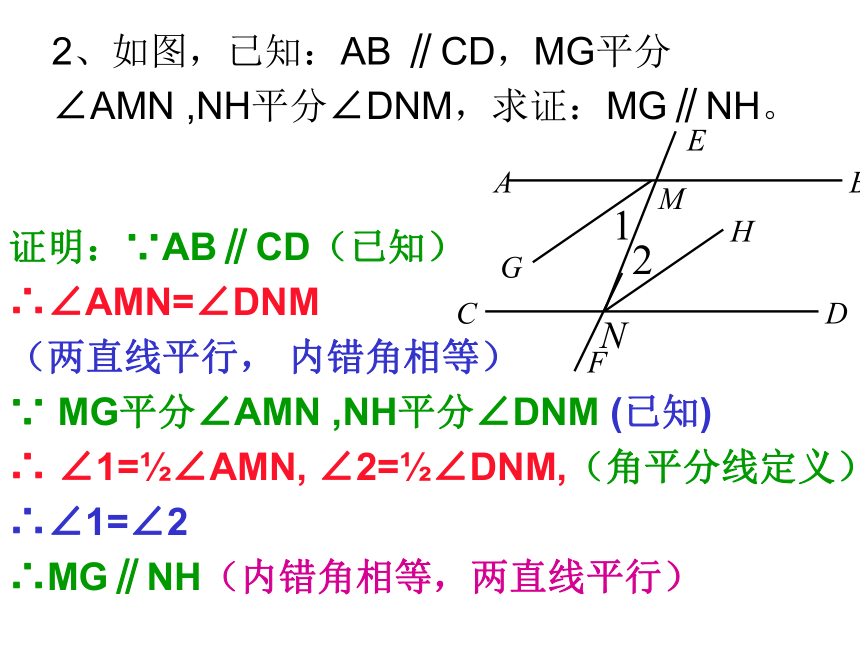
∴BC∥EF(同旁内角互补,两直线平行)12、如图,已知:AB ∥CD,MG平分∠AMN ,NH平分∠DNM,求证:MG∥NH。 证明:∵AB∥CD(已知)
∴∠AMN=∠DNM
(两直线平行, 内错角相等)
∵ MG平分∠AMN ,NH平分∠DNM (已知)
∴ ∠1=?∠AMN, ∠2=?∠DNM,(角平分线定义)
∴∠1=∠2
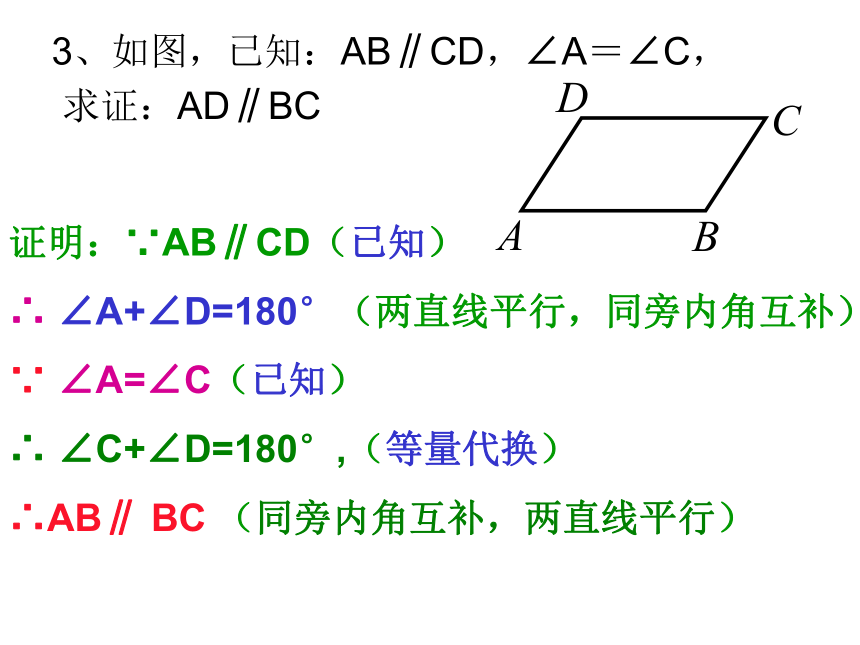
∴MG∥NH(内错角相等,两直线平行)3、如图,已知:AB∥CD,∠A=∠C, 求证:AD∥BC 证明:∵AB∥CD(已知)
∴ ∠A+∠D=180°(两直线平行,同旁内角互补)
∵ ∠A=∠C(已知)
∴ ∠C+∠D=180°,(等量代换)
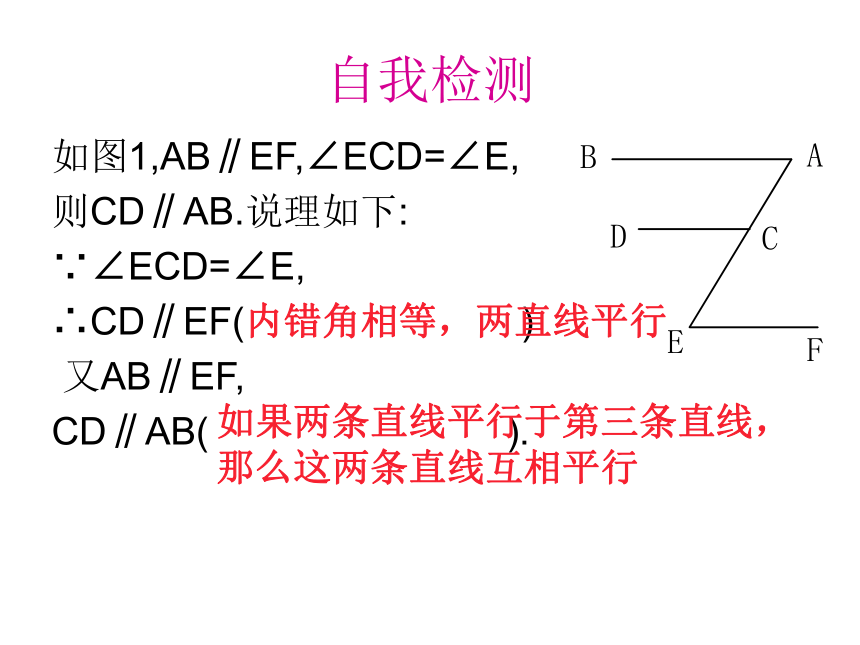
∴AB∥ BC (同旁内角互补,两直线平行)自我检测如图1,AB∥EF,∠ECD=∠E,
则CD∥AB.说理如下:
∵∠ECD=∠E,
∴CD∥EF( )
又AB∥EF,
CD∥AB( ). 内错角相等,两直线平行如果两条直线平行于第三条直线,那么这两条直线互相平行2、下列说法:
①两条直线平行,同旁内角互补;
②同位角相等,两直线平行;
③内错角相等,两直线平行;
④垂直于同一直线的两直线平行,
其中是平行线的性质的是( )
A.① B.②和③ C.④ D.①和④A如图,平行光线AB、DE照射在平面镜上,经反射得到光线BC与EF,已知∠1= ∠2, ∠3= ∠4,则光线BC与EF平行吗?为什么?证明:∵AB∥ED(已知)
∴ ∠1=∠3(两直线平行,同位角相等)
∵ ∠1=∠2, ∠3=∠4 (已知)
∴ ∠2=∠4,(等量代换)
∴BC∥ EF(同位角相等,两直线平行)4、如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D. (1)∠ABD与∠C相等吗?为什么. (2)∠A与∠F相等吗?请说明理由.1)证明:∵ ∠1=∠2(已知)
∴ BD∥CE(内错角相等,
两直线平行)
∴ ∠ABD=∠C(两直线平行,
同位角相等)2)证明:由1)可知, ∠ABD=∠C
∵∠C=∠D(已知) ∴∠ABD=∠D(等量代换)
∴ DF∥AC(内错角相等,两直线平行)
∴ ∠A=∠F,(两直线平行,内错角相等)5、如图,已知EAB是直线,AD∥BC,AD平分∠EAC,试判定∠B与∠C的大小关系,并说明理由.解: ∠B=∠C,理由如下:
∵AD∥BC(已知)
∴ ∠DAC=∠C(两直线平行,
内错角相等)
∠DAE=∠B(两直线平行,
同位角相等)
∵ AD平分∠EAC ,
∴ ∠EAD=∠DAC(角平分线定义)
∴∠B=∠C(等量代换)1.已知,如图1,∠AOB纸片沿CD折叠,若O′C∥BD,那么O′D与AC平行吗?请说明理由.解: O′D ∥AC,理由如下:
由折叠可知,∠1=∠2, ∠3=∠4
∵O′C∥BD, (已知)
∴∠2=∠3(两直线平行,内错角相等)
∴ ∠1=∠4,(等量代换)
∴ O′D ∥AC(内错角相等,两直线平行)2、如图,EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。证明:∵AB⊥DC,AB⊥EF(已知)
∴∠BDC=∠BEF=90°(垂直定义)
∴EF∥CD(同位角相等,两直线平行) ∴∠EFB=∠DCB(两直线平行,同位角相等)
∵ ∠EFB=∠GDC
∴∠DCB=∠GDC (等量代换)
∴ DG∥BC(内错角相等,两直线平行) ∴∠AGD=∠ACB(两直线平行,同位角相等)
证明:∵AB⊥BC,BC⊥CD(已知)
∴ = =90°( )
∵∠1=∠2(已知)
∴ = (等式性质)
∴BE∥CF( )∠ABC∠BCD垂直定义∠EBC∠BCF内错角相等,
两直线平行2、已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4。求证:AD∥BE。
证明:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF( )
即∠ =∠ ,
∴∠3=∠ ( )
∴AD∥BE( )BAE两直线平行,同位角相等BAE等量代换等式性质BAECADCAD等量代换内错角相等,两直线平行练一练 1、如图,已知:AB∥DE,∠ABC+∠DEF=180°, 求证:BC∥EF。 证明:∵AB∥DE(已知)
∴∠B=∠1(两直线平行,
内错角相等)
∵ ∠ABC+∠DEF=180°, (已知)
∴ ∠1+∠DEF=180°,(等量代换)
∴BC∥EF(同旁内角互补,两直线平行)12、如图,已知:AB ∥CD,MG平分∠AMN ,NH平分∠DNM,求证:MG∥NH。 证明:∵AB∥CD(已知)
∴∠AMN=∠DNM
(两直线平行, 内错角相等)
∵ MG平分∠AMN ,NH平分∠DNM (已知)
∴ ∠1=?∠AMN, ∠2=?∠DNM,(角平分线定义)
∴∠1=∠2
∴MG∥NH(内错角相等,两直线平行)3、如图,已知:AB∥CD,∠A=∠C, 求证:AD∥BC 证明:∵AB∥CD(已知)
∴ ∠A+∠D=180°(两直线平行,同旁内角互补)
∵ ∠A=∠C(已知)
∴ ∠C+∠D=180°,(等量代换)
∴AB∥ BC (同旁内角互补,两直线平行)自我检测如图1,AB∥EF,∠ECD=∠E,
则CD∥AB.说理如下:
∵∠ECD=∠E,
∴CD∥EF( )
又AB∥EF,
CD∥AB( ). 内错角相等,两直线平行如果两条直线平行于第三条直线,那么这两条直线互相平行2、下列说法:
①两条直线平行,同旁内角互补;
②同位角相等,两直线平行;
③内错角相等,两直线平行;
④垂直于同一直线的两直线平行,
其中是平行线的性质的是( )
A.① B.②和③ C.④ D.①和④A如图,平行光线AB、DE照射在平面镜上,经反射得到光线BC与EF,已知∠1= ∠2, ∠3= ∠4,则光线BC与EF平行吗?为什么?证明:∵AB∥ED(已知)
∴ ∠1=∠3(两直线平行,同位角相等)
∵ ∠1=∠2, ∠3=∠4 (已知)
∴ ∠2=∠4,(等量代换)
∴BC∥ EF(同位角相等,两直线平行)4、如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D. (1)∠ABD与∠C相等吗?为什么. (2)∠A与∠F相等吗?请说明理由.1)证明:∵ ∠1=∠2(已知)
∴ BD∥CE(内错角相等,
两直线平行)
∴ ∠ABD=∠C(两直线平行,
同位角相等)2)证明:由1)可知, ∠ABD=∠C
∵∠C=∠D(已知) ∴∠ABD=∠D(等量代换)
∴ DF∥AC(内错角相等,两直线平行)
∴ ∠A=∠F,(两直线平行,内错角相等)5、如图,已知EAB是直线,AD∥BC,AD平分∠EAC,试判定∠B与∠C的大小关系,并说明理由.解: ∠B=∠C,理由如下:
∵AD∥BC(已知)
∴ ∠DAC=∠C(两直线平行,
内错角相等)
∠DAE=∠B(两直线平行,
同位角相等)
∵ AD平分∠EAC ,
∴ ∠EAD=∠DAC(角平分线定义)
∴∠B=∠C(等量代换)1.已知,如图1,∠AOB纸片沿CD折叠,若O′C∥BD,那么O′D与AC平行吗?请说明理由.解: O′D ∥AC,理由如下:
由折叠可知,∠1=∠2, ∠3=∠4
∵O′C∥BD, (已知)
∴∠2=∠3(两直线平行,内错角相等)
∴ ∠1=∠4,(等量代换)
∴ O′D ∥AC(内错角相等,两直线平行)2、如图,EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。证明:∵AB⊥DC,AB⊥EF(已知)
∴∠BDC=∠BEF=90°(垂直定义)
∴EF∥CD(同位角相等,两直线平行) ∴∠EFB=∠DCB(两直线平行,同位角相等)
∵ ∠EFB=∠GDC
∴∠DCB=∠GDC (等量代换)
∴ DG∥BC(内错角相等,两直线平行) ∴∠AGD=∠ACB(两直线平行,同位角相等)
