人教版数学八年级下册第二十章 数据的分析20.1.1平均数(第一课时) 课件(共16张PPT)
文档属性
| 名称 | 人教版数学八年级下册第二十章 数据的分析20.1.1平均数(第一课时) 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 649.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-09 18:09:34 | ||
图片预览




文档简介
(共16张PPT)
新人教版初中数学八年级(下) 平均数
新人教版初中数学八年级(下) 平均数
一般地,对于n个数x1,x2,…,xn,我们把
叫做这n个数的算术平均数。
请计算下列各数的平均数: 35 20 75 68 52
问题1 在一次数学考试中,某班级有5名同学得120分,有35名同学得70分,
120×5 +70×35
5+35
=76.25
权
新课讲解:
(1)那么这个班级的数学平均分是(120+70)÷2=95分
(2)这个平均分会趋近120呢?还是70 呢?为什么?
加权平均数
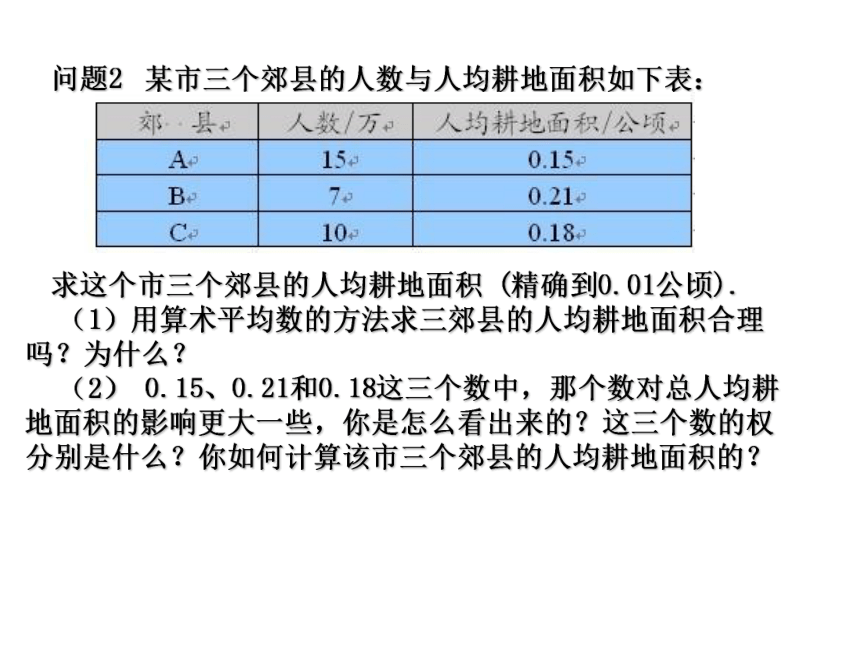
问题2 某市三个郊县的人数与人均耕地面积如下表:
求这个市三个郊县的人均耕地面积 (精确到0.01公顷).
(1)用算术平均数的方法求三郊县的人均耕地面积合理吗?为什么?
(2) 0.15、0.21和0.18这三个数中,那个数对总人均耕地面积的影响更大一些,你是怎么看出来的?这三个数的权分别是什么?你如何计算该市三个郊县的人均耕地面积的?
一般地,若n个数 的权分别是 ,我们把
叫做这n个数的加权平均数.
权(weight)表示数据重要程度
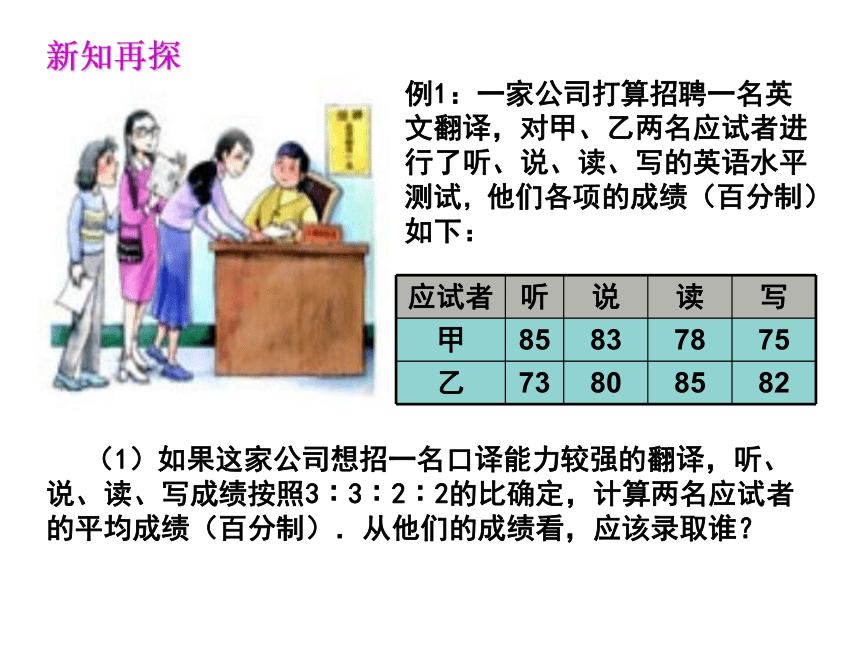
例1:一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(1)如果这家公司想招一名口译能力较强的翻译,听、说、读、写成绩按照3∶3∶2∶2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
新知再探
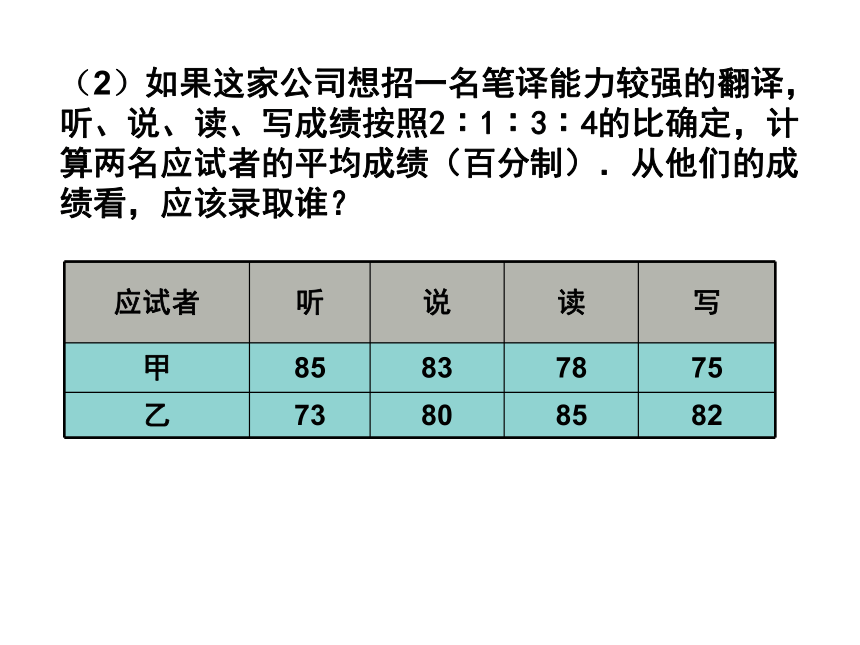
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2∶1∶3∶4的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(2)解:听、说、读、写的成绩按照2∶1∶3∶4的比确定,则甲的平均成绩为
85×2+83×1+78×3+75×4
2+1+3+4
=
78.7
乙的平均成绩为
73×2+80×1+85×3+82×4
2+1+3+4
=
80.9
因为乙的成绩比甲的高,所以从成绩看,应该录取乙.
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(3)①如果这家公司想招一名综合能力较强的翻译,听、说、读、写成绩的权分别是多少?
②计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
85×1+83×1+78×1+75×1
1+1+1+1
=85×1+83×1+78×1+75×1
4
=80.25
73×1+80×1+85×1+82×1
1+1+1+1
=73×1+80×1+85×1+82×1
4
=80
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
从成绩看,应该录取甲。
例2:一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,计算选手的综合成绩(百分制)。进入决赛的前两名选手的单项成绩如下表所示:
选手 演讲内容 演讲能力 演讲效果
小红 85 95 95
小明 95 85 95
(3)如果想让小红胜出,应该怎么办呢?
(1)若按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,请决出两人的名次。
(2)两名同学都是两个95分和一个85分,为什么最后的得分不同呢?
练习 大润发超市欲招聘一名经理,对甲、乙候选人进行了面试和笔试,他们的成绩如下表所示:
候选人 测试成绩(百分制)
面试 笔试
甲 86 90
乙 92 83
你认为,作为应聘人员应该重视哪方面的成绩?
(1)这节课我们学习的主要内容
(2)这节课我们学习了数学的哪一部分知识?
加权平均数的意义
数据的权的意义
加权平均数与算术平均数的联系
加权平均数公式
权的三种表现形式
作业:
1、必做题:教科书P121页第1题、
第2题(只计算平均数)
2、选做题:教科书P122页第5题
课后任务
练习2:晨光中学规定学生的学期体育成绩满分为100分,其中早操占20%,期中考试成绩占30%,期末考试成绩占50%.小红同学的三项成绩(百分制)依次为95分、90分、85分,小红这学期的体育成绩是多少?
解:小红这学期的体育成绩是
95×20%+90×30%+85×50%
20%+30%+50%
=19+27+42.5
=88.5.
练习3: 某校八年级一班有学生50人,八年级二班有学生45人,八年级三班55人,期末数学测试中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,三班的平均分76.4分,这三个班的平均分是多少?
解:(81.5×50 +83.4×45+76.4×55)
50+45+55
=80.2
答:这三个班的数学平均分是80.2分.
新人教版初中数学八年级(下) 平均数
新人教版初中数学八年级(下) 平均数
一般地,对于n个数x1,x2,…,xn,我们把
叫做这n个数的算术平均数。
请计算下列各数的平均数: 35 20 75 68 52
问题1 在一次数学考试中,某班级有5名同学得120分,有35名同学得70分,
120×5 +70×35
5+35
=76.25
权
新课讲解:
(1)那么这个班级的数学平均分是(120+70)÷2=95分
(2)这个平均分会趋近120呢?还是70 呢?为什么?
加权平均数
问题2 某市三个郊县的人数与人均耕地面积如下表:
求这个市三个郊县的人均耕地面积 (精确到0.01公顷).
(1)用算术平均数的方法求三郊县的人均耕地面积合理吗?为什么?
(2) 0.15、0.21和0.18这三个数中,那个数对总人均耕地面积的影响更大一些,你是怎么看出来的?这三个数的权分别是什么?你如何计算该市三个郊县的人均耕地面积的?
一般地,若n个数 的权分别是 ,我们把
叫做这n个数的加权平均数.
权(weight)表示数据重要程度
例1:一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(1)如果这家公司想招一名口译能力较强的翻译,听、说、读、写成绩按照3∶3∶2∶2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
新知再探
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2∶1∶3∶4的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(2)解:听、说、读、写的成绩按照2∶1∶3∶4的比确定,则甲的平均成绩为
85×2+83×1+78×3+75×4
2+1+3+4
=
78.7
乙的平均成绩为
73×2+80×1+85×3+82×4
2+1+3+4
=
80.9
因为乙的成绩比甲的高,所以从成绩看,应该录取乙.
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(3)①如果这家公司想招一名综合能力较强的翻译,听、说、读、写成绩的权分别是多少?
②计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
85×1+83×1+78×1+75×1
1+1+1+1
=85×1+83×1+78×1+75×1
4
=80.25
73×1+80×1+85×1+82×1
1+1+1+1
=73×1+80×1+85×1+82×1
4
=80
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
从成绩看,应该录取甲。
例2:一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,计算选手的综合成绩(百分制)。进入决赛的前两名选手的单项成绩如下表所示:
选手 演讲内容 演讲能力 演讲效果
小红 85 95 95
小明 95 85 95
(3)如果想让小红胜出,应该怎么办呢?
(1)若按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,请决出两人的名次。
(2)两名同学都是两个95分和一个85分,为什么最后的得分不同呢?
练习 大润发超市欲招聘一名经理,对甲、乙候选人进行了面试和笔试,他们的成绩如下表所示:
候选人 测试成绩(百分制)
面试 笔试
甲 86 90
乙 92 83
你认为,作为应聘人员应该重视哪方面的成绩?
(1)这节课我们学习的主要内容
(2)这节课我们学习了数学的哪一部分知识?
加权平均数的意义
数据的权的意义
加权平均数与算术平均数的联系
加权平均数公式
权的三种表现形式
作业:
1、必做题:教科书P121页第1题、
第2题(只计算平均数)
2、选做题:教科书P122页第5题
课后任务
练习2:晨光中学规定学生的学期体育成绩满分为100分,其中早操占20%,期中考试成绩占30%,期末考试成绩占50%.小红同学的三项成绩(百分制)依次为95分、90分、85分,小红这学期的体育成绩是多少?
解:小红这学期的体育成绩是
95×20%+90×30%+85×50%
20%+30%+50%
=19+27+42.5
=88.5.
练习3: 某校八年级一班有学生50人,八年级二班有学生45人,八年级三班55人,期末数学测试中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,三班的平均分76.4分,这三个班的平均分是多少?
解:(81.5×50 +83.4×45+76.4×55)
50+45+55
=80.2
答:这三个班的数学平均分是80.2分.
