人教版八年级下册 18.2.1矩形及其性质 同步练习(word版含答案)
文档属性
| 名称 | 人教版八年级下册 18.2.1矩形及其性质 同步练习(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 100.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 09:40:33 | ||
图片预览


文档简介
18.2.1 矩形
第1课时 矩形及其性质
A 基础题夯实
核心知识点1 矩形的性质
1.在矩形ABCD中,AC,BD相交于点O,下列说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=AB D.OA=OB
2.矩形的对角线长为10,两邻边之比为3:4,则矩形的周长为 .
3.在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=4 cm,则AC的长为 cm.
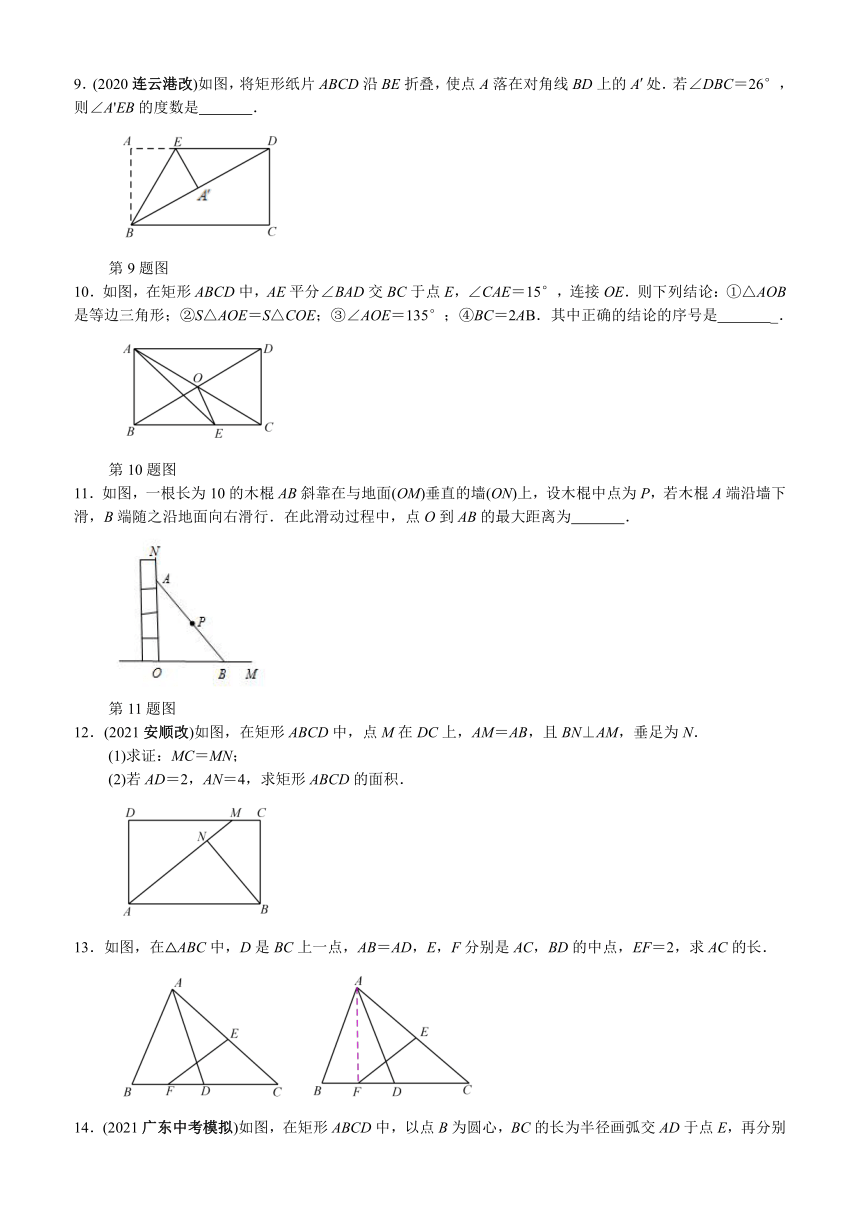
4.(2019福建)如图,点E,F分别是矩形ABCD的边AB,CD上的一点,且DF=BE.求证:AF=CE.
5.(2020毕节改)如图,在矩形ABCD中,AC,BD相交于点O,E,F分别是AO,AD的中点,连接EF,若AB=9 cm,BC=12 cm.求EF的长.
核心知识点2 直角三角形斜边上的中线
6.在Rt△ABC中,∠ACB=90°,D是AB的中点,AC=4,BC=6,则CD的长为 .
7.(2021华师一附中)如图,在口ABCD中,对角线AC,BD交于点E,AC⊥BC,点F是BE的中点,连接CF.若BC=4,CF=2.5,求AB的长.
8.【教材变式】(P61-9改)如图,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是AB的中点.
(1)求∠A的度数;
(2)求证:AE=DE.
B 中档题运用
9.(2020连云港改)如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的处.若∠DBC=26°,则∠A'EB的度数是 .
第9题图
10.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE.则下列结论:①△AOB是等边三角形;②S△AOE=S△COE;③∠AOE=135°;④BC=2AB.其中正确的结论的序号是 _.
第10题图
11.如图,一根长为10的木棍AB斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,B端随之沿地面向右滑行.在此滑动过程中,点O到AB的最大距离为 .
第11题图
12.(2021安顺改)如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:MC=MN;
(2)若AD=2,AN=4,求矩形ABCD的面积.
13.如图,在△ABC中,D是BC上一点,AB=AD,E,F分别是AC,BD的中点,EF=2,求AC的长.
14.(2021广东中考模拟)如图,在矩形ABCD中,以点B为圆心,BC的长为半径画弧交AD于点E,再分别以点C,E为圆心,大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G.
(1)求证:∠AEB=2∠FBC;
(2)若AB=6,BC=10.求CG的长.
C 综合题探究
15.(2021眉山改)如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=6,∠DAC=60°,点F在线段AO上,连接DF,以DF为边作等边△DFE,点E和点A分别位于DF两侧.
(1)求证:∠BDE=∠ADF;
(2)求证:EF=EC.
18.2.1 矩形
第1课时 矩形及其性质
A 基础题夯实
核心知识点1 矩形的性质
1.在矩形ABCD中,AC,BD相交于点O,下列说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=AB D.OA=OB
答案:C
2.矩形的对角线长为10,两邻边之比为3:4,则矩形的周长为 .
答案:28
3.在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=4 cm,则AC的长为 cm.
答案:8
4.(2019福建)如图,点E,F分别是矩形ABCD的边AB,CD上的一点,且DF=BE.求证:AF=CE.
证明:法一:∵四边形ABCD是矩形,∴AD=BC,∠D=∠B=90°.
∵DF=BE,∴△ADF≌△CBE,∴AF=CE;
法二:∵四边形ABCD是矩形,∴AB CD,∵DF=BE.∴CFAE,
∴四边形AFCE为平行四边形,∴AF=CE.
5.(2020毕节改)如图,在矩形ABCD中,AC,BD相交于点O,E,F分别是AO,AD的中点,连接EF,若AB=9 cm,BC=12 cm.求EF的长.
解:∵四边形ABCD是矩形,∴∠ABC=90°,BD=AC,B0=OD,∵AB=9 cm,BC=12 cm,∴AC==15(cm),
∴OD=AC=(cm)∵点E,F分别是AO,AD的中点,
∴EF是△AOD的中位线,.∴EF=OD= cm.
核心知识点2 直角三角形斜边上的中线
6.在Rt△ABC中,∠ACB=90°,D是AB的中点,AC=4,BC=6,则CD的长为 .
答案:
7.(2021华师一附中)如图,在口ABCD中,对角线AC,BD交于点E,AC⊥BC,点F是BE的中点,连接CF.若BC=4,CF=2.5,求AB的长.
解:∵AC⊥BC,点F是BE的中点,∴BE=2CF=5,
∴EC===3,
∵四边形ABCD是平行四边形,
∴AC=2EC=6,∴AB===2.
8.【教材变式】(P61-9改)如图,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是AB的中点.
(1)求∠A的度数;
(2)求证:AE=DE.
解:(1)证∠BCD=∠A,∴∠A+3∠A=90°,∴∠A=22.5°;
(2)连接CE,易证CE=AE=BE,∴∠CED=2∠A=45°,∴CE=DE,
∴AE=DE.
B 中档题运用
9.(2020连云港改)如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的处.若∠DBC=26°,则∠A'EB的度数是 .
第9题图
答案:58°
10.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE.则下列结论:①△AOB是等边三角形;②S△AOE=S△COE;③∠AOE=135°;④BC=2AB.其中正确的结论的序号是 _.
第10题图
答案:①②③
11.如图,一根长为10的木棍AB斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,B端随之沿地面向右滑行.在此滑动过程中,点O到AB的最大距离为 .
第11题图
答案:5
12.(2021安顺改)如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:MC=MN;
(2)若AD=2,AN=4,求矩形ABCD的面积.
解:(1)在矩形ABCD中,∠D=90°,DC//AB,∴∠BAN=∠AMD,
∵BN⊥AM,∴∠BNA=90°=∠D,∵AM=AB,∴△ABN≌△MAD(AAS),
∴AN=DM,∵AM=AB=CD,∴MC=MN;
(2)∵BN=AD=2,AN=4,∴AB==2,∴S矩形ABCD=2×2=4.
13.如图,在△ABC中,D是BC上一点,AB=AD,E,F分别是AC,BD的中点,EF=2,求AC的长.
解:连接AF.∵AB=AD,F是BD的中点,∴AF⊥BD.
∵在Rt△ACF中,∠AFC=90°,E是AC的中点,EF=2,∴AC=2EF=4.
14.(2021广东中考模拟)如图,在矩形ABCD中,以点B为圆心,BC的长为半径画弧交AD于点E,再分别以点C,E为圆心,大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G.
(1)求证:∠AEB=2∠FBC;
(2)若AB=6,BC=10.求CG的长.
解:(1)∵四边形ABCD为矩形,∴AD//BC,∴∠AEB=∠EBC.
根据作图过程可知BF是∠EBC的平分线,
∴∠EBC=2∠FBC,∴∠AEB=2∠FBC;
(2)连接EG,∵BE=BC,∠EBG=∠CBG,BG=BG,∴△EBG≌△CBG,.∴设EG=CG=x.
∵四边形ABCD为矩形,∴CD=AB=6,AD=BC=10,∠A=∠D=90°,
∴AE==8,∴ED=AD-AE=2.∵∠D=90°,DG=CD-CG=6-x,
∴ED2+DG2=EG2,∴22+(6-x)2=x2,∴x=.∴CG=.
C 综合题探究
15.(2021眉山改)如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=6,∠DAC=60°,点F在线段AO上,连接DF,以DF为边作等边△DFE,点E和点A分别位于DF两侧.
(1)求证:∠BDE=∠ADF;
(2)求证:EF=EC.
证明:(1)∵四边形ABCD是矩形,∴OA=OB=OC=OD,
∵∠DAC=60°,∴△OAD为等边三角形,
∴∠DOA=∠DAO=∠ODA=60°,AD=OD,
∵△DFE为等边三角形,∴∠EDF=60°,DF=DE=EF,
∵∠BDE+∠FDO=∠ADF+∠FDO=60°,∴∠BDE=∠ADF;
(2)连接OE,由(1)知,AD=OD,∠ADF=∠BDE,DF=DE,∴△ADF≌△ODE,
∴∠DOE=∠DAF=60°.∵∠DOA=60°,∴∠COE=60°=∠DOE.
∵四边形ABCD为矩形,∴AC=BD,OD=BD,OC=AC,∴OD=OC,
∵OE=OE,∴△ODE≌△OCE,∴EC=ED=EF.
第1课时 矩形及其性质
A 基础题夯实
核心知识点1 矩形的性质
1.在矩形ABCD中,AC,BD相交于点O,下列说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=AB D.OA=OB
2.矩形的对角线长为10,两邻边之比为3:4,则矩形的周长为 .
3.在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=4 cm,则AC的长为 cm.
4.(2019福建)如图,点E,F分别是矩形ABCD的边AB,CD上的一点,且DF=BE.求证:AF=CE.
5.(2020毕节改)如图,在矩形ABCD中,AC,BD相交于点O,E,F分别是AO,AD的中点,连接EF,若AB=9 cm,BC=12 cm.求EF的长.
核心知识点2 直角三角形斜边上的中线
6.在Rt△ABC中,∠ACB=90°,D是AB的中点,AC=4,BC=6,则CD的长为 .
7.(2021华师一附中)如图,在口ABCD中,对角线AC,BD交于点E,AC⊥BC,点F是BE的中点,连接CF.若BC=4,CF=2.5,求AB的长.
8.【教材变式】(P61-9改)如图,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是AB的中点.
(1)求∠A的度数;
(2)求证:AE=DE.
B 中档题运用
9.(2020连云港改)如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的处.若∠DBC=26°,则∠A'EB的度数是 .
第9题图
10.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE.则下列结论:①△AOB是等边三角形;②S△AOE=S△COE;③∠AOE=135°;④BC=2AB.其中正确的结论的序号是 _.
第10题图
11.如图,一根长为10的木棍AB斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,B端随之沿地面向右滑行.在此滑动过程中,点O到AB的最大距离为 .
第11题图
12.(2021安顺改)如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:MC=MN;
(2)若AD=2,AN=4,求矩形ABCD的面积.
13.如图,在△ABC中,D是BC上一点,AB=AD,E,F分别是AC,BD的中点,EF=2,求AC的长.
14.(2021广东中考模拟)如图,在矩形ABCD中,以点B为圆心,BC的长为半径画弧交AD于点E,再分别以点C,E为圆心,大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G.
(1)求证:∠AEB=2∠FBC;
(2)若AB=6,BC=10.求CG的长.
C 综合题探究
15.(2021眉山改)如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=6,∠DAC=60°,点F在线段AO上,连接DF,以DF为边作等边△DFE,点E和点A分别位于DF两侧.
(1)求证:∠BDE=∠ADF;
(2)求证:EF=EC.
18.2.1 矩形
第1课时 矩形及其性质
A 基础题夯实
核心知识点1 矩形的性质
1.在矩形ABCD中,AC,BD相交于点O,下列说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=AB D.OA=OB
答案:C
2.矩形的对角线长为10,两邻边之比为3:4,则矩形的周长为 .
答案:28
3.在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=4 cm,则AC的长为 cm.
答案:8
4.(2019福建)如图,点E,F分别是矩形ABCD的边AB,CD上的一点,且DF=BE.求证:AF=CE.
证明:法一:∵四边形ABCD是矩形,∴AD=BC,∠D=∠B=90°.
∵DF=BE,∴△ADF≌△CBE,∴AF=CE;
法二:∵四边形ABCD是矩形,∴AB CD,∵DF=BE.∴CFAE,
∴四边形AFCE为平行四边形,∴AF=CE.
5.(2020毕节改)如图,在矩形ABCD中,AC,BD相交于点O,E,F分别是AO,AD的中点,连接EF,若AB=9 cm,BC=12 cm.求EF的长.
解:∵四边形ABCD是矩形,∴∠ABC=90°,BD=AC,B0=OD,∵AB=9 cm,BC=12 cm,∴AC==15(cm),
∴OD=AC=(cm)∵点E,F分别是AO,AD的中点,
∴EF是△AOD的中位线,.∴EF=OD= cm.
核心知识点2 直角三角形斜边上的中线
6.在Rt△ABC中,∠ACB=90°,D是AB的中点,AC=4,BC=6,则CD的长为 .
答案:
7.(2021华师一附中)如图,在口ABCD中,对角线AC,BD交于点E,AC⊥BC,点F是BE的中点,连接CF.若BC=4,CF=2.5,求AB的长.
解:∵AC⊥BC,点F是BE的中点,∴BE=2CF=5,
∴EC===3,
∵四边形ABCD是平行四边形,
∴AC=2EC=6,∴AB===2.
8.【教材变式】(P61-9改)如图,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是AB的中点.
(1)求∠A的度数;
(2)求证:AE=DE.
解:(1)证∠BCD=∠A,∴∠A+3∠A=90°,∴∠A=22.5°;
(2)连接CE,易证CE=AE=BE,∴∠CED=2∠A=45°,∴CE=DE,
∴AE=DE.
B 中档题运用
9.(2020连云港改)如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的处.若∠DBC=26°,则∠A'EB的度数是 .
第9题图
答案:58°
10.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE.则下列结论:①△AOB是等边三角形;②S△AOE=S△COE;③∠AOE=135°;④BC=2AB.其中正确的结论的序号是 _.
第10题图
答案:①②③
11.如图,一根长为10的木棍AB斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,B端随之沿地面向右滑行.在此滑动过程中,点O到AB的最大距离为 .
第11题图
答案:5
12.(2021安顺改)如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:MC=MN;
(2)若AD=2,AN=4,求矩形ABCD的面积.
解:(1)在矩形ABCD中,∠D=90°,DC//AB,∴∠BAN=∠AMD,
∵BN⊥AM,∴∠BNA=90°=∠D,∵AM=AB,∴△ABN≌△MAD(AAS),
∴AN=DM,∵AM=AB=CD,∴MC=MN;
(2)∵BN=AD=2,AN=4,∴AB==2,∴S矩形ABCD=2×2=4.
13.如图,在△ABC中,D是BC上一点,AB=AD,E,F分别是AC,BD的中点,EF=2,求AC的长.
解:连接AF.∵AB=AD,F是BD的中点,∴AF⊥BD.
∵在Rt△ACF中,∠AFC=90°,E是AC的中点,EF=2,∴AC=2EF=4.
14.(2021广东中考模拟)如图,在矩形ABCD中,以点B为圆心,BC的长为半径画弧交AD于点E,再分别以点C,E为圆心,大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G.
(1)求证:∠AEB=2∠FBC;
(2)若AB=6,BC=10.求CG的长.
解:(1)∵四边形ABCD为矩形,∴AD//BC,∴∠AEB=∠EBC.
根据作图过程可知BF是∠EBC的平分线,
∴∠EBC=2∠FBC,∴∠AEB=2∠FBC;
(2)连接EG,∵BE=BC,∠EBG=∠CBG,BG=BG,∴△EBG≌△CBG,.∴设EG=CG=x.
∵四边形ABCD为矩形,∴CD=AB=6,AD=BC=10,∠A=∠D=90°,
∴AE==8,∴ED=AD-AE=2.∵∠D=90°,DG=CD-CG=6-x,
∴ED2+DG2=EG2,∴22+(6-x)2=x2,∴x=.∴CG=.
C 综合题探究
15.(2021眉山改)如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=6,∠DAC=60°,点F在线段AO上,连接DF,以DF为边作等边△DFE,点E和点A分别位于DF两侧.
(1)求证:∠BDE=∠ADF;
(2)求证:EF=EC.
证明:(1)∵四边形ABCD是矩形,∴OA=OB=OC=OD,
∵∠DAC=60°,∴△OAD为等边三角形,
∴∠DOA=∠DAO=∠ODA=60°,AD=OD,
∵△DFE为等边三角形,∴∠EDF=60°,DF=DE=EF,
∵∠BDE+∠FDO=∠ADF+∠FDO=60°,∴∠BDE=∠ADF;
(2)连接OE,由(1)知,AD=OD,∠ADF=∠BDE,DF=DE,∴△ADF≌△ODE,
∴∠DOE=∠DAF=60°.∵∠DOA=60°,∴∠COE=60°=∠DOE.
∵四边形ABCD为矩形,∴AC=BD,OD=BD,OC=AC,∴OD=OC,
∵OE=OE,∴△ODE≌△OCE,∴EC=ED=EF.
