北师大版数学八年级下册第一章 三角形的证明:1.3_第2课时_线段的垂直平分线 课件(共14张PPT)
文档属性
| 名称 | 北师大版数学八年级下册第一章 三角形的证明:1.3_第2课时_线段的垂直平分线 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 441.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-09 20:01:13 | ||
图片预览





文档简介
(共14张PPT)
1.3 线段的垂直平分线
(第2课时)
1.通过操作、发现、证明等探究,掌握三角形三边垂直平分线的性质证明;
2.通过观察、发现、作图等活动,能用尺规作出等腰三角形和过点作已知直线的垂线;
3.通过实际问题的解决,体会线段垂直平分线的性质和判定定理的应用,提升学生知识迁移的能力.
学习目标
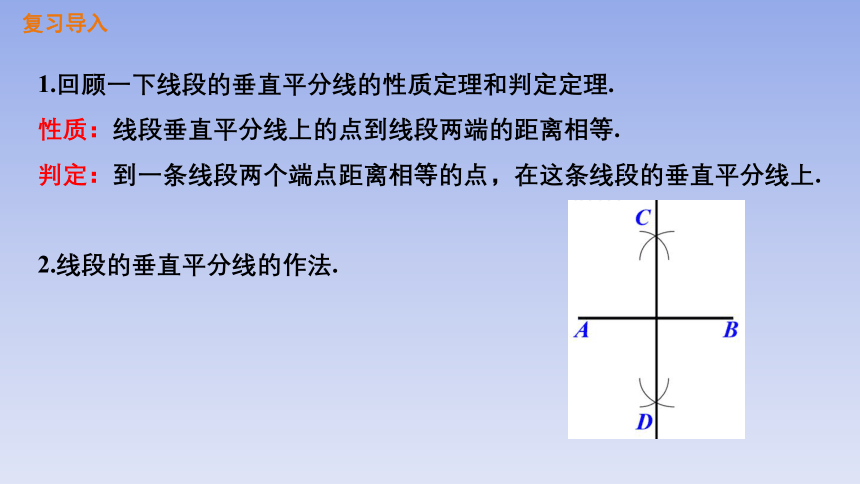
1.回顾一下线段的垂直平分线的性质定理和判定定理.
性质:线段垂直平分线上的点到线段两端的距离相等.
判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
2.线段的垂直平分线的作法.
复习导入
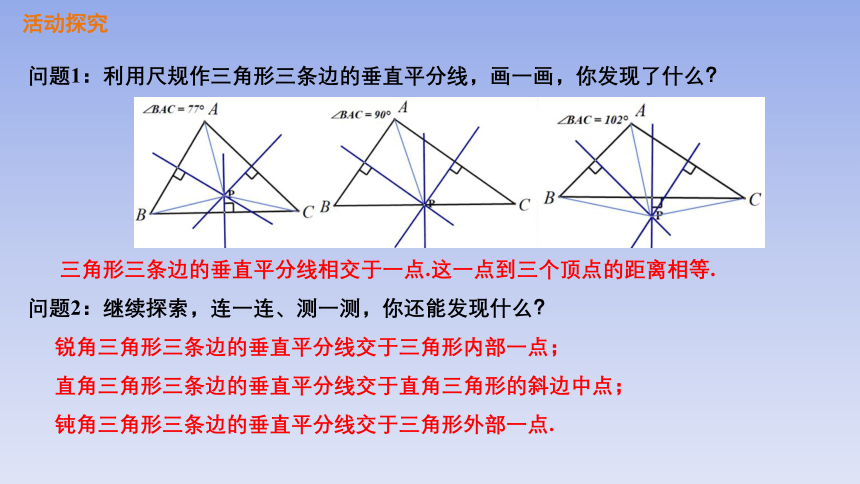
问题1:利用尺规作三角形三条边的垂直平分线,画一画,你发现了什么?
三角形三条边的垂直平分线相交于一点.这一点到三个顶点的距离相等.
问题2:继续探索,连一连、测一测,你还能发现什么?
锐角三角形三条边的垂直平分线交于三角形内部一点;
直角三角形三条边的垂直平分线交于直角三角形的斜边中点;
钝角三角形三条边的垂直平分线交于三角形外部一点.
活动探究
问题3 求证:三角形三条边的垂直平分线相交于一点,这一点到三个顶点的距离相等.
(提示:“三线交于一点”的证明思路:两条直线的交点在第三条直线上. 方法:应用垂直平分线的性质和判定定理.先独立画图、思考2分钟,再小组讨论,确定方法)
已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P.
求证:边AC垂直平分线经过点P,且PA=PB=PC.
画图
写出已知、求证
证明
活动探究
求证:三角形三条边的垂直平分线相交于一点.,这一点到三个顶点的距离相等.
已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P.
求证:边AC垂直平分线经过点P,且PA=PB=PC.
证明:∵点P在线段AB的垂直平分线上.
∴PA=PB(线段垂直平分线上的点到这条线段的两个端点的距离相等).
同理,PB=PC,
∴ PA=PB=PC.
∴点P在线段AC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),
即 边AC的垂直平分线经过点P.
活动探究
问题4(1)已知三角形的一条边及这条边上的高,你能画出满足条件的三角形吗?如果能,能画出几个?所画的三角形都全等吗?
活动探究
(2)已知等腰三角形的底边及其底边上的高,你能用尺规作出满足条件的一个等腰三角形吗?画一画、试一试吧!
例3 已知一个等腰三角形的底边及底边上的高,求作这个等腰三角形.(请独立完成,时间3分钟,提示:完整的作图过程.)
活动探究
问题5 小明通过刚刚学习的线段垂直平分线的知识解决了下面问题:
已知直线l和l上的一点P,用尺规作l垂线,使它经过点P. 你能明白他的作法吗?想一想,说一说吧.
追问:你还有和小明不同的方法吗?做一做,分享一下.
活动探究
问题6 向小明学习,独立解决下面问题:
已知直线l和线外一点P,利用尺规作l垂线,使它经过点P. 说说你的作法,与同伴交流.
活动探究
1.下列说法错误的是( )
A. 三角形三条边的垂直平分线必交于一点.
B. 如果等腰三角形内一点到底边两端点的距离相等,那么过这点与顶点的直线必垂直于底边.
C. 平面上只存在一点到已知三角形三个顶点距离相等.
D. 三角形关于任一边上的垂直平分线成轴对称.
D
灵活运用
2. 如图所示,在△ABC中,∠B=22.5°,AB的垂直平分线交BC于点D,DF⊥AC于点F,并与BC边上的高AE交于G.
求证:EG=EC.
灵活运用
谈谈你本节课的收获吧!
认识知识
积累经验
运用知识
课堂小结
完成本节课课后习题.
课后作业
1.3 线段的垂直平分线
(第2课时)
1.通过操作、发现、证明等探究,掌握三角形三边垂直平分线的性质证明;
2.通过观察、发现、作图等活动,能用尺规作出等腰三角形和过点作已知直线的垂线;
3.通过实际问题的解决,体会线段垂直平分线的性质和判定定理的应用,提升学生知识迁移的能力.
学习目标
1.回顾一下线段的垂直平分线的性质定理和判定定理.
性质:线段垂直平分线上的点到线段两端的距离相等.
判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
2.线段的垂直平分线的作法.
复习导入
问题1:利用尺规作三角形三条边的垂直平分线,画一画,你发现了什么?
三角形三条边的垂直平分线相交于一点.这一点到三个顶点的距离相等.
问题2:继续探索,连一连、测一测,你还能发现什么?
锐角三角形三条边的垂直平分线交于三角形内部一点;
直角三角形三条边的垂直平分线交于直角三角形的斜边中点;
钝角三角形三条边的垂直平分线交于三角形外部一点.
活动探究
问题3 求证:三角形三条边的垂直平分线相交于一点,这一点到三个顶点的距离相等.
(提示:“三线交于一点”的证明思路:两条直线的交点在第三条直线上. 方法:应用垂直平分线的性质和判定定理.先独立画图、思考2分钟,再小组讨论,确定方法)
已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P.
求证:边AC垂直平分线经过点P,且PA=PB=PC.
画图
写出已知、求证
证明
活动探究
求证:三角形三条边的垂直平分线相交于一点.,这一点到三个顶点的距离相等.
已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P.
求证:边AC垂直平分线经过点P,且PA=PB=PC.
证明:∵点P在线段AB的垂直平分线上.
∴PA=PB(线段垂直平分线上的点到这条线段的两个端点的距离相等).
同理,PB=PC,
∴ PA=PB=PC.
∴点P在线段AC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),
即 边AC的垂直平分线经过点P.
活动探究
问题4(1)已知三角形的一条边及这条边上的高,你能画出满足条件的三角形吗?如果能,能画出几个?所画的三角形都全等吗?
活动探究
(2)已知等腰三角形的底边及其底边上的高,你能用尺规作出满足条件的一个等腰三角形吗?画一画、试一试吧!
例3 已知一个等腰三角形的底边及底边上的高,求作这个等腰三角形.(请独立完成,时间3分钟,提示:完整的作图过程.)
活动探究
问题5 小明通过刚刚学习的线段垂直平分线的知识解决了下面问题:
已知直线l和l上的一点P,用尺规作l垂线,使它经过点P. 你能明白他的作法吗?想一想,说一说吧.
追问:你还有和小明不同的方法吗?做一做,分享一下.
活动探究
问题6 向小明学习,独立解决下面问题:
已知直线l和线外一点P,利用尺规作l垂线,使它经过点P. 说说你的作法,与同伴交流.
活动探究
1.下列说法错误的是( )
A. 三角形三条边的垂直平分线必交于一点.
B. 如果等腰三角形内一点到底边两端点的距离相等,那么过这点与顶点的直线必垂直于底边.
C. 平面上只存在一点到已知三角形三个顶点距离相等.
D. 三角形关于任一边上的垂直平分线成轴对称.
D
灵活运用
2. 如图所示,在△ABC中,∠B=22.5°,AB的垂直平分线交BC于点D,DF⊥AC于点F,并与BC边上的高AE交于G.
求证:EG=EC.
灵活运用
谈谈你本节课的收获吧!
认识知识
积累经验
运用知识
课堂小结
完成本节课课后习题.
课后作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
