2021-2022学年高一下学期数学北师大版(2019)必修第二册5.1复数的概念及其几何意义专题课课件(38张ppt)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修第二册5.1复数的概念及其几何意义专题课课件(38张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-09 17:11:50 | ||
图片预览











文档简介
(共38张PPT)
§5.1复数的概念及其几何意义
(专题课)
北师大(2019)必修2
题组与解读
题组一复数的有关概念
题组一 复数的有关概念
解析
1.(2020黑龙江哈尔滨六中高三第二次模拟)复数z=3-2i的虚部为()
A.2 B.-2 C.-2i D.2i
题组一 复数的有关概念
解析
解读
1
复数的实部和虚部都是实数,i是虚数单位。
题组一 复数的有关概念
解析
2.(2020广东实验中学高二下期中)若复数 1)i(i为虚数单位)是纯虚数,则实数a的值是()
A.-1或1 B.1 C.-1 D.0
题组一 复数的有关概念
解析
解读
2
纯虚数条件:实部为零,虚部不为零
题组一 复数的有关概念
解析
3.已知复数 是实数,则实数a的值为()
A.1或-1 B.1
C.-1 D.0或-1
题组一 复数的有关概念
解析
解读
3
实数条件:实部有意义,虚部为零
题组一 复数的有关概念
解析
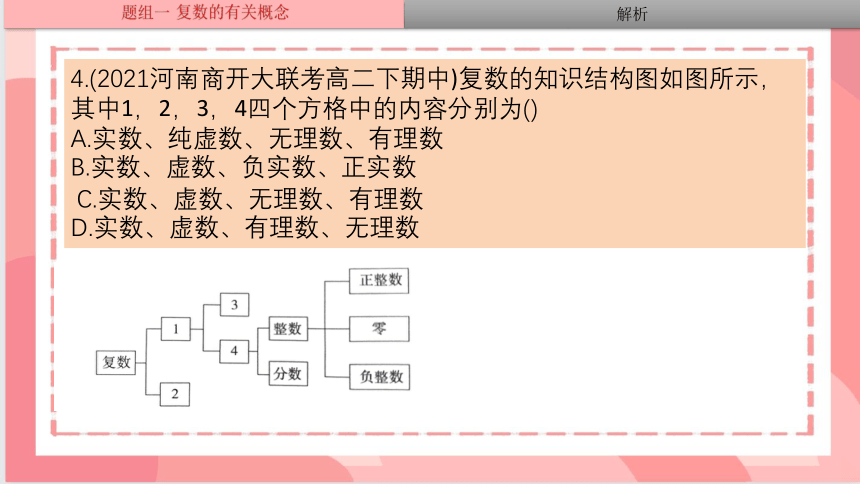
4.(2021河南商开大联考高二下期中)复数的知识结构图如图所示,其中1,2,3,4四个方格中的内容分别为()
A.实数、纯虚数、无理数、有理数
B.实数、虚数、负实数、正实数
C.实数、虚数、无理数、有理数
D.实数、虚数、有理数、无理数
题组一 复数的有关概念
解析
解读
4
这张图反映了数的分类
题组一 复数的有关概念
解析
5.复数 且 若z是实数,则θ的值为_;若z为纯虚数,则θ的值为_____
题组一 复数的有关概念
解析
解读
5
复数的分类和解三角方程(角有限)
题组一 复数的有关概念
解析
6.若 则实数x的值是_
题组一 复数的有关概念
解析
解读
6
能比较大小一定是实数;对数不等式要附加定义域
题组一 复数的有关概念
解析
7.(2020重庆七校联盟高二上联考)求实数m为何值时,复数 是(1)实数;(2)纯虚数.
题组一 复数的有关概念
解析
解读
7
一方面考虑分类,另一方面保证有意义
题组二 复数相等
解析
8.(2021河南郑州高二下期末)若复数 +bi(a,b∈R),=,则符合条件的点(a,b) ( )
A.有1个 B.有2个
C.在直线y=x上 D.不确定
题组二 复数相等
解析
解读
8
复数相等:实部与实部相等,虚部与虚部相等
题组二 复数相等
解析
9.(2020安徽定远育才实验学校高二下月考)已知复数 m为实数,若=,则m的值为()
A.4 B.-1 C.6 D.0
题组二 复数相等
解析
解读
9
复数相等:实部与实部相等,虚部与虚部相等
题组二 复数相等
解析
10.(2020江苏泰州高三下调研测试)若实数x,y满足x+yi=-1+(x-y)i(i是虚数单位),则xy=_.
题组二 复数相等
解析
解读
10
复数相等:实部与实部相等,虚部与虚部相等
题组三 复数的几何意义
解析
11.若复数z=3-i,则z在复平面内对应的点位于()
A.第一象限 B.第二象限
C.第三象限 D.第四象限
题组三 复数的几何意义
解析
解读
11
复数与复平面内的点一一对应
题组三 复数的几何意义
解析
12.已知复数z=(m-3)+(m-1)i的模等于2,则实数m的值为 ()
A.1或3 B.1 C.3 D.2
题组三 复数的几何意义
解析
解读
12
模的公式是
题组三 复数的几何意义
解析
13.(2020四川成都高三第一次诊断性检测)若复数z,与 (i为虚数单位)在复平面内对应的点关于实轴对称,则 ()
A.-3i B.-3+i C.3+i D.3-i
题组三 复数的几何意义
解析
解读
13
实轴就是复平面内的x轴
题组三 复数的几何意义
解析
14.(2019陕西西安高三第一次模拟考试)已知复数z= 与 +(n-2)i互为共轭复数,其中m,n∈R,i为虚数单位,则 ()
A.1 D.
题组三 复数的几何意义
解析
解读
14
共轭复数:实部相等虚部相反
学以致用
1
2
3
4
5
1.(2020河南郑州第一中学高二下期中,★)若M={1, i,N={-1,3},M∩N={3},则实数m= ( )
A.4 B.-1或4 C.-1或6 D.-1
1
2
3
4
5
2.(2020北京人大附中高二下期中,)若i是虚数单位, i=l-3-4il,则实数a= ( )
A.-1 B.-2 C.2 D.3
1
2
3
4
5
3.(2020浙江杭州学军中学高二下期末)已知复数 和 (λ+3sin i(λ ∈R),若=试求λ的取值范围.
1
2
3
4
5
4.(2020天津南开中学高二下期中,)已知复平面内O是原点,向量 对应的复数分别为2-3i,-3+2i,那么向量对应的复数是()
A.-5+5i B.5-5i
C.5+5i D.-5-5i
1
2
3
4
5
5.(2020江西南昌二中高三月考,趁)若复数 ∈R)在复平面内对应的点在直线x+y=0上,则lzl= ( )
A.2 C.1 D.2
§5.1复数的概念及其几何意义
(专题课)
北师大(2019)必修2
题组与解读
题组一复数的有关概念
题组一 复数的有关概念
解析
1.(2020黑龙江哈尔滨六中高三第二次模拟)复数z=3-2i的虚部为()
A.2 B.-2 C.-2i D.2i
题组一 复数的有关概念
解析
解读
1
复数的实部和虚部都是实数,i是虚数单位。
题组一 复数的有关概念
解析
2.(2020广东实验中学高二下期中)若复数 1)i(i为虚数单位)是纯虚数,则实数a的值是()
A.-1或1 B.1 C.-1 D.0
题组一 复数的有关概念
解析
解读
2
纯虚数条件:实部为零,虚部不为零
题组一 复数的有关概念
解析
3.已知复数 是实数,则实数a的值为()
A.1或-1 B.1
C.-1 D.0或-1
题组一 复数的有关概念
解析
解读
3
实数条件:实部有意义,虚部为零
题组一 复数的有关概念
解析
4.(2021河南商开大联考高二下期中)复数的知识结构图如图所示,其中1,2,3,4四个方格中的内容分别为()
A.实数、纯虚数、无理数、有理数
B.实数、虚数、负实数、正实数
C.实数、虚数、无理数、有理数
D.实数、虚数、有理数、无理数
题组一 复数的有关概念
解析
解读
4
这张图反映了数的分类
题组一 复数的有关概念
解析
5.复数 且 若z是实数,则θ的值为_;若z为纯虚数,则θ的值为_____
题组一 复数的有关概念
解析
解读
5
复数的分类和解三角方程(角有限)
题组一 复数的有关概念
解析
6.若 则实数x的值是_
题组一 复数的有关概念
解析
解读
6
能比较大小一定是实数;对数不等式要附加定义域
题组一 复数的有关概念
解析
7.(2020重庆七校联盟高二上联考)求实数m为何值时,复数 是(1)实数;(2)纯虚数.
题组一 复数的有关概念
解析
解读
7
一方面考虑分类,另一方面保证有意义
题组二 复数相等
解析
8.(2021河南郑州高二下期末)若复数 +bi(a,b∈R),=,则符合条件的点(a,b) ( )
A.有1个 B.有2个
C.在直线y=x上 D.不确定
题组二 复数相等
解析
解读
8
复数相等:实部与实部相等,虚部与虚部相等
题组二 复数相等
解析
9.(2020安徽定远育才实验学校高二下月考)已知复数 m为实数,若=,则m的值为()
A.4 B.-1 C.6 D.0
题组二 复数相等
解析
解读
9
复数相等:实部与实部相等,虚部与虚部相等
题组二 复数相等
解析
10.(2020江苏泰州高三下调研测试)若实数x,y满足x+yi=-1+(x-y)i(i是虚数单位),则xy=_.
题组二 复数相等
解析
解读
10
复数相等:实部与实部相等,虚部与虚部相等
题组三 复数的几何意义
解析
11.若复数z=3-i,则z在复平面内对应的点位于()
A.第一象限 B.第二象限
C.第三象限 D.第四象限
题组三 复数的几何意义
解析
解读
11
复数与复平面内的点一一对应
题组三 复数的几何意义
解析
12.已知复数z=(m-3)+(m-1)i的模等于2,则实数m的值为 ()
A.1或3 B.1 C.3 D.2
题组三 复数的几何意义
解析
解读
12
模的公式是
题组三 复数的几何意义
解析
13.(2020四川成都高三第一次诊断性检测)若复数z,与 (i为虚数单位)在复平面内对应的点关于实轴对称,则 ()
A.-3i B.-3+i C.3+i D.3-i
题组三 复数的几何意义
解析
解读
13
实轴就是复平面内的x轴
题组三 复数的几何意义
解析
14.(2019陕西西安高三第一次模拟考试)已知复数z= 与 +(n-2)i互为共轭复数,其中m,n∈R,i为虚数单位,则 ()
A.1 D.
题组三 复数的几何意义
解析
解读
14
共轭复数:实部相等虚部相反
学以致用
1
2
3
4
5
1.(2020河南郑州第一中学高二下期中,★)若M={1, i,N={-1,3},M∩N={3},则实数m= ( )
A.4 B.-1或4 C.-1或6 D.-1
1
2
3
4
5
2.(2020北京人大附中高二下期中,)若i是虚数单位, i=l-3-4il,则实数a= ( )
A.-1 B.-2 C.2 D.3
1
2
3
4
5
3.(2020浙江杭州学军中学高二下期末)已知复数 和 (λ+3sin i(λ ∈R),若=试求λ的取值范围.
1
2
3
4
5
4.(2020天津南开中学高二下期中,)已知复平面内O是原点,向量 对应的复数分别为2-3i,-3+2i,那么向量对应的复数是()
A.-5+5i B.5-5i
C.5+5i D.-5-5i
1
2
3
4
5
5.(2020江西南昌二中高三月考,趁)若复数 ∈R)在复平面内对应的点在直线x+y=0上,则lzl= ( )
A.2 C.1 D.2
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
