初中数学几何(圆)填空题中的多解问题(有答案)
文档属性
| 名称 | 初中数学几何(圆)填空题中的多解问题(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 66.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-03 00:00:00 | ||
图片预览




文档简介
课件20张PPT。缜密思维 准确计算———几何填空题中的多解问题练习、(1)任意画一个三角形。
(2)?ABC内接于⊙O,∠BOC=110?,
则∠A=————。
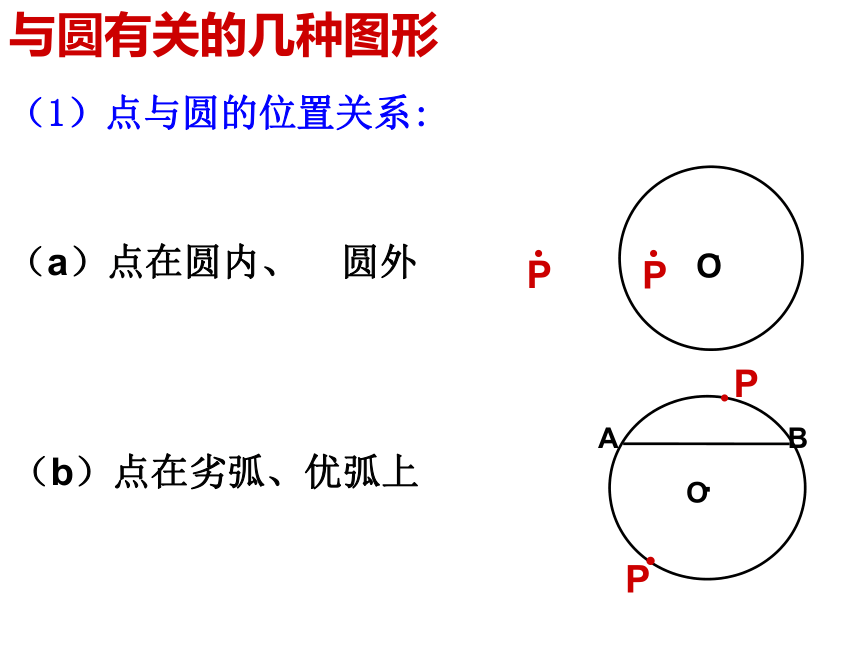
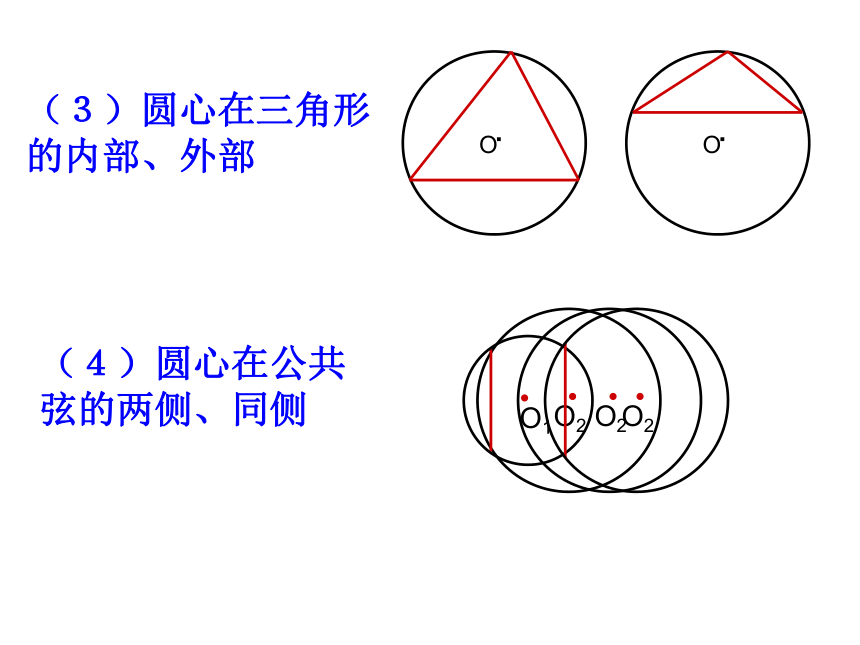
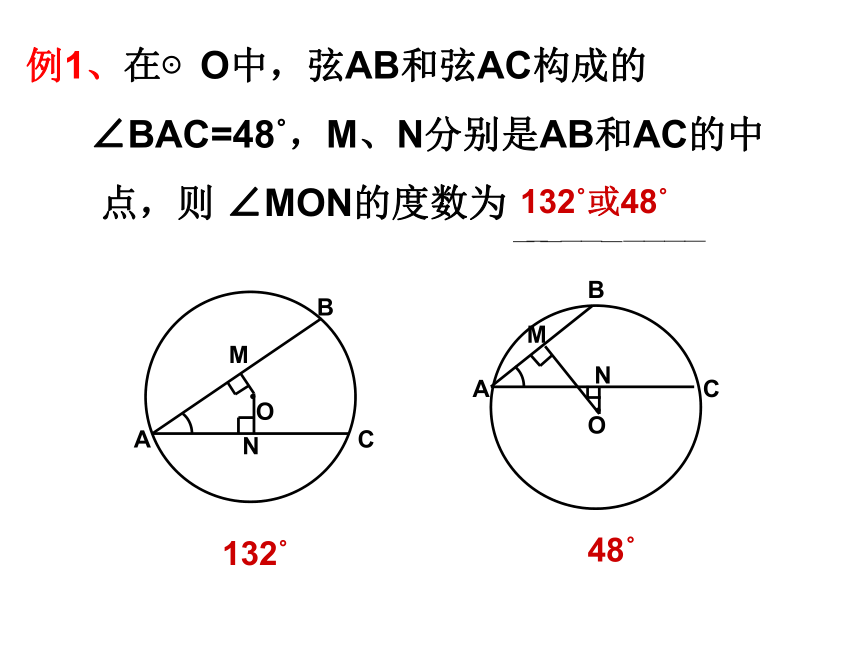
∠A=55?55?∠A=125?550或1250错误原因:(2)基本概念理解不透彻如:两圆若相切,分为内切和外切。(1)受习惯性思维的影响如:三角形常画成锐角三角形。 从而导致画与圆有关的图形时由于概念不清,分类不明,及习惯性思维,遗漏某种图形产生丢解。与圆有关的几种图形(1)点与圆的位置关系:(2)图形与圆心的位置关系·O·O(3)圆心在三角形的内部、外部例1、在⊙O中,弦AB和弦AC构成的
∠BAC=48?,M、N分别是AB和AC的中
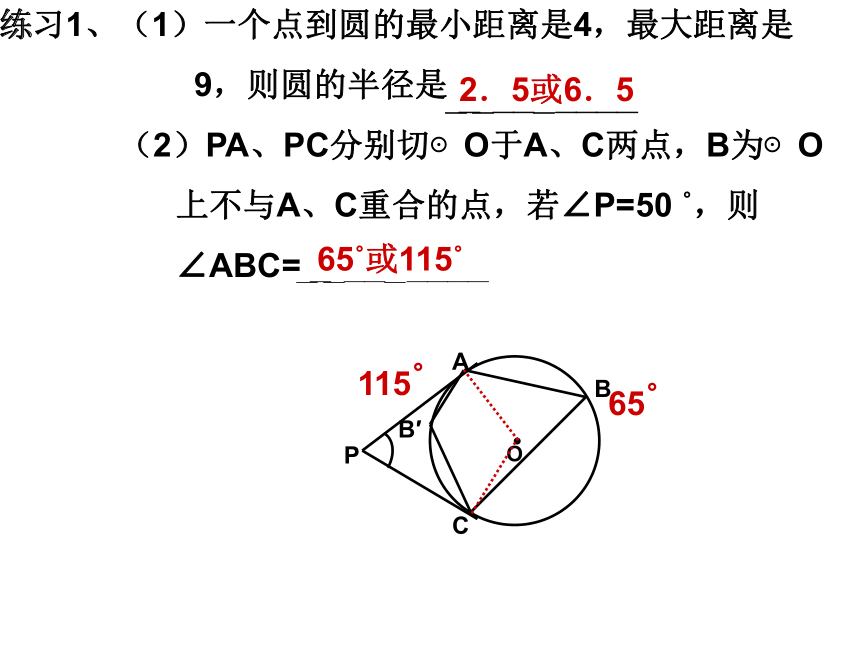
点,则 ∠MON的度数为132?48?132?或48?练习1、(1)一个点到圆的最小距离是4,最大距离是
9,则圆的半径是
(2)PA、PC分别切⊙O于A、C两点,B为⊙O
上不与A、C重合的点,若∠P=50 ?,则
∠ABC=
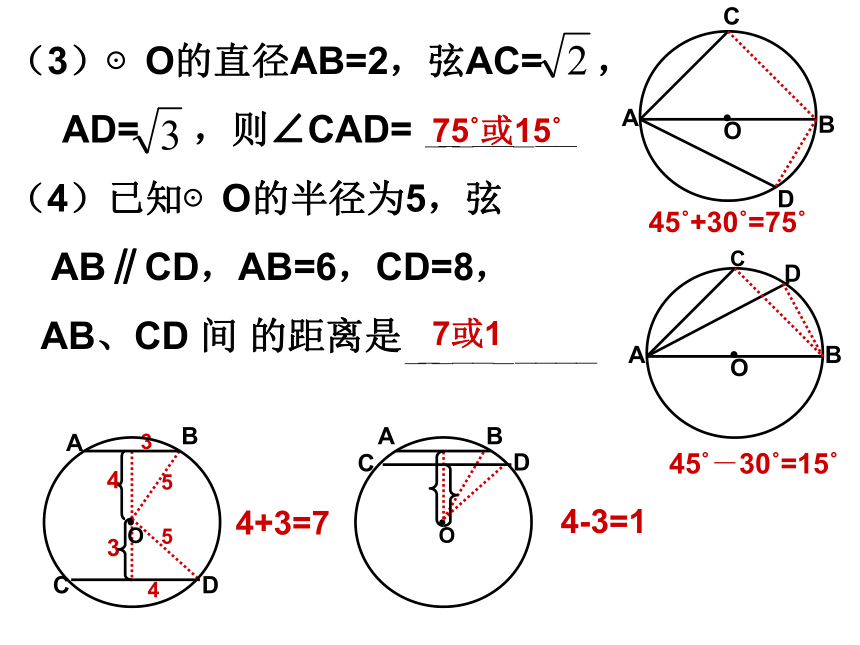
65?115?65?或115?2.5或6.5(3)⊙O的直径AB=2,弦AC= ,
AD= ,则∠CAD=
(4)已知⊙O的半径为5,弦
AB∥CD,AB=6,CD=8,
AB、CD 间 的距离是45?+30?=75?45?-30?=15?75?或15?4+3=74-3=17或1例2、等腰△ABC的外接圆半径为3,圆心O到底边
BC的距离为1,则S ABC=△AD=3+1=4AD=3-1=2练习2、(1)水平放置的圆柱形排水管的截面半
径为1,水面宽也为1,则截面上有水的弓形
的面积为例3、已知相交两圆的公共弦长为24,两圆半径
分别为15和20,则两圆的圆 心距为
O1O2=O2C+O1CO1O2=O2C-O1C25或7=16+9=25=16-9=7练习3、(1) 若⊙O1与⊙O2相交于A、B两点,
且⊙O1、⊙O2的半径分别为 、2,公共弦
长为2,则∠O1AO2度数是∠O1AO2=60?+45?=105?∠O1AO2=60?-45?=15?105?或15?例4、(1) ⊙O 的半径为5, AB是直径,点C
在⊙O上,过点C引 AB的垂线,垂足为D,点
D 分直径为2:3两部分,则BC=
练习4、⊙O的弦AB=2 ,过圆心的直线与
AB垂直相交于C,交⊙O于点D,且
OC=1,则CD=R=2CD =2-1=1CD′=2+1=31或3 综合练习
(2)若圆的一条弦长等于半径,则弦所对的弧的
度数是
(3)圆的半径为5,圆内接梯形的两底分别为6和
8,则梯形面积是
(4)一张矩形纸片,长8,宽6,用它做一个圆柱
的侧面,则相应圆柱的底面积 是
60?或300?49或7 (1)半径为2和4的两圆相切,则这两圆的圆心
距为2或6(5)以正方形ABCD的边CD为边作正三角形
CDP,则∠APB=30?或150?小结:(1)对于某些填空题或解答题,在没有给出图形
的情况下可能出现多解。(2)充分考虑各种情况,画出每种情况下的图
形,再进行解答。(3)数学基本概念是理论依据。牢固掌握
基本概念。(4)体现了数学的分类思想。 思考题: 已知半径不等的⊙O1、⊙O2外离,线段
O1O2分别交⊙O1、O2 于点A、 B,MN为两
圆的公切线,分别切⊙O1⊙O2于M、N,连接
MA、NB。判断∠AMN与∠BNM的数量关系,
并证明你的判断。∠AMN=∠BNM∠AMN+∠BNM=90?(1)若圆的半径为2,一条弦长为2 ,则弦所对的
弧长为(4)△ABC中,∠A=56?,H为△ABC的垂心,
则 ∠BHC=(3) ⊙O1和⊙O2交于A、B两点,且⊙O1经过点
O2,若∠AO1B=90?,则∠AO2B的度数是(2) 圆的半径为5,弦AB的长为6,则弓形的高
是作业
(2)?ABC内接于⊙O,∠BOC=110?,
则∠A=————。
∠A=55?55?∠A=125?550或1250错误原因:(2)基本概念理解不透彻如:两圆若相切,分为内切和外切。(1)受习惯性思维的影响如:三角形常画成锐角三角形。 从而导致画与圆有关的图形时由于概念不清,分类不明,及习惯性思维,遗漏某种图形产生丢解。与圆有关的几种图形(1)点与圆的位置关系:(2)图形与圆心的位置关系·O·O(3)圆心在三角形的内部、外部例1、在⊙O中,弦AB和弦AC构成的
∠BAC=48?,M、N分别是AB和AC的中
点,则 ∠MON的度数为132?48?132?或48?练习1、(1)一个点到圆的最小距离是4,最大距离是
9,则圆的半径是
(2)PA、PC分别切⊙O于A、C两点,B为⊙O
上不与A、C重合的点,若∠P=50 ?,则
∠ABC=
65?115?65?或115?2.5或6.5(3)⊙O的直径AB=2,弦AC= ,
AD= ,则∠CAD=
(4)已知⊙O的半径为5,弦
AB∥CD,AB=6,CD=8,
AB、CD 间 的距离是45?+30?=75?45?-30?=15?75?或15?4+3=74-3=17或1例2、等腰△ABC的外接圆半径为3,圆心O到底边
BC的距离为1,则S ABC=△AD=3+1=4AD=3-1=2练习2、(1)水平放置的圆柱形排水管的截面半
径为1,水面宽也为1,则截面上有水的弓形
的面积为例3、已知相交两圆的公共弦长为24,两圆半径
分别为15和20,则两圆的圆 心距为
O1O2=O2C+O1CO1O2=O2C-O1C25或7=16+9=25=16-9=7练习3、(1) 若⊙O1与⊙O2相交于A、B两点,
且⊙O1、⊙O2的半径分别为 、2,公共弦
长为2,则∠O1AO2度数是∠O1AO2=60?+45?=105?∠O1AO2=60?-45?=15?105?或15?例4、(1) ⊙O 的半径为5, AB是直径,点C
在⊙O上,过点C引 AB的垂线,垂足为D,点
D 分直径为2:3两部分,则BC=
练习4、⊙O的弦AB=2 ,过圆心的直线与
AB垂直相交于C,交⊙O于点D,且
OC=1,则CD=R=2CD =2-1=1CD′=2+1=31或3 综合练习
(2)若圆的一条弦长等于半径,则弦所对的弧的
度数是
(3)圆的半径为5,圆内接梯形的两底分别为6和
8,则梯形面积是
(4)一张矩形纸片,长8,宽6,用它做一个圆柱
的侧面,则相应圆柱的底面积 是
60?或300?49或7 (1)半径为2和4的两圆相切,则这两圆的圆心
距为2或6(5)以正方形ABCD的边CD为边作正三角形
CDP,则∠APB=30?或150?小结:(1)对于某些填空题或解答题,在没有给出图形
的情况下可能出现多解。(2)充分考虑各种情况,画出每种情况下的图
形,再进行解答。(3)数学基本概念是理论依据。牢固掌握
基本概念。(4)体现了数学的分类思想。 思考题: 已知半径不等的⊙O1、⊙O2外离,线段
O1O2分别交⊙O1、O2 于点A、 B,MN为两
圆的公切线,分别切⊙O1⊙O2于M、N,连接
MA、NB。判断∠AMN与∠BNM的数量关系,
并证明你的判断。∠AMN=∠BNM∠AMN+∠BNM=90?(1)若圆的半径为2,一条弦长为2 ,则弦所对的
弧长为(4)△ABC中,∠A=56?,H为△ABC的垂心,
则 ∠BHC=(3) ⊙O1和⊙O2交于A、B两点,且⊙O1经过点
O2,若∠AO1B=90?,则∠AO2B的度数是(2) 圆的半径为5,弦AB的长为6,则弓形的高
是作业
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
