2.1简谐运动精选训练题 同步练习(Word版含解析)
文档属性
| 名称 | 2.1简谐运动精选训练题 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 479.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-09 02:47:33 | ||
图片预览



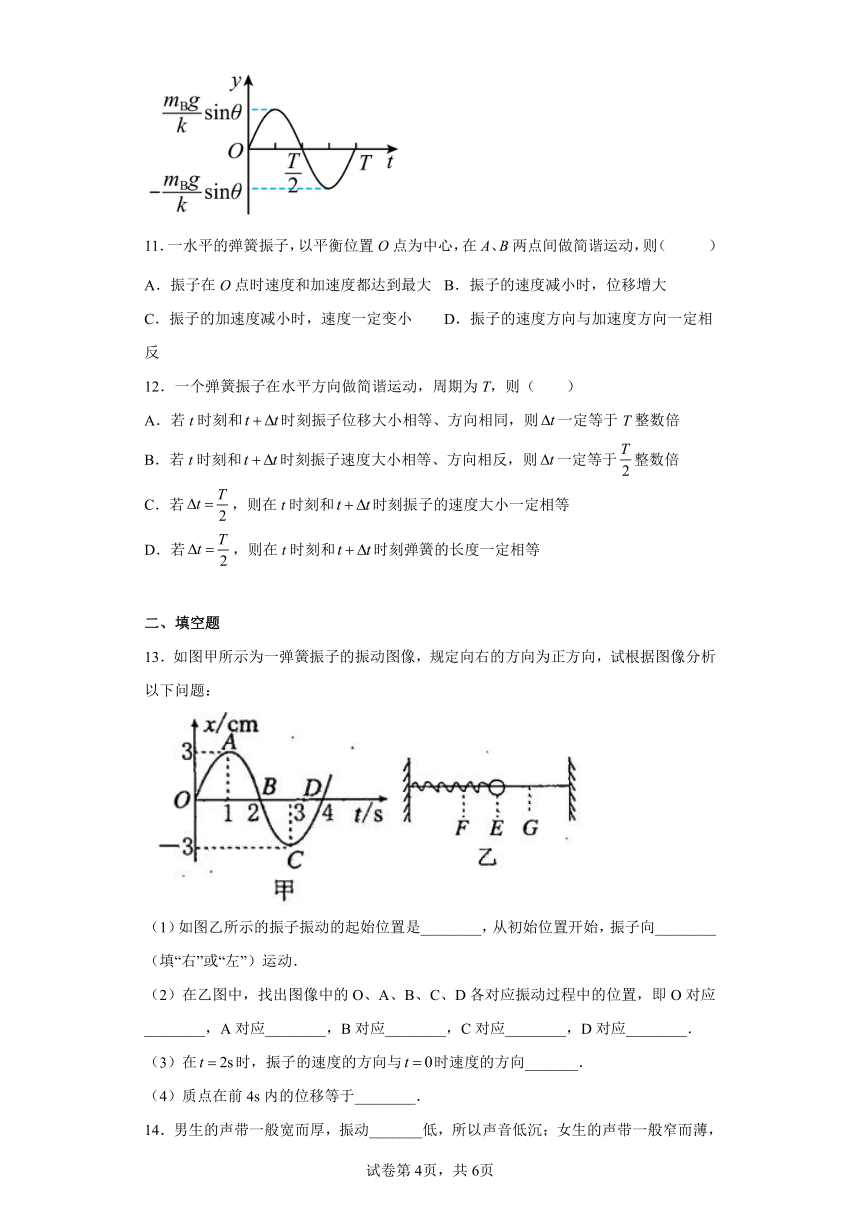
文档简介
人教版(2019)选择性必修一 2.1 简谐运动 精选训练题
一、单选题
1.关于简谐运动的位移、速度、加速度的关系,下列说法中正确的是( )
A.位移减小时,加速度增大,速度也增大
B.位移方向总跟加速度方向相反,跟速度方向相同
C.物体向平衡位置运动时,速度方向跟位移方向相反
D.物体向平衡位置运动时,做匀加速运动
2.关于简谐运动的下列说法中,正确的是( )
A.位移减小时,加速度增大,速度减小
B.位移方向总跟加速度方向相反,跟速度方向相同
C.物体的运动方向指向平衡位置时,速度方向跟位移方向相反;背向平衡位置时,速度方向跟位移方向相同
D.水平弹簧振子朝左运动时,加速度方向跟速度方向相同,朝右运动时,加速度方向跟速度方向相反
3.一做简谐运动的弹簧振子,其质量为m,最大速率为v0。若从某时刻算起,在半个周期内,合外力( )
A.做功一定为0 B.做功一定不为0
C.做功一定是mv02 D.做功可能是0到mv02之间的某一个值
4.简谐振动属于以下哪种运动( )
A.匀速直线运动 B.匀变速直线运动
C.非匀变速运动 D.以上运动都可能
5.如图所示,竖直轻质弹性绳上端固定,原长状态时下端在P点。现取来一块带有小孔的薄板,使小孔处在P点,并将绳下端穿过小孔悬挂一个质量为m的小球,小球静止时位于O点。现将小球拉至与O点等高的A点静止释放,B为A点的对称点,不计一切阻力且弹性绳始终遵循胡克定律。则关于小球释放之后的运动,下列说法正确的是( )
A.小球将沿直线在A、B之间来回运动
B.小球将沿曲线在A、B之间来回运动
C.小球经过P点正下方时绳子拉力大于mg
D.小球的运动不是简谐运动
6.如图所示,倾角为、长度有限的光滑斜面固定在水平面上,一根劲度系数为的轻质弹簧下端固定于斜面底部,上端压一个质量为的小物块,与弹簧间不拴接,开始时处于静止状态。现有另一个质量为的小物块从斜面上某处由静止释放,与发生正碰后立即粘在一起成为组合体。已知弹簧的弹性势能与其形变量的关系为,重力加速度为,弹簧始终未超出弹性限度。下列说法正确的是( )
A.被弹簧反弹后恰好可以回到的释放点
B.整个过程中、和弹簧组成的系统机械能守恒
C.当的释放点到的距离为时,恰好不会与弹簧分离
D.要使能在斜面上做完整的简谐运动,的释放点到的距离至少为
7.如图所示,小球在光滑水平面上以O为平衡位置,在A、B之间做简谐运动,下列说法正确的是( )
A.小球在O点速度最大 B.小球在A点速度最大
C.小球在B点加速度最小 D.小球在B点回复力最小
8.物体产生机械振动的条件是( )
A.有方向不变、大小不变的力作用在物体上
B.有方向不变、大小变化的力作用在物体上
C.有方向变化、大小不变的力作用在物体上
D.有始终指向平衡位置的回复力作用在物体上
9.下列运动中不属于机械振动的是( )
A.树枝在风的作用下运动 B.竖直向上抛出的物体的运动
C.说话时声带的运动 D.爆炸声引起窗扇的运动
10.如图所示,一个劲度系数为k的轻弹簧下端固定在挡板上,上端与物块A连接在一起,物块B紧挨着物块A静止在光滑斜面上。某时刻将B迅速移开,A将在斜面上做简谐运动,已知物块A、B的质量分别为、,若取沿斜面向上为正方向,移开B的时刻为计时起点,则A的振动位移随时间变化的图像是(重力加速度为g)( )
A. B.
C. D.
11.一水平的弹簧振子,以平衡位置O点为中心,在A、B两点间做简谐运动,则( )
A.振子在O点时速度和加速度都达到最大 B.振子的速度减小时,位移增大
C.振子的加速度减小时,速度一定变小 D.振子的速度方向与加速度方向一定相反
12.一个弹簧振子在水平方向做简谐运动,周期为T,则( )
A.若t时刻和时刻振子位移大小相等、方向相同,则一定等于T整数倍
B.若t时刻和时刻振子速度大小相等、方向相反,则一定等于整数倍
C.若,则在t时刻和时刻振子的速度大小一定相等
D.若,则在t时刻和时刻弹簧的长度一定相等
二、填空题
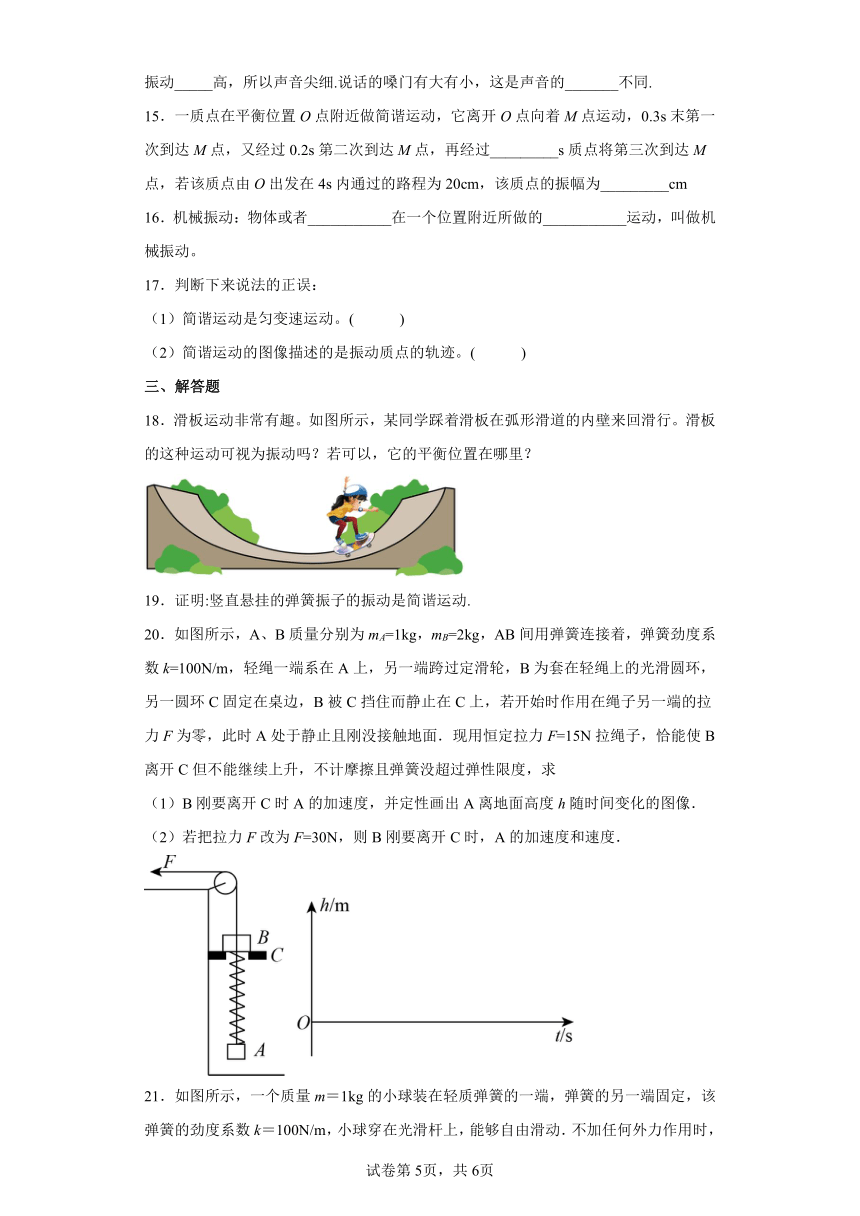
13.如图甲所示为一弹簧振子的振动图像,规定向右的方向为正方向,试根据图像分析以下问题:
(1)如图乙所示的振子振动的起始位置是________,从初始位置开始,振子向________(填“右”或“左”)运动.
(2)在乙图中,找出图像中的O、A、B、C、D各对应振动过程中的位置,即O对应________,A对应________,B对应________,C对应________,D对应________.
(3)在时,振子的速度的方向与时速度的方向_______.
(4)质点在前4s内的位移等于________.
14.男生的声带一般宽而厚,振动_______低,所以声音低沉;女生的声带一般窄而薄,振动_____高,所以声音尖细.说话的嗓门有大有小,这是声音的_______不同.
15.一质点在平衡位置O点附近做简谐运动,它离开O点向着M点运动,0.3s末第一次到达M点,又经过0.2s第二次到达M点,再经过_________s质点将第三次到达M点,若该质点由O出发在4s内通过的路程为20cm,该质点的振幅为_________cm
16.机械振动:物体或者___________在一个位置附近所做的___________运动,叫做机械振动。
17.判断下来说法的正误:
(1)简谐运动是匀变速运动。( )
(2)简谐运动的图像描述的是振动质点的轨迹。( )
三、解答题
18.滑板运动非常有趣。如图所示,某同学踩着滑板在弧形滑道的内壁来回滑行。滑板的这种运动可视为振动吗?若可以,它的平衡位置在哪里?
19.证明:竖直悬挂的弹簧振子的振动是简谐运动.
20.如图所示,A、B质量分别为mA=1kg,mB=2kg,AB间用弹簧连接着,弹簧劲度系数k=100N/m,轻绳一端系在A上,另一端跨过定滑轮,B为套在轻绳上的光滑圆环,另一圆环C固定在桌边,B被C挡住而静止在C上,若开始时作用在绳子另一端的拉力F为零,此时A处于静止且刚没接触地面.现用恒定拉力F=15N拉绳子,恰能使B离开C但不能继续上升,不计摩擦且弹簧没超过弹性限度,求
(1)B刚要离开C时A的加速度,并定性画出A离地面高度h随时间变化的图像.
(2)若把拉力F改为F=30N,则B刚要离开C时,A的加速度和速度.
21.如图所示,一个质量m=1kg的小球装在轻质弹簧的一端,弹簧的另一端固定,该弹簧的劲度系数k=100N/m,小球穿在光滑杆上,能够自由滑动.不加任何外力作用时,小球静止在O点位置.现将小球向右拉至A点,然后由静止释放,小球将做简谐运动,B点是小球向左运动的最远距离.其中OA=10cm,小球运动到A点时弹簧的弹性势能为0.5J,不计其他阻力.求:
(1)小球在B点的位移大小和加速度大小;
(2)小球在振动过程中的最大速度大小.
22.一根弹簧的上端固定,下端系一小球,将小球向下拉一点距离后放手,小球便上下振动起来。试证明这个小球在做简谐运动。(提示:使小球振动的回复力是小球所受到的重力和弹簧弹力的合力)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
A.位移减小时,加速度减小,速度增大。A错误;
B.根据回复力公式可知,位移方向总跟加速度方向相反,跟速度方向可以相同,也可以相反。B错误;
C.物体向平衡位置运动时,速度方向跟位移方向相反,C正确;
D.物体向平衡位置运动时,做加速度减小的加速运动。D错误。
故选C。
2.C
【详解】
A.根据
可知,位移减小时,加速度减小,速度增大,选项A错误;
B.根据
可知,位移方向总跟加速度方向相反,跟速度方向可能相同,也可能相反,选项B错误;
C.物体的运动方向指向平衡位置时,速度方向跟位移方向相反;背向平衡位置时,速度方向跟位移方向相同,选项C正确;
D.水平弹簧振子向平衡位置运动时,加速度方向跟速度方向相同,朝远离平衡位置运动时,加速度方向跟速度方向相反,选项D错误。
故选C。
3.A
【详解】
若从某时刻算起,在半个周期内,振子的速度与开始时等大反向,根据动能定理可知,动能的变化量为零,则合外力的功为零。
故选A。
4.C
【详解】
A.简谐运动的速度是变化的,不可能是匀速直线运动,故A错误;
BCD.简谐运动物体的速度随时间也周期性变化,回复力和加速度随时间作周期性变化,是非匀变速运动,故C正确,BD错误。
故选C。
5.A
【详解】
设PO=h,则
设某时刻弹性绳与竖直方向的夹角为θ,此时球离开O点的距离为x,则弹力的竖直分量
可知合力方向水平,小球将沿直线在A、B之间来回运动;小球受大小为
满足简谐振动的F=-kx的特征,则球的运动是简谐振动;小球经过P点正下方时绳子拉力等于mg。
故选A。
6.C
【详解】
AB.因、碰撞后粘在一起,属于完全非弹性碰撞,整个系统有机械能损失,组合体不可能回到的释放点,故AB错误;
C.静止时,根据平衡条件有
对由机械能守恒定律有
根据动量守恒定律有
从、碰撞结束到向上运动到最高点时弹簧恰好处于原长的过程中,对和弹簧组成的系统由机械能守恒定律有
联立解得
故C正确;
D.要使能在斜面上做完整的简谐运动,能运动到的最高点是弹簧恰好处于原长状态时弹簧顶端所在位置,根据C项中解析可知D错误。
故选C。
7.A
【详解】
由题意小球在光滑水平面上以O为平衡位置,在A、B之间做简谐运动,则O点处小球速度最大,加速度和回复力为零,A、B两点处小球速度为零,加速度和回复力最大。
故选A。
8.D
【详解】
振动需要回复力,回复力应该始终指向平衡位置,故其方向是变化的;回复力大小可以变化,也可以不变化,如果是简谐运动,回复力F=-kx,与位移成正比,不断变化;
故选D。
9.B
【详解】
物体(或物体的某一部分)在某一位置附近的往复运动称为机械振动,树枝的运动、声带的运动以及窗扇的运动均是在其平衡位置附近的振动,只有竖直向上抛出的物体的运动不是在其平衡位置附近的振动。
故选B。
10.B
【详解】
物块A、B紧挨在一起平衡时弹簧压缩量
移走B后,A平衡时弹簧压缩量
因此,负向最大位移为
又时,A在负向最大位移处,故B正确,ACD错误。
故选B。
11.B
【详解】
A.振子通过平衡位置时,速度最大,加速度为零,A错误;
B.振子在平衡位置时速度最大,偏离平衡位置越远速度越小,位移越大,故速度减小时位移增大,B正确;
C.振子在平衡位置时,加速度为零,偏离平衡位置越近加速度越小,速度越大,故加速度减小时速度变大,C错误;
D.振子每次通过同一位置(非最大位移处)时,其加速度方向相同,但速度有两个可能的方向,振子的速度方向与加速度方向可能相同,也可能相反,D错误。
故选B。
12.C
【详解】
A.在t时刻和(t+ t)时刻振子的位移相同,所以这两时刻振子通过同一个位置,而每一个周期内,振子两次出现在同一个位置上,所以当速度方向相同时,则 t可以等于T的整数;当速度方向相反时,则 t不等于T的整数,故A错误;
B.若t时刻和(t+ t)时刻振子运动速度大小相等,方向相反,则 t可能等于的整数倍,也可能大于的整数倍,也可能小于的整数倍,故B错误;
C.若 t=,则在t时刻和(t+ t)时刻振子的位置关于平衡位置对称或经过平衡位置,所以这两时刻速度的大小一定相等,故C正确;
D.若 t=,则在t时刻和(t+ t)时刻振子的位置关于平衡位置对称或经过平衡位置,所以这两时刻位移的大小一定相等,由 知加速度大小一定相等,但弹簧的状态不相同,则长度不相等,故D错误。
故选C。
13. E 右 E G E F E 相反 0
由题中“如图甲所示为一弹簧振子的振动图像”可知,本题考查简谐振动的振动图像,根据简谐振动的振动图像反应的位移与时间的关系.
【详解】
(1)[1]由图知t=0时刻,x=0,说明振子振动的起始位置是E;
[2]t=0时刻位移图像的斜率为正,则振子速度沿正向,即向右;
(2)[3][4][5][6][7]根据位移和起始速度方向可以知道,图像中的O、A、B、C、D各对应振动过程中的位置,即O对应E、A对应G、B对应E、C对应F、D对应E;
(3)[8]在t=2s时,图像的斜率为负,说明振子的速度沿负方向,即向左,t=0速度的方向相反;
(4)[9]质点在前4s内回到了出发点,其位移等于零.
14. 频率 频率 响度
【详解】
[1]男生的声带一般宽而厚,说明声带振动慢,所以频率低;
[2]女生的声带一般窄而薄,说明声带振动快,所以频率高;
[3]响度是声音的三个特征之一,与声音的振幅有关,振幅越大,响度越大,振幅越小,响度越小;题中的“嗓门大小”是说声音的振幅大小,所以声音的响度不同。
此外,声音的另外两个特征分别是音调和音色,音调是指声音的高低,由振动的频率决定;音色反映的是声音的品质与特色,它跟发声体的材料和结构有关。
15. 1.4 2
【详解】
[1]运动过程如图所示,振子第三次通过M点需要经过的时间为;
[2]质点振动周期为,故
解得
16. 物体的一部分 往复
【详解】
[1][2]机械振动:物体或者物体的一部分在一个位置附近所做的往复运动,叫做机械振动。
17. 错 错
【详解】
(1)[1]简谐运动中,回复力随位移的变化而变化,是变力,所以简谐运动是非匀变速运动。故错。
(2)[2]简谐运动的图像描述的是质点的位移随时间变化的规律,不是振动质点的轨迹,故错。
18.可以看成振动;弧形滑道的最低点为平衡位置。
【详解】
可以看成振动,在平衡位置附近的往复运动即为振动,滑板运动在弧形滑道的内壁来回滑行,以弧形滑道的最低点为平衡位置,属于振动。
19.见解析
【详解】
振子处于平衡状态时有
mg=kx0
当振动过程中向下相对平衡位置的位移为x时振子所受的合力为
F=mg-k(x+x0)
联立,可得
F=-kx
符合简谐运动的回复力公式,故为简谐运动。
20.(1)15m/s2,;(2)0,3m/s
【详解】
解:(1)B刚要离开C的时候,弹簧对B的弹力N= mBg,A的受力图如图所示,由牛顿第二定律
mAg+N-F=mAaA
可得
aA==15m/s2
A物体的运动为简谐运动,平衡位置为A所受合力为零的位置,此时弹簧的弹力为5N,弹簧处于压缩,压缩量为0.05m,开始振动时压缩量为,所以振幅L=0.15m。
所以A距离地面高度h随时间t变化的关系式是
h=L-Lcos
则有A离地面高度h随时间变化的图像,如下图所示,
(2)当F=0时,弹簧的伸长量
当F=15N,且A上升到最高点时,弹簧的压缩量
所以A上升的高度
h= x1+ x2=0.3m
A上升过程中
Fh=mAgh+△Ep
所以弹簧弹性势能增加了
△Ep=1.5J
把拉力改为F=30N时,A上升过程中
Fh-mAgh-△Ep=mBv2
解得
v=3m/s
B刚要离开C时,弹簧弹力N= mBg=20N,由牛顿第二定律有
mAg+N-F=mAaA
解得
aA=0
21.(1)0.1m,10 m/s2;(2)1m/s
【详解】
(1)因为振子在做简谐振动,A、B两点关于O点对称.
振子在B点的位移
x=OB=OA=10 cm=0.1m
在B点受力分析可得
FB=kx=ma
解得
a=10 m/s2
(2)振子在O点合力为0,因此在O点速度最大.简谐运动过程中机械能守恒,由A运动到O的过程中,弹性势能转化为动能
可得
解得
v=1m/s
22.见解析
【详解】
设振子的平衡位置为O向下方向为正方向,此时弹簧已经有了一个伸长量h,设弹簧的劲度系数为k由平衡条件得
当振子向下偏离平衡位置的距离为x时,回复力即合外力为
代入得
可见小球所受合外力与它的位移的关系符合简谐运动的特点,这个小球在做简谐运动。
答案第1页,共2页
答案第1页,共2页
一、单选题
1.关于简谐运动的位移、速度、加速度的关系,下列说法中正确的是( )
A.位移减小时,加速度增大,速度也增大
B.位移方向总跟加速度方向相反,跟速度方向相同
C.物体向平衡位置运动时,速度方向跟位移方向相反
D.物体向平衡位置运动时,做匀加速运动
2.关于简谐运动的下列说法中,正确的是( )
A.位移减小时,加速度增大,速度减小
B.位移方向总跟加速度方向相反,跟速度方向相同
C.物体的运动方向指向平衡位置时,速度方向跟位移方向相反;背向平衡位置时,速度方向跟位移方向相同
D.水平弹簧振子朝左运动时,加速度方向跟速度方向相同,朝右运动时,加速度方向跟速度方向相反
3.一做简谐运动的弹簧振子,其质量为m,最大速率为v0。若从某时刻算起,在半个周期内,合外力( )
A.做功一定为0 B.做功一定不为0
C.做功一定是mv02 D.做功可能是0到mv02之间的某一个值
4.简谐振动属于以下哪种运动( )
A.匀速直线运动 B.匀变速直线运动
C.非匀变速运动 D.以上运动都可能
5.如图所示,竖直轻质弹性绳上端固定,原长状态时下端在P点。现取来一块带有小孔的薄板,使小孔处在P点,并将绳下端穿过小孔悬挂一个质量为m的小球,小球静止时位于O点。现将小球拉至与O点等高的A点静止释放,B为A点的对称点,不计一切阻力且弹性绳始终遵循胡克定律。则关于小球释放之后的运动,下列说法正确的是( )
A.小球将沿直线在A、B之间来回运动
B.小球将沿曲线在A、B之间来回运动
C.小球经过P点正下方时绳子拉力大于mg
D.小球的运动不是简谐运动
6.如图所示,倾角为、长度有限的光滑斜面固定在水平面上,一根劲度系数为的轻质弹簧下端固定于斜面底部,上端压一个质量为的小物块,与弹簧间不拴接,开始时处于静止状态。现有另一个质量为的小物块从斜面上某处由静止释放,与发生正碰后立即粘在一起成为组合体。已知弹簧的弹性势能与其形变量的关系为,重力加速度为,弹簧始终未超出弹性限度。下列说法正确的是( )
A.被弹簧反弹后恰好可以回到的释放点
B.整个过程中、和弹簧组成的系统机械能守恒
C.当的释放点到的距离为时,恰好不会与弹簧分离
D.要使能在斜面上做完整的简谐运动,的释放点到的距离至少为
7.如图所示,小球在光滑水平面上以O为平衡位置,在A、B之间做简谐运动,下列说法正确的是( )
A.小球在O点速度最大 B.小球在A点速度最大
C.小球在B点加速度最小 D.小球在B点回复力最小
8.物体产生机械振动的条件是( )
A.有方向不变、大小不变的力作用在物体上
B.有方向不变、大小变化的力作用在物体上
C.有方向变化、大小不变的力作用在物体上
D.有始终指向平衡位置的回复力作用在物体上
9.下列运动中不属于机械振动的是( )
A.树枝在风的作用下运动 B.竖直向上抛出的物体的运动
C.说话时声带的运动 D.爆炸声引起窗扇的运动
10.如图所示,一个劲度系数为k的轻弹簧下端固定在挡板上,上端与物块A连接在一起,物块B紧挨着物块A静止在光滑斜面上。某时刻将B迅速移开,A将在斜面上做简谐运动,已知物块A、B的质量分别为、,若取沿斜面向上为正方向,移开B的时刻为计时起点,则A的振动位移随时间变化的图像是(重力加速度为g)( )
A. B.
C. D.
11.一水平的弹簧振子,以平衡位置O点为中心,在A、B两点间做简谐运动,则( )
A.振子在O点时速度和加速度都达到最大 B.振子的速度减小时,位移增大
C.振子的加速度减小时,速度一定变小 D.振子的速度方向与加速度方向一定相反
12.一个弹簧振子在水平方向做简谐运动,周期为T,则( )
A.若t时刻和时刻振子位移大小相等、方向相同,则一定等于T整数倍
B.若t时刻和时刻振子速度大小相等、方向相反,则一定等于整数倍
C.若,则在t时刻和时刻振子的速度大小一定相等
D.若,则在t时刻和时刻弹簧的长度一定相等
二、填空题
13.如图甲所示为一弹簧振子的振动图像,规定向右的方向为正方向,试根据图像分析以下问题:
(1)如图乙所示的振子振动的起始位置是________,从初始位置开始,振子向________(填“右”或“左”)运动.
(2)在乙图中,找出图像中的O、A、B、C、D各对应振动过程中的位置,即O对应________,A对应________,B对应________,C对应________,D对应________.
(3)在时,振子的速度的方向与时速度的方向_______.
(4)质点在前4s内的位移等于________.
14.男生的声带一般宽而厚,振动_______低,所以声音低沉;女生的声带一般窄而薄,振动_____高,所以声音尖细.说话的嗓门有大有小,这是声音的_______不同.
15.一质点在平衡位置O点附近做简谐运动,它离开O点向着M点运动,0.3s末第一次到达M点,又经过0.2s第二次到达M点,再经过_________s质点将第三次到达M点,若该质点由O出发在4s内通过的路程为20cm,该质点的振幅为_________cm
16.机械振动:物体或者___________在一个位置附近所做的___________运动,叫做机械振动。
17.判断下来说法的正误:
(1)简谐运动是匀变速运动。( )
(2)简谐运动的图像描述的是振动质点的轨迹。( )
三、解答题
18.滑板运动非常有趣。如图所示,某同学踩着滑板在弧形滑道的内壁来回滑行。滑板的这种运动可视为振动吗?若可以,它的平衡位置在哪里?
19.证明:竖直悬挂的弹簧振子的振动是简谐运动.
20.如图所示,A、B质量分别为mA=1kg,mB=2kg,AB间用弹簧连接着,弹簧劲度系数k=100N/m,轻绳一端系在A上,另一端跨过定滑轮,B为套在轻绳上的光滑圆环,另一圆环C固定在桌边,B被C挡住而静止在C上,若开始时作用在绳子另一端的拉力F为零,此时A处于静止且刚没接触地面.现用恒定拉力F=15N拉绳子,恰能使B离开C但不能继续上升,不计摩擦且弹簧没超过弹性限度,求
(1)B刚要离开C时A的加速度,并定性画出A离地面高度h随时间变化的图像.
(2)若把拉力F改为F=30N,则B刚要离开C时,A的加速度和速度.
21.如图所示,一个质量m=1kg的小球装在轻质弹簧的一端,弹簧的另一端固定,该弹簧的劲度系数k=100N/m,小球穿在光滑杆上,能够自由滑动.不加任何外力作用时,小球静止在O点位置.现将小球向右拉至A点,然后由静止释放,小球将做简谐运动,B点是小球向左运动的最远距离.其中OA=10cm,小球运动到A点时弹簧的弹性势能为0.5J,不计其他阻力.求:
(1)小球在B点的位移大小和加速度大小;
(2)小球在振动过程中的最大速度大小.
22.一根弹簧的上端固定,下端系一小球,将小球向下拉一点距离后放手,小球便上下振动起来。试证明这个小球在做简谐运动。(提示:使小球振动的回复力是小球所受到的重力和弹簧弹力的合力)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
A.位移减小时,加速度减小,速度增大。A错误;
B.根据回复力公式可知,位移方向总跟加速度方向相反,跟速度方向可以相同,也可以相反。B错误;
C.物体向平衡位置运动时,速度方向跟位移方向相反,C正确;
D.物体向平衡位置运动时,做加速度减小的加速运动。D错误。
故选C。
2.C
【详解】
A.根据
可知,位移减小时,加速度减小,速度增大,选项A错误;
B.根据
可知,位移方向总跟加速度方向相反,跟速度方向可能相同,也可能相反,选项B错误;
C.物体的运动方向指向平衡位置时,速度方向跟位移方向相反;背向平衡位置时,速度方向跟位移方向相同,选项C正确;
D.水平弹簧振子向平衡位置运动时,加速度方向跟速度方向相同,朝远离平衡位置运动时,加速度方向跟速度方向相反,选项D错误。
故选C。
3.A
【详解】
若从某时刻算起,在半个周期内,振子的速度与开始时等大反向,根据动能定理可知,动能的变化量为零,则合外力的功为零。
故选A。
4.C
【详解】
A.简谐运动的速度是变化的,不可能是匀速直线运动,故A错误;
BCD.简谐运动物体的速度随时间也周期性变化,回复力和加速度随时间作周期性变化,是非匀变速运动,故C正确,BD错误。
故选C。
5.A
【详解】
设PO=h,则
设某时刻弹性绳与竖直方向的夹角为θ,此时球离开O点的距离为x,则弹力的竖直分量
可知合力方向水平,小球将沿直线在A、B之间来回运动;小球受大小为
满足简谐振动的F=-kx的特征,则球的运动是简谐振动;小球经过P点正下方时绳子拉力等于mg。
故选A。
6.C
【详解】
AB.因、碰撞后粘在一起,属于完全非弹性碰撞,整个系统有机械能损失,组合体不可能回到的释放点,故AB错误;
C.静止时,根据平衡条件有
对由机械能守恒定律有
根据动量守恒定律有
从、碰撞结束到向上运动到最高点时弹簧恰好处于原长的过程中,对和弹簧组成的系统由机械能守恒定律有
联立解得
故C正确;
D.要使能在斜面上做完整的简谐运动,能运动到的最高点是弹簧恰好处于原长状态时弹簧顶端所在位置,根据C项中解析可知D错误。
故选C。
7.A
【详解】
由题意小球在光滑水平面上以O为平衡位置,在A、B之间做简谐运动,则O点处小球速度最大,加速度和回复力为零,A、B两点处小球速度为零,加速度和回复力最大。
故选A。
8.D
【详解】
振动需要回复力,回复力应该始终指向平衡位置,故其方向是变化的;回复力大小可以变化,也可以不变化,如果是简谐运动,回复力F=-kx,与位移成正比,不断变化;
故选D。
9.B
【详解】
物体(或物体的某一部分)在某一位置附近的往复运动称为机械振动,树枝的运动、声带的运动以及窗扇的运动均是在其平衡位置附近的振动,只有竖直向上抛出的物体的运动不是在其平衡位置附近的振动。
故选B。
10.B
【详解】
物块A、B紧挨在一起平衡时弹簧压缩量
移走B后,A平衡时弹簧压缩量
因此,负向最大位移为
又时,A在负向最大位移处,故B正确,ACD错误。
故选B。
11.B
【详解】
A.振子通过平衡位置时,速度最大,加速度为零,A错误;
B.振子在平衡位置时速度最大,偏离平衡位置越远速度越小,位移越大,故速度减小时位移增大,B正确;
C.振子在平衡位置时,加速度为零,偏离平衡位置越近加速度越小,速度越大,故加速度减小时速度变大,C错误;
D.振子每次通过同一位置(非最大位移处)时,其加速度方向相同,但速度有两个可能的方向,振子的速度方向与加速度方向可能相同,也可能相反,D错误。
故选B。
12.C
【详解】
A.在t时刻和(t+ t)时刻振子的位移相同,所以这两时刻振子通过同一个位置,而每一个周期内,振子两次出现在同一个位置上,所以当速度方向相同时,则 t可以等于T的整数;当速度方向相反时,则 t不等于T的整数,故A错误;
B.若t时刻和(t+ t)时刻振子运动速度大小相等,方向相反,则 t可能等于的整数倍,也可能大于的整数倍,也可能小于的整数倍,故B错误;
C.若 t=,则在t时刻和(t+ t)时刻振子的位置关于平衡位置对称或经过平衡位置,所以这两时刻速度的大小一定相等,故C正确;
D.若 t=,则在t时刻和(t+ t)时刻振子的位置关于平衡位置对称或经过平衡位置,所以这两时刻位移的大小一定相等,由 知加速度大小一定相等,但弹簧的状态不相同,则长度不相等,故D错误。
故选C。
13. E 右 E G E F E 相反 0
由题中“如图甲所示为一弹簧振子的振动图像”可知,本题考查简谐振动的振动图像,根据简谐振动的振动图像反应的位移与时间的关系.
【详解】
(1)[1]由图知t=0时刻,x=0,说明振子振动的起始位置是E;
[2]t=0时刻位移图像的斜率为正,则振子速度沿正向,即向右;
(2)[3][4][5][6][7]根据位移和起始速度方向可以知道,图像中的O、A、B、C、D各对应振动过程中的位置,即O对应E、A对应G、B对应E、C对应F、D对应E;
(3)[8]在t=2s时,图像的斜率为负,说明振子的速度沿负方向,即向左,t=0速度的方向相反;
(4)[9]质点在前4s内回到了出发点,其位移等于零.
14. 频率 频率 响度
【详解】
[1]男生的声带一般宽而厚,说明声带振动慢,所以频率低;
[2]女生的声带一般窄而薄,说明声带振动快,所以频率高;
[3]响度是声音的三个特征之一,与声音的振幅有关,振幅越大,响度越大,振幅越小,响度越小;题中的“嗓门大小”是说声音的振幅大小,所以声音的响度不同。
此外,声音的另外两个特征分别是音调和音色,音调是指声音的高低,由振动的频率决定;音色反映的是声音的品质与特色,它跟发声体的材料和结构有关。
15. 1.4 2
【详解】
[1]运动过程如图所示,振子第三次通过M点需要经过的时间为;
[2]质点振动周期为,故
解得
16. 物体的一部分 往复
【详解】
[1][2]机械振动:物体或者物体的一部分在一个位置附近所做的往复运动,叫做机械振动。
17. 错 错
【详解】
(1)[1]简谐运动中,回复力随位移的变化而变化,是变力,所以简谐运动是非匀变速运动。故错。
(2)[2]简谐运动的图像描述的是质点的位移随时间变化的规律,不是振动质点的轨迹,故错。
18.可以看成振动;弧形滑道的最低点为平衡位置。
【详解】
可以看成振动,在平衡位置附近的往复运动即为振动,滑板运动在弧形滑道的内壁来回滑行,以弧形滑道的最低点为平衡位置,属于振动。
19.见解析
【详解】
振子处于平衡状态时有
mg=kx0
当振动过程中向下相对平衡位置的位移为x时振子所受的合力为
F=mg-k(x+x0)
联立,可得
F=-kx
符合简谐运动的回复力公式,故为简谐运动。
20.(1)15m/s2,;(2)0,3m/s
【详解】
解:(1)B刚要离开C的时候,弹簧对B的弹力N= mBg,A的受力图如图所示,由牛顿第二定律
mAg+N-F=mAaA
可得
aA==15m/s2
A物体的运动为简谐运动,平衡位置为A所受合力为零的位置,此时弹簧的弹力为5N,弹簧处于压缩,压缩量为0.05m,开始振动时压缩量为,所以振幅L=0.15m。
所以A距离地面高度h随时间t变化的关系式是
h=L-Lcos
则有A离地面高度h随时间变化的图像,如下图所示,
(2)当F=0时,弹簧的伸长量
当F=15N,且A上升到最高点时,弹簧的压缩量
所以A上升的高度
h= x1+ x2=0.3m
A上升过程中
Fh=mAgh+△Ep
所以弹簧弹性势能增加了
△Ep=1.5J
把拉力改为F=30N时,A上升过程中
Fh-mAgh-△Ep=mBv2
解得
v=3m/s
B刚要离开C时,弹簧弹力N= mBg=20N,由牛顿第二定律有
mAg+N-F=mAaA
解得
aA=0
21.(1)0.1m,10 m/s2;(2)1m/s
【详解】
(1)因为振子在做简谐振动,A、B两点关于O点对称.
振子在B点的位移
x=OB=OA=10 cm=0.1m
在B点受力分析可得
FB=kx=ma
解得
a=10 m/s2
(2)振子在O点合力为0,因此在O点速度最大.简谐运动过程中机械能守恒,由A运动到O的过程中,弹性势能转化为动能
可得
解得
v=1m/s
22.见解析
【详解】
设振子的平衡位置为O向下方向为正方向,此时弹簧已经有了一个伸长量h,设弹簧的劲度系数为k由平衡条件得
当振子向下偏离平衡位置的距离为x时,回复力即合外力为
代入得
可见小球所受合外力与它的位移的关系符合简谐运动的特点,这个小球在做简谐运动。
答案第1页,共2页
答案第1页,共2页
