人教版数学九年级下册 27.2.1 相似三角形的判定(第4课时) 课件 (共17张PPT)
文档属性
| 名称 | 人教版数学九年级下册 27.2.1 相似三角形的判定(第4课时) 课件 (共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 11:05:40 | ||
图片预览





文档简介
(共17张PPT)
27.2.1 相似三角形的判定
第4课时
1.理解定理“两角对应相等,两三角形相似”;
2.能灵活地选择定理判定相似三角形.
这两个三角形的三个内角的大小有什么a关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等.
观察你与老师的直角三角尺 , 相似吗?
画一个三角形,使三个角分别为60°,45°, 75° .
①分别量出两个三角形三边的长度;
②这两个三角形相似吗
即:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
一定需三个角对应相等吗?
相似三角形的判别方法:
如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似吗?
C
A
A'
B
B'
C'
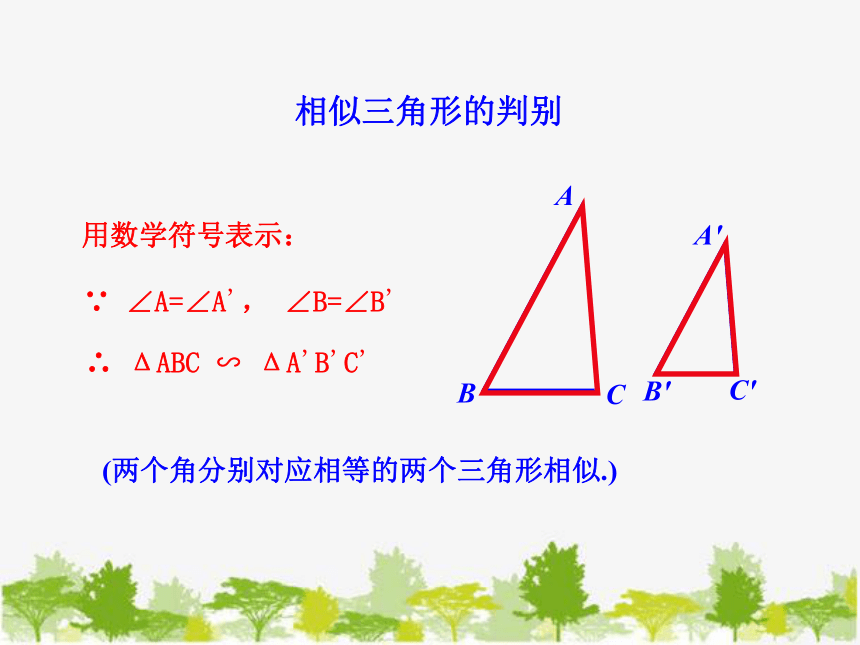
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
用数学符号表示:
相似三角形的判别
(两个角分别对应相等的两个三角形相似.)
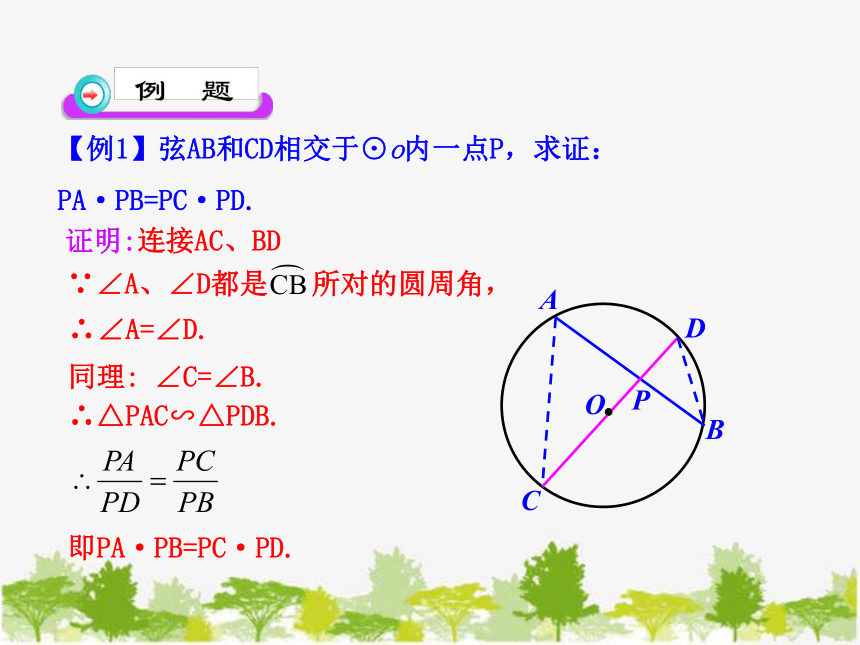
【例1】弦AB和CD相交于⊙o内一点P,求证:
PA·PB=PC·PD.
A
B
C
D
P
O
证明:连接AC、BD
∵∠A、∠D都是 所对的圆周角,
∴∠A=∠D.
同理: ∠C=∠B.
∴△PAC∽△PDB.
即PA·PB=PC·PD.
【例2】如图所示,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,判断这两个三角形是否相似.
C'
B'
A'
C
B
A
解析:∵ ∠B=∠B′=90°(已知),
∠A=∠A′(已知),
∴△ABC∽△A′B′C′(两个角分别对应相等的两个三角形相似.)
A
B
C
E
D
在△ABC 中, D、E 分别是AB、 AC延长线上的点,且 DE∥BC,试说明△ABC与△ADE相似.
解析: ∵ DE∥BC (已知)
∴ ∠AED=∠C(两直线平行,内错角相等),
∵∠EAD=∠CAB.(对顶角)
∴△ADE∽△ABC.
(两组对应角分别相等的两个三角形相似.)
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
O
C
D
A
B
A
B
C
D
E
常见的相似图形
A
B
D
C
图 1
1.填一填
(1)如图1,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC.
(2)如图2,已知:点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似.
A
B
C
E
图 2
ACD
B
(或者∠ACB=∠ADC)
DE//BC
D
(或者∠C=∠AED)
(或者∠B=∠ADE)
2.如图,在□ABCD中,EF∥AB,DE:EA=2:3,EF=4,求CD的长.
解析:∵DE:EA=2:3
∴DE:DA=2:5
∵ EF∥AB
∴△DEF∽△ DAB
∴ DE:DA=EF:AB
2:5=4:AB
AB=10
CD=10
3.如图,△ABC中,DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
A
E
F
B
C
D
解析:∵DE∥BC,EF∥AB(已知),
∴∠ADE=∠B=∠EFC (两直线平行同位角相等)
∠AED=∠C. (两直线平行同位角相等)
∴△ADE∽△EFC. (两个角分别对应相等的两个三角形相似.)
解析: ∵ ∠A= ∠A,∠ABD=∠C
∴ △ABD ∽△ACB
∴ AB :AC=AD :AB
∴ AB2 = AD·AC
∵ AD=2,AC=8
∴ AB =4.
4.已知如图, ∠ABD=∠C,AD=2,AC=8,求AB.
A
B
C
D
解析:(1)△ABC与△FOA相似,因为直线l垂直平分线段AC,所以∠AFO=∠CFO=∠BAC,又∠AOF=∠ABC=90° ,所以△ABC与△FOA相似.
(2)四边形AFCE是菱形,⊿AOE≌⊿COF,所以AE=CF,又AE=CE,AF=CF,所以,AE=CE=AF=CF,所以判定四边形AFCE是菱形.
5.(泰州中考)如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线l分别与线段AD、CB的延长线交于点E、F.
(1)△ABC与△FOA相似吗?为什么?
(2)试判定四边形AFCE的形状,
并说明理由.
相似三角形的判别方法有那些?
方法1:通过定义
方法4:通过两角对应相等.
方法2:平行于三角形一边的直线.
方法3:两边对应成比例且夹角相等.
27.2.1 相似三角形的判定
第4课时
1.理解定理“两角对应相等,两三角形相似”;
2.能灵活地选择定理判定相似三角形.
这两个三角形的三个内角的大小有什么a关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等.
观察你与老师的直角三角尺 , 相似吗?
画一个三角形,使三个角分别为60°,45°, 75° .
①分别量出两个三角形三边的长度;
②这两个三角形相似吗
即:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
一定需三个角对应相等吗?
相似三角形的判别方法:
如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似吗?
C
A
A'
B
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
用数学符号表示:
相似三角形的判别
(两个角分别对应相等的两个三角形相似.)
【例1】弦AB和CD相交于⊙o内一点P,求证:
PA·PB=PC·PD.
A
B
C
D
P
O
证明:连接AC、BD
∵∠A、∠D都是 所对的圆周角,
∴∠A=∠D.
同理: ∠C=∠B.
∴△PAC∽△PDB.
即PA·PB=PC·PD.
【例2】如图所示,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,判断这两个三角形是否相似.
C'
B'
A'
C
B
A
解析:∵ ∠B=∠B′=90°(已知),
∠A=∠A′(已知),
∴△ABC∽△A′B′C′(两个角分别对应相等的两个三角形相似.)
A
B
C
E
D
在△ABC 中, D、E 分别是AB、 AC延长线上的点,且 DE∥BC,试说明△ABC与△ADE相似.
解析: ∵ DE∥BC (已知)
∴ ∠AED=∠C(两直线平行,内错角相等),
∵∠EAD=∠CAB.(对顶角)
∴△ADE∽△ABC.
(两组对应角分别相等的两个三角形相似.)
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
O
C
D
A
B
A
B
C
D
E
常见的相似图形
A
B
D
C
图 1
1.填一填
(1)如图1,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC.
(2)如图2,已知:点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似.
A
B
C
E
图 2
ACD
B
(或者∠ACB=∠ADC)
DE//BC
D
(或者∠C=∠AED)
(或者∠B=∠ADE)
2.如图,在□ABCD中,EF∥AB,DE:EA=2:3,EF=4,求CD的长.
解析:∵DE:EA=2:3
∴DE:DA=2:5
∵ EF∥AB
∴△DEF∽△ DAB
∴ DE:DA=EF:AB
2:5=4:AB
AB=10
CD=10
3.如图,△ABC中,DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
A
E
F
B
C
D
解析:∵DE∥BC,EF∥AB(已知),
∴∠ADE=∠B=∠EFC (两直线平行同位角相等)
∠AED=∠C. (两直线平行同位角相等)
∴△ADE∽△EFC. (两个角分别对应相等的两个三角形相似.)
解析: ∵ ∠A= ∠A,∠ABD=∠C
∴ △ABD ∽△ACB
∴ AB :AC=AD :AB
∴ AB2 = AD·AC
∵ AD=2,AC=8
∴ AB =4.
4.已知如图, ∠ABD=∠C,AD=2,AC=8,求AB.
A
B
C
D
解析:(1)△ABC与△FOA相似,因为直线l垂直平分线段AC,所以∠AFO=∠CFO=∠BAC,又∠AOF=∠ABC=90° ,所以△ABC与△FOA相似.
(2)四边形AFCE是菱形,⊿AOE≌⊿COF,所以AE=CF,又AE=CE,AF=CF,所以,AE=CE=AF=CF,所以判定四边形AFCE是菱形.
5.(泰州中考)如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线l分别与线段AD、CB的延长线交于点E、F.
(1)△ABC与△FOA相似吗?为什么?
(2)试判定四边形AFCE的形状,
并说明理由.
相似三角形的判别方法有那些?
方法1:通过定义
方法4:通过两角对应相等.
方法2:平行于三角形一边的直线.
方法3:两边对应成比例且夹角相等.
