六年级下学期数学6.4数的运算课件(共18张PPT)
文档属性
| 名称 | 六年级下学期数学6.4数的运算课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 175.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-09 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
人教版数学六年级下册 第六单元
数的运算(2)
(教材P77例7-例8)
探究新知
基础练习
拓展练习
课堂小结
复习导入
复习导入
1、四则混合运算的顺序是什么?
先算乘方,再算乘除,最后算加减,同一级运算,一般按从左往右的顺序依次进行,如果有括号,先算括号里面的。
72×165-65×72
2、计算(能简算的要简算)。
2002×
=72×(165-65)
=72×100
=7200
=(2001+1)×
=2001× +1 ×
=2000
=2000
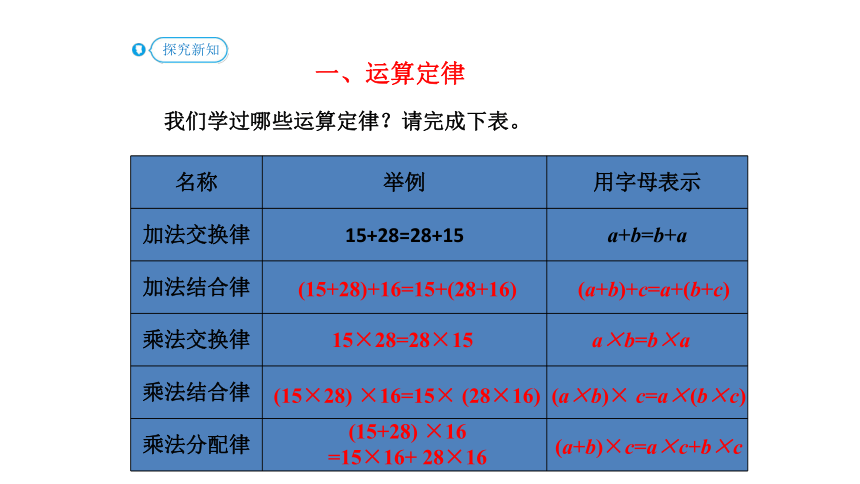
我们学过哪些运算定律?请完成下表。
名称 举例 用字母表示
加法交换律 15+28=28+15 a+b=b+a
加法结合律
乘法交换律
乘法结合律
乘法分配律
(15+28)+16=15+(28+16)
(a+b)+c=a+(b+c)
15×28=28×15
a×b=b×a
(15×28) ×16=15× (28×16)
(a×b)× c=a×(b×c)
(15+28) ×16
=15×16+ 28×16
(a+b)×c=a×c+b×c
探究新知
一、运算定律
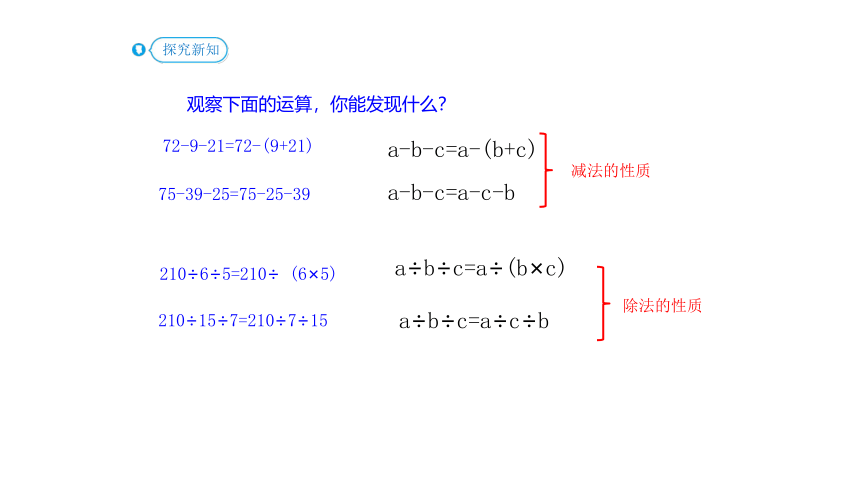
72-9-21=72-(9+21)
75-39-25=75-25-39
210÷6÷5=210÷ (6×5)
210÷15÷7=210÷7÷15
观察下面的运算,你能发现什么?
a-b-c=a-(b+c)
a-b-c=a-c-b
a÷b÷c=a÷(b×c)
a÷b÷c=a÷c÷b
减法的性质
除法的性质
探究新知
1、什么是估算?怎么进行估算?
探究新知
所谓的估算就是大致推算。估算有三种情况:一是推算最大值,二是推算最小值,三是推算大约多少。怎么估算呢?估算都要先对参加计算的数值取其近似值,把一个比较复杂的计算变成可以口算的简单计算,得到一个近似值,如:估算32×58,最大值:都按比原来大的整十数算,最大是40×60=2400;最小值:都按比原来小的整十数算,最小是30×50=1500;约等于多少:用“四舍五入法”取接近的数算,大约在30×60=1800左右。
二、估算
2、 7.99×9.99与80比,哪个大?你是怎么估算的?
80大
3、 比1大吗?你是怎么估算的?
是
二、估算
探究新知
这个估算就 估计它们的最大值,我们可以只将9.99看成10,得数就是79.9,所以应该是80大,也可以把7.99和9.99各看成是8和10,得数是80,但是要考虑到我们都是把原来的数估计大了,所以实际结果应该比80小。
大于,两个相加是1, 和大于的一个数相加,肯定大于1。
(3)妈妈带100元去书店买书,她买了两本文学书,每本20.6元;又花39.6元买了一本汉语词典;之后,妈妈还想买一本家庭菜谱,有两本菜谱可供选择:薄本的13.7元,厚本的23.8元。请帮妈妈估算一下,这时她的钱够买哪一本?
二、估算
探究新知
20.6≈20
39.6≈40
20×2+40=80
100-80=20
20<23.8
所以妈妈只能买薄本的。
4、六年级有五个班,1至5班的人数依次为:43、40、41、44、42,学校小礼堂有200个座位,如果召开六年级毕业典礼,需要加椅子吗?
二、估算
探究新知
你打算怎么估算?
都按40计算,就需要200个,而我们当时估算的时候,都是把原来的数估算小了,所以实际肯定比200大,所以200个椅子肯定是不够的。
5、估算42×29,并和准确结果比一比。
二、估算
探究新知
42≈40
29≈30
40×30=1200
42×29≈1200
42×29=1218
1218-1200=18
估算结果比实际小了18。
一般情况下,我们按四舍五入估算,结果都比较接近准确值,但是如果遇到45×56这种情况,我们将一个数向大估计,一个数向小估计,估算结果比较接近准确值。
6、估算46×55,并和准确结果比一比。
46≈50
55≈60
50×60=3000
46≈50
55≈50
50×50=2500
46×55=2530
相差470
相差30
7、估算713×9,并和准确结果比一比。
二、估算
探究新知
713≈700
9≈10
700×10=7000
713≈700
700×9=6300
713×9=6417
相差583
相差117
像这种一个大数乘一个小数,因为把小数多估算1,估算结果就比实际结果多了一个大数,因此,遇到这样的情况,一般尽量不改变小数,只估算大数,当然,实际情况还要看实际的环境。
二、估算
探究新知
803-207≈ 798+205≈
600
23×498≈ 632÷69≈
1000
10000
10
估算可能有多种结果,这些结果有些和精确值接近一些,但计算速度要慢一些;有些结果没有那么精确,但计算速度要快一些。这些结果在现实生活中都有参考价值。
8、估算
乘法分配律
乘法结合律
4
×
+
×
4
+
=
4
×
(
)
=
4
×
1
4
=
=
34
=
(
0.25
×
4
)
34
×
=
×
1
34
0.25
×
4
×
34
基础练习
1、用简便方法计算,并说一说用了什么定律?
乘法交换律
乘法分配律
乘法结合律
=25×4×125 × 8
=(25×4)×(125 × 8)
=100 ×1000
=100000
25×125×4×8
1.25×(8+10)
=1.25 ×8+1.25 ×10
=10+12.5
=22.5
基础练习
2、用简便方法计算,并说一说过程中用了什么定律?
17.15-8.47-1.53
一个数连续减去两个数,可以用这个数减去这两个数的和。
=17.15—(8.47+1.53)
=17.15—10
=7.15
=4000÷(125×8)
=4000÷1000
=4
一个数连续除以两个数,可以用这个数除以这两个数的积。
4000÷125÷8
1、 计算,并说说是怎样简便运算的?
拓展练习
1. + 估算结果( )。
C
A. 大于1 B. 等于1 C. 小于1
拓展练习
2. 振华小学六(1)班环保小组的5名同学记录了自己家中一周内丢弃塑料袋的数量,结果如下(单位:个):32,25,27,26,25。如果该班有45名同学,根据提供的数据估计本周全班同学全家共丢弃塑料袋大约( )。
A. 900个 B. 1080个 C. 1215个
C
3.体育用品商店开展促销活动,足球销售情况如图所示。
学校需要买10只足球,至少要付( )元钱。
今日足球售价
买1只21元
买2只32元
买3只45元
154
拓展练习
4. 平均每小时有36~45人乘坐游览车,那么3小时中有多少人乘坐游览车?( )
②
①少于100人; ②100~150人之间;
③150~200人之间; ④ 200~250人之间。
拓展练习
①这11个分数的乘积是( );
②这11个分数中,( )与( )的商最大,商是( );( )与( )的积最小,是( )。
1
121
5.先观察下面这组分数的特点,再按要求填空。
、 、 、 、 、 、 、 、 、 、
拓展练习
人教版数学六年级下册 第六单元
数的运算(2)
(教材P77例7-例8)
探究新知
基础练习
拓展练习
课堂小结
复习导入
复习导入
1、四则混合运算的顺序是什么?
先算乘方,再算乘除,最后算加减,同一级运算,一般按从左往右的顺序依次进行,如果有括号,先算括号里面的。
72×165-65×72
2、计算(能简算的要简算)。
2002×
=72×(165-65)
=72×100
=7200
=(2001+1)×
=2001× +1 ×
=2000
=2000
我们学过哪些运算定律?请完成下表。
名称 举例 用字母表示
加法交换律 15+28=28+15 a+b=b+a
加法结合律
乘法交换律
乘法结合律
乘法分配律
(15+28)+16=15+(28+16)
(a+b)+c=a+(b+c)
15×28=28×15
a×b=b×a
(15×28) ×16=15× (28×16)
(a×b)× c=a×(b×c)
(15+28) ×16
=15×16+ 28×16
(a+b)×c=a×c+b×c
探究新知
一、运算定律
72-9-21=72-(9+21)
75-39-25=75-25-39
210÷6÷5=210÷ (6×5)
210÷15÷7=210÷7÷15
观察下面的运算,你能发现什么?
a-b-c=a-(b+c)
a-b-c=a-c-b
a÷b÷c=a÷(b×c)
a÷b÷c=a÷c÷b
减法的性质
除法的性质
探究新知
1、什么是估算?怎么进行估算?
探究新知
所谓的估算就是大致推算。估算有三种情况:一是推算最大值,二是推算最小值,三是推算大约多少。怎么估算呢?估算都要先对参加计算的数值取其近似值,把一个比较复杂的计算变成可以口算的简单计算,得到一个近似值,如:估算32×58,最大值:都按比原来大的整十数算,最大是40×60=2400;最小值:都按比原来小的整十数算,最小是30×50=1500;约等于多少:用“四舍五入法”取接近的数算,大约在30×60=1800左右。
二、估算
2、 7.99×9.99与80比,哪个大?你是怎么估算的?
80大
3、 比1大吗?你是怎么估算的?
是
二、估算
探究新知
这个估算就 估计它们的最大值,我们可以只将9.99看成10,得数就是79.9,所以应该是80大,也可以把7.99和9.99各看成是8和10,得数是80,但是要考虑到我们都是把原来的数估计大了,所以实际结果应该比80小。
大于,两个相加是1, 和大于的一个数相加,肯定大于1。
(3)妈妈带100元去书店买书,她买了两本文学书,每本20.6元;又花39.6元买了一本汉语词典;之后,妈妈还想买一本家庭菜谱,有两本菜谱可供选择:薄本的13.7元,厚本的23.8元。请帮妈妈估算一下,这时她的钱够买哪一本?
二、估算
探究新知
20.6≈20
39.6≈40
20×2+40=80
100-80=20
20<23.8
所以妈妈只能买薄本的。
4、六年级有五个班,1至5班的人数依次为:43、40、41、44、42,学校小礼堂有200个座位,如果召开六年级毕业典礼,需要加椅子吗?
二、估算
探究新知
你打算怎么估算?
都按40计算,就需要200个,而我们当时估算的时候,都是把原来的数估算小了,所以实际肯定比200大,所以200个椅子肯定是不够的。
5、估算42×29,并和准确结果比一比。
二、估算
探究新知
42≈40
29≈30
40×30=1200
42×29≈1200
42×29=1218
1218-1200=18
估算结果比实际小了18。
一般情况下,我们按四舍五入估算,结果都比较接近准确值,但是如果遇到45×56这种情况,我们将一个数向大估计,一个数向小估计,估算结果比较接近准确值。
6、估算46×55,并和准确结果比一比。
46≈50
55≈60
50×60=3000
46≈50
55≈50
50×50=2500
46×55=2530
相差470
相差30
7、估算713×9,并和准确结果比一比。
二、估算
探究新知
713≈700
9≈10
700×10=7000
713≈700
700×9=6300
713×9=6417
相差583
相差117
像这种一个大数乘一个小数,因为把小数多估算1,估算结果就比实际结果多了一个大数,因此,遇到这样的情况,一般尽量不改变小数,只估算大数,当然,实际情况还要看实际的环境。
二、估算
探究新知
803-207≈ 798+205≈
600
23×498≈ 632÷69≈
1000
10000
10
估算可能有多种结果,这些结果有些和精确值接近一些,但计算速度要慢一些;有些结果没有那么精确,但计算速度要快一些。这些结果在现实生活中都有参考价值。
8、估算
乘法分配律
乘法结合律
4
×
+
×
4
+
=
4
×
(
)
=
4
×
1
4
=
=
34
=
(
0.25
×
4
)
34
×
=
×
1
34
0.25
×
4
×
34
基础练习
1、用简便方法计算,并说一说用了什么定律?
乘法交换律
乘法分配律
乘法结合律
=25×4×125 × 8
=(25×4)×(125 × 8)
=100 ×1000
=100000
25×125×4×8
1.25×(8+10)
=1.25 ×8+1.25 ×10
=10+12.5
=22.5
基础练习
2、用简便方法计算,并说一说过程中用了什么定律?
17.15-8.47-1.53
一个数连续减去两个数,可以用这个数减去这两个数的和。
=17.15—(8.47+1.53)
=17.15—10
=7.15
=4000÷(125×8)
=4000÷1000
=4
一个数连续除以两个数,可以用这个数除以这两个数的积。
4000÷125÷8
1、 计算,并说说是怎样简便运算的?
拓展练习
1. + 估算结果( )。
C
A. 大于1 B. 等于1 C. 小于1
拓展练习
2. 振华小学六(1)班环保小组的5名同学记录了自己家中一周内丢弃塑料袋的数量,结果如下(单位:个):32,25,27,26,25。如果该班有45名同学,根据提供的数据估计本周全班同学全家共丢弃塑料袋大约( )。
A. 900个 B. 1080个 C. 1215个
C
3.体育用品商店开展促销活动,足球销售情况如图所示。
学校需要买10只足球,至少要付( )元钱。
今日足球售价
买1只21元
买2只32元
买3只45元
154
拓展练习
4. 平均每小时有36~45人乘坐游览车,那么3小时中有多少人乘坐游览车?( )
②
①少于100人; ②100~150人之间;
③150~200人之间; ④ 200~250人之间。
拓展练习
①这11个分数的乘积是( );
②这11个分数中,( )与( )的商最大,商是( );( )与( )的积最小,是( )。
1
121
5.先观察下面这组分数的特点,再按要求填空。
、 、 、 、 、 、 、 、 、 、
拓展练习
