5.2.2平行线的判定(第2课时) 课件(共26张PPT)
文档属性
| 名称 | 5.2.2平行线的判定(第2课时) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 10:59:56 | ||
图片预览






文档简介
(共26张PPT)
讲授新课
当堂练习
课堂小结
5.2.2 平行线的判定
第2课时 平行线判定方法的综合运用
第五章 相交线与平行线
导入新课
学习目标
1.进一步掌握平行线的判定方法,并会运用平行线的判定解决问题(重点)
2.掌握垂直于同一条直线的两条直线互相平行.(难点)
1.到目前为止,判定两直线平行的方法有哪些?
(1)定义法:(这条不实用)
(2)平行公理的推论:若a//b,b//c,则a//c.
(3)判定方法1:同位角相等,两直线平行.
(4)判定方法2:内错角相等,两直线平行.
(5)判定方法3:同旁内角互补,两直线平行.
导入新课
复习引入
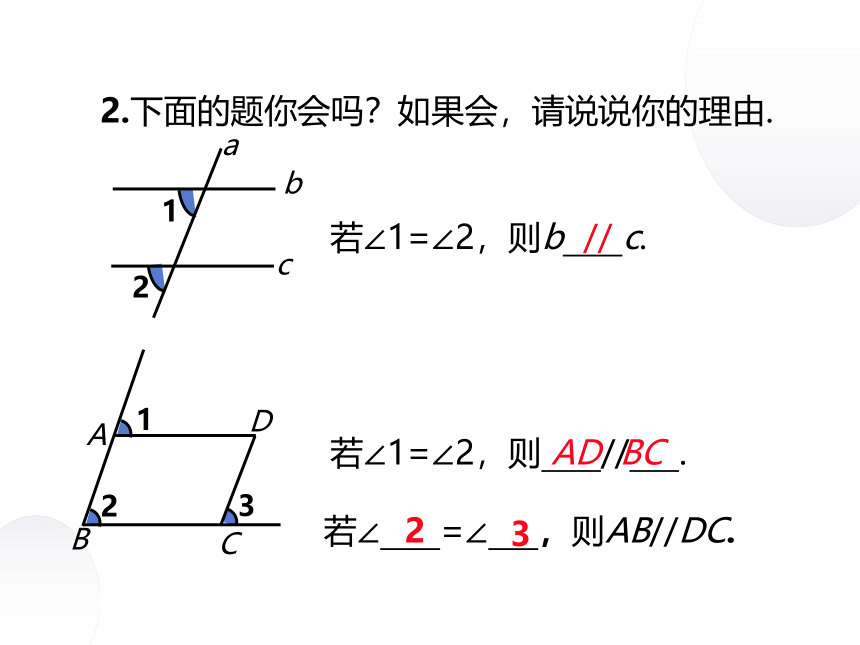
2.下面的题你会吗?如果会,请说说你的理由.
a
b
c
1
2
若∠1=∠2,则b c.
若∠1=∠2,则 // .
若∠ =∠ ,则AB//DC.
C
A
B
D
1
2
3
//
AD
BC
2
3
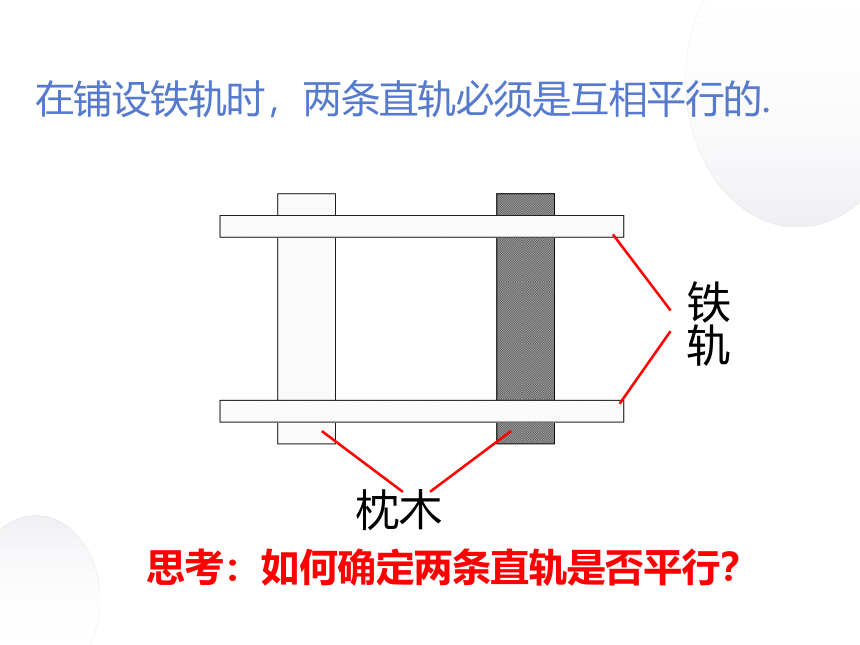
枕木
铁轨
在铺设铁轨时,两条直轨必须是互相平行的.
思考:如何确定两条直轨是否平行?
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?
为什么?
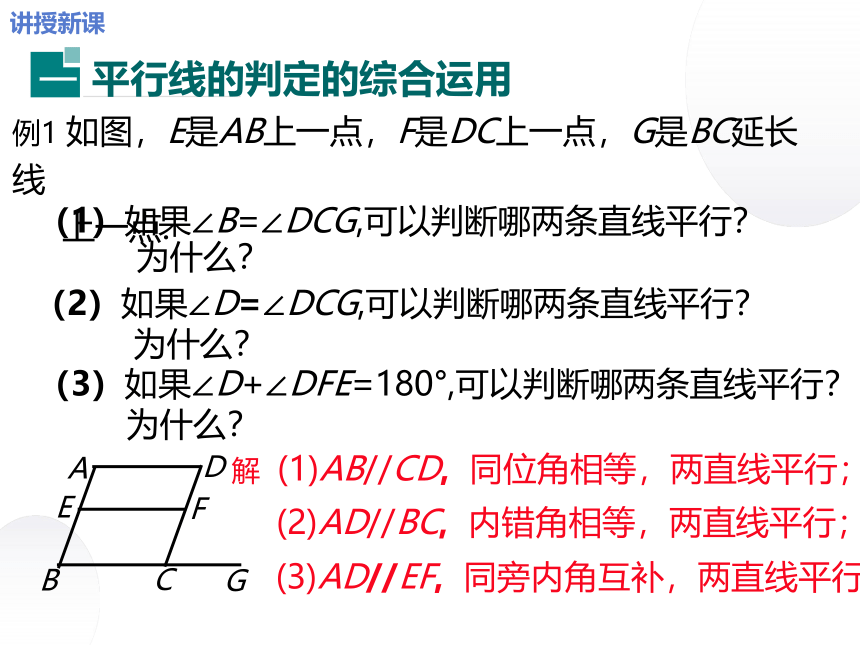
例1 如图,E是AB上一点,F是DC上一点,G是BC延长线
上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行?
为什么?
(2)如果∠D=∠DCG,可以判断哪两条直线平行?
为什么?
A
B
D
C
E
F
G
解 (1)AB//CD, 同位角相等,两直线平行;
(2)AD//BC, 内错角相等,两直线平行;
(3)AD//EF, 同旁内角互补,两直线平行.
讲授新课
平行线的判定的综合运用
一
例2:如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75o
105o
还有其它解法吗?
例2:如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75o
105o
例3 如图,∠1=∠2,能判断AB∥DF吗?为什么?
F
D
C
A
B
E
1
2
解:不能.
添加∠CBD=∠EDB
内错角相等,两直线平行
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由.
思考:在同一平面内,两条直线垂直于同一条直线,
这两条直线平行吗?为什么?
在同一平面内,垂直于同一条直线的两条
直线平行
二
a
b
c
b⊥a,c⊥a
b∥c
?
合作探究
猜想:垂直于同一条直线的两条直线平行.
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
a
b
c
1
2
∵b⊥a ,c ⊥a (已知)
∴b∥c
(同位角相等,两直线平行)
∴∠1= ∠2 = 90°
(垂直的定义)
解法1:如图,
验证猜想
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:如图,
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
2
解法3:如图,
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
同一平面内,垂直于同一条直线
的两条直线平行.
几何语言:
∵ b⊥a,c⊥a(已知)
∴b∥c(同一平面内,垂直于同一条直线的两条
直线平行.)
a
b
c
2
归纳总结
例4 如图,为了说明示意图中的平安大街与长安街
是互相平行的,在地图上量得∠1=90°,你能通过
度量图中已标出的其他的角来验证这个结论吗?
说出你的理由.
解:方法1:测出∠3=90°,
理由是同位角相等,两直线平行.
方法2:测出∠2=90°,
理由是同旁内角互补,两直线平行.
方法3:测出∠5=90°,
理由是内错角相等,两直线平行.
方法4:测出∠2,∠3,∠4,∠5中任意一个角为90°,
理由是同一平面内,垂直于同一直线的两直线平行.
若∠1=120°,∠3=__,即∠1+ ∠3=180°,则AB//CD.
( )
A
B
C
D
E
F
1
2
3
1.如图,直线AB,CD被直线EF所截 .
若∠1=120°,∠2= __ ,则AB//CD.
( )
内错角相等,两直线平行
120°
60°
同旁内角互补,两直线平行
当堂练习
当堂检测
2.用两块相同的三角板按如图所示的方式作平
行线,你能解释其中的道理吗?
解:内错角相等,两直线平行
3.一学员在广场上练习驾驶汽车,两次拐弯后,行驶
方向与原来相同,这两次拐弯的角度可能是( )
A.第一次向右拐50 ,第二次向左拐130
B.第一次向左拐30 ,第二次向右拐30
C.第一次向右拐50 ,第二次向右拐130
D.第一次向左拐50 ,第二次向左拐130
B
3
1
解析:根据平行线的判定定理即可求得答案.
①∵∠B+∠BCD=180°,∴AB∥CD;
②∵∠1=∠2,∴AD∥BC;
③∵∠3=∠4,∴AB∥CD;
④∵∠B=∠5,∴AB∥CD.
∴能得到AB∥CD的条件是①③④.故选C.
4.如图,有以下四个条件:①∠B+∠BCD=180°;
②∠1=∠2;③∠3=∠4;④∠B=∠5.其中能
判定AB∥CD的条件有( )
A.1个 B.2个 C.3个 D.4个
A
B
C
D
E
2
C
5.如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
解:过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ=90°-50°=40°,所以AB∥FQ.
又因为∠1=140°,
所以∠1+∠NFQ=180°,
所以CD∥FQ,所以AB∥CD.
Q
有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?
思维拓展
1
2
方案1:
40°
40°
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
40°
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
1
2
40°
方案2:
140°
40°
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
1
2
方案3:
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.平行于同一直线的两直线平行.
5.同一平面内, 垂直于同一直线的两直线平行.
6.平行线的定义.
判定两条直线是否平行的方法有:
课堂小结
讲授新课
当堂练习
课堂小结
5.2.2 平行线的判定
第2课时 平行线判定方法的综合运用
第五章 相交线与平行线
导入新课
学习目标
1.进一步掌握平行线的判定方法,并会运用平行线的判定解决问题(重点)
2.掌握垂直于同一条直线的两条直线互相平行.(难点)
1.到目前为止,判定两直线平行的方法有哪些?
(1)定义法:(这条不实用)
(2)平行公理的推论:若a//b,b//c,则a//c.
(3)判定方法1:同位角相等,两直线平行.
(4)判定方法2:内错角相等,两直线平行.
(5)判定方法3:同旁内角互补,两直线平行.
导入新课
复习引入
2.下面的题你会吗?如果会,请说说你的理由.
a
b
c
1
2
若∠1=∠2,则b c.
若∠1=∠2,则 // .
若∠ =∠ ,则AB//DC.
C
A
B
D
1
2
3
//
AD
BC
2
3
枕木
铁轨
在铺设铁轨时,两条直轨必须是互相平行的.
思考:如何确定两条直轨是否平行?
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?
为什么?
例1 如图,E是AB上一点,F是DC上一点,G是BC延长线
上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行?
为什么?
(2)如果∠D=∠DCG,可以判断哪两条直线平行?
为什么?
A
B
D
C
E
F
G
解 (1)AB//CD, 同位角相等,两直线平行;
(2)AD//BC, 内错角相等,两直线平行;
(3)AD//EF, 同旁内角互补,两直线平行.
讲授新课
平行线的判定的综合运用
一
例2:如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75o
105o
还有其它解法吗?
例2:如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75o
105o
例3 如图,∠1=∠2,能判断AB∥DF吗?为什么?
F
D
C
A
B
E
1
2
解:不能.
添加∠CBD=∠EDB
内错角相等,两直线平行
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由.
思考:在同一平面内,两条直线垂直于同一条直线,
这两条直线平行吗?为什么?
在同一平面内,垂直于同一条直线的两条
直线平行
二
a
b
c
b⊥a,c⊥a
b∥c
?
合作探究
猜想:垂直于同一条直线的两条直线平行.
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
a
b
c
1
2
∵b⊥a ,c ⊥a (已知)
∴b∥c
(同位角相等,两直线平行)
∴∠1= ∠2 = 90°
(垂直的定义)
解法1:如图,
验证猜想
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:如图,
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
2
解法3:如图,
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
同一平面内,垂直于同一条直线
的两条直线平行.
几何语言:
∵ b⊥a,c⊥a(已知)
∴b∥c(同一平面内,垂直于同一条直线的两条
直线平行.)
a
b
c
2
归纳总结
例4 如图,为了说明示意图中的平安大街与长安街
是互相平行的,在地图上量得∠1=90°,你能通过
度量图中已标出的其他的角来验证这个结论吗?
说出你的理由.
解:方法1:测出∠3=90°,
理由是同位角相等,两直线平行.
方法2:测出∠2=90°,
理由是同旁内角互补,两直线平行.
方法3:测出∠5=90°,
理由是内错角相等,两直线平行.
方法4:测出∠2,∠3,∠4,∠5中任意一个角为90°,
理由是同一平面内,垂直于同一直线的两直线平行.
若∠1=120°,∠3=__,即∠1+ ∠3=180°,则AB//CD.
( )
A
B
C
D
E
F
1
2
3
1.如图,直线AB,CD被直线EF所截 .
若∠1=120°,∠2= __ ,则AB//CD.
( )
内错角相等,两直线平行
120°
60°
同旁内角互补,两直线平行
当堂练习
当堂检测
2.用两块相同的三角板按如图所示的方式作平
行线,你能解释其中的道理吗?
解:内错角相等,两直线平行
3.一学员在广场上练习驾驶汽车,两次拐弯后,行驶
方向与原来相同,这两次拐弯的角度可能是( )
A.第一次向右拐50 ,第二次向左拐130
B.第一次向左拐30 ,第二次向右拐30
C.第一次向右拐50 ,第二次向右拐130
D.第一次向左拐50 ,第二次向左拐130
B
3
1
解析:根据平行线的判定定理即可求得答案.
①∵∠B+∠BCD=180°,∴AB∥CD;
②∵∠1=∠2,∴AD∥BC;
③∵∠3=∠4,∴AB∥CD;
④∵∠B=∠5,∴AB∥CD.
∴能得到AB∥CD的条件是①③④.故选C.
4.如图,有以下四个条件:①∠B+∠BCD=180°;
②∠1=∠2;③∠3=∠4;④∠B=∠5.其中能
判定AB∥CD的条件有( )
A.1个 B.2个 C.3个 D.4个
A
B
C
D
E
2
C
5.如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
解:过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ=90°-50°=40°,所以AB∥FQ.
又因为∠1=140°,
所以∠1+∠NFQ=180°,
所以CD∥FQ,所以AB∥CD.
Q
有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?
思维拓展
1
2
方案1:
40°
40°
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
40°
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
1
2
40°
方案2:
140°
40°
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
1
2
方案3:
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.平行于同一直线的两直线平行.
5.同一平面内, 垂直于同一直线的两直线平行.
6.平行线的定义.
判定两条直线是否平行的方法有:
课堂小结
