青岛版七年级数学下册第13章平面图形的认识 复习课教学设计 (表格式)
文档属性
| 名称 | 青岛版七年级数学下册第13章平面图形的认识 复习课教学设计 (表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 434.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 13:35:17 | ||
图片预览


文档简介
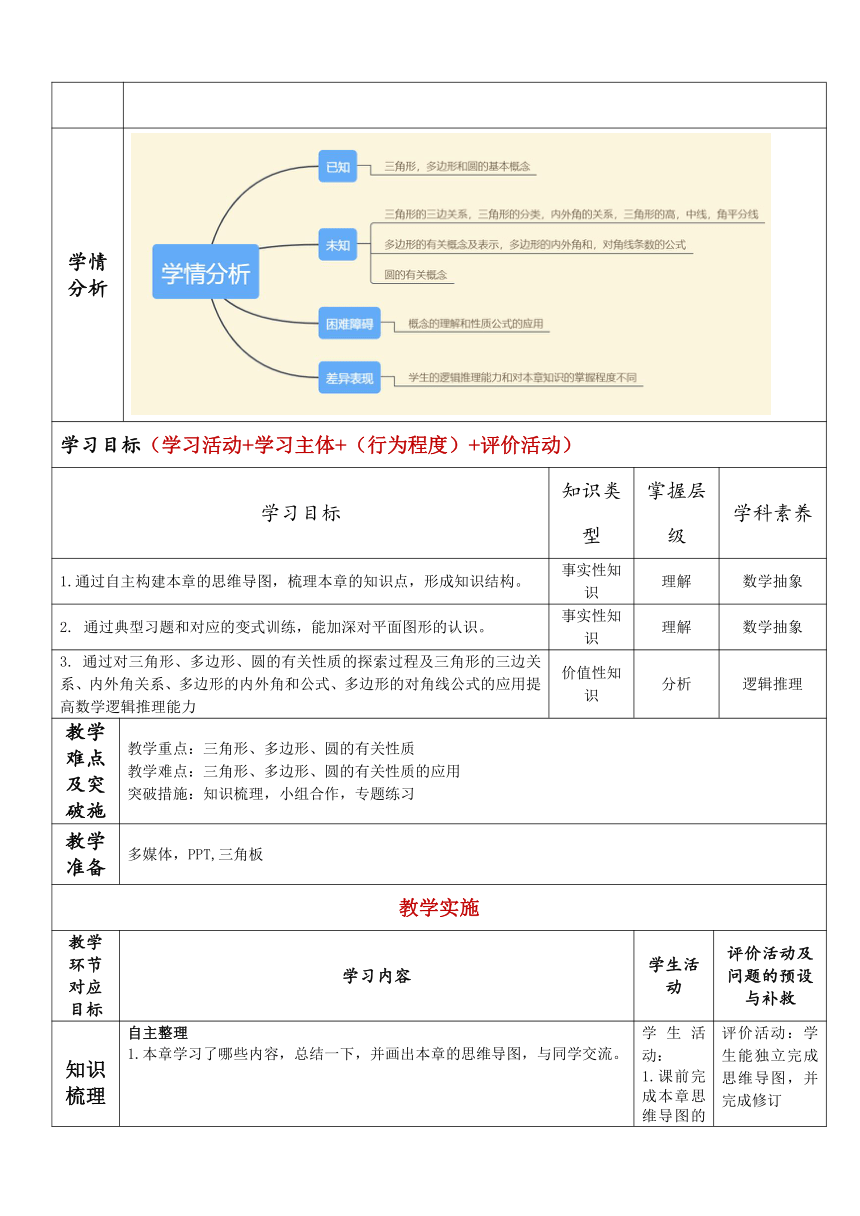
初一数学学程设计
课题 13章平面的基本图形 课型 复习课 序号
学科素养 数学抽象,逻辑推理
课标 分析 通过对三角形、多边形、圆的有关性质的探索过程及三角形的三边关系、内外角关系、多边形的内外角和公式、多边形的对角线公式的应用,会进行简单的有关计算. 通过多边形密铺条件的探索过程,尝试从不同角度解决问题。
教材分析
学情分析
学习目标(学习活动+学习主体+(行为程度)+评价活动)
学习目标 知识类型 掌握层级 学科素养
1.通过自主构建本章的思维导图,梳理本章的知识点,形成知识结构。 事实性知识 理解 数学抽象
2. 通过典型习题和对应的变式训练,能加深对平面图形的认识。 事实性知识 理解 数学抽象
3. 通过对三角形、多边形、圆的有关性质的探索过程及三角形的三边关系、内外角关系、多边形的内外角和公式、多边形的对角线公式的应用提高数学逻辑推理能力 价值性知识 分析 逻辑推理
教学难点及突破施 教学重点:三角形、多边形、圆的有关性质 教学难点:三角形、多边形、圆的有关性质的应用 突破措施:知识梳理,小组合作,专题练习
教学 准备 多媒体,PPT,三角板
教学实施
教学环节对应 目标 学习内容 学生活动 评价活动及 问题的预设与补救
知识梳理 自主整理 1.本章学习了哪些内容,总结一下,并画出本章的思维导图,与同学交流。 学生活动: 1.课前完成本章思维导图的绘制. 2.同学之间交流并相互补充 评价活动:学生能独立完成思维导图,并完成修订
典例解析 典例解析 典例 分析 知识点一:三角形的三边关系
例1 三角形的最长边是10,另两边分别为x和4,周长为c,求x和c的取值范围. 对应练习: 1.有5条线段,长分别为1、2、3、4、5,以其中的三条为边,可以组成 个三角形,它们的边长分别为 . 2.已知,三角形的两边长分别为3和6,则第三边x的取值范围是 . 知识点二:三角形的角平分线和三角形的内角和
例2 如图,△ABC中,BO、CO是角平分线. 若 ∠A=60°,则∠BOC= , 若∠A=90°,则∠BOC= , 若∠A=120°,则∠BOC= , 猜想∠BOC和∠A之间的关系,并证明. 对应练习: 1.若BO为∠ABC的平分线,CO为∠ABC的外角∠ACD的平分线,猜想∠BOC与∠A之间有何关系,请说明理由. 2.若BO、CO分别为外角∠DBC和∠BCE的平分线,猜想∠BOC与∠A之间有何关系,请说明理由.
知识点三:三角形外角的性质 例3.如图,已知∠B=∠CAB,∠ACD=∠D,∠BAD=63°,求∠CAD的度数. 对应练习: 1.求图中∠A+∠B+∠C+∠D+∠E的度数.
2.如图∠B=45°,∠A=30°,∠C=25°,求∠ADC的大小. 知识点四:多边形的性质 例4.(1)若一个多边形的边数增加1,则这个多边形的内角和增加 度.(2)若将n边形的边数增加一倍,则它的内角和增加 度. (3)已知多边形的边数恰好是从一个顶点出发的对角线数的2倍,求此多边形的边数与内角和.
对应练习: 已知八边形的每个内角相等,求每个内角的度数。
2.已知正n边形的每个内角与其外角的差为90°,求边数n.
知识点五:圆的初步认识
例5.如图,AB为⊙O的直径,CD为⊙O的弦,AB、 CD的延长线相交于点E,已知AB=2DE, ∠E=18°,求∠AOC的度数.
对应练习: 1.已知⊙O的半径为10cm,根据下列点P到圆心的距离,判定点P与圆的位置关系,并说明理由.
(1)8cm,(2)10cm,(3)12cm
2.⊙O的半径是3cm,P是⊙O内一点,PO=1cm,则点P到⊙O上各点的最小距离是多少? 学生活动:先独立完成,之后小组讨论,交流答案 学生活动:独立完成,小组交流 学生活动:先独立完成,之后小组讨论,交流答案 学生活动:先独立完成,之后小组讨论,交流答案 学生活动:先独立完成,小组代表展示答案 学生活动:先独立完成,小组代表展示答案 评价活动:学生写出具体的解题过程 问题预设:对最长边这个条件理解不好 突破措施:教师适当点拨,师生共同归纳总结 评价活动:学生能够按照步骤解决问题 问题预设:对应练习1答案不正确,考虑不全 突破措施:做对同学讲解,师生共同归纳总结 评价活动:学生写出具体的解题过程 问题预设:个别学生猜想的证明过程写的不全 突破措施:做的好的同学展示答案,错的同学对照更正 评价活动:学生写出具体的解题过程 问题预设:个别对应练习1的不会做 突破措施:组员互帮,教师点拨 评价活动:学生根据答案自我更正 问题预设:个别同学忘记公式 突破措施:查找课本,再次记忆 评价活动:学生根据答案自我更正 问题预设:个别同学例1没有思路 突破措施:教师适当点拨
达标检测 1. 有两根长为8cm、5cm的木棒,木工师傅要制作一个三角形,如果第三根木棒的长为整数,则第三根木棒的长度有哪几种选法?
2.如图,在直角△ABC中,∠C=90°, AD平分∠BAC,BE平分∠ABC,
则∠APB= 度.
3.求图中∠A+∠B+∠C+∠D+∠E的度数.
4.一个凸多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发地对角线的条数是( )
A.9 B.8 C.7 D.6
5.现有边长相同的正三角形,正方形和正六边形纸片若干张,下列拼法中不能镶嵌成一个平面图案的是( ) A.正方形和正六边形 B.正三角形和正方形 C.正三角形和正六边形 D.正三角形,正方形和正六边形 6.已知⊙ O的周长为10.
(1)若PO=5.5,则点P与圆的位置关系是什么
(2)若PO=4,则点P与圆的位置关系是什么
(3)若PO= ,则点P在圆上. 学生活动:学生在规定时间内独立完成题目,并在小组内订正答案,无法解决的问题进标记. 评价活动:完成题目,并能在小组内解决问题.
能力提升 已知等腰三角形一腰上的高与另一腰的夹角为50°,求这个等腰三角形的底角。 学生活动:先独立完成再小组交流讨论 评价活动: 学生完成题目 问题预设:分类讨论考虑不突破措施:学生代表讲解,教师点拨,学生对照答案更正
作业布置 巩固性作业: 拓展性作业:
板书设计 第13章复习课 思维导图 例题
教学反思 本章的重点是: 三角形、多边形、圆的有关概念。三角形的三边关系、外角的性质,三角形按角或边分类。多边形的内角和公式及外角和公式。 本章的难点是:三角形高的概念、多边形的内角和公式及外角和公式的探索。教学的关键是将数学直观与说理相结合,注意图形语言和符号语言之间的转化。
课题 13章平面的基本图形 课型 复习课 序号
学科素养 数学抽象,逻辑推理
课标 分析 通过对三角形、多边形、圆的有关性质的探索过程及三角形的三边关系、内外角关系、多边形的内外角和公式、多边形的对角线公式的应用,会进行简单的有关计算. 通过多边形密铺条件的探索过程,尝试从不同角度解决问题。
教材分析
学情分析
学习目标(学习活动+学习主体+(行为程度)+评价活动)
学习目标 知识类型 掌握层级 学科素养
1.通过自主构建本章的思维导图,梳理本章的知识点,形成知识结构。 事实性知识 理解 数学抽象
2. 通过典型习题和对应的变式训练,能加深对平面图形的认识。 事实性知识 理解 数学抽象
3. 通过对三角形、多边形、圆的有关性质的探索过程及三角形的三边关系、内外角关系、多边形的内外角和公式、多边形的对角线公式的应用提高数学逻辑推理能力 价值性知识 分析 逻辑推理
教学难点及突破施 教学重点:三角形、多边形、圆的有关性质 教学难点:三角形、多边形、圆的有关性质的应用 突破措施:知识梳理,小组合作,专题练习
教学 准备 多媒体,PPT,三角板
教学实施
教学环节对应 目标 学习内容 学生活动 评价活动及 问题的预设与补救
知识梳理 自主整理 1.本章学习了哪些内容,总结一下,并画出本章的思维导图,与同学交流。 学生活动: 1.课前完成本章思维导图的绘制. 2.同学之间交流并相互补充 评价活动:学生能独立完成思维导图,并完成修订
典例解析 典例解析 典例 分析 知识点一:三角形的三边关系
例1 三角形的最长边是10,另两边分别为x和4,周长为c,求x和c的取值范围. 对应练习: 1.有5条线段,长分别为1、2、3、4、5,以其中的三条为边,可以组成 个三角形,它们的边长分别为 . 2.已知,三角形的两边长分别为3和6,则第三边x的取值范围是 . 知识点二:三角形的角平分线和三角形的内角和
例2 如图,△ABC中,BO、CO是角平分线. 若 ∠A=60°,则∠BOC= , 若∠A=90°,则∠BOC= , 若∠A=120°,则∠BOC= , 猜想∠BOC和∠A之间的关系,并证明. 对应练习: 1.若BO为∠ABC的平分线,CO为∠ABC的外角∠ACD的平分线,猜想∠BOC与∠A之间有何关系,请说明理由. 2.若BO、CO分别为外角∠DBC和∠BCE的平分线,猜想∠BOC与∠A之间有何关系,请说明理由.
知识点三:三角形外角的性质 例3.如图,已知∠B=∠CAB,∠ACD=∠D,∠BAD=63°,求∠CAD的度数. 对应练习: 1.求图中∠A+∠B+∠C+∠D+∠E的度数.
2.如图∠B=45°,∠A=30°,∠C=25°,求∠ADC的大小. 知识点四:多边形的性质 例4.(1)若一个多边形的边数增加1,则这个多边形的内角和增加 度.(2)若将n边形的边数增加一倍,则它的内角和增加 度. (3)已知多边形的边数恰好是从一个顶点出发的对角线数的2倍,求此多边形的边数与内角和.
对应练习: 已知八边形的每个内角相等,求每个内角的度数。
2.已知正n边形的每个内角与其外角的差为90°,求边数n.
知识点五:圆的初步认识
例5.如图,AB为⊙O的直径,CD为⊙O的弦,AB、 CD的延长线相交于点E,已知AB=2DE, ∠E=18°,求∠AOC的度数.
对应练习: 1.已知⊙O的半径为10cm,根据下列点P到圆心的距离,判定点P与圆的位置关系,并说明理由.
(1)8cm,(2)10cm,(3)12cm
2.⊙O的半径是3cm,P是⊙O内一点,PO=1cm,则点P到⊙O上各点的最小距离是多少? 学生活动:先独立完成,之后小组讨论,交流答案 学生活动:独立完成,小组交流 学生活动:先独立完成,之后小组讨论,交流答案 学生活动:先独立完成,之后小组讨论,交流答案 学生活动:先独立完成,小组代表展示答案 学生活动:先独立完成,小组代表展示答案 评价活动:学生写出具体的解题过程 问题预设:对最长边这个条件理解不好 突破措施:教师适当点拨,师生共同归纳总结 评价活动:学生能够按照步骤解决问题 问题预设:对应练习1答案不正确,考虑不全 突破措施:做对同学讲解,师生共同归纳总结 评价活动:学生写出具体的解题过程 问题预设:个别学生猜想的证明过程写的不全 突破措施:做的好的同学展示答案,错的同学对照更正 评价活动:学生写出具体的解题过程 问题预设:个别对应练习1的不会做 突破措施:组员互帮,教师点拨 评价活动:学生根据答案自我更正 问题预设:个别同学忘记公式 突破措施:查找课本,再次记忆 评价活动:学生根据答案自我更正 问题预设:个别同学例1没有思路 突破措施:教师适当点拨
达标检测 1. 有两根长为8cm、5cm的木棒,木工师傅要制作一个三角形,如果第三根木棒的长为整数,则第三根木棒的长度有哪几种选法?
2.如图,在直角△ABC中,∠C=90°, AD平分∠BAC,BE平分∠ABC,
则∠APB= 度.
3.求图中∠A+∠B+∠C+∠D+∠E的度数.
4.一个凸多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发地对角线的条数是( )
A.9 B.8 C.7 D.6
5.现有边长相同的正三角形,正方形和正六边形纸片若干张,下列拼法中不能镶嵌成一个平面图案的是( ) A.正方形和正六边形 B.正三角形和正方形 C.正三角形和正六边形 D.正三角形,正方形和正六边形 6.已知⊙ O的周长为10.
(1)若PO=5.5,则点P与圆的位置关系是什么
(2)若PO=4,则点P与圆的位置关系是什么
(3)若PO= ,则点P在圆上. 学生活动:学生在规定时间内独立完成题目,并在小组内订正答案,无法解决的问题进标记. 评价活动:完成题目,并能在小组内解决问题.
能力提升 已知等腰三角形一腰上的高与另一腰的夹角为50°,求这个等腰三角形的底角。 学生活动:先独立完成再小组交流讨论 评价活动: 学生完成题目 问题预设:分类讨论考虑不突破措施:学生代表讲解,教师点拨,学生对照答案更正
作业布置 巩固性作业: 拓展性作业:
板书设计 第13章复习课 思维导图 例题
教学反思 本章的重点是: 三角形、多边形、圆的有关概念。三角形的三边关系、外角的性质,三角形按角或边分类。多边形的内角和公式及外角和公式。 本章的难点是:三角形高的概念、多边形的内角和公式及外角和公式的探索。教学的关键是将数学直观与说理相结合,注意图形语言和符号语言之间的转化。
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
