江苏省邗江中学(集团)2012-2013学年高二上学期期末考试数学试题(新疆班)
文档属性
| 名称 | 江苏省邗江中学(集团)2012-2013学年高二上学期期末考试数学试题(新疆班) |  | |
| 格式 | zip | ||
| 文件大小 | 204.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-04 14:23:23 | ||
图片预览



文档简介
江苏省邗江中学(集团)2012-2013学年度第一学期
高二数学期终试卷新疆班
第Ⅰ卷(填空题 共70分)
一、填空题(本大题共14小题,每小题5分,共70分)
1、对于命题使得则为 。
2、已知全集集合则 。
3、函数的最小正周期是 。
4、已知,函数,若正实数、满足,则、的大小关系为 。
5、已知向量和的夹角为,,则 。
6、曲线C:在处的切线方程为 。
7、已知是第二象限角,且则 。
8、命题命题是的 条件
(填“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”)。
9、已知扇形的周长为,则该扇形面积的最大值为 。
10、在中,角、、所对的边分别为,若,则角的大小为 。
11、若函数的定义域为则实数的取值范围是 。
12、若函数(a>0且a1)有两个零点,则实数a的取值范围是 。
13、若点O是△ABC所在平面内一点,满足,则的值是 。
14、若关于的方程有四个不同的实数根,则实数的取值范围是 。
第Ⅱ卷(解答题 共90分)
二、解答题(本大题共6小题,共90分. 解答时应写出文字说明、证明过程或演算步骤)
15、(本小题满分14分)
已知函数且函数的最小正周期为
(1)求的值;
(2)若将函数的图像向右平移个单位长度,再将所得到的图像上各点的横坐标伸长到原来的4倍(纵坐标不变),得到函数的图像,求函数的单调递减区间。
16、(本小题满分14分)
已知命题指数函数在上单调递减,命题关于的方程的两个实根均大于3.若“或”为真,“且”为假,求实数的取值范围.
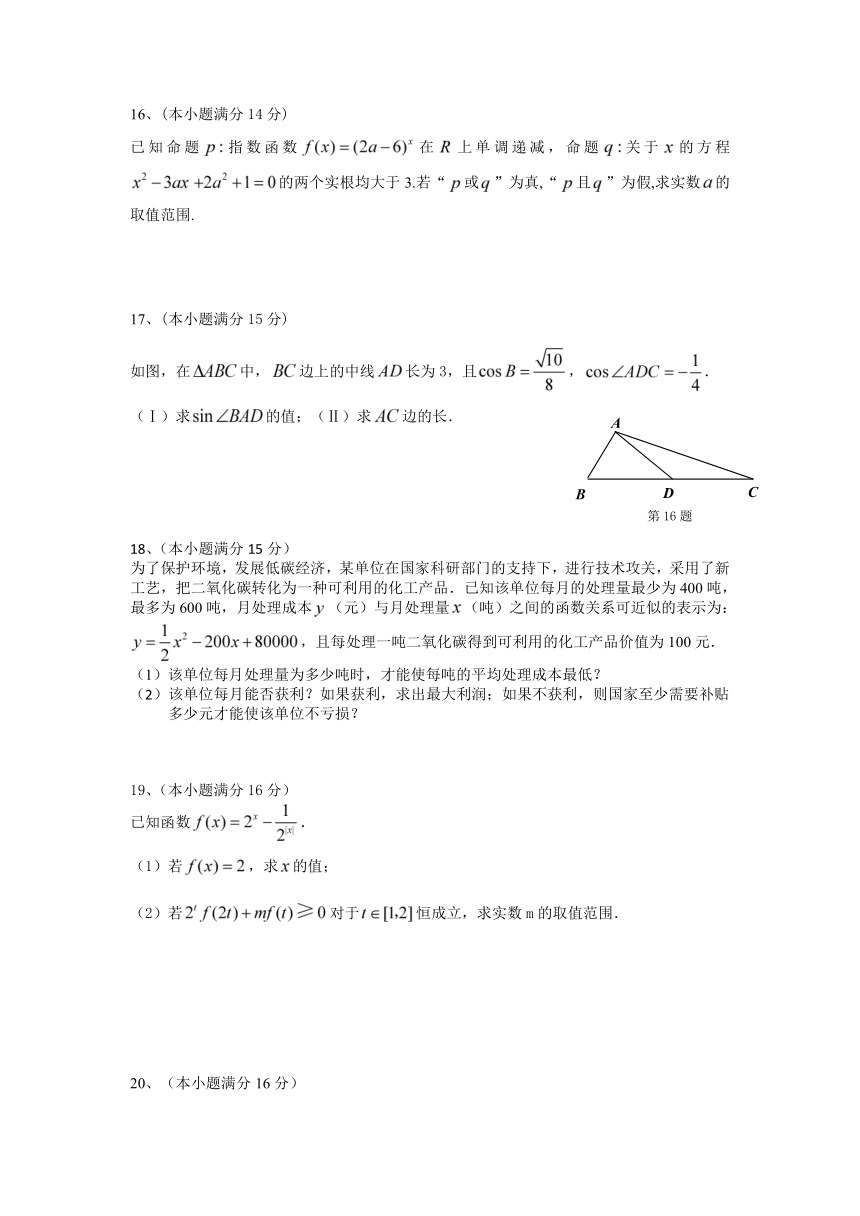
17、(本小题满分15分)
如图,在中,边上的中线长为3,且,.
(Ⅰ)求的值;(Ⅱ)求边的长.
18、(本小题满分15分)
为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本(元)与月处理量(吨)之间的函数关系可近似的表示为:,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
19、(本小题满分16分)
已知函数.
(1)若,求的值;
(2)若对于恒成立,求实数m的取值范围.
20、(本小题满分16分)
已知函数
当a=1时,求函数f(x)的单调增区间
求函数f(x)区间[1,e]上的最小值;
设,若存在,使得成立,求实数a的取值范围。
江苏省邗江中学(集团)2012-2013学年度第一学期
高二数学期终答案
第Ⅰ卷(填空题 共70分)
一、填空题(本大题共14小题,每小题5分,共70分)
1、对于命题使得则为 。,均有≥0;
2、已知全集集合则 。{2}
3、函数的最小正周期是 。
4、已知,函数,若正实数、满足,则、的大小关系为 。m>n
5、已知向量和的夹角为,,则 。
6、曲线C:在处的切线方程为 。y=2x+3
7、已知是第二象限角,且则 。
8、命题命题是的 条件 充分不必要; (填“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”)。
9、已知扇形的周长为,则该扇形面积的最大值为 。
10、在中,角、、所对的边分别为,若,则角的大小为 。
11、若函数的定义域为则实数的取值范围是 。≤m<
12、若函数(a>0且a1)有两个零点,则实数a的取值范围是 。
13、若点O是△ABC所在平面内一点,满足,则的值是 1 :5
14、若关于的方程有四个不同的实数根,则实数的取值范围是 k<-4
第Ⅱ卷(解答题 共90分)
二、解答题(本大题共6小题,共90分. 解答时应写出文字说明、证明过程或演算步骤)
15、(本小题满分14分)
已知函数且函数的最小正周期为
(1)求的值;
(2)若将函数的图像向右平移个单位长度,再将所得到的图像上各点的横坐标伸长到原来的4倍(纵坐标不变),得到函数的图像,求函数的单调递减区间。
16、(本小题满分14分) 已知命题指数函数在上单调递减,命题关于的方程的两个实根均大于3.若“或”为真,“且”为假,求实数的取值范围.
17、(本小题满分15分)
如图,在中,边上的中线长为3,且,.
(Ⅰ)求的值;
(Ⅱ)求边的长.
解:(Ⅰ)因为,所以………………………2分
又,所以…………………………………………… 4分
所以
…………………………………………7分
(Ⅱ)在中,由正弦定理,得,即,解得……10分
故,从而在中,由余弦定理,得
=,所以………………………………14分
18、(本小题满分15分)
为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本(元)与月处理量(吨)之间的函数关系可近似的表示为:,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
解:(1)由题意可知,二氧化碳的每吨平均处理成本为:
…………………………………………………4分
,
当且仅当,即时,
才能使每吨的平均处理成本最低,最低成本为元.…………………8分
(2)设该单位每月获利为,
则…………………………………………………………………10分
因为,所以当时,有最大值.
故该单位不获利,需要国家每月至少补贴元,才能不亏损.…………16分
19、(本小题满分16分)
已知函数.
(1)若,求的值;
(2)若对于恒成立,求实数m的取值范围.
解:(1). …………….2分
由条件可知,解得 …………6分
∵ …………..8分
(2)当 ……………10分
即
………………13分
故m的取值范围是 …………….15分
20、(本小题满分16分)
已知函数
当a=1时,求函数f(x)的单调增区间
求函数f(x)区间[1,e]上的最小值;
设,若存在,使得成立,求实数a的取值范围。
高二数学期终试卷新疆班
第Ⅰ卷(填空题 共70分)
一、填空题(本大题共14小题,每小题5分,共70分)
1、对于命题使得则为 。
2、已知全集集合则 。
3、函数的最小正周期是 。
4、已知,函数,若正实数、满足,则、的大小关系为 。
5、已知向量和的夹角为,,则 。
6、曲线C:在处的切线方程为 。
7、已知是第二象限角,且则 。
8、命题命题是的 条件
(填“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”)。
9、已知扇形的周长为,则该扇形面积的最大值为 。
10、在中,角、、所对的边分别为,若,则角的大小为 。
11、若函数的定义域为则实数的取值范围是 。
12、若函数(a>0且a1)有两个零点,则实数a的取值范围是 。
13、若点O是△ABC所在平面内一点,满足,则的值是 。
14、若关于的方程有四个不同的实数根,则实数的取值范围是 。
第Ⅱ卷(解答题 共90分)
二、解答题(本大题共6小题,共90分. 解答时应写出文字说明、证明过程或演算步骤)
15、(本小题满分14分)
已知函数且函数的最小正周期为
(1)求的值;
(2)若将函数的图像向右平移个单位长度,再将所得到的图像上各点的横坐标伸长到原来的4倍(纵坐标不变),得到函数的图像,求函数的单调递减区间。
16、(本小题满分14分)
已知命题指数函数在上单调递减,命题关于的方程的两个实根均大于3.若“或”为真,“且”为假,求实数的取值范围.
17、(本小题满分15分)
如图,在中,边上的中线长为3,且,.
(Ⅰ)求的值;(Ⅱ)求边的长.
18、(本小题满分15分)
为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本(元)与月处理量(吨)之间的函数关系可近似的表示为:,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
19、(本小题满分16分)
已知函数.
(1)若,求的值;
(2)若对于恒成立,求实数m的取值范围.
20、(本小题满分16分)
已知函数
当a=1时,求函数f(x)的单调增区间
求函数f(x)区间[1,e]上的最小值;
设,若存在,使得成立,求实数a的取值范围。
江苏省邗江中学(集团)2012-2013学年度第一学期
高二数学期终答案
第Ⅰ卷(填空题 共70分)
一、填空题(本大题共14小题,每小题5分,共70分)
1、对于命题使得则为 。,均有≥0;
2、已知全集集合则 。{2}
3、函数的最小正周期是 。
4、已知,函数,若正实数、满足,则、的大小关系为 。m>n
5、已知向量和的夹角为,,则 。
6、曲线C:在处的切线方程为 。y=2x+3
7、已知是第二象限角,且则 。
8、命题命题是的 条件 充分不必要; (填“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”)。
9、已知扇形的周长为,则该扇形面积的最大值为 。
10、在中,角、、所对的边分别为,若,则角的大小为 。
11、若函数的定义域为则实数的取值范围是 。≤m<
12、若函数(a>0且a1)有两个零点,则实数a的取值范围是 。
13、若点O是△ABC所在平面内一点,满足,则的值是 1 :5
14、若关于的方程有四个不同的实数根,则实数的取值范围是 k<-4
第Ⅱ卷(解答题 共90分)
二、解答题(本大题共6小题,共90分. 解答时应写出文字说明、证明过程或演算步骤)
15、(本小题满分14分)
已知函数且函数的最小正周期为
(1)求的值;
(2)若将函数的图像向右平移个单位长度,再将所得到的图像上各点的横坐标伸长到原来的4倍(纵坐标不变),得到函数的图像,求函数的单调递减区间。
16、(本小题满分14分) 已知命题指数函数在上单调递减,命题关于的方程的两个实根均大于3.若“或”为真,“且”为假,求实数的取值范围.
17、(本小题满分15分)
如图,在中,边上的中线长为3,且,.
(Ⅰ)求的值;
(Ⅱ)求边的长.
解:(Ⅰ)因为,所以………………………2分
又,所以…………………………………………… 4分
所以
…………………………………………7分
(Ⅱ)在中,由正弦定理,得,即,解得……10分
故,从而在中,由余弦定理,得
=,所以………………………………14分
18、(本小题满分15分)
为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本(元)与月处理量(吨)之间的函数关系可近似的表示为:,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
解:(1)由题意可知,二氧化碳的每吨平均处理成本为:
…………………………………………………4分
,
当且仅当,即时,
才能使每吨的平均处理成本最低,最低成本为元.…………………8分
(2)设该单位每月获利为,
则…………………………………………………………………10分
因为,所以当时,有最大值.
故该单位不获利,需要国家每月至少补贴元,才能不亏损.…………16分
19、(本小题满分16分)
已知函数.
(1)若,求的值;
(2)若对于恒成立,求实数m的取值范围.
解:(1). …………….2分
由条件可知,解得 …………6分
∵ …………..8分
(2)当 ……………10分
即
………………13分
故m的取值范围是 …………….15分
20、(本小题满分16分)
已知函数
当a=1时,求函数f(x)的单调增区间
求函数f(x)区间[1,e]上的最小值;
设,若存在,使得成立,求实数a的取值范围。
同课章节目录
