天津市天津一中2013届高三上学期第三次月考数学文试题
文档属性
| 名称 | 天津市天津一中2013届高三上学期第三次月考数学文试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 277.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-04 00:00:00 | ||
图片预览



文档简介
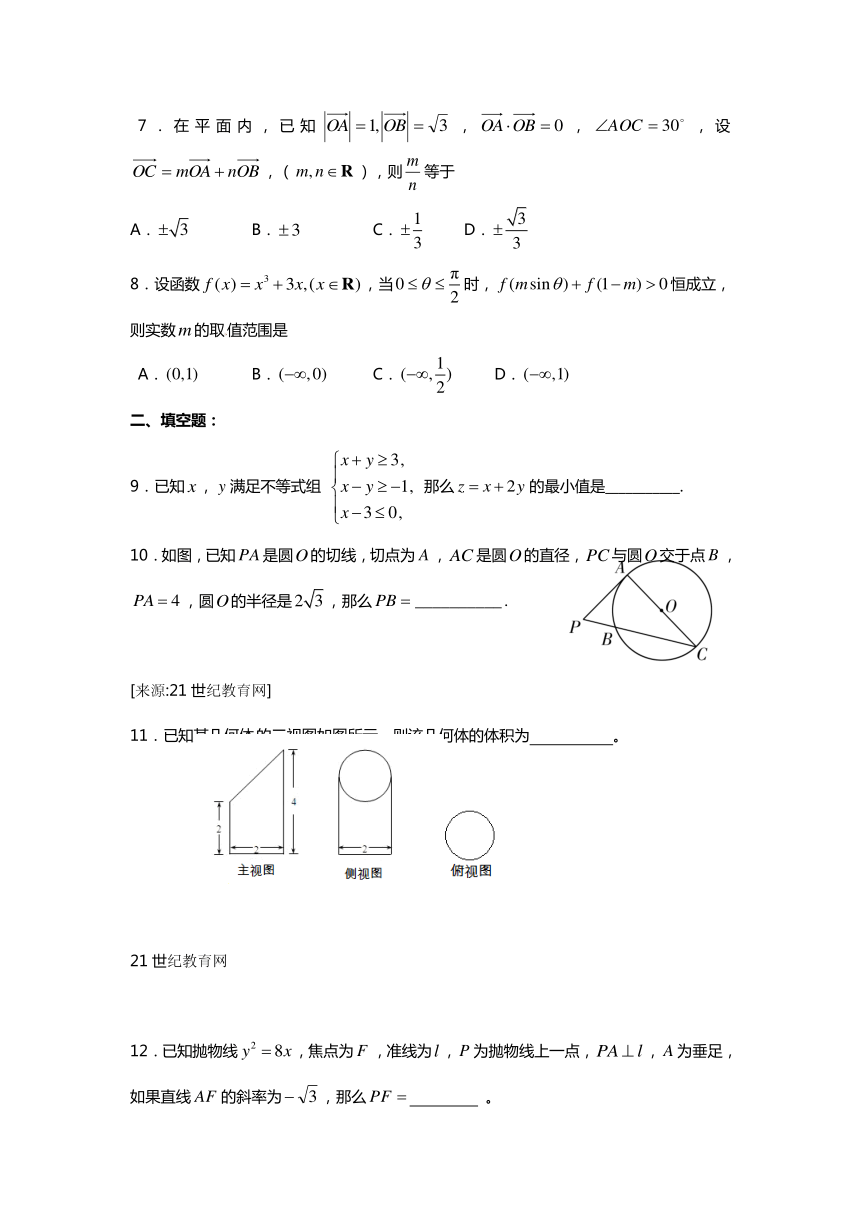
天津一中2012—2013学年高三数学三月考试卷(文科)
一、选择题:
1.复数
A. B. C. D.21世纪教育网2.“ ”是“直线和直线垂直”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.执行右图所示的程序框图,则输出的的值是
A.1 B. C. D.4
4.函数的零点所在的一个区间是
A. B. C. D.
5.设,则
A. B.
C. D.
6.将函数的图像沿轴向右平移个单位,所得图像关于轴对称,则的最小值为
A. B. C. D.
7.在平面内,已知,,,设,(),则等于
A. B. C. D.
8.设函数,当时,恒成立,则实数的取值范围是
A. B. C. D.
二、填空题:
9.已知,满足不等式组 那么的最小值是___________.
10.如图,已知是圆的切线,切点为,是圆的直径,与圆交于点,,圆的半径是,那么
[来源:21世纪教育网]
11.已知某几何体的三视图如图所示,则该几何体的体积为 。
21世纪教育网
12.已知抛物线,焦点为,准线为,为抛物线上一点,,为垂足,如果直线的斜率为,那么 。
13.设集合,,若,则实数取值范围是 。
14.已知函数,若关于的方程有两个不同的实根,则实数的取值范围是_______21世纪教育网
三、解答题:
15.在中,.
(1)求角的大小;_21世纪教育网
(2)若,,求.
16.一个盒子中有5只同型号的灯泡,其中有3只合格品,2只不合格品。现在从中依次取出2只,设每只灯泡被取到的可能性都相同,请用“列举法”解答下列问题:
(1)求第一次取到不合格品,且第二次取到的是合格品的概率;_21世纪教育网
(2)求至少有一次取到不合格品的概率。
17.如图,在四棱锥中,底面是正方形,侧面是正三角形,
且平面⊥底面
(1)求证:⊥平面
(2)求直线与底面所成角的余弦值;
(3)设,求点到平面的距离.
18.已知双曲线的中心在原点,对称轴为坐标轴,一条渐近线方程为,右焦点,双曲线的实轴为,为双曲线上一点(不同于),直线,分别与直线交于两点
(1)求双曲线的方程;
(2)是否为定值,若为定值,求出该值;若不为定值,说明理由。
21世纪教育网
19.已知,点在函数的图象上,其中[来源:21世纪教育网]
(1)求;
(2)证明数列是等比数列;
(3)设,求及数列的通项
21世纪教育网
_21世纪教育网
20.已知函数
(1)如果函数的单调减区间为,求函数的解析式;
(2)在(1)的条件下,求函数的图像过点的切线方程;
(3)证明:对任意的,不等式恒成立,求实数的取值范围。
参考答案
一、选择题:
1-4 AADC 5-8 ACBD
二、填空题:[来源:21世纪教育网]
9.321世纪教育网
10.2
11.
12.8
13.
14.(0,1)
三、解答题:
15.解:(I)由已知得:,……2分
……4分
, …………6分
(II)由 可得: ………7分
…………8分
………10分
解得: ………11分
. ……13分
16.(1) (2)
17.(1)∵底面ABCD是正方形,∴AB⊥AD, ∵平面PAD⊥底面ABCD,AB底面ABCD,底面ABCD∩平面PAD=AD,∴AB⊥平面PAD.
(2)取AD的中点F,连结AF,CF
∵平面PAD⊥平面ABCD,且PF⊥AD,
∴PF⊥平面BCD
∴CF是PC在平面ABCD上的射影,
∴∠PCF是直线PC与底面ABCD所成的角
(3)设点D到平面PBC的距离为h,
在△PBC中,易知PB=PC=
又_21世纪教育网
即点D到平面PBC的距离为21世纪教育网
18.(1)
(2)
21世纪教育网
因为三点共线
,同理
19.解:(1)
(2)由已知,
,两边取对数得
,即
是公比为2的等比数列.
(Ⅱ)由(Ⅰ)知 (*)
=
由(*)式得
20.解:(1)的解集是,所以将代入方程
,
(2)若点是切点,,则切线方程为
若点不是切点,,则切线方程为
(3)在上恒成立
设,
令(舍)
当时,,当时,_21世纪教育网
时,取得最大值,
的取值范围是
同课章节目录
