人教版数学七年级下册第九章 不等式与不等式组9.1.2不等式的性质课件(共21张PPT)
文档属性
| 名称 | 人教版数学七年级下册第九章 不等式与不等式组9.1.2不等式的性质课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 717.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
人教版数学七年级(下)
2016.5.18
温故知新
请你直接说出下列不等式的解集.
(1)x-3>2 (2)2x<6 (3)-x>4
x>5
x<3
x<-4
x>1
探究新知
用“>”、“<”、“=”填空:
(1)5>3,5+2___3+2
(8)5>3,5-2___3-2
(9)a=b,a+3___b+3
(5)a=b,a-5___b-5
(2)a=b,2a___2b
(12)a=b, ___
(4)-1<3,-1+4___3+4
(11)-1<3,-1-3___3-3
(3)6>2,6×5___2×5
(6)6>2,6×(-5)___2×(-5)
(7)-2<4,-2÷2___4÷2
(10)-2<4,-2÷(-2)__4÷(-2)
>
=
>
<
=
<
<
>
=
>
=
<
探究新知
(5)a=b,a-5___b-5
(1)5>3,5+2___3+2
>
(2)a=b,2a___2b
=
(3)6>2,6×5___2×5
>
(4)-1<3,-1+4___3+4
<
=
(6)6>2,6×(-5)___2×(-5)
<
(7)-2<4,-2÷2___4÷2
<
(8)5>3,5-2___3-2
>
(9)a=b,a+3___b+3
=
(10)-2<4,-2÷(-2)___4÷(-2)
>
(12)a=b, ___
=
(11)-1<3,-1-3___3-3
<
(5)a=b,a-5___b-5
=
等式
不等式
探究新知
(5)a=b,a-5___b-5
(2)a=b,2a___2b
=
(9)a=b,a+3___b+3
=
(12)a=b, ___
=
=
等式
等式两边加(或减)同一个数(或式子),结果仍相等.
等式性质1
等式性质2
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
探究新知
(1)5>3,5+2___3+2
>
(3)6>2,6×5___2×5
>
(4)-1<3,-1+4___3+4
<
(6)6>2,6×(-5)___2×(-5)
(7)-2<4,-2÷2___4÷2
<
(8)5>3,5-2___3-2
>
(10)-2<4,-2÷(-2)___4÷(-2)
>
(11)-1<3,-1-3___3-3
<
不等式
等式两边加(或减)同一个数
(或式子),结果仍相等.
等式性质1
等式性质2
等式两边乘同一个数,或除以
同一个不为0的数,结果仍相等.
<
探究新知
(1)5>3,5+2___3+2
>
(3)6>2,6×5___2×5
>
(4)-1<3,-1+4___3+4
<
(7)-2<4,-2÷2___4÷2
<
(8)5>3,5-2___3-2
>
(10)-2<4,-2÷(-2)___4÷(-2)
>
(11)-1<3,-1-3___3-3
<
不等式
(6)6>2,6×(-5)___2×(-5)
<
两边加(减)同一个数
两边乘(除以)同一个数
探究新知
(1)5>3,5+2___3+2
>
(4)-1<3,-1+4___3+4
<
(8)5>3,5-2___3-2
>
(11)-1<3,-1-3___3-3
<
不等式
两边加(减)同一个数
不等式两边加(或减)同一个数,不等号的方向不变.
猜想:
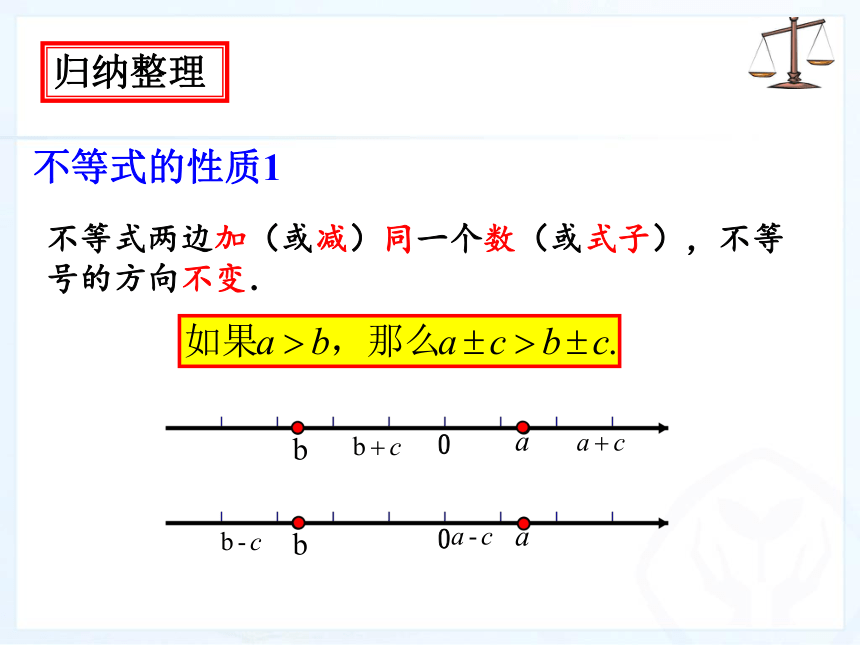
不等式的性质1
0
0
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
归纳整理
两边乘(除以)同一个数
探究新知
(6)6>2,6×(-5)___2×(-5)
<
(10)-2<4,-2÷(-2)___4÷(-2)
>
不等式
(3)6>2,6×5___2×5
>
(7)-2<4,-2÷2___4÷2
<
两边乘(除以)同一个数
探究新知
(6)6>2,6×(-5)___2×(-5)
<
(10)-2<4,-2÷(-2)___4÷(-2)
>
不等式
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式两边乘(或除以)同一个负数,不等号的方向改变.
(3)6>2,6×5___2×5
>
(7)-2<4,-2÷2___4÷2
<
正数
负数
不等号方向不变
不等号方向改变
猜想:
如果a > b,c > 0,那么ac > bc (或 )
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果a > b,c < 0,那么ac < bc (或 )
归纳整理
归纳整理
如果a > b,c > 0,那么ac > bc (或 )
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果a > b,c < 0,那么ac < bc (或 )
不等式的性质1
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
运用新知
方法小结:
看运算 想性质 定方向
√
×
×
×
×
当不等式两边乘或除以一个字母的时候,要对字母进行分类讨论
√
运用新知
例2 利用不等式的性质,解下列不等式:(填空)
(1)x+2>-6,两边都减去2,不等号方向____,得_____;
(2)4x<2,两边都除以4,不等号方向_____,得_____;
不变
x>-8
不变
x<
解不等式就是利用不等式的性质,将不等式进行变形,逐步转化成“x>a”或“x(3)-5x>10,两边都除以-5,不等号方向_____,得_____;
改变
x<-2
请你直接说出下列不等式的解集.
(1)x-3>2 (2)2x<6 (3)-x>4
x>5
x<3
x<-4
x>1
有据可依
(1)- a____- b
(2) 3a+1____3b+1
(3) -2a-3____-2b-3
(4)1-3.5a ___ 1-3.5b
>
<
练习:设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质。
不等式性质3及1
不等式性质3及1
不等式性质2及1
综合运用
不等式性质3
<
<
拓展提高
方法1:
方法2:
一题多解
归纳总结
类比
分类讨论
数形结合
特殊到一般
归 纳
通过本节课的学习你获得了哪些知识和方法?
知识:
1、不等式的性质
不等式的性质1
不等式的性质2
不等式的性质3
不等号的方向
不变
改变
2、不等式的性质运用
看运算 想性质 定方向
乘除遇字母,要对字母分类讨论
方法:
文字语言 符号语言
布置作业
1、作业本:9.1.2 不等式的性质 第一课时
2、选做题:
The End
人教版数学七年级(下)
2016.5.18
温故知新
请你直接说出下列不等式的解集.
(1)x-3>2 (2)2x<6 (3)-x>4
x>5
x<3
x<-4
x>1
探究新知
用“>”、“<”、“=”填空:
(1)5>3,5+2___3+2
(8)5>3,5-2___3-2
(9)a=b,a+3___b+3
(5)a=b,a-5___b-5
(2)a=b,2a___2b
(12)a=b, ___
(4)-1<3,-1+4___3+4
(11)-1<3,-1-3___3-3
(3)6>2,6×5___2×5
(6)6>2,6×(-5)___2×(-5)
(7)-2<4,-2÷2___4÷2
(10)-2<4,-2÷(-2)__4÷(-2)
>
=
>
<
=
<
<
>
=
>
=
<
探究新知
(5)a=b,a-5___b-5
(1)5>3,5+2___3+2
>
(2)a=b,2a___2b
=
(3)6>2,6×5___2×5
>
(4)-1<3,-1+4___3+4
<
=
(6)6>2,6×(-5)___2×(-5)
<
(7)-2<4,-2÷2___4÷2
<
(8)5>3,5-2___3-2
>
(9)a=b,a+3___b+3
=
(10)-2<4,-2÷(-2)___4÷(-2)
>
(12)a=b, ___
=
(11)-1<3,-1-3___3-3
<
(5)a=b,a-5___b-5
=
等式
不等式
探究新知
(5)a=b,a-5___b-5
(2)a=b,2a___2b
=
(9)a=b,a+3___b+3
=
(12)a=b, ___
=
=
等式
等式两边加(或减)同一个数(或式子),结果仍相等.
等式性质1
等式性质2
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
探究新知
(1)5>3,5+2___3+2
>
(3)6>2,6×5___2×5
>
(4)-1<3,-1+4___3+4
<
(6)6>2,6×(-5)___2×(-5)
(7)-2<4,-2÷2___4÷2
<
(8)5>3,5-2___3-2
>
(10)-2<4,-2÷(-2)___4÷(-2)
>
(11)-1<3,-1-3___3-3
<
不等式
等式两边加(或减)同一个数
(或式子),结果仍相等.
等式性质1
等式性质2
等式两边乘同一个数,或除以
同一个不为0的数,结果仍相等.
<
探究新知
(1)5>3,5+2___3+2
>
(3)6>2,6×5___2×5
>
(4)-1<3,-1+4___3+4
<
(7)-2<4,-2÷2___4÷2
<
(8)5>3,5-2___3-2
>
(10)-2<4,-2÷(-2)___4÷(-2)
>
(11)-1<3,-1-3___3-3
<
不等式
(6)6>2,6×(-5)___2×(-5)
<
两边加(减)同一个数
两边乘(除以)同一个数
探究新知
(1)5>3,5+2___3+2
>
(4)-1<3,-1+4___3+4
<
(8)5>3,5-2___3-2
>
(11)-1<3,-1-3___3-3
<
不等式
两边加(减)同一个数
不等式两边加(或减)同一个数,不等号的方向不变.
猜想:
不等式的性质1
0
0
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
归纳整理
两边乘(除以)同一个数
探究新知
(6)6>2,6×(-5)___2×(-5)
<
(10)-2<4,-2÷(-2)___4÷(-2)
>
不等式
(3)6>2,6×5___2×5
>
(7)-2<4,-2÷2___4÷2
<
两边乘(除以)同一个数
探究新知
(6)6>2,6×(-5)___2×(-5)
<
(10)-2<4,-2÷(-2)___4÷(-2)
>
不等式
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式两边乘(或除以)同一个负数,不等号的方向改变.
(3)6>2,6×5___2×5
>
(7)-2<4,-2÷2___4÷2
<
正数
负数
不等号方向不变
不等号方向改变
猜想:
如果a > b,c > 0,那么ac > bc (或 )
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果a > b,c < 0,那么ac < bc (或 )
归纳整理
归纳整理
如果a > b,c > 0,那么ac > bc (或 )
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果a > b,c < 0,那么ac < bc (或 )
不等式的性质1
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
运用新知
方法小结:
看运算 想性质 定方向
√
×
×
×
×
当不等式两边乘或除以一个字母的时候,要对字母进行分类讨论
√
运用新知
例2 利用不等式的性质,解下列不等式:(填空)
(1)x+2>-6,两边都减去2,不等号方向____,得_____;
(2)4x<2,两边都除以4,不等号方向_____,得_____;
不变
x>-8
不变
x<
解不等式就是利用不等式的性质,将不等式进行变形,逐步转化成“x>a”或“x
改变
x<-2
请你直接说出下列不等式的解集.
(1)x-3>2 (2)2x<6 (3)-x>4
x>5
x<3
x<-4
x>1
有据可依
(1)- a____- b
(2) 3a+1____3b+1
(3) -2a-3____-2b-3
(4)1-3.5a ___ 1-3.5b
>
<
练习:设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质。
不等式性质3及1
不等式性质3及1
不等式性质2及1
综合运用
不等式性质3
<
<
拓展提高
方法1:
方法2:
一题多解
归纳总结
类比
分类讨论
数形结合
特殊到一般
归 纳
通过本节课的学习你获得了哪些知识和方法?
知识:
1、不等式的性质
不等式的性质1
不等式的性质2
不等式的性质3
不等号的方向
不变
改变
2、不等式的性质运用
看运算 想性质 定方向
乘除遇字母,要对字母分类讨论
方法:
文字语言 符号语言
布置作业
1、作业本:9.1.2 不等式的性质 第一课时
2、选做题:
The End
