人教版数学七年级下册9.2 一元一次不等式(第3课时)课件(共15张PPT)
文档属性
| 名称 | 人教版数学七年级下册9.2 一元一次不等式(第3课时)课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 21:05:34 | ||
图片预览






文档简介
(共15张PPT)
学习目标:
能从实际问题中抽象出数学问题,根据数量关系建立一元一次不等式进行求解.体会数学建模的思想.
学习重点:
分析实际问题中的不等关系列出一元一次不等式.
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少
本题中,条件是什么?问题是什么?
例3
甲商场优惠方案的起点为购物达 元后;
乙商场优惠方案的起点为购物达 元后.
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少
问题 如果购物款为x元,你能分别表示出在两家商场花费的钱数吗
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少
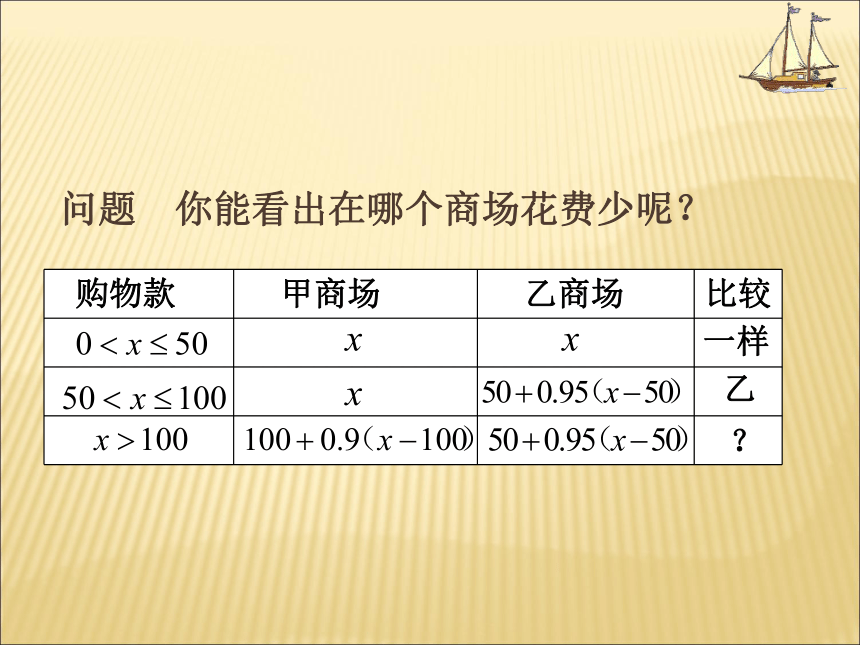
问题 你能看出在哪个商场花费少呢?
购物款 甲商场 乙商场 比较
一样
乙
?
问题 如果累计购物超过100元,在哪家商场花费少呢?
分析:三种情况进行讨论
(1)什么情况下,到甲商场购物花费少?
(2) 什么情况下,到乙商场购物花费少?
(3)什么情况下,两商场花费一样?
(1)若在甲商场花费少,则
.
得 .
(2)若在乙商场花费少,则
.
得 .
(3)若在两商场花费一样,则
.
得 .
综合上面分析,请给出一个合理化的消费方案。
答:购物不超过50元和刚好是150元时,
在两家商场购物没有区别;超过50元而不到150元时在乙商场购物花费少;超过150元后,在甲商场购物花费少.
某种铂金饰品在甲、乙两个商店销售.甲店标价477元/克,按标价出售,不优惠.乙店标价530元/克,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.
(1)若购买铂金饰品的重量为x克,请分别写出到甲、乙商店购买该种所需费:
到甲店购买的费用 ,
到乙店购买的费用 (用含x的式子表示)
(2)李阿姨要买一条重量不少于4克且不超过10克的此种铂金饰品,到哪个商店购买最合算?
1.一元一次不等式的实际问题中最关键是哪一步
2.不等式的实际问题与方程的实际问题有什么相同和不同之处?
小结
教科书 习题9.2 第7、8题
学习目标:
能从实际问题中抽象出数学问题,根据数量关系建立一元一次不等式进行求解.体会数学建模的思想.
学习重点:
分析实际问题中的不等关系列出一元一次不等式.
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少
本题中,条件是什么?问题是什么?
例3
甲商场优惠方案的起点为购物达 元后;
乙商场优惠方案的起点为购物达 元后.
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少
问题 如果购物款为x元,你能分别表示出在两家商场花费的钱数吗
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少
问题 你能看出在哪个商场花费少呢?
购物款 甲商场 乙商场 比较
一样
乙
?
问题 如果累计购物超过100元,在哪家商场花费少呢?
分析:三种情况进行讨论
(1)什么情况下,到甲商场购物花费少?
(2) 什么情况下,到乙商场购物花费少?
(3)什么情况下,两商场花费一样?
(1)若在甲商场花费少,则
.
得 .
(2)若在乙商场花费少,则
.
得 .
(3)若在两商场花费一样,则
.
得 .
综合上面分析,请给出一个合理化的消费方案。
答:购物不超过50元和刚好是150元时,
在两家商场购物没有区别;超过50元而不到150元时在乙商场购物花费少;超过150元后,在甲商场购物花费少.
某种铂金饰品在甲、乙两个商店销售.甲店标价477元/克,按标价出售,不优惠.乙店标价530元/克,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.
(1)若购买铂金饰品的重量为x克,请分别写出到甲、乙商店购买该种所需费:
到甲店购买的费用 ,
到乙店购买的费用 (用含x的式子表示)
(2)李阿姨要买一条重量不少于4克且不超过10克的此种铂金饰品,到哪个商店购买最合算?
1.一元一次不等式的实际问题中最关键是哪一步
2.不等式的实际问题与方程的实际问题有什么相同和不同之处?
小结
教科书 习题9.2 第7、8题
