人教版数学七年级下册 5.2.2 平行线的判定 (共15张PPT)
文档属性
| 名称 | 人教版数学七年级下册 5.2.2 平行线的判定 (共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 21:18:08 | ||
图片预览






文档简介
(共15张PPT)
5.2.2平行线的判定
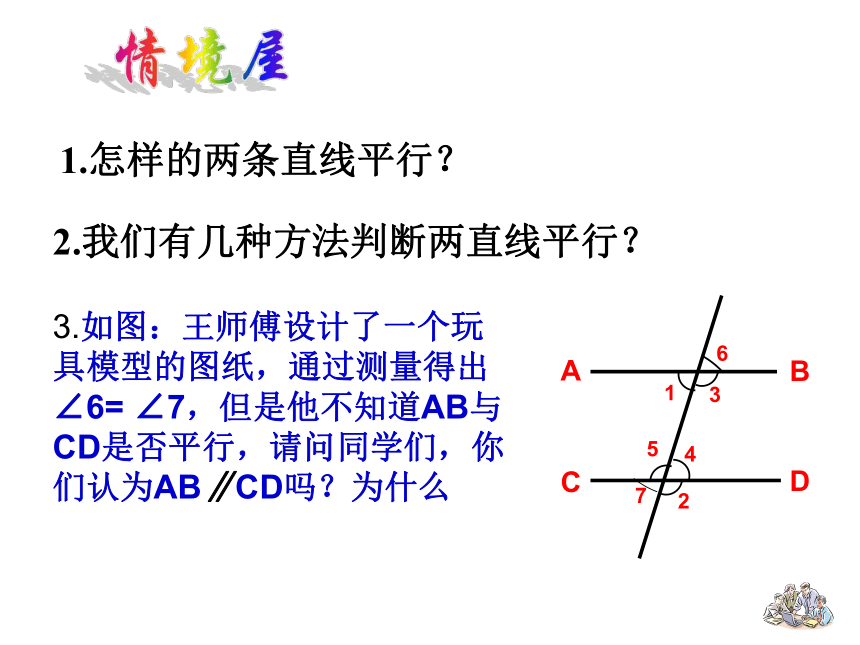
1.怎样的两条直线平行?
2.我们有几种方法判断两直线平行?
3.如图:王师傅设计了一个玩具模型的图纸,通过测量得出∠6= ∠7,但是他不知道AB与CD是否平行,请问同学们,你们认为AB∥CD吗?为什么
A
C
1
4
2
3
B
D
5
6
7
l1
A
2
1
l2
B
(3)请将其最初和最终的特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(1)画图过程中,什么角始终保持相等?
(2)直线l1,l2位置
关系如何?
(4) 由上面,同学们你能发现
判定两直线平行的方法吗?
从画图过程,三角板起到什么作用?
要判断直线a //b,你有办法了吗
c
a
b
1
2
两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:
同位角相等,两直线平行。
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
如图:
大家来探索!
① 如图: 如果∠1=∠2,
那么a与b平行吗?
a
b
l
1
2
3
内错角相等,两直线平行。
∵ ____=____(已知)
∴ ___∥___(内错角相等,两直线平行)
∠1
∠2
a
b
② 如图:
如果∠1+∠2=180o,
那么a与b平行吗?
同旁内角互补,两直线平行。
∵ ____+____=180o(已知)
∴ ___∥___(同旁内角互补,两直线平行)
∠1
∠2
a
b
大家来探索!
a
b
l
1
2
3
4
同位角相等,两直线平行。
同旁内角互补,两直线平行。
内错角相等,两直线平行。
直线平行的判定方法
平行于同一直线的两直线平行。
1.
① ∵ ∠2 =___(已知)
∴ ___∥___
② ∵ ∠3 = ∠5(已知)
∴ ___∥___
③∵ ∠4 +___=180o(已知)
∴ ___∥___
∠6
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
如图:
(同位角相等,两直线平行)
(内错角相等,两直线平行)
(同旁内角互补,两直线平行)
平行线的判定
2.
① ∵ ∠1 =_____(已知)
∴ AB∥CE
② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB
平行线的判定
∠3
∠3
如图:
1
3
5
4
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
3.
如图:王师傅设计了一个玩具模型的图纸,通过测量得出∠6= ∠7,但是他不知道AB与CD是否平行,请问同学们,你们认为AB∥CD吗?为什么?
平行线的判定
A
C
1
4
2
3
B
D
5
6
7
1.火眼金睛,找出图中的平行线
C
A
D
B
E
F
如果∠ADE=∠ABC,则__∥ __
如果∠ACD=∠F, 则__∥ __
如果∠DEC=∠BCF,则__∥ __
DE BC
CD BF
DE BC
2.已知∠3=45°,∠1与∠2互余,试说明AB//CD ?
证明: ∵∠1与∠2互余(已知)
∴ ∠1+∠2=90°(互为余角的定义)
∵∠1=∠2(对顶角相等)
∴∠2+∠2=90°(等量代换)
即∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3(等量代换)
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
想一想
在同一平面内,如果两条直线都垂直于同一直线,那么这两条直线平行吗?为什么?
3.如图:已知,a⊥b,c⊥b, 那么a ∥c吗?为什么?
b
a
c
1
2
学以致用:街道两侧路灯的柱子是否互相平行?为什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
假设今天有老师问你,你们第一节数学课学的什么呀?
判定
数量关系
位置关系
谢谢 大家
5.2.2平行线的判定
1.怎样的两条直线平行?
2.我们有几种方法判断两直线平行?
3.如图:王师傅设计了一个玩具模型的图纸,通过测量得出∠6= ∠7,但是他不知道AB与CD是否平行,请问同学们,你们认为AB∥CD吗?为什么
A
C
1
4
2
3
B
D
5
6
7
l1
A
2
1
l2
B
(3)请将其最初和最终的特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(1)画图过程中,什么角始终保持相等?
(2)直线l1,l2位置
关系如何?
(4) 由上面,同学们你能发现
判定两直线平行的方法吗?
从画图过程,三角板起到什么作用?
要判断直线a //b,你有办法了吗
c
a
b
1
2
两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:
同位角相等,两直线平行。
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
如图:
大家来探索!
① 如图: 如果∠1=∠2,
那么a与b平行吗?
a
b
l
1
2
3
内错角相等,两直线平行。
∵ ____=____(已知)
∴ ___∥___(内错角相等,两直线平行)
∠1
∠2
a
b
② 如图:
如果∠1+∠2=180o,
那么a与b平行吗?
同旁内角互补,两直线平行。
∵ ____+____=180o(已知)
∴ ___∥___(同旁内角互补,两直线平行)
∠1
∠2
a
b
大家来探索!
a
b
l
1
2
3
4
同位角相等,两直线平行。
同旁内角互补,两直线平行。
内错角相等,两直线平行。
直线平行的判定方法
平行于同一直线的两直线平行。
1.
① ∵ ∠2 =___(已知)
∴ ___∥___
② ∵ ∠3 = ∠5(已知)
∴ ___∥___
③∵ ∠4 +___=180o(已知)
∴ ___∥___
∠6
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
如图:
(同位角相等,两直线平行)
(内错角相等,两直线平行)
(同旁内角互补,两直线平行)
平行线的判定
2.
① ∵ ∠1 =_____(已知)
∴ AB∥CE
② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB
平行线的判定
∠3
∠3
如图:
1
3
5
4
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
3.
如图:王师傅设计了一个玩具模型的图纸,通过测量得出∠6= ∠7,但是他不知道AB与CD是否平行,请问同学们,你们认为AB∥CD吗?为什么?
平行线的判定
A
C
1
4
2
3
B
D
5
6
7
1.火眼金睛,找出图中的平行线
C
A
D
B
E
F
如果∠ADE=∠ABC,则__∥ __
如果∠ACD=∠F, 则__∥ __
如果∠DEC=∠BCF,则__∥ __
DE BC
CD BF
DE BC
2.已知∠3=45°,∠1与∠2互余,试说明AB//CD ?
证明: ∵∠1与∠2互余(已知)
∴ ∠1+∠2=90°(互为余角的定义)
∵∠1=∠2(对顶角相等)
∴∠2+∠2=90°(等量代换)
即∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3(等量代换)
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
想一想
在同一平面内,如果两条直线都垂直于同一直线,那么这两条直线平行吗?为什么?
3.如图:已知,a⊥b,c⊥b, 那么a ∥c吗?为什么?
b
a
c
1
2
学以致用:街道两侧路灯的柱子是否互相平行?为什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
假设今天有老师问你,你们第一节数学课学的什么呀?
判定
数量关系
位置关系
谢谢 大家
