青岛版九年级数学下册课件 二次函数复习课课件 (共22张PPT)
文档属性
| 名称 | 青岛版九年级数学下册课件 二次函数复习课课件 (共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 06:47:36 | ||
图片预览






文档简介
(共22张PPT)
二次函数
知识体系的构建
数学家眼里的二次函数:
诗人眼里的二次函数:
同学们眼里的二次函数:
数 图像
优美而舒张的抛物线,犹如人生的轨迹,少年时的努力攀升,力争达到人生的巅峰,但岁月无情的流逝,转而向下
难
二次函数
定义
函数图像与性质
图像的平移
二次函数与一元二次方程的关系
二次函数的应用题
二次函数的综合运用
形如y=ax2+bx+c (a≠0)
(一般式:y=ax2+bx+c (a≠0) )
1.三要素:开口方向、对称轴、顶点坐标
4.a、b、c的作用
2.增减性
3.最值
(顶点式:y=a(x-h)2+k (a≠0) )
待定系数法求函数解析式
1.一般式
2.顶点式
3.交点式
( =0 ; >0 ; <0)
二次函数定义
注意
3. 自变量的最高次数是2。
2. 二次项的系数a≠0。
1. 二次函数解析式必须是整式。
1.下列函数中,是二次函数的是( )
A.y=2x+1 B.y=(x﹣1)2﹣x2
C.y=1﹣x2 D.y=
牛刀小试 :
2、当m为_______时,函数y=(m+1)x - 2x+1 是二次函数?
m+1≠0
=2
C
2
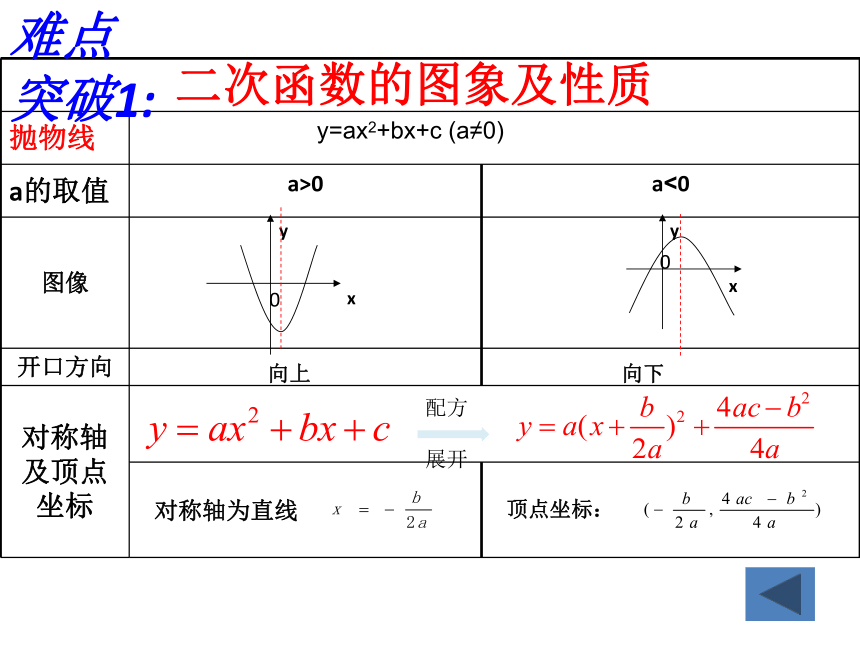
抛物线 y=ax2+bx+c (a≠0) a的取值 a>0 a<0
图像
开口方向
对称轴及顶点坐标
二次函数的图象及性质
对称轴为直线
x
y
x
y
0
0
顶点坐标:
向上
向下
配方
展开
难点
突破1:
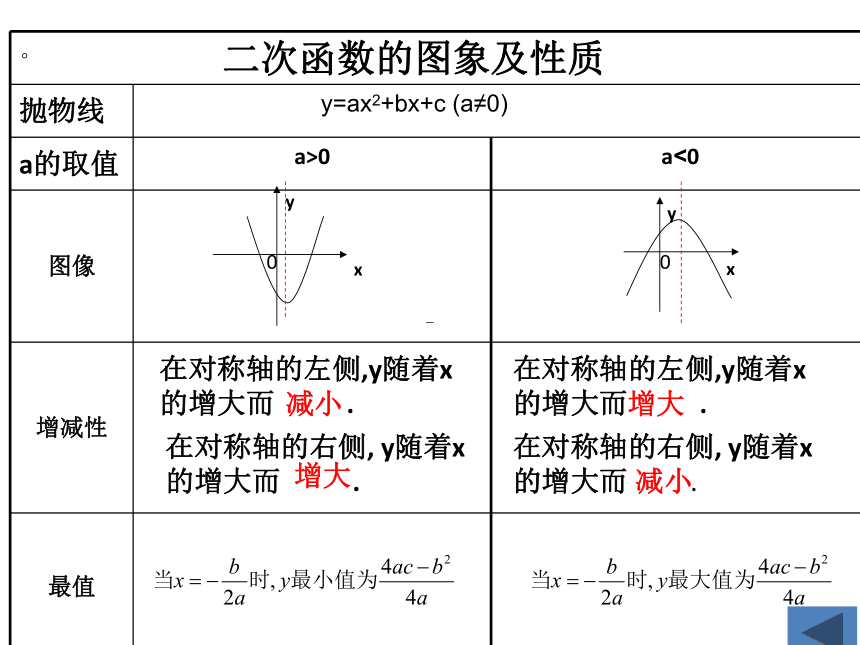
。 抛物线 y=ax2+bx+c (a≠0) a的取值 a>0 a<0
图像
增减性
最值
二次函数的图象及性质
x
y
x
y
0
0
在对称轴的左侧,y随着x的增大而 .
减小
增大
在对称轴的左侧,y随着x的增大而 .
增大
减小
在对称轴的右侧, y随着x的增大而 .
在对称轴的右侧, y随着x
的增大而 .
思考:将抛物线一般式化成顶点式y=a(x-h)2+k (a≠0) ,则对称轴为直线 ,顶点坐标为
x=h
(h,k)
a ﹥0 , x=h时,函数有
最小值
a ﹤ 0 ,x=h时,函数有
最大值
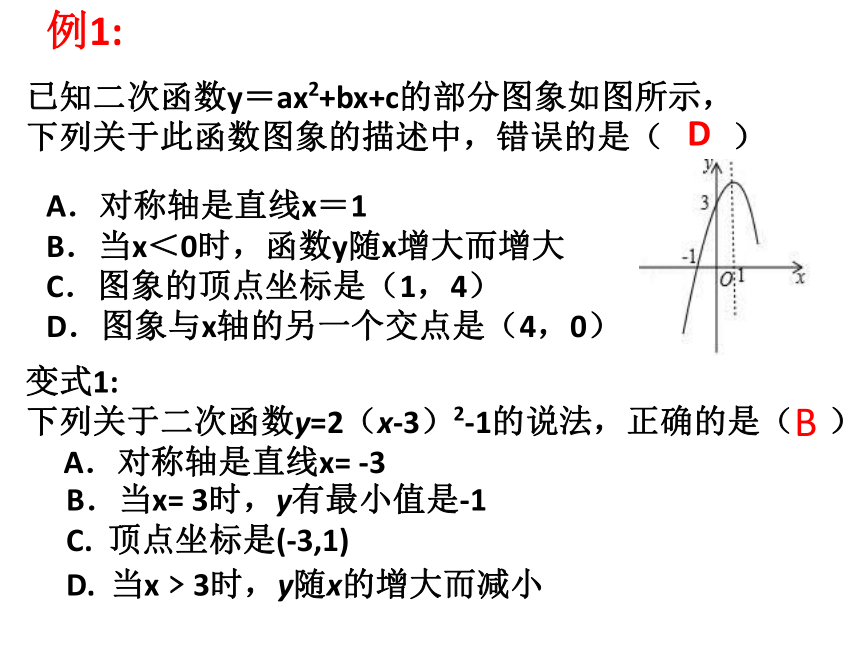
已知二次函数y=ax2+bx+c的部分图象如图所示,
下列关于此函数图象的描述中,错误的是( )
A.对称轴是直线x=1
B.当x<0时,函数y随x增大而增大
C.图象的顶点坐标是(1,4)
D.图象与x轴的另一个交点是(4,0)
例1:
变式1:
下列关于二次函数y=2(x-3)2-1的说法,正确的是( )
A.对称轴是直线x= -3
B.当x= 3时,y有最小值是-1
C. 顶点坐标是(-3,1)
D. 当x﹥3时,y随x的增大而减小
D
B
符号 图像特征
a
b
c
试归纳总结a、b、c的作用
|a|相同
开口方向和开口大 小
相同
不同
(0,c)
左同右异:对称轴在y轴左侧,b 与a符号
对称轴在y轴右侧,b与a 符号
a与b共同决定对称轴的位置
决定抛物线的
两条抛物线开口大小相同
抛物线与y轴的交点坐标
b2-4ac
难点
突破2
二次函数y=ax2+bx+c (a≠0) ,当y=0时,就变成一元二次方程ax2+bx+c =0(a≠0) .
一元二次方程ax2+bx+c (a≠0) 的解是
x
y
0
(1)当 =b2-4ac>0时,方程有两个不相等的实数根,抛物线与x轴有 交点
(2)当 =b2-4ac=0时,方程有两个相等的实数根,抛物线与x轴有 交点
(3)当 =b2-4ac<0时,方程没有实数根,抛物线与x轴 交点
两个
一个
无
抛物线y=ax2+bx+c (a≠0) 的图像与x轴交点的横坐标 。
二次函数与一元二次方程的关系
利用以上知识可以解决:
由抛物线的位置确定系数a , b , c , ⊿等符号及有关a , b , c 的代数式的符号
例2:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+b+c>0,其中正确结论的个数为( ).
A. 4个 B. 3个
C. 2个 D. 1个
o
-1
1 2
x
y
C
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
A.b2<4ac B.ac>0
C.2a﹣b=0 D.a﹣b+c=0
变式 2:
D
y = ax2
y = ax2 + k
y = a(x ± h )2 (h>0)
y = a( x± h )2 + k
上下平移
左右平移
上下平移
左右平移
结论: 一般地,抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同。
二次函数的平移关系
左右平移
谁变呢
上下平移
谁在变?
向左平移,
x+h
向右平移,
x+h
向上平移,k
>0
向下平移,k
<0
思考: 一般地,抛物线 y = a(x-h)2+k与y = ax2有什么联系?
口诀:聚焦顶点,上加下减(y)、左加右减(x)
变式:由二次函数y=x2的图象经过如何平移可以得到函数y=x2-5x+6的图象.
y=x2-5x+6
y=x2
例3
将抛物线y=-5x2 +1 向左平移1个单位长度,再向下平移2个单位长度,所得的抛物线为( )
A. y= -5(x+1)2-1
B.y= -5(x-1)2-1
C. y= -5(x+1)2 +3
D.y= -5(x-1)2 +3
A
二次函数图像的特征与a,b,c的关系
如图,二次函数y=ax2+bx+c的图象与x轴交于点
A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;
②(a+c)2<b2; ③当﹣1<x<3时,y<0;
④当a=1时,将抛物线先向上平移2个单位,再向右平
移1个单位,得到抛物线y=(x﹣2)2﹣2.
其中正确的是( )
A.①③ B.②③
C.②④ D.③④
山东省烟台市2018年中考数学试卷
中考链接:二次函数图像的特征与a,b,c的关系(小组合作探究)
D
巩固练习1:
如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论:①6a﹣b=0; ②abc>0; ③ax2+bx+c≥﹣6;
④若点M(﹣2,m)与点N(﹣5,n)为抛物线上两点,则m>n;
⑤关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1.其中正确结论有( )
A.5
B.4
C.3
D.2
B
待定系数法求函数解析式
一般式:y=ax2+bx+c
顶点式:y=a(x-h)2+k
交点式:y= a(x-x1)(x-x2)
1、已知图像上任意三个点坐标
2、已知图像的顶点(h,k)及另一点
3、已知图像与x轴的两个交点坐标
(x1, 0)(x2, 0)
难点
突破 3
(a≠0)
对称轴为x=
小结:
本节课重要的数学思想方法:
数形结合法
五、当堂达标,反馈矫正
1.若抛物线y=2x2﹣3x﹣k与x轴没有交点,则k的取值范围为_____
2. 已知二次函数y=ax2+bx+c的部分图像如图所示,
对称轴为直线x=-1,则关于x的方程ax2+bx+c=3的
解为__________
3. 关于x的方程ax2+bx+c=0(a≠0)的两个根为 ﹣5和1,则抛物线y=ax2+bx+c(a≠0)的对称轴 是( )
A.x=﹣4 B.x=﹣3 C.x=﹣2 D.x=﹣1
4. 如图为二次函数y=ax2+bx+c的图象,
在下列说法中:①ac<0;
②方程ax2+bx+c=0的根是x1=-1,x2=3;
③a+b+c>0;
④当x>1时,y随着x的增大而增大.
正确的说法有 .(请写出所有正确说法的序号
k<
x=0 或 x =2
C
①②④
通过本节课学习,你收获到了什么?还有那些发面需要提升?
二次函数
知识体系的构建
数学家眼里的二次函数:
诗人眼里的二次函数:
同学们眼里的二次函数:
数 图像
优美而舒张的抛物线,犹如人生的轨迹,少年时的努力攀升,力争达到人生的巅峰,但岁月无情的流逝,转而向下
难
二次函数
定义
函数图像与性质
图像的平移
二次函数与一元二次方程的关系
二次函数的应用题
二次函数的综合运用
形如y=ax2+bx+c (a≠0)
(一般式:y=ax2+bx+c (a≠0) )
1.三要素:开口方向、对称轴、顶点坐标
4.a、b、c的作用
2.增减性
3.最值
(顶点式:y=a(x-h)2+k (a≠0) )
待定系数法求函数解析式
1.一般式
2.顶点式
3.交点式
( =0 ; >0 ; <0)
二次函数定义
注意
3. 自变量的最高次数是2。
2. 二次项的系数a≠0。
1. 二次函数解析式必须是整式。
1.下列函数中,是二次函数的是( )
A.y=2x+1 B.y=(x﹣1)2﹣x2
C.y=1﹣x2 D.y=
牛刀小试 :
2、当m为_______时,函数y=(m+1)x - 2x+1 是二次函数?
m+1≠0
=2
C
2
抛物线 y=ax2+bx+c (a≠0) a的取值 a>0 a<0
图像
开口方向
对称轴及顶点坐标
二次函数的图象及性质
对称轴为直线
x
y
x
y
0
0
顶点坐标:
向上
向下
配方
展开
难点
突破1:
。 抛物线 y=ax2+bx+c (a≠0) a的取值 a>0 a<0
图像
增减性
最值
二次函数的图象及性质
x
y
x
y
0
0
在对称轴的左侧,y随着x的增大而 .
减小
增大
在对称轴的左侧,y随着x的增大而 .
增大
减小
在对称轴的右侧, y随着x的增大而 .
在对称轴的右侧, y随着x
的增大而 .
思考:将抛物线一般式化成顶点式y=a(x-h)2+k (a≠0) ,则对称轴为直线 ,顶点坐标为
x=h
(h,k)
a ﹥0 , x=h时,函数有
最小值
a ﹤ 0 ,x=h时,函数有
最大值
已知二次函数y=ax2+bx+c的部分图象如图所示,
下列关于此函数图象的描述中,错误的是( )
A.对称轴是直线x=1
B.当x<0时,函数y随x增大而增大
C.图象的顶点坐标是(1,4)
D.图象与x轴的另一个交点是(4,0)
例1:
变式1:
下列关于二次函数y=2(x-3)2-1的说法,正确的是( )
A.对称轴是直线x= -3
B.当x= 3时,y有最小值是-1
C. 顶点坐标是(-3,1)
D. 当x﹥3时,y随x的增大而减小
D
B
符号 图像特征
a
b
c
试归纳总结a、b、c的作用
|a|相同
开口方向和开口大 小
相同
不同
(0,c)
左同右异:对称轴在y轴左侧,b 与a符号
对称轴在y轴右侧,b与a 符号
a与b共同决定对称轴的位置
决定抛物线的
两条抛物线开口大小相同
抛物线与y轴的交点坐标
b2-4ac
难点
突破2
二次函数y=ax2+bx+c (a≠0) ,当y=0时,就变成一元二次方程ax2+bx+c =0(a≠0) .
一元二次方程ax2+bx+c (a≠0) 的解是
x
y
0
(1)当 =b2-4ac>0时,方程有两个不相等的实数根,抛物线与x轴有 交点
(2)当 =b2-4ac=0时,方程有两个相等的实数根,抛物线与x轴有 交点
(3)当 =b2-4ac<0时,方程没有实数根,抛物线与x轴 交点
两个
一个
无
抛物线y=ax2+bx+c (a≠0) 的图像与x轴交点的横坐标 。
二次函数与一元二次方程的关系
利用以上知识可以解决:
由抛物线的位置确定系数a , b , c , ⊿等符号及有关a , b , c 的代数式的符号
例2:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+b+c>0,其中正确结论的个数为( ).
A. 4个 B. 3个
C. 2个 D. 1个
o
-1
1 2
x
y
C
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
A.b2<4ac B.ac>0
C.2a﹣b=0 D.a﹣b+c=0
变式 2:
D
y = ax2
y = ax2 + k
y = a(x ± h )2 (h>0)
y = a( x± h )2 + k
上下平移
左右平移
上下平移
左右平移
结论: 一般地,抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同。
二次函数的平移关系
左右平移
谁变呢
上下平移
谁在变?
向左平移,
x+h
向右平移,
x+h
向上平移,k
>0
向下平移,k
<0
思考: 一般地,抛物线 y = a(x-h)2+k与y = ax2有什么联系?
口诀:聚焦顶点,上加下减(y)、左加右减(x)
变式:由二次函数y=x2的图象经过如何平移可以得到函数y=x2-5x+6的图象.
y=x2-5x+6
y=x2
例3
将抛物线y=-5x2 +1 向左平移1个单位长度,再向下平移2个单位长度,所得的抛物线为( )
A. y= -5(x+1)2-1
B.y= -5(x-1)2-1
C. y= -5(x+1)2 +3
D.y= -5(x-1)2 +3
A
二次函数图像的特征与a,b,c的关系
如图,二次函数y=ax2+bx+c的图象与x轴交于点
A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;
②(a+c)2<b2; ③当﹣1<x<3时,y<0;
④当a=1时,将抛物线先向上平移2个单位,再向右平
移1个单位,得到抛物线y=(x﹣2)2﹣2.
其中正确的是( )
A.①③ B.②③
C.②④ D.③④
山东省烟台市2018年中考数学试卷
中考链接:二次函数图像的特征与a,b,c的关系(小组合作探究)
D
巩固练习1:
如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论:①6a﹣b=0; ②abc>0; ③ax2+bx+c≥﹣6;
④若点M(﹣2,m)与点N(﹣5,n)为抛物线上两点,则m>n;
⑤关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1.其中正确结论有( )
A.5
B.4
C.3
D.2
B
待定系数法求函数解析式
一般式:y=ax2+bx+c
顶点式:y=a(x-h)2+k
交点式:y= a(x-x1)(x-x2)
1、已知图像上任意三个点坐标
2、已知图像的顶点(h,k)及另一点
3、已知图像与x轴的两个交点坐标
(x1, 0)(x2, 0)
难点
突破 3
(a≠0)
对称轴为x=
小结:
本节课重要的数学思想方法:
数形结合法
五、当堂达标,反馈矫正
1.若抛物线y=2x2﹣3x﹣k与x轴没有交点,则k的取值范围为_____
2. 已知二次函数y=ax2+bx+c的部分图像如图所示,
对称轴为直线x=-1,则关于x的方程ax2+bx+c=3的
解为__________
3. 关于x的方程ax2+bx+c=0(a≠0)的两个根为 ﹣5和1,则抛物线y=ax2+bx+c(a≠0)的对称轴 是( )
A.x=﹣4 B.x=﹣3 C.x=﹣2 D.x=﹣1
4. 如图为二次函数y=ax2+bx+c的图象,
在下列说法中:①ac<0;
②方程ax2+bx+c=0的根是x1=-1,x2=3;
③a+b+c>0;
④当x>1时,y随着x的增大而增大.
正确的说法有 .(请写出所有正确说法的序号
k<
x=0 或 x =2
C
①②④
通过本节课学习,你收获到了什么?还有那些发面需要提升?
