青岛版九年级数学下册 5.7二次函数的应用(第1课时) 课件 (共20张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 5.7二次函数的应用(第1课时) 课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 603.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 07:02:48 | ||
图片预览






文档简介
(共20张PPT)
5.7二次函数的应用(1)
学科名称:数学
年级:九年级
1.二次函数y=ax2+bx+c(a≠0)何时有最大值或最小值?
2.如何求二次函数的最值?
配方法
公式法
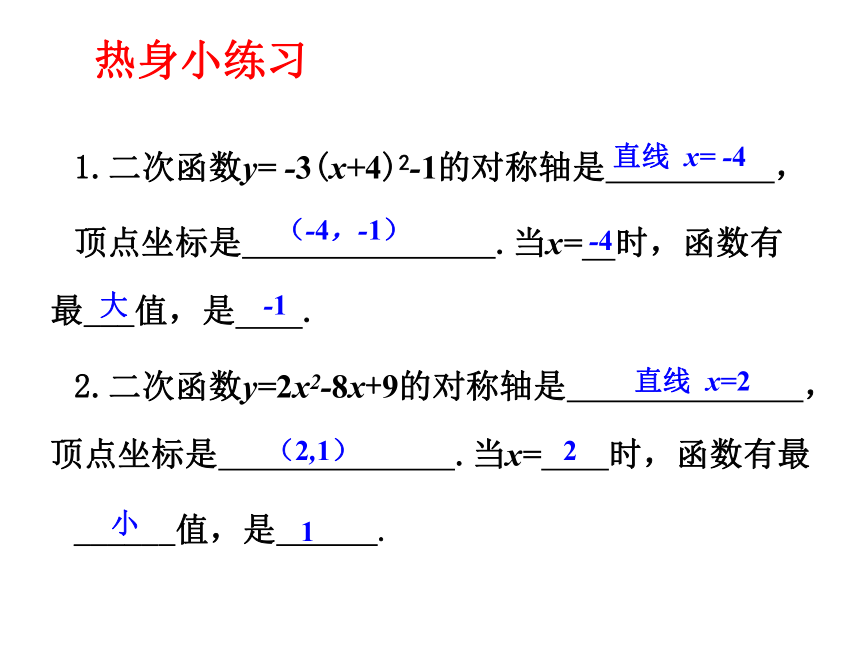
1.二次函数y= -3(x+4)2-1的对称轴是 ,
顶点坐标是 .当x= 时,函数有 最___值,是 .
2.二次函数y=2x2-8x+9的对称轴是 ,顶点坐标是 .当x= 时,函数有最
_____ 值,是 .
直线 x= -4
(-4,-1)
-4
大
-1
直线 x=2
(2,1)
2
小
1
热身小练习
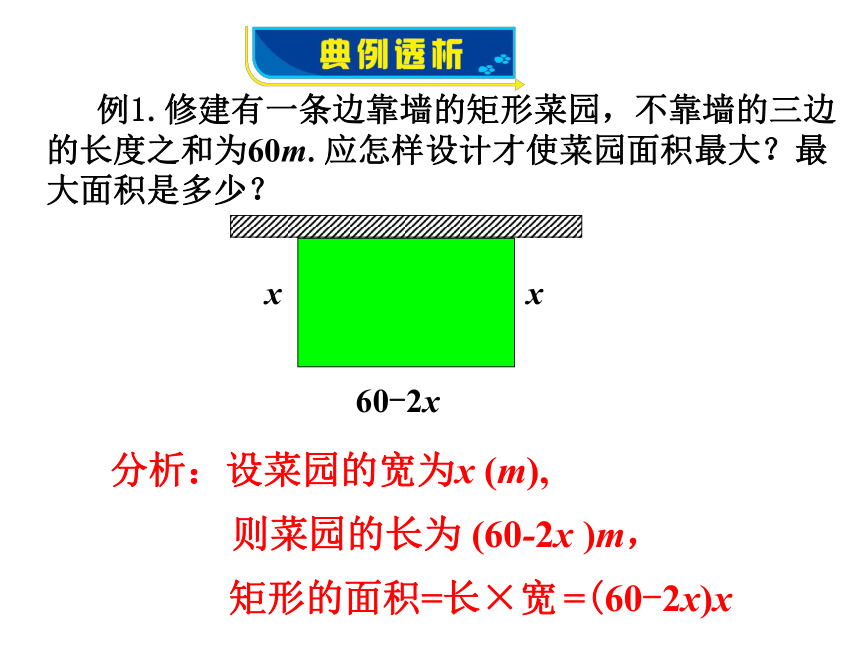
例1.修建有一条边靠墙的矩形菜园,不靠墙的三边的长度之和为60m.应怎样设计才使菜园面积最大?最大面积是多少?
分析:设菜园的宽为x (m),
60-2x
x
x
则菜园的长为 (60-2x )m,
矩形的面积=长×宽
=(60-2x)x
解:如图设菜园的宽为x (m),则菜园的长为 (60-2 x) m, 面积为y (m2),
根据题意,y与x之间的函数解析式为
60-2x
y
x
x
y = x(60-2x)
= -2x2+60x
= -2(x-15)2+450
= -2(x -30x+225-225)
= -2(x -30x)
= -2[(x-15) -225]
∵a= -2<0,所以抛物线开口向下,
∴当x =15时,y有最大值,最大值是450.
又∵自变量的取值范围是: 0<x<30,
∴当菜园的宽为15m时,菜园面积最大,最大面积是450㎡.
一般地,因为抛物线y=ax2+bx+c的顶点是最低(高)点,所以
当 时,二次函数y=ax2+bx+c有最小(大) 值 .
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最大值或最小值.
解决这类题目的一般步骤:
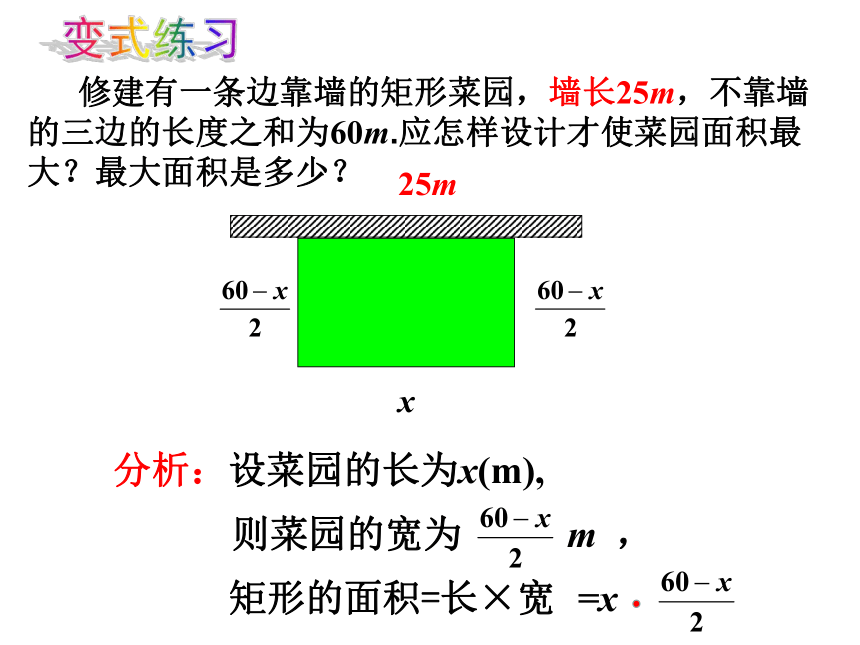
修建有一条边靠墙的矩形菜园,墙长25m,不靠墙的三边的长度之和为60m.应怎样设计才使菜园面积最大?最大面积是多少?
分析:设菜园的长为x(m),
x
则菜园的宽为 m ,
矩形的面积=长×宽
=x
25m
变式练习
解:如图,设菜园的长为x (m),则菜园的宽为 (m),面积为y (m2),
根据题意,y与x之间的函数解析式为
25m
x
y
o
30
450
60
25
例2 如图,ABCD是一块边长为2m的正方形铁板,在边AB上取一点M,分别以AM,MB为边截取两块相邻的正方形板材,当AM的长为多少时,截取的板材面积最小?
分析:截取板材面积=正方形AMPQ面积+正方形MBEF面积.由已知可以构造二次函数,利用二次函数性质解决……
C
2
A
B
D
M
x
Q
P
F
E
解:设AM的长为x(m),则BM的长为(2-x)m,以AM和BM为边的两个正方形面积之和为y(m ).
根据题意,
y与x之间的函数表达式为
y=x +(2-x)
=2x -4x+4
=2(x-1) +2
A
B
C
D
M
x
Q
P
F
E
2
∵a=2>0,抛物线开口向上,
∴x=1时,y有最小值,最小是2.
又 ∵自变量x的取值范围为0<x<2,
∴当AM=1m时,截取的板材面积最小,最小面积是2m .
菱形的两条对角线的和为40cm.
(1)如果菱形的面积为s(cm2),一条对角线的长为x(cm2),写出s与x的函数表达式,并指出自变量x的取值范围;
(2)当这两条对角线的长分别为多少时,菱形的面积最大?最大面积是多少?
变式练习
菱形的两条对角线的和为40cm.
(1) 如果菱形的面积为s(cm2),一条对角线的长为x(cm),写出s与x的函数表达式,并指出自变量x的取值范围;
变式练习
菱形的两条对角线的和为40cm.
(2)当这两条对角线的长分别为多少时,菱形的面积最大?最大面积是多少?
变式练习
.
挑战自我
如图,用篱笆围成一个一面靠墙(墙的最大可用长度为10m)、中间隔着一道篱笆的矩形菜园.已知篱笆的长度为24m.设菜园的宽AB为x(m),面积为y(m ).
(1)写出y与x之间的函数表达式及自变量的取值范围;
(2)围成的菜园的最大面积是多少?这时菜园的宽x等于多少?
A
D
B
C
10
分析:设菜园的宽为x (m),
则菜园的长为(24-3x)m,
矩形的面积=长×宽
=(24-3x)x
x
x
x
24-3x
挑战自我
A
D
B
C
10
解:(1)写出y与x之间的函数表达式及自变量的取值范围;
y=x(24-3x)=3x +24x
∴0<24-3x≤10
x<8
∵ BC≤10,∴24-3x≤10,
x
y
o
4
48
8
挑战自我
∴当x= 时,y最大=
y=x(24-3x)
=3x +24x
= -3(x-4)2+48
(2)围成的菜园的最大面积是多少?这时菜园的宽x等于多少?
所以,围成的菜园的最大面积是 m2,这时菜园的宽x等 于 m.
今天你学到了什么?最深的感受是什么?
实际问题
抽象转化
建立函数模型
数学问题
运用
数学知识
问题的解
返回解释
检验
必做题:习题5.7 3题
选做题:习题5.7 7题
当 堂 作 业 题
5.7二次函数的应用(1)
学科名称:数学
年级:九年级
1.二次函数y=ax2+bx+c(a≠0)何时有最大值或最小值?
2.如何求二次函数的最值?
配方法
公式法
1.二次函数y= -3(x+4)2-1的对称轴是 ,
顶点坐标是 .当x= 时,函数有 最___值,是 .
2.二次函数y=2x2-8x+9的对称轴是 ,顶点坐标是 .当x= 时,函数有最
_____ 值,是 .
直线 x= -4
(-4,-1)
-4
大
-1
直线 x=2
(2,1)
2
小
1
热身小练习
例1.修建有一条边靠墙的矩形菜园,不靠墙的三边的长度之和为60m.应怎样设计才使菜园面积最大?最大面积是多少?
分析:设菜园的宽为x (m),
60-2x
x
x
则菜园的长为 (60-2x )m,
矩形的面积=长×宽
=(60-2x)x
解:如图设菜园的宽为x (m),则菜园的长为 (60-2 x) m, 面积为y (m2),
根据题意,y与x之间的函数解析式为
60-2x
y
x
x
y = x(60-2x)
= -2x2+60x
= -2(x-15)2+450
= -2(x -30x+225-225)
= -2(x -30x)
= -2[(x-15) -225]
∵a= -2<0,所以抛物线开口向下,
∴当x =15时,y有最大值,最大值是450.
又∵自变量的取值范围是: 0<x<30,
∴当菜园的宽为15m时,菜园面积最大,最大面积是450㎡.
一般地,因为抛物线y=ax2+bx+c的顶点是最低(高)点,所以
当 时,二次函数y=ax2+bx+c有最小(大) 值 .
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最大值或最小值.
解决这类题目的一般步骤:
修建有一条边靠墙的矩形菜园,墙长25m,不靠墙的三边的长度之和为60m.应怎样设计才使菜园面积最大?最大面积是多少?
分析:设菜园的长为x(m),
x
则菜园的宽为 m ,
矩形的面积=长×宽
=x
25m
变式练习
解:如图,设菜园的长为x (m),则菜园的宽为 (m),面积为y (m2),
根据题意,y与x之间的函数解析式为
25m
x
y
o
30
450
60
25
例2 如图,ABCD是一块边长为2m的正方形铁板,在边AB上取一点M,分别以AM,MB为边截取两块相邻的正方形板材,当AM的长为多少时,截取的板材面积最小?
分析:截取板材面积=正方形AMPQ面积+正方形MBEF面积.由已知可以构造二次函数,利用二次函数性质解决……
C
2
A
B
D
M
x
Q
P
F
E
解:设AM的长为x(m),则BM的长为(2-x)m,以AM和BM为边的两个正方形面积之和为y(m ).
根据题意,
y与x之间的函数表达式为
y=x +(2-x)
=2x -4x+4
=2(x-1) +2
A
B
C
D
M
x
Q
P
F
E
2
∵a=2>0,抛物线开口向上,
∴x=1时,y有最小值,最小是2.
又 ∵自变量x的取值范围为0<x<2,
∴当AM=1m时,截取的板材面积最小,最小面积是2m .
菱形的两条对角线的和为40cm.
(1)如果菱形的面积为s(cm2),一条对角线的长为x(cm2),写出s与x的函数表达式,并指出自变量x的取值范围;
(2)当这两条对角线的长分别为多少时,菱形的面积最大?最大面积是多少?
变式练习
菱形的两条对角线的和为40cm.
(1) 如果菱形的面积为s(cm2),一条对角线的长为x(cm),写出s与x的函数表达式,并指出自变量x的取值范围;
变式练习
菱形的两条对角线的和为40cm.
(2)当这两条对角线的长分别为多少时,菱形的面积最大?最大面积是多少?
变式练习
.
挑战自我
如图,用篱笆围成一个一面靠墙(墙的最大可用长度为10m)、中间隔着一道篱笆的矩形菜园.已知篱笆的长度为24m.设菜园的宽AB为x(m),面积为y(m ).
(1)写出y与x之间的函数表达式及自变量的取值范围;
(2)围成的菜园的最大面积是多少?这时菜园的宽x等于多少?
A
D
B
C
10
分析:设菜园的宽为x (m),
则菜园的长为(24-3x)m,
矩形的面积=长×宽
=(24-3x)x
x
x
x
24-3x
挑战自我
A
D
B
C
10
解:(1)写出y与x之间的函数表达式及自变量的取值范围;
y=x(24-3x)=3x +24x
∴0<24-3x≤10
x<8
∵ BC≤10,∴24-3x≤10,
x
y
o
4
48
8
挑战自我
∴当x= 时,y最大=
y=x(24-3x)
=3x +24x
= -3(x-4)2+48
(2)围成的菜园的最大面积是多少?这时菜园的宽x等于多少?
所以,围成的菜园的最大面积是 m2,这时菜园的宽x等 于 m.
今天你学到了什么?最深的感受是什么?
实际问题
抽象转化
建立函数模型
数学问题
运用
数学知识
问题的解
返回解释
检验
必做题:习题5.7 3题
选做题:习题5.7 7题
当 堂 作 业 题
