青岛版九年级数学下册 5.4 二次函数的图象和性质(第2课时)课件 (共12张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 5.4 二次函数的图象和性质(第2课时)课件 (共12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 690.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 07:29:34 | ||
图片预览



文档简介
(共12张PPT)
5.4 二次函数的图象和性质(2)
你还记得二次函数y=x2的图象是怎样的吗?
开口向上的抛物线,对称轴是y轴,顶点在原点.
y轴左边图象下降, y轴右边图象上升.
那么y=x2+1的图象与y=x2的图象有什么关系?
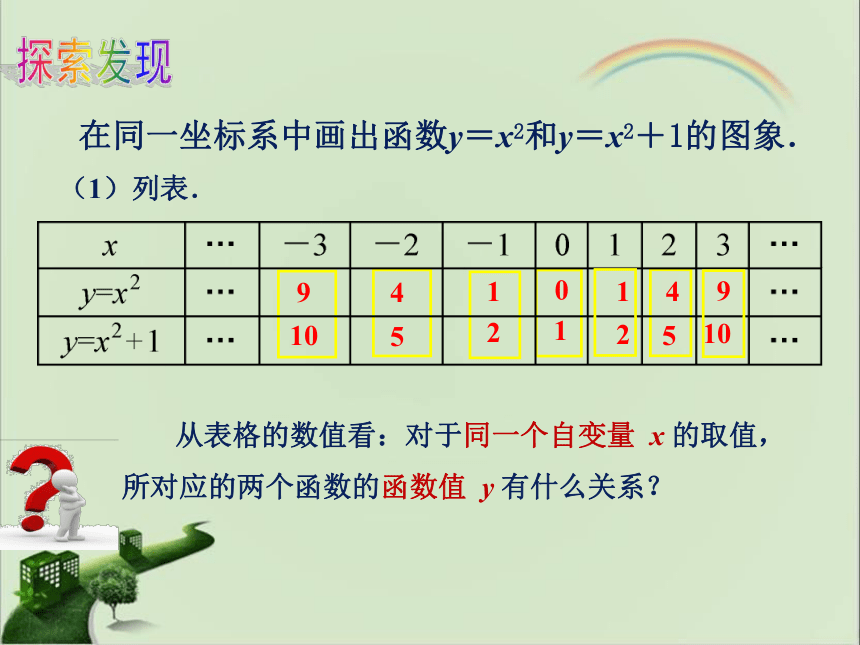
(1)列表.
在同一坐标系中画出函数y=x2和y=x2+1的图象.
从表格的数值看:对于同一个自变量 x 的取值,所对应的两个函数的函数值 y 有什么关系?
4
1
0
1
4
9
9
5
2
1
2
5
10
10
(2)描点、连线.
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
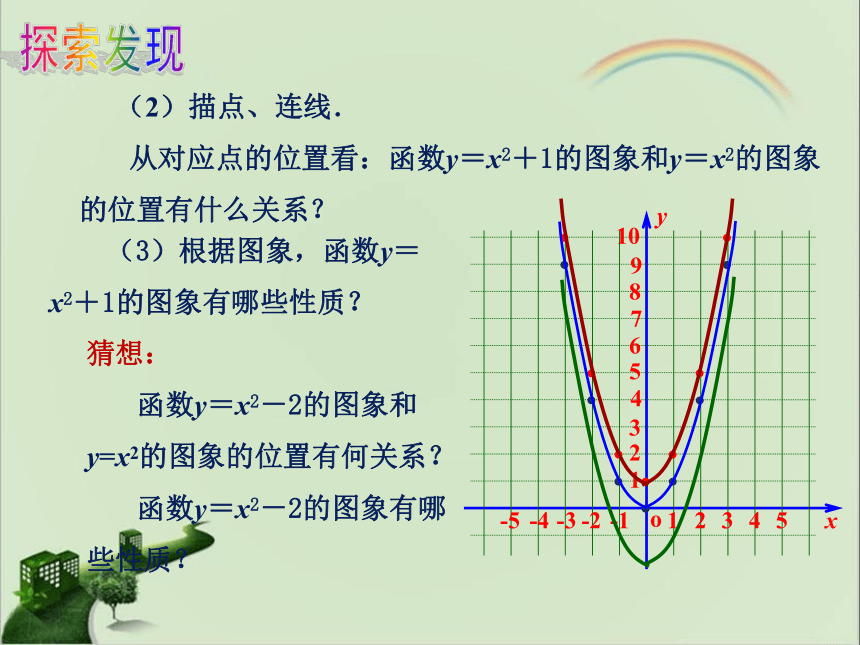
从对应点的位置看:函数y=x2+1的图象和y=x2的图象的位置有什么关系?
(3)根据图象,函数y=x2+1的图象有哪些性质?
猜想:
函数y=x2-2的图象和y=x2的图象的位置有何关系?
函数y=x2-2的图象有哪些性质?
由上面的例子,你发现二次函数y=ax2+k的图象与函数y=ax2的图象有什么关系?
二次函数 y=ax2 + k( k >0)的图象是由二次函数
y=ax2 的图象沿y 轴向__平移__个单位长度得到的一条直线.
二次函数 y=ax2 + k ( k <0)的图象是由二次函数
y=ax2的图象沿 y 轴向__平移 个单位长度得到的一条直线.
上
k
下
|k|
二次函数y=ax2 + k顶点坐标是_ _ ,对称轴是_ _.
(0,k)
y轴
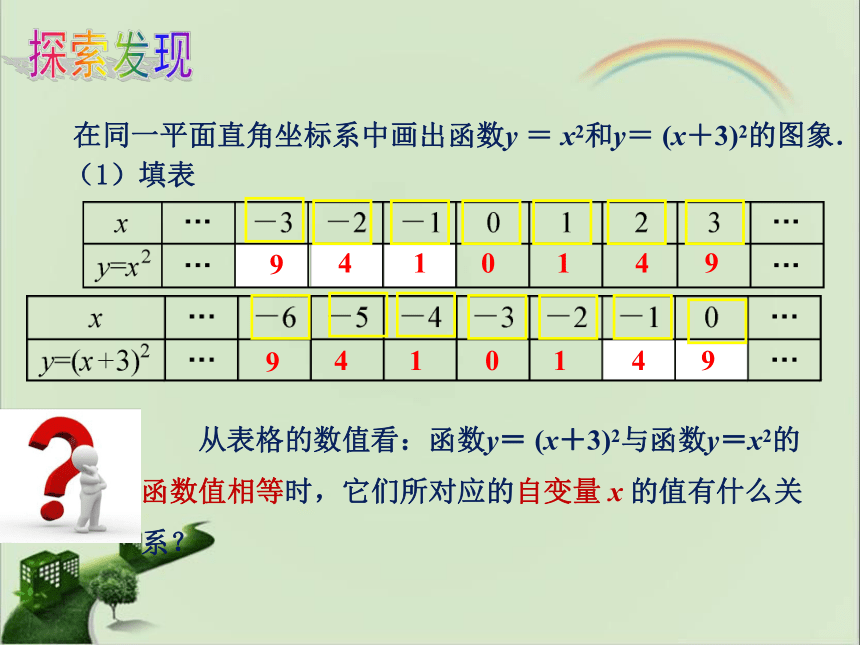
在同一平面直角坐标系中画出函数y = x2和y= (x+3)2的图象.
(1)填表
从表格的数值看:函数y= (x+3)2与函数y=x2的函数值相等时,它们所对应的自变量 x 的值有什么关系?
4
1
0
1
4
9
9
4
1
0
1
4
9
9
(2)描点、连线.
从对应点的位置看:函数y= (x+3)2的图象和y=x2的图象的位置有什么关系?
(3)根据图象,函数y= (x+3)2 的图象有哪些性质?
猜想:
函数y= (x-1)2的图象和y=x2的图象的位置有何关系?
函数y= (x-1)2的图象有哪些性质?
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
-6
从上面的例子,发现二次函数y=a(x+m)2的图象与函数y=ax2的图象有什么关系?
二次函数 y=a(x + m)2( m>0)的图象是由二次函数
y=ax2 的图象沿x轴向__平移__个单位长度得到的一条直线.
二次函数y=a(x + m)2( m<0)的图象是由二次函数
y=ax2的图象沿 x 轴向__平移__个单位长度得到的一条直线.
左
m
右
|m|
二次函数y=ax2 + k顶点坐标是_ _ ,对称轴是_ _ .
(0,k)
y轴
1.将函数y=2x2-2的图象先向 平移 个单位,就得到函数y = 2x2的图象,再向 平移 个单位得到函数y = 2(x-3)2的图象.
2.二次函数y = -3(x+4)2的图象开口 ,由抛物线
y = -3x2向 平移 个单位得到的,当x = 时,
y有最 值,是 .
3.将二次函数y =6x2的图象向右平移1个单位后得到函数 _________的图象,其顶点坐标是 ,当x 时,y随x的增大而增大;当x____时,y随x的增大而减小.
这一节课我们一起学习了哪些知识和方法?
你还有什么疑问吗?
你认为还有继续探索的问题吗?
5.4 二次函数的图象和性质(2)
你还记得二次函数y=x2的图象是怎样的吗?
开口向上的抛物线,对称轴是y轴,顶点在原点.
y轴左边图象下降, y轴右边图象上升.
那么y=x2+1的图象与y=x2的图象有什么关系?
(1)列表.
在同一坐标系中画出函数y=x2和y=x2+1的图象.
从表格的数值看:对于同一个自变量 x 的取值,所对应的两个函数的函数值 y 有什么关系?
4
1
0
1
4
9
9
5
2
1
2
5
10
10
(2)描点、连线.
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
从对应点的位置看:函数y=x2+1的图象和y=x2的图象的位置有什么关系?
(3)根据图象,函数y=x2+1的图象有哪些性质?
猜想:
函数y=x2-2的图象和y=x2的图象的位置有何关系?
函数y=x2-2的图象有哪些性质?
由上面的例子,你发现二次函数y=ax2+k的图象与函数y=ax2的图象有什么关系?
二次函数 y=ax2 + k( k >0)的图象是由二次函数
y=ax2 的图象沿y 轴向__平移__个单位长度得到的一条直线.
二次函数 y=ax2 + k ( k <0)的图象是由二次函数
y=ax2的图象沿 y 轴向__平移 个单位长度得到的一条直线.
上
k
下
|k|
二次函数y=ax2 + k顶点坐标是_ _ ,对称轴是_ _.
(0,k)
y轴
在同一平面直角坐标系中画出函数y = x2和y= (x+3)2的图象.
(1)填表
从表格的数值看:函数y= (x+3)2与函数y=x2的函数值相等时,它们所对应的自变量 x 的值有什么关系?
4
1
0
1
4
9
9
4
1
0
1
4
9
9
(2)描点、连线.
从对应点的位置看:函数y= (x+3)2的图象和y=x2的图象的位置有什么关系?
(3)根据图象,函数y= (x+3)2 的图象有哪些性质?
猜想:
函数y= (x-1)2的图象和y=x2的图象的位置有何关系?
函数y= (x-1)2的图象有哪些性质?
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
-6
从上面的例子,发现二次函数y=a(x+m)2的图象与函数y=ax2的图象有什么关系?
二次函数 y=a(x + m)2( m>0)的图象是由二次函数
y=ax2 的图象沿x轴向__平移__个单位长度得到的一条直线.
二次函数y=a(x + m)2( m<0)的图象是由二次函数
y=ax2的图象沿 x 轴向__平移__个单位长度得到的一条直线.
左
m
右
|m|
二次函数y=ax2 + k顶点坐标是_ _ ,对称轴是_ _ .
(0,k)
y轴
1.将函数y=2x2-2的图象先向 平移 个单位,就得到函数y = 2x2的图象,再向 平移 个单位得到函数y = 2(x-3)2的图象.
2.二次函数y = -3(x+4)2的图象开口 ,由抛物线
y = -3x2向 平移 个单位得到的,当x = 时,
y有最 值,是 .
3.将二次函数y =6x2的图象向右平移1个单位后得到函数 _________的图象,其顶点坐标是 ,当x 时,y随x的增大而增大;当x____时,y随x的增大而减小.
这一节课我们一起学习了哪些知识和方法?
你还有什么疑问吗?
你认为还有继续探索的问题吗?
