青岛版九年级数学下册 5.4 二次函数的图象和性质(3)课件 (共12张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 5.4 二次函数的图象和性质(3)课件 (共12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 850.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 07:27:11 | ||
图片预览





文档简介
(共12张PPT)
二次函数y=a(x-h) +k(a≠0)的图象和性质
5.4 二次函数的图象和性质(3)
如何画二次函数 的图象?
我们来探究二次函数 之间的关系.
二次函数
图象上的点
横坐标
纵坐标
a
a
通过上表说明 之间的关系?
从此表看出:把二次函数 的图象向上平移3个单位,就得到函数 的图象.因此,二次函数 的图象也是抛物线,它的对称轴为直线 x=1 (与抛物线 的对称 轴一样),顶点坐标为(1,3)(它是由抛物线
的顶点(1,0)向上平移3个单位得到),它的开口向上.
函数 的图象是抛物线,它的对称轴是直线 x=h 它的
顶点坐标是 (h,k). 当a >0时,抛物线的开口向上;当a<0时,开口向下.
由于我们已经知道了函数 的图象的性质,因此画 的图象的步骤如下:
第一步:写出对称轴和顶点坐标,并且在平面直角坐标系内画出对称轴,描出顶点;
第三步:利用对称性,画出图象在对称轴左边的部分(这只要先把对称轴左边的对应点描出来,然后用一条光滑曲线顺次连接他们和顶点).
第二步:列表(自变量x从顶点的横坐标开始取值),描点和连线,画出图象在对称轴右边的部分;
解 : 对称轴是直线 x =-1,顶点坐标为(-1,-3)
x -1 0 1 2 3
-3 -2.5 -1 1.5 5
画二次函数 的图象.
列表:自变量x从顶点的横坐标-1开始取值.
2
4
-2
-4
2
4
-2
-4
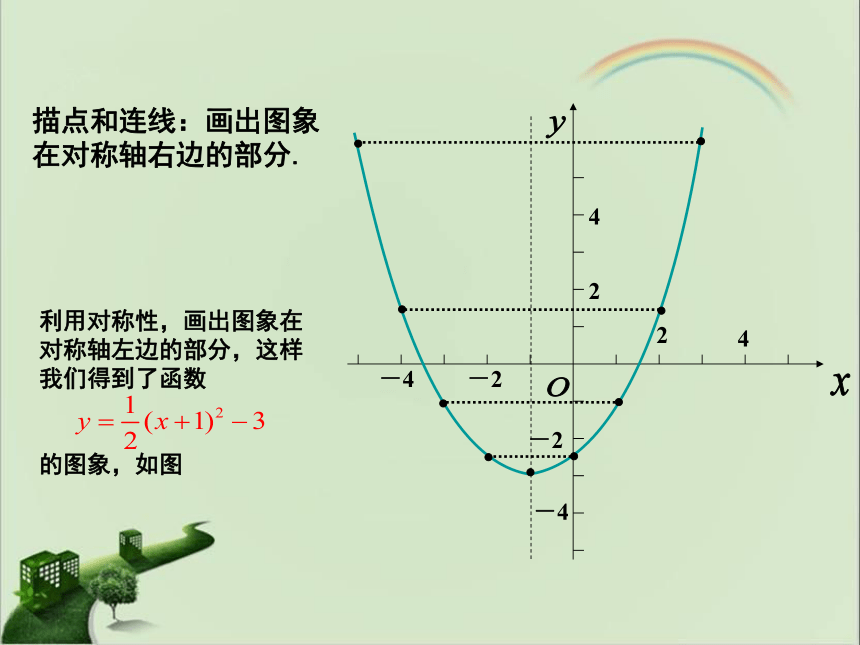
描点和连线:画出图象在对称轴右边的部分.
利用对称性,画出图象在对称轴左边的部分,这样我们得到了函数
的图象,如图
已知某抛物线的顶点坐标为(-2,1),且与y轴相交于点(0,4),求这个抛物线所表示的二次函数的表达式.
解: 由于点(-2,1)是该抛物线的顶点,可设这个抛物线所表示的二次函数的表达式为y=a(x+2) +1.
由函数图象过点(0,4),可得 4=a(0+a) +1,
解得a= .
因此,所求的二次函数表达式为:
1、画二次函数 的图象.
x -2 -1 0 1 2 3 4
2 2.5 3 2.5 2
列 表
描 点
2
4
-2
-4
2
4
-2
-4
2、说出下列二次函数的图象的对称轴、顶点坐标和开口方向:
对称轴为 x = 9
顶点坐标为 (9,7)
∴ 开口方向向上
对称轴为 x = -18
顶点坐标为 (-18,-13)
∴ 开口方向向下
归纳小结
y=a(x-h)2 +k(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
性质
最值
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当xy随着x的增大而减小.
当x>h时,
y随着x的增大而增大.
当xy随着x的增大而增大.
当x>h时,
y随着x的增大而减小.
x=h时,y最小值=k
x=h时,y最大值=k
抛物线y=a(x-h)2+k(a≠0)的图象可由y=a(x-h)2的图象通过上下平移得到.
二次函数y=a(x-h) +k(a≠0)的图象和性质
5.4 二次函数的图象和性质(3)
如何画二次函数 的图象?
我们来探究二次函数 之间的关系.
二次函数
图象上的点
横坐标
纵坐标
a
a
通过上表说明 之间的关系?
从此表看出:把二次函数 的图象向上平移3个单位,就得到函数 的图象.因此,二次函数 的图象也是抛物线,它的对称轴为直线 x=1 (与抛物线 的对称 轴一样),顶点坐标为(1,3)(它是由抛物线
的顶点(1,0)向上平移3个单位得到),它的开口向上.
函数 的图象是抛物线,它的对称轴是直线 x=h 它的
顶点坐标是 (h,k). 当a >0时,抛物线的开口向上;当a<0时,开口向下.
由于我们已经知道了函数 的图象的性质,因此画 的图象的步骤如下:
第一步:写出对称轴和顶点坐标,并且在平面直角坐标系内画出对称轴,描出顶点;
第三步:利用对称性,画出图象在对称轴左边的部分(这只要先把对称轴左边的对应点描出来,然后用一条光滑曲线顺次连接他们和顶点).
第二步:列表(自变量x从顶点的横坐标开始取值),描点和连线,画出图象在对称轴右边的部分;
解 : 对称轴是直线 x =-1,顶点坐标为(-1,-3)
x -1 0 1 2 3
-3 -2.5 -1 1.5 5
画二次函数 的图象.
列表:自变量x从顶点的横坐标-1开始取值.
2
4
-2
-4
2
4
-2
-4
描点和连线:画出图象在对称轴右边的部分.
利用对称性,画出图象在对称轴左边的部分,这样我们得到了函数
的图象,如图
已知某抛物线的顶点坐标为(-2,1),且与y轴相交于点(0,4),求这个抛物线所表示的二次函数的表达式.
解: 由于点(-2,1)是该抛物线的顶点,可设这个抛物线所表示的二次函数的表达式为y=a(x+2) +1.
由函数图象过点(0,4),可得 4=a(0+a) +1,
解得a= .
因此,所求的二次函数表达式为:
1、画二次函数 的图象.
x -2 -1 0 1 2 3 4
2 2.5 3 2.5 2
列 表
描 点
2
4
-2
-4
2
4
-2
-4
2、说出下列二次函数的图象的对称轴、顶点坐标和开口方向:
对称轴为 x = 9
顶点坐标为 (9,7)
∴ 开口方向向上
对称轴为 x = -18
顶点坐标为 (-18,-13)
∴ 开口方向向下
归纳小结
y=a(x-h)2 +k(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
性质
最值
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当x
当x>h时,
y随着x的增大而增大.
当x
当x>h时,
y随着x的增大而减小.
x=h时,y最小值=k
x=h时,y最大值=k
抛物线y=a(x-h)2+k(a≠0)的图象可由y=a(x-h)2的图象通过上下平移得到.
