青岛版九年级数学下册第5章 对函数的再探索 5.5确定二次函数的解析式 课件(共15张PPT)
文档属性
| 名称 | 青岛版九年级数学下册第5章 对函数的再探索 5.5确定二次函数的解析式 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 114.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 20:58:04 | ||
图片预览






文档简介
(共15张PPT)
5.5 确定二次函数的表达式
2.还记得我们是怎样求一次函数和反比例函数的表达式吗?
1.二次函数关系式有哪几种表达方式?
用待定系数法求解.
一般式: y=ax2 + bx+c (a≠0)
顶点式:y = a(x + h)2 + k (a≠0)
知识回顾
交点式:y = a(x-x1)(x-x2) (a≠0)
活动一:图像法判断二次函数解析式
【例1】抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )
随堂练习: 已知二次函数的图象如图所示,则这个二次函数的表达式为( )
A.y=x2﹣2x + 3
B.y=x2﹣2x﹣3
C.y=x2 + 2x﹣3
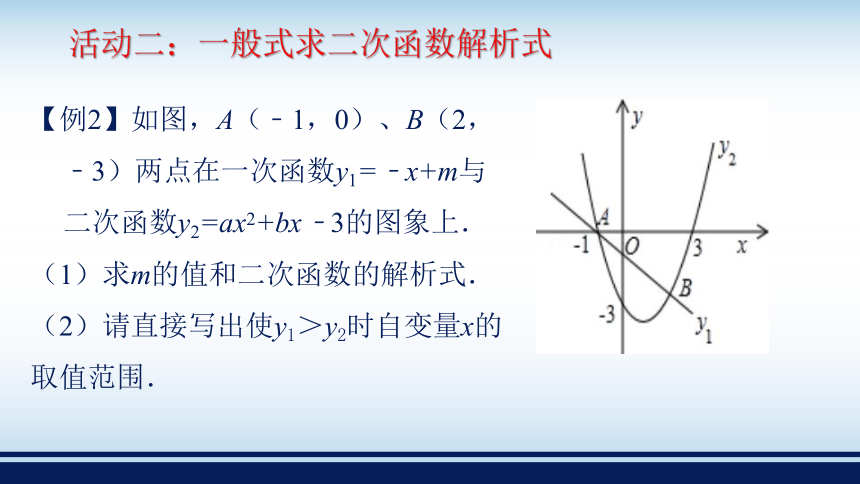
活动二:一般式求二次函数解析式
【例2】如图,A(﹣1,0)、B(2,﹣3)两点在一次函数y1=﹣x+m与二次函数y2=ax2+bx﹣3的图象上.
(1)求m的值和二次函数的解析式.
(2)请直接写出使y1>y2时自变量x的取值范围.
练2. 已知二次函数y=ax2+bx的图象经过点(2,0)、(﹣1,6)
(1)求二次函数的解析式;
(2)不用列表,在下图中画出函数图象,观察图象写出y>0时,x的取值范围.
活动三:待定系数法求二次函数解析式
【例3】(2014 四川达州中学期中)在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
练3. 已知二次函数y=x2+bx+c的图象与y轴交于点A(0,﹣6),与x轴的一个交点坐标是B(﹣2,0).
(1)求二次函数的关系式,并写出顶点坐标;
(2)将二次函数图象沿x轴向左平移2.5个单位长度,求所得图象对应的函数关系式.
【例4】(2014 江西南昌实验中学期末)已知二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),且与x轴交于A、B两点.
(1)试确定此二次函数的解析式;
(2)判断点P(﹣2,3)是否在这个二次函数的图象上?如果在,请求出△PAB的面积;如果不在,试说明理由.
三点式求二次函数解析式
练4. 已知二次函数图象的顶点是(﹣1,2),且过点(0,1.5) .
(1)求二次函数的表达式,并在图中画出它的图象;
(2)求证:对任意实数m,点M(m,-m2)都不在这个二次函数的图象上.
顶点式求二次函数解析式
【例5】(2014 黑龙江双鸭山二中期末)抛物线y=ax2+12x-19顶点横坐标是3,则a= .
练5.已知抛物线y=x2+(m-1)x-0.25的顶点的横坐标是2,则m的值是( )
2.当给出的坐标或点中有顶点,可设顶点式
y = a(x + h)2 + k,将h、k换为顶点坐标,再将另一点的坐标代入即可求出a的值.
方法总结
1.求二次函数y=ax2 + bx+c的表达式,关键是求出待定系数a,b,c的值,由已知条件列出关于a,b,c的方程或方程组,求出a,b,c,就可以写出二次函数的表达式.
课堂练习
根据下列已知条件,选择合适的方法求二次函数的表达式:
1.已知二次函数y=ax2 + bx的图像经过点(-2,8)
和(-1,5),求这个二次函数的表达式.
2.已知二次函数的图象经过原点,且当x=1时,y有最小值-1, 求这个二次函数的表达式.
拓展延伸
如图所示,已知抛物线的对称轴是过(3,0)的直线,它与x轴交于A、B两点,与y轴交于C点,点A 、C的坐标分别是(8,0) 、(0,4),求这个抛物线的表达式.
分享收获
课堂小结,感悟收获
你学到哪些二次函数表达式的求法?
5.5 确定二次函数的表达式
2.还记得我们是怎样求一次函数和反比例函数的表达式吗?
1.二次函数关系式有哪几种表达方式?
用待定系数法求解.
一般式: y=ax2 + bx+c (a≠0)
顶点式:y = a(x + h)2 + k (a≠0)
知识回顾
交点式:y = a(x-x1)(x-x2) (a≠0)
活动一:图像法判断二次函数解析式
【例1】抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )
随堂练习: 已知二次函数的图象如图所示,则这个二次函数的表达式为( )
A.y=x2﹣2x + 3
B.y=x2﹣2x﹣3
C.y=x2 + 2x﹣3
活动二:一般式求二次函数解析式
【例2】如图,A(﹣1,0)、B(2,﹣3)两点在一次函数y1=﹣x+m与二次函数y2=ax2+bx﹣3的图象上.
(1)求m的值和二次函数的解析式.
(2)请直接写出使y1>y2时自变量x的取值范围.
练2. 已知二次函数y=ax2+bx的图象经过点(2,0)、(﹣1,6)
(1)求二次函数的解析式;
(2)不用列表,在下图中画出函数图象,观察图象写出y>0时,x的取值范围.
活动三:待定系数法求二次函数解析式
【例3】(2014 四川达州中学期中)在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
练3. 已知二次函数y=x2+bx+c的图象与y轴交于点A(0,﹣6),与x轴的一个交点坐标是B(﹣2,0).
(1)求二次函数的关系式,并写出顶点坐标;
(2)将二次函数图象沿x轴向左平移2.5个单位长度,求所得图象对应的函数关系式.
【例4】(2014 江西南昌实验中学期末)已知二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),且与x轴交于A、B两点.
(1)试确定此二次函数的解析式;
(2)判断点P(﹣2,3)是否在这个二次函数的图象上?如果在,请求出△PAB的面积;如果不在,试说明理由.
三点式求二次函数解析式
练4. 已知二次函数图象的顶点是(﹣1,2),且过点(0,1.5) .
(1)求二次函数的表达式,并在图中画出它的图象;
(2)求证:对任意实数m,点M(m,-m2)都不在这个二次函数的图象上.
顶点式求二次函数解析式
【例5】(2014 黑龙江双鸭山二中期末)抛物线y=ax2+12x-19顶点横坐标是3,则a= .
练5.已知抛物线y=x2+(m-1)x-0.25的顶点的横坐标是2,则m的值是( )
2.当给出的坐标或点中有顶点,可设顶点式
y = a(x + h)2 + k,将h、k换为顶点坐标,再将另一点的坐标代入即可求出a的值.
方法总结
1.求二次函数y=ax2 + bx+c的表达式,关键是求出待定系数a,b,c的值,由已知条件列出关于a,b,c的方程或方程组,求出a,b,c,就可以写出二次函数的表达式.
课堂练习
根据下列已知条件,选择合适的方法求二次函数的表达式:
1.已知二次函数y=ax2 + bx的图像经过点(-2,8)
和(-1,5),求这个二次函数的表达式.
2.已知二次函数的图象经过原点,且当x=1时,y有最小值-1, 求这个二次函数的表达式.
拓展延伸
如图所示,已知抛物线的对称轴是过(3,0)的直线,它与x轴交于A、B两点,与y轴交于C点,点A 、C的坐标分别是(8,0) 、(0,4),求这个抛物线的表达式.
分享收获
课堂小结,感悟收获
你学到哪些二次函数表达式的求法?
