青岛版九年级数学下册5.6 二次函数的图象与一元二次方程 课件(共27张PPT)
文档属性
| 名称 | 青岛版九年级数学下册5.6 二次函数的图象与一元二次方程 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 08:51:34 | ||
图片预览







文档简介
(共27张PPT)
ax2+bx+c=0
y=ax2+bx+c
5.6二次函数的图象与一元二次方程
思考回顾
1、若关于x的一元二次方程(a﹣1)x2﹣x+1=0有实数根,则a的取值范围为 .
一元二次方程ax +bx+c=0(a≠0)根的判别式
(1)Δ>0 方程有两个不相等的实数根;(2)Δ=0 方程有两个相等的实数根;(3)Δ<0 方程没有实数根.
思考回顾
2.已知关于x的方程mx2﹣(m+2)x+2=0(m≠0).(1)求证:方程总有两个实数根;(2)若方程的两个实数根都是整数,求正整数m的值.
思考回顾
二次函数y=(a≠0) 的图象和性质:
1、对称轴是 _________ ,顶点坐标是________ 。
2、当对称轴在y轴左侧时,
3、当对称轴在y轴右侧时,
4、它与y轴交点坐标为
5、求它与x轴的交点坐标
令y=0,即0=ax +bx+c
一元二次方程
(0,c)
a,b同号.(左同)
a,b异号.(右异)
-
2a
b
—
x=
-
2a
b
—
4ac-b
4a
,
( )
学习目标
1.探索抛物线与x轴的交点横坐标和一元二次方程的根的关系,体会方程与函数的密切关系;
2.学会用图像法求一元二次方程近似根;
(1)比较二次函数的表达式与一元二次方程=0,你能说出二者之间有什么联系吗?
观察与思考 一
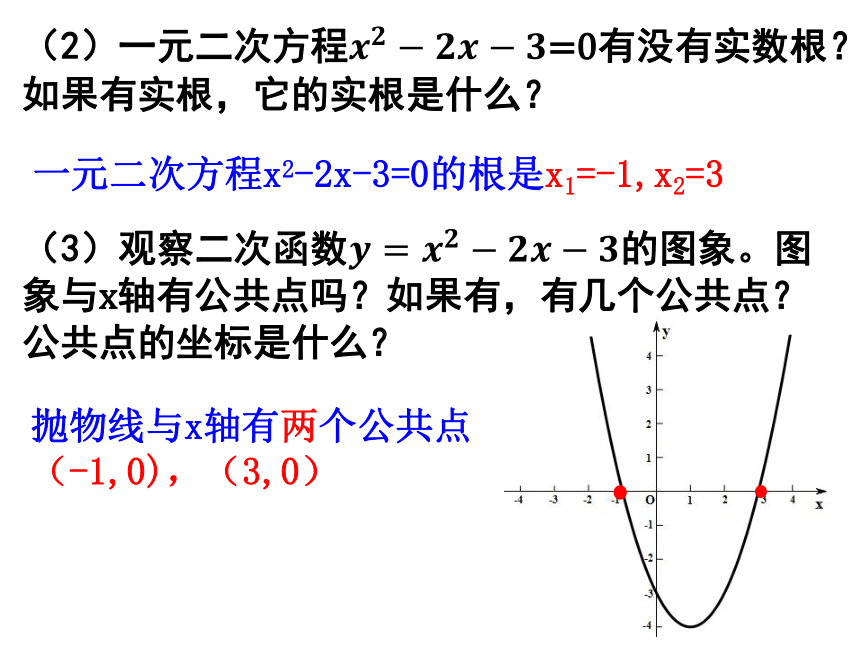
(2)一元二次方程=0有没有实数根?如果有实根,它的实根是什么?
(3)观察二次函数的图象。图象与x轴有公共点吗?如果有,有几个公共点?公共点的坐标是什么?
一元二次方程x2-2x-3=0的根是x1=-1,x2=3
抛物线与x轴有两个公共点
(-1,0),(3,0)
(4)x为何值时,函数的值是0?
(5)一元二次方程=0的实根和二次函数的图象与x轴的交点的横坐标有什么关系
一元二次方程x2-2x-3=0的根是x1=-1,x2=3
抛物线与x轴有两个公共点
(-1,0),(3,0)
当x=-1,x=3时,函数y的值是0.即x2-2x-3=0。
相等
观察与思考 二
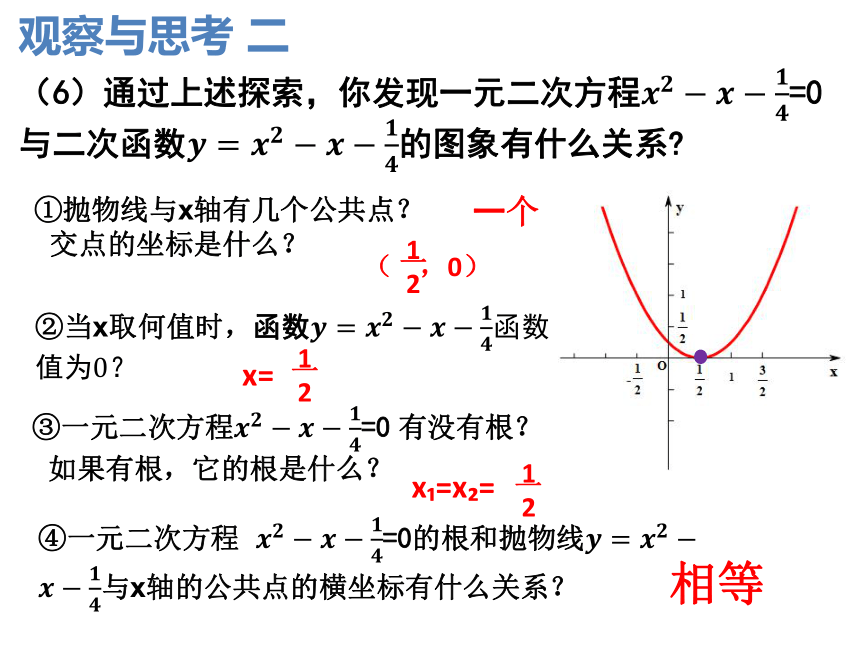
(6)通过上述探索,你发现一元二次方程=0与二次函数的图象有什么关系
①抛物线与x轴有几个公共点?
交点的坐标是什么?
③一元二次方程=0 有没有根?
如果有根,它的根是什么?
④一元二次方程 =0的根和抛物线与x轴的公共点的横坐标有什么关系?
②当x取何值时,函数函数值为0?
一个
1
2
一
( ,0)
1
2
一
x=
1
2
一
x =x =
相等
1、抛物线y=ax +bx+c与x轴公共点的横坐标,
恰为一元二次方程ax +bx+c=0的实根。
2、若一元二次方程ax +bx+c=0有实根,则
抛物线y=ax +bx+c与x轴有公共点,且
公共点的横坐标是这个一元二次方程的实根。
(7)一般地,一元二次方程=0有实根,那么该方程的根和二次函数的图象与x轴的交点的横坐标有什么关系
y=x -2x-3
抛物线y=ax2+bx+c
与x轴有公共点
二次方程ax2+bx+c=0
有实根
转化为
转化为
二次函数的图象与一元二次方程
1.在平面直角坐标系xOy中,二次函数y=ax2+bx+1的图象如图所示,则方程ax2+bx+1=0的根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根C.没有实数根
D.无法判断
B
小试牛刀
2、已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+=0的根的情况是( )
A.无实数根 B.有两个相等实数根C.有两个异号实数根 D.有两个同号不等实数根
D
3.二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx=﹣m有实数根,则m最大值为( )
A.3 B.﹣3
C.﹣6 D.9
A
解:由图象可得,二次函数y=ax2+bx的最小值是y=﹣3,∵一元二次方程ax2+bx=﹣m有实数根,∴﹣m≥﹣3,解得,m≤3,∴m的最大值是3,
例1
用图象法讨论一元二次方程x -3x-2=0的根
解:
(1)画抛物线y=x -3x-2.
(2)由图象可知,在-1与0 之间以及 3与4之间各有一个根.
分别计算x=0,x=-1,x=-0.5的函数值,列表如下:
x
y
-1
-0.5
0
2
-0.25
-2
由于当x=-1时,y>0,当x=-0.5时,y<0,所以方程的根在-1和-0.5之间。
由于在画图和观察过程中
存在误差,所以得到的往往
是二次方程根的近似值
(精确到0.1)
可再将-1和-0.5之间分为5等份,每个分点作为x值,利用计算器求出所对应的函数值,列表:
x
y
-1.0
-0.7
-0.9
-0.8
2
-0.5
-0.6
1.04
1.51
0.16
0.59
-0.25
可以看出,这个根在-0.6和-0.5之间,由于本题要求精确到0.1,所以可以将-0.6或-0.5看作二次方程
x2-3x-2=0较小根的近似值,即二次方程x2-3x-2=0的较小根为x≈-0.6或x≈-0.5
你能求出二次方程
x2-3x-2=0较大根
的近似值吗?试试看!
同样的,可以求出一元二次方程x2-3x-2=0的较大根的近似值,列表如下:
由上表可见,方程的较大根在3.5和3.6之间,所以可以将3.5或3.6看作二次方程x2-3x-2=0较大根的近似值,即二次方程x2-3x-2=0的较大根为x≈3.5或x≈3.6
3.0
-0.25
-2
0.16
3.7
3.6
3.5
1.04
0.59
3.9
3.8
2
1.51
4.0
x
y
1.下表是满足二次函数y=ax2+bx+c的五组数据,x1是方程ax2+bx+c=0的一个解,则下列选项中正确的是( )
x 1.6 1.8 2.0 2.2 2.4
y ﹣0.80 ﹣0.54 ﹣0.20 0.22 0.72
A.1.6<x1<1.8
B.1.8<x1<2.0
C.2.0<x1<2.2
D.2.2<x1<2.4
C
例2
用图象法讨论一元二次方程x -2x+3=0的根。
x
y
解:
(1)画出抛物线y=x -2x+3
(2)由于图象与x轴没有公共点,所以一元二次方程x -2x+3=0没有实数根
抛物线y=ax2+bx+c
与x轴无公共点
二次方程ax2+bx+c=0
无实根
转化为
转化为
x
y
挑战自我
已知抛物线,当a,b,c满足什么条件时,
(1)抛物线与x轴有两个公共点?
(2)抛物线与x轴有一个公共点?
(3)抛物线与x轴没有公共点?
一元二次方程根的判别式
b -4ac>0
b -4ac=0
b -4ac<0
1、若方程ax2﹣2ax+c=0(a≠0)有一个根为x=﹣1,那么抛物线y=ax2﹣2ax+c与x轴两交点间的距离为 .
跟踪练习
4
解:抛物线的对称轴是直线x=﹣ =1.
∴方程ax2﹣2ax+c=0(a≠0)的另一根为x=3.则两交点间的距离为4.
2、抛物线y=ax2+bx+c经过点A(﹣2,0)、B(1,0)两点,则关于x的一元二次方程a(x﹣3)2+c=3b﹣bx的解是 .
x =1,x =4
解:∵a(x﹣3)2+c=3b﹣bx,∴a(x﹣3)2+b(x﹣3)+c=0,∵抛物线y=ax2+bx+c经过点A(﹣2,0)、B(1,0),∴x﹣3=﹣2或1,∴a(x﹣3)2+c=3b﹣bx的解是1或4
3、抛物线与x轴的交点情况是( )
A.有两个交点 B.只有一个交点 C.没有交点 D.无法判断
4、已知二次函数y=(k﹣2)2x2+(2k+1)x+1与x轴有交点,则k的取值范围是( )
A且 B.且
C. D.
D
A
二次函数y=ax2+bx+c的图象
二次方程ax2+bx+c=0的根
二次函数y=ax2+bx+c的图象与x轴的公共点的个数
二次方程ax2+bx+c=0的根的判别式
两个公共点
一个公共点
没有公共点
有两个不等实根
有两个相等实根
没有实根
=0
>0
<0
课堂小结:
1、二次函数y=ax2+bx+c的图象与一元二次方程 ax2+bx+c=0的关系。
2、根据二次函数的系数,判断它的图象与x轴的位置关系。
1.已知函数y=x2+(m+3)x+2m+2(1)判断该函数的图象与x轴的交点个数.(2)若m=﹣5,求出函数值y在0<x<5时的取值范围.(3)若方程x2﹣2x﹣8=k在0<x<5内有且只有一个解,直接写出k的范围.
拓展与延伸
解:(1)∵△=(m+3)2﹣4(2m+2)=m2﹣2m+1=(m﹣1)2,∴当m=1时,图象与x轴只有一个交点,当m≠1时,图象与x轴有两个交点; (2)m=﹣5时,y=x2﹣2x﹣8=(x﹣1)2﹣9,当x=1时,函数有最小值﹣9,当x=5时,y=7,
(3)若方程x2﹣2x﹣8=k在0<x<5内有且只有一个解,即为y=x2﹣2x﹣8和函数y=k只有一个交点,函数y=x2﹣2x﹣8,与y轴的交点为:(0,﹣8),函数的顶点坐标为:(1,﹣9),故在0<x<5时,y=x2﹣2x﹣8和函数y=k只有一个交点时,k=﹣9或﹣8≤k<7.
2.如图是抛物线y=ax2+bx+c(a≠0),其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,下列结论:①b>0;②2a+b=0;③4a﹣2b+c<0;④a+b+c>0;⑤关于x的方程0=ax2+bx+c的另一个解在﹣2和﹣3之间,其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
D
ax2+bx+c=0
y=ax2+bx+c
5.6二次函数的图象与一元二次方程
思考回顾
1、若关于x的一元二次方程(a﹣1)x2﹣x+1=0有实数根,则a的取值范围为 .
一元二次方程ax +bx+c=0(a≠0)根的判别式
(1)Δ>0 方程有两个不相等的实数根;(2)Δ=0 方程有两个相等的实数根;(3)Δ<0 方程没有实数根.
思考回顾
2.已知关于x的方程mx2﹣(m+2)x+2=0(m≠0).(1)求证:方程总有两个实数根;(2)若方程的两个实数根都是整数,求正整数m的值.
思考回顾
二次函数y=(a≠0) 的图象和性质:
1、对称轴是 _________ ,顶点坐标是________ 。
2、当对称轴在y轴左侧时,
3、当对称轴在y轴右侧时,
4、它与y轴交点坐标为
5、求它与x轴的交点坐标
令y=0,即0=ax +bx+c
一元二次方程
(0,c)
a,b同号.(左同)
a,b异号.(右异)
-
2a
b
—
x=
-
2a
b
—
4ac-b
4a
,
( )
学习目标
1.探索抛物线与x轴的交点横坐标和一元二次方程的根的关系,体会方程与函数的密切关系;
2.学会用图像法求一元二次方程近似根;
(1)比较二次函数的表达式与一元二次方程=0,你能说出二者之间有什么联系吗?
观察与思考 一
(2)一元二次方程=0有没有实数根?如果有实根,它的实根是什么?
(3)观察二次函数的图象。图象与x轴有公共点吗?如果有,有几个公共点?公共点的坐标是什么?
一元二次方程x2-2x-3=0的根是x1=-1,x2=3
抛物线与x轴有两个公共点
(-1,0),(3,0)
(4)x为何值时,函数的值是0?
(5)一元二次方程=0的实根和二次函数的图象与x轴的交点的横坐标有什么关系
一元二次方程x2-2x-3=0的根是x1=-1,x2=3
抛物线与x轴有两个公共点
(-1,0),(3,0)
当x=-1,x=3时,函数y的值是0.即x2-2x-3=0。
相等
观察与思考 二
(6)通过上述探索,你发现一元二次方程=0与二次函数的图象有什么关系
①抛物线与x轴有几个公共点?
交点的坐标是什么?
③一元二次方程=0 有没有根?
如果有根,它的根是什么?
④一元二次方程 =0的根和抛物线与x轴的公共点的横坐标有什么关系?
②当x取何值时,函数函数值为0?
一个
1
2
一
( ,0)
1
2
一
x=
1
2
一
x =x =
相等
1、抛物线y=ax +bx+c与x轴公共点的横坐标,
恰为一元二次方程ax +bx+c=0的实根。
2、若一元二次方程ax +bx+c=0有实根,则
抛物线y=ax +bx+c与x轴有公共点,且
公共点的横坐标是这个一元二次方程的实根。
(7)一般地,一元二次方程=0有实根,那么该方程的根和二次函数的图象与x轴的交点的横坐标有什么关系
y=x -2x-3
抛物线y=ax2+bx+c
与x轴有公共点
二次方程ax2+bx+c=0
有实根
转化为
转化为
二次函数的图象与一元二次方程
1.在平面直角坐标系xOy中,二次函数y=ax2+bx+1的图象如图所示,则方程ax2+bx+1=0的根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根C.没有实数根
D.无法判断
B
小试牛刀
2、已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+=0的根的情况是( )
A.无实数根 B.有两个相等实数根C.有两个异号实数根 D.有两个同号不等实数根
D
3.二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx=﹣m有实数根,则m最大值为( )
A.3 B.﹣3
C.﹣6 D.9
A
解:由图象可得,二次函数y=ax2+bx的最小值是y=﹣3,∵一元二次方程ax2+bx=﹣m有实数根,∴﹣m≥﹣3,解得,m≤3,∴m的最大值是3,
例1
用图象法讨论一元二次方程x -3x-2=0的根
解:
(1)画抛物线y=x -3x-2.
(2)由图象可知,在-1与0 之间以及 3与4之间各有一个根.
分别计算x=0,x=-1,x=-0.5的函数值,列表如下:
x
y
-1
-0.5
0
2
-0.25
-2
由于当x=-1时,y>0,当x=-0.5时,y<0,所以方程的根在-1和-0.5之间。
由于在画图和观察过程中
存在误差,所以得到的往往
是二次方程根的近似值
(精确到0.1)
可再将-1和-0.5之间分为5等份,每个分点作为x值,利用计算器求出所对应的函数值,列表:
x
y
-1.0
-0.7
-0.9
-0.8
2
-0.5
-0.6
1.04
1.51
0.16
0.59
-0.25
可以看出,这个根在-0.6和-0.5之间,由于本题要求精确到0.1,所以可以将-0.6或-0.5看作二次方程
x2-3x-2=0较小根的近似值,即二次方程x2-3x-2=0的较小根为x≈-0.6或x≈-0.5
你能求出二次方程
x2-3x-2=0较大根
的近似值吗?试试看!
同样的,可以求出一元二次方程x2-3x-2=0的较大根的近似值,列表如下:
由上表可见,方程的较大根在3.5和3.6之间,所以可以将3.5或3.6看作二次方程x2-3x-2=0较大根的近似值,即二次方程x2-3x-2=0的较大根为x≈3.5或x≈3.6
3.0
-0.25
-2
0.16
3.7
3.6
3.5
1.04
0.59
3.9
3.8
2
1.51
4.0
x
y
1.下表是满足二次函数y=ax2+bx+c的五组数据,x1是方程ax2+bx+c=0的一个解,则下列选项中正确的是( )
x 1.6 1.8 2.0 2.2 2.4
y ﹣0.80 ﹣0.54 ﹣0.20 0.22 0.72
A.1.6<x1<1.8
B.1.8<x1<2.0
C.2.0<x1<2.2
D.2.2<x1<2.4
C
例2
用图象法讨论一元二次方程x -2x+3=0的根。
x
y
解:
(1)画出抛物线y=x -2x+3
(2)由于图象与x轴没有公共点,所以一元二次方程x -2x+3=0没有实数根
抛物线y=ax2+bx+c
与x轴无公共点
二次方程ax2+bx+c=0
无实根
转化为
转化为
x
y
挑战自我
已知抛物线,当a,b,c满足什么条件时,
(1)抛物线与x轴有两个公共点?
(2)抛物线与x轴有一个公共点?
(3)抛物线与x轴没有公共点?
一元二次方程根的判别式
b -4ac>0
b -4ac=0
b -4ac<0
1、若方程ax2﹣2ax+c=0(a≠0)有一个根为x=﹣1,那么抛物线y=ax2﹣2ax+c与x轴两交点间的距离为 .
跟踪练习
4
解:抛物线的对称轴是直线x=﹣ =1.
∴方程ax2﹣2ax+c=0(a≠0)的另一根为x=3.则两交点间的距离为4.
2、抛物线y=ax2+bx+c经过点A(﹣2,0)、B(1,0)两点,则关于x的一元二次方程a(x﹣3)2+c=3b﹣bx的解是 .
x =1,x =4
解:∵a(x﹣3)2+c=3b﹣bx,∴a(x﹣3)2+b(x﹣3)+c=0,∵抛物线y=ax2+bx+c经过点A(﹣2,0)、B(1,0),∴x﹣3=﹣2或1,∴a(x﹣3)2+c=3b﹣bx的解是1或4
3、抛物线与x轴的交点情况是( )
A.有两个交点 B.只有一个交点 C.没有交点 D.无法判断
4、已知二次函数y=(k﹣2)2x2+(2k+1)x+1与x轴有交点,则k的取值范围是( )
A且 B.且
C. D.
D
A
二次函数y=ax2+bx+c的图象
二次方程ax2+bx+c=0的根
二次函数y=ax2+bx+c的图象与x轴的公共点的个数
二次方程ax2+bx+c=0的根的判别式
两个公共点
一个公共点
没有公共点
有两个不等实根
有两个相等实根
没有实根
=0
>0
<0
课堂小结:
1、二次函数y=ax2+bx+c的图象与一元二次方程 ax2+bx+c=0的关系。
2、根据二次函数的系数,判断它的图象与x轴的位置关系。
1.已知函数y=x2+(m+3)x+2m+2(1)判断该函数的图象与x轴的交点个数.(2)若m=﹣5,求出函数值y在0<x<5时的取值范围.(3)若方程x2﹣2x﹣8=k在0<x<5内有且只有一个解,直接写出k的范围.
拓展与延伸
解:(1)∵△=(m+3)2﹣4(2m+2)=m2﹣2m+1=(m﹣1)2,∴当m=1时,图象与x轴只有一个交点,当m≠1时,图象与x轴有两个交点; (2)m=﹣5时,y=x2﹣2x﹣8=(x﹣1)2﹣9,当x=1时,函数有最小值﹣9,当x=5时,y=7,
(3)若方程x2﹣2x﹣8=k在0<x<5内有且只有一个解,即为y=x2﹣2x﹣8和函数y=k只有一个交点,函数y=x2﹣2x﹣8,与y轴的交点为:(0,﹣8),函数的顶点坐标为:(1,﹣9),故在0<x<5时,y=x2﹣2x﹣8和函数y=k只有一个交点时,k=﹣9或﹣8≤k<7.
2.如图是抛物线y=ax2+bx+c(a≠0),其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,下列结论:①b>0;②2a+b=0;③4a﹣2b+c<0;④a+b+c>0;⑤关于x的方程0=ax2+bx+c的另一个解在﹣2和﹣3之间,其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
D
