青岛版九年级数学下册5.7 二次函数的应用课件(共23张PPT)
文档属性
| 名称 | 青岛版九年级数学下册5.7 二次函数的应用课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 09:02:14 | ||
图片预览






文档简介
(共23张PPT)
5.7二次函数的应用(1)
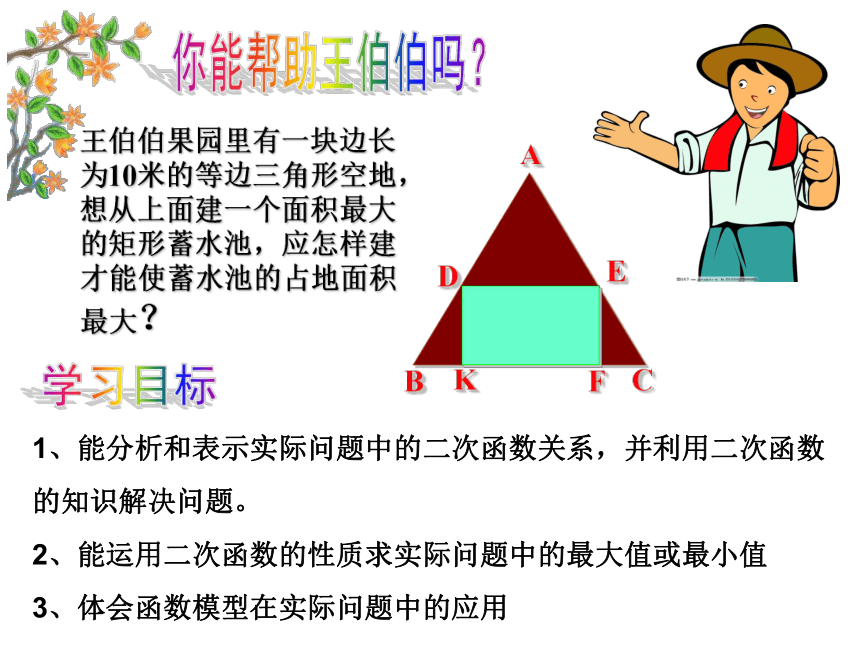
1、能分析和表示实际问题中的二次函数关系,并利用二次函数的知识解决问题。
2、能运用二次函数的性质求实际问题中的最大值或最小值
3、体会函数模型在实际问题中的应用
A
B
C
D
E
F
K
王伯伯果园里有一块边长为10米的等边三角形空地,想从上面建一个面积最大的矩形蓄水池,应怎样建才能使蓄水池的占地面积最大?
1、二次函数y=ax2+bx+c(a≠0)何时有最大值或最小值?
2、如何求二次函数的最值?
配方法
公式法
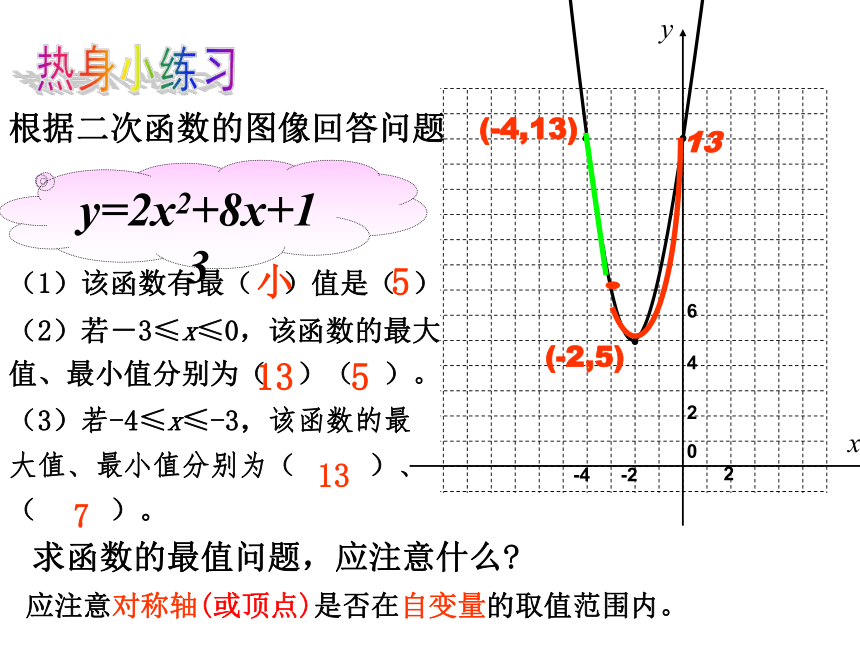
根据二次函数的图像回答问题
y=2x2+8x+13
-2
0
2
4
6
2
-4
x
y
(2)若-3≤x≤0,该函数的最大值、最小值分别为( )( )。
(3)若-4≤x≤-3,该函数的最大值、最小值分别为( )、( )。
应注意对称轴(或顶点)是否在自变量的取值范围内。
13
13
13
(-4,13)
(-2,5)
5
7
求函数的最值问题,应注意什么
(1)该函数有最( )值是( )
小
5
例1.修建有一条边靠墙的矩形菜园,不靠墙的的三边的长度之
和为60m.应怎样设计才使菜园面积最大?最大面积是多少?
解:如图设菜园的宽为x(m),面积为y(m2),则菜园的长为 (60-2 x )(m)
依题意y与x之间的函数解析式为
60-2x
y
所以,当菜园的宽为15 m时菜园面积最大。最大面积是450m2
x
x
y=x(60-2x)
=- 2x2+60x
=-2(x-15) 2 +450
∴当x=15时,y有最大值,最大值是450
例1.修建有一条边靠墙的矩形菜园,不靠墙的的三边的长度之
和为60m.应怎样设计才使菜园面积最大?最大面积是多少?
解:如图,设菜园的长为x(m),面积为y(m2),则菜园的宽为
(m)
依题意y与x之间的函数解析式为
y
所以,当菜园的长为30 m时菜园面积最大。最大面积是450m2
x
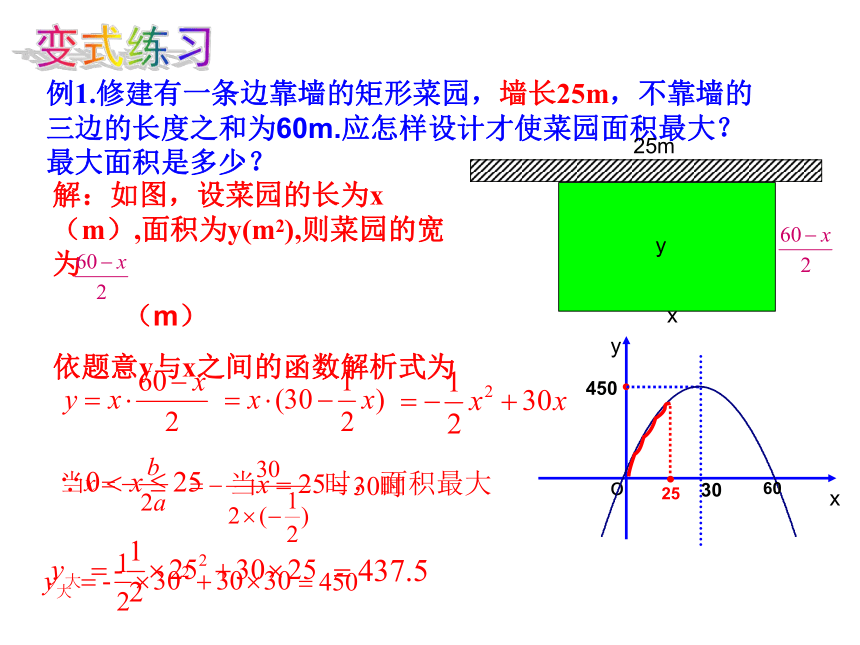
例1.修建有一条边靠墙的矩形菜园,墙长25m,不靠墙的
三边的长度之和为60m.应怎样设计才使菜园面积最大?
最大面积是多少?
解:如图,设菜园的长为x(m),面积为y(m2),则菜园的宽为
(m)
依题意y与x之间的函数解析式为
y
x
25m
x
y
o
30
450
60
25
我们是如何运用二次函数求实际问题中的最大值或最小值
首先应当求出函数解析式和自变量的取值范围,
然后通过配方变形,或利用公式求它的最大值或最小值。
注意:由此求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内 。
例2:如图,ABCD是一块边长为2 m的正方形铁板,在边AB上选取一点M,分别以AM和MB为边截取两块相邻的正方形板料。当AM的长为何值时,截取的板料面积最小?
D
2m
X
A
B
C
M
解:设AM的长为x(m),则BM的长为(2-x)m,以AM和MB为边的两块正方形面积之和为y.依题意得y与x之间的函数解析式为
所以,当AM的长为1m时,截取的板料面积最小,最小面积为2m2.
2-x
y=x2+(2-x)2
=2x2-4x+4
(2017泰安中考第20题)如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19cm2 B.16cm2
C.15cm2 D.12cm2
C
(2016年绍兴中考)用长为8米的铝合金制成如图窗框,问窗框的宽和高各多少米时,窗户的透光面积最大?最大面积是多少?
解:设矩形窗框的宽为x米, 面积为y,由题意得,
今天你学到了什么?最深的感受是什么?
实际问题
抽象转化
建立函数模型
数学问题
运用
数学知识
问题的解
返回解释
检验
王伯伯果园里有一块边长为10米的等边三角形空地,想从上面建一个面积最大的矩形蓄水池,应怎样建?才能使蓄水池的占地面积最大?
A
B
C
D
E
F
K
已知直角三角形的两直角边的和为2。求斜边长可能达到的最小值,以及当斜边长达到最小值时两条直角边的长分别为多少?
A
B
C
2 如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,点P从点A开始沿AB边向点B以2厘米/秒的速度移动,点Q从点B开始沿BC边向点C以1厘米/秒的速度移动,如果P,Q分别
从A,B同时出发,几秒后
ΔPBQ的面积最大?
最大面积是多少?
A
B
C
P
Q
解:根据题意,设经过x秒后ΔPBQ的面积y最大,则:
AP=2x cm PB=(8-2x ) cm
QB=x cm
则 y=1/2 x(8-2x)
=-x2 +4x
=-(x2 -4x +4 -4)
= -(x - 2)2 + 4
所以,当P、Q同时运动2秒后ΔPBQ的面积y最大
最大面积是 4 cm2
(0A
B
C
P
Q
问题5:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
A
B
C
D
解:
(1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
(2)当x= 时,S最大值= =36(平方米)
∴ S=x(24-4x)
=-4x2+24 x (0∴ 0<24-4x ≤8 4≤x<6
∴当x=4m时,S最大值=32 平方米
2、用长为8米的铝合金制成如图窗框,一边靠2m的墙问窗框的宽和高各为多少米时,窗户的透光面积最大?最大面积是多少?
解:设窗框的一边长为x米,
x
又令该窗框的透光面积为y米,那么:
y= x
即:y=-0.5x2+4x
则另一边的长为 米,
小试牛刀
x
y
o
4
48
8
挑战自我
如图,用篱笆围成一个一面靠墙(墙的最大可用长度为10m)、中间隔着一道篱笆的矩形菜园.已知篱笆的长度为24m.设菜园的宽AB为x(m),面积为y(m ).
(1)写出y与x之间的函数表达式及自变量的取值范围;
(2)围成的菜园的最大面积是多少?这时菜园的宽x等于多少?
A
D
B
C
10
y= -3x +24x
当x=4时,y大=48
当x= 时,y大=
x
y
o
12
48
24
挑战自我
如图,用篱笆围成一个一面靠墙(墙的最大可用长度为10m)、中间隔着一道篱笆的矩形菜园.已知篱笆的长度为24m.设菜园的宽AB为x(m),面积为y(m ).
(1)写出y与x之间的函数表达式及自变量的取值范围;
(2)围成的菜园的最大面积是多少?这时菜园的宽x等于多少?
A
D
B
C
10
x
y
10
当x=10 时,y大=
小结:应用二次函数的性质解决日常生活中的最值问题,一般的步骤为:
①把问题归结为二次函数问题(设自变量和函数);
③在自变量的取值范围内求出最值;
②求出函数解析式(包括自变量的取值范围);
④答。
1、求下列二次函数的最大值或最小值:
y=-x2+4x
y =-(x2-4x)= =-(x2-4x+22-22)=-(x-2)2+4
所以:当x=2时,y 达到最大值为4.
解:因为 -1<0,则图像开口向下,y有最大值
当x= 时,
y达到最大值为
5.7二次函数的应用(1)
1、能分析和表示实际问题中的二次函数关系,并利用二次函数的知识解决问题。
2、能运用二次函数的性质求实际问题中的最大值或最小值
3、体会函数模型在实际问题中的应用
A
B
C
D
E
F
K
王伯伯果园里有一块边长为10米的等边三角形空地,想从上面建一个面积最大的矩形蓄水池,应怎样建才能使蓄水池的占地面积最大?
1、二次函数y=ax2+bx+c(a≠0)何时有最大值或最小值?
2、如何求二次函数的最值?
配方法
公式法
根据二次函数的图像回答问题
y=2x2+8x+13
-2
0
2
4
6
2
-4
x
y
(2)若-3≤x≤0,该函数的最大值、最小值分别为( )( )。
(3)若-4≤x≤-3,该函数的最大值、最小值分别为( )、( )。
应注意对称轴(或顶点)是否在自变量的取值范围内。
13
13
13
(-4,13)
(-2,5)
5
7
求函数的最值问题,应注意什么
(1)该函数有最( )值是( )
小
5
例1.修建有一条边靠墙的矩形菜园,不靠墙的的三边的长度之
和为60m.应怎样设计才使菜园面积最大?最大面积是多少?
解:如图设菜园的宽为x(m),面积为y(m2),则菜园的长为 (60-2 x )(m)
依题意y与x之间的函数解析式为
60-2x
y
所以,当菜园的宽为15 m时菜园面积最大。最大面积是450m2
x
x
y=x(60-2x)
=- 2x2+60x
=-2(x-15) 2 +450
∴当x=15时,y有最大值,最大值是450
例1.修建有一条边靠墙的矩形菜园,不靠墙的的三边的长度之
和为60m.应怎样设计才使菜园面积最大?最大面积是多少?
解:如图,设菜园的长为x(m),面积为y(m2),则菜园的宽为
(m)
依题意y与x之间的函数解析式为
y
所以,当菜园的长为30 m时菜园面积最大。最大面积是450m2
x
例1.修建有一条边靠墙的矩形菜园,墙长25m,不靠墙的
三边的长度之和为60m.应怎样设计才使菜园面积最大?
最大面积是多少?
解:如图,设菜园的长为x(m),面积为y(m2),则菜园的宽为
(m)
依题意y与x之间的函数解析式为
y
x
25m
x
y
o
30
450
60
25
我们是如何运用二次函数求实际问题中的最大值或最小值
首先应当求出函数解析式和自变量的取值范围,
然后通过配方变形,或利用公式求它的最大值或最小值。
注意:由此求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内 。
例2:如图,ABCD是一块边长为2 m的正方形铁板,在边AB上选取一点M,分别以AM和MB为边截取两块相邻的正方形板料。当AM的长为何值时,截取的板料面积最小?
D
2m
X
A
B
C
M
解:设AM的长为x(m),则BM的长为(2-x)m,以AM和MB为边的两块正方形面积之和为y.依题意得y与x之间的函数解析式为
所以,当AM的长为1m时,截取的板料面积最小,最小面积为2m2.
2-x
y=x2+(2-x)2
=2x2-4x+4
(2017泰安中考第20题)如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19cm2 B.16cm2
C.15cm2 D.12cm2
C
(2016年绍兴中考)用长为8米的铝合金制成如图窗框,问窗框的宽和高各多少米时,窗户的透光面积最大?最大面积是多少?
解:设矩形窗框的宽为x米, 面积为y,由题意得,
今天你学到了什么?最深的感受是什么?
实际问题
抽象转化
建立函数模型
数学问题
运用
数学知识
问题的解
返回解释
检验
王伯伯果园里有一块边长为10米的等边三角形空地,想从上面建一个面积最大的矩形蓄水池,应怎样建?才能使蓄水池的占地面积最大?
A
B
C
D
E
F
K
已知直角三角形的两直角边的和为2。求斜边长可能达到的最小值,以及当斜边长达到最小值时两条直角边的长分别为多少?
A
B
C
2 如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,点P从点A开始沿AB边向点B以2厘米/秒的速度移动,点Q从点B开始沿BC边向点C以1厘米/秒的速度移动,如果P,Q分别
从A,B同时出发,几秒后
ΔPBQ的面积最大?
最大面积是多少?
A
B
C
P
Q
解:根据题意,设经过x秒后ΔPBQ的面积y最大,则:
AP=2x cm PB=(8-2x ) cm
QB=x cm
则 y=1/2 x(8-2x)
=-x2 +4x
=-(x2 -4x +4 -4)
= -(x - 2)2 + 4
所以,当P、Q同时运动2秒后ΔPBQ的面积y最大
最大面积是 4 cm2
(0
B
C
P
Q
问题5:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
A
B
C
D
解:
(1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
(2)当x= 时,S最大值= =36(平方米)
∴ S=x(24-4x)
=-4x2+24 x (0
∴当x=4m时,S最大值=32 平方米
2、用长为8米的铝合金制成如图窗框,一边靠2m的墙问窗框的宽和高各为多少米时,窗户的透光面积最大?最大面积是多少?
解:设窗框的一边长为x米,
x
又令该窗框的透光面积为y米,那么:
y= x
即:y=-0.5x2+4x
则另一边的长为 米,
小试牛刀
x
y
o
4
48
8
挑战自我
如图,用篱笆围成一个一面靠墙(墙的最大可用长度为10m)、中间隔着一道篱笆的矩形菜园.已知篱笆的长度为24m.设菜园的宽AB为x(m),面积为y(m ).
(1)写出y与x之间的函数表达式及自变量的取值范围;
(2)围成的菜园的最大面积是多少?这时菜园的宽x等于多少?
A
D
B
C
10
y= -3x +24x
当x=4时,y大=48
当x= 时,y大=
x
y
o
12
48
24
挑战自我
如图,用篱笆围成一个一面靠墙(墙的最大可用长度为10m)、中间隔着一道篱笆的矩形菜园.已知篱笆的长度为24m.设菜园的宽AB为x(m),面积为y(m ).
(1)写出y与x之间的函数表达式及自变量的取值范围;
(2)围成的菜园的最大面积是多少?这时菜园的宽x等于多少?
A
D
B
C
10
x
y
10
当x=10 时,y大=
小结:应用二次函数的性质解决日常生活中的最值问题,一般的步骤为:
①把问题归结为二次函数问题(设自变量和函数);
③在自变量的取值范围内求出最值;
②求出函数解析式(包括自变量的取值范围);
④答。
1、求下列二次函数的最大值或最小值:
y=-x2+4x
y =-(x2-4x)= =-(x2-4x+22-22)=-(x-2)2+4
所以:当x=2时,y 达到最大值为4.
解:因为 -1<0,则图像开口向下,y有最大值
当x= 时,
y达到最大值为
