青岛版九年级数学下册 5.7二次函数的应用 第二课时 课件(共15张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 5.7二次函数的应用 第二课时 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 804.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 09:05:38 | ||
图片预览





文档简介
(共15张PPT)
5.7 二次函数的应用
第二课时
知识回顾
利用二次函数解应用题的一般步骤:
1.设未知数(确定自变量和函数);
2.找等量关系,列出函数关系式;
3.化简,整理成标准形式(一次函数、二次函数等);
4.求自变量取值范围;
5.利用函数知识,求解(通常是最值问题);
6.写出结论.
例3:运动员掷一枚铅球,铅球抛出时离地面的高度为5/3m,抛出后,铅球行进的路线是一抛物线,行进时里离地面的最大高度是3m,此时铅球沿水平方向行进了4m.求铅球从抛出到落在地面走过的水平距离?
例题讲解
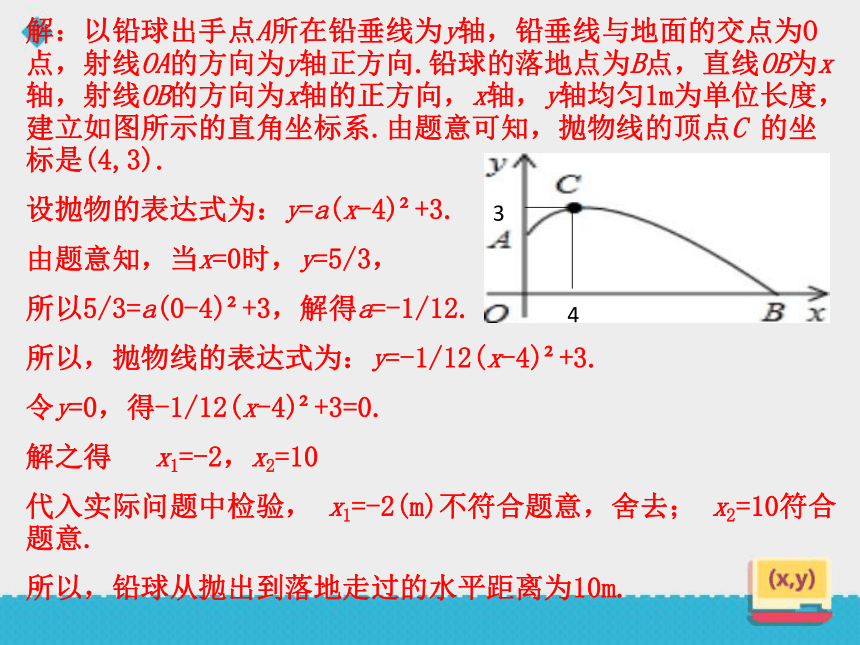
解:以铅球出手点A所在铅垂线为y轴,铅垂线与地面的交点为O点,射线OA的方向为y轴正方向.铅球的落地点为B点,直线OB为x轴,射线OB的方向为x轴的正方向,x轴,y轴均匀1m为单位长度,建立如图所示的直角坐标系.由题意可知,抛物线的顶点C 的坐标是(4,3).
设抛物的表达式为:y=a(x-4) +3.
由题意知,当x=0时,y=5/3,
所以5/3=a(0-4) +3,解得a=-1/12.
所以,抛物线的表达式为:y=-1/12(x-4) +3.
令y=0,得-1/12(x-4) +3=0.
解之得 x1=-2,x2=10
代入实际问题中检验, x1=-2(m)不符合题意,舍去; x2=10符合题意.
所以,铅球从抛出到落地走过的水平距离为10m.
4
3
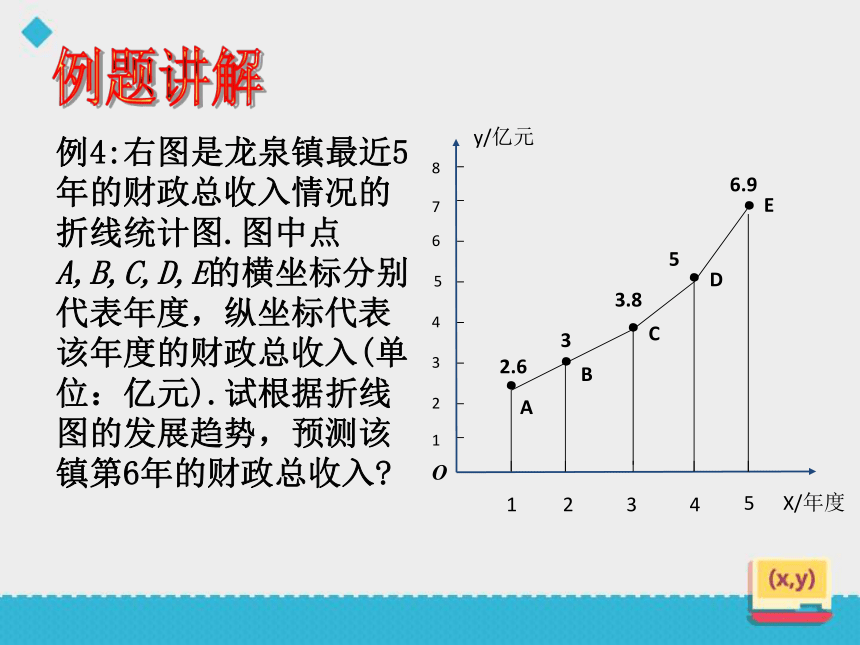
例4:右图是龙泉镇最近5年的财政总收入情况的折线统计图.图中点A,B,C,D,E的横坐标分别代表年度,纵坐标代表该年度的财政总收入(单位:亿元).试根据折线图的发展趋势,预测该镇第6年的财政总收入
y/亿元
O
X/年度
2
4
1
3
1
2
3
4
5
6
7
8
﹒
5
﹒
﹒
﹒
﹒
A
B
C
D
E
2.6
3
3.8
5
6.9
例题讲解
方法点拨
由上图可以看出A,B,C,D,E近似的分布在一条抛物线上,因此可以选取其中的三个点,求出有这三个点确定的抛物线的解析式,然后验证其他各点是否也靠近这条抛物线,如果靠近,便可推测第6年的财政总收入也符合以上规律.从而可以预测第6年的财政总收入.
解:设图像过A,C,D三点的二次函数表达式为y=ax +bx+c.将这三点的坐标(1,2.6)(3,3.8)(4,5)分别代入上式,得
2.6=a×1 +b×1+c
3.8=a×3 +b×3+c
5=a×4 +b×4+c
解得 a=0.2
b=-0.2
c=2.6
所以,经过A,C,D三点的二次函数的表达式为
y=0.2x -0.2x+2.6
当x=2时,代入y=0.2x -0.2x+2.6,得y=3,与B点纵坐标相等,这说明点B在经过A,C,D三点的二次函数的图像上,即这条抛物线上相应的点的纵坐标反映了该镇第2年的财政收入.当x=5时,代入y=0.2x -0.2x+2.6,得y=6.6,E点纵坐标为6.9,相差0.3(亿元),这说明点E虽不在经过A,C,D三点的抛物线上,但比较接近,即这条抛物线上相应的点的纵坐标可以近似的反映该镇第5年的财政收入.由此可知,二次函数y=0.2x -0.2x+2.6可以近似的反映该镇最近5年的财政收入情况发展趋势,因此可以利用前5年的发展趋势预测第6年的财政收入.
当x=6时,代入y=0.2x -0.2x+2.6,得x=8.6,所以,可以预测2010年该镇的财政收入约为8.6亿元.
y/亿元
O
X/年度
2
4
1
3
1
2
3
4
5
6
7
8
5
A
B
C
D
E
2.6
3
3.8
5
6.9
1、恰当的建立平面直角坐标系,构造出符合题意的二次函数(一次函数、反比例函数)是解决此类问题的关键.
2、此类问题进一步体现了数学建模思想方法的应用,同学们要认真掌握!
归纳:
1.如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,
求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;
(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
当堂检测
1. 解:(1)设所求函数的解析式为y=ax2.
由题意,得函数图象经过点B(3,-5),
∴-5=9a.
∴ .
∴所求的二次函数的解析式为 .
x的取值范围是-3≤x≤3;
(2)当车宽2.8米时,此时CN为1.4米,
对应 ,
EN长为5- = ,车高 米,
∵ >1,
∴农用货车能够通过此隧道.
2.如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线 的一部分.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
当堂检测
2.解: (1)
∵ ,
∴函数的最大值是
答:演员弹跳的最大高度是 米.
(2) ,
所以这次表演成功.
当堂检测
课堂小结
本节课利用二次函数建立数学模型,并利用二次函数的有关性质来解决实际问题.
作 业
课本
P.55 第1题
5.7 二次函数的应用
第二课时
知识回顾
利用二次函数解应用题的一般步骤:
1.设未知数(确定自变量和函数);
2.找等量关系,列出函数关系式;
3.化简,整理成标准形式(一次函数、二次函数等);
4.求自变量取值范围;
5.利用函数知识,求解(通常是最值问题);
6.写出结论.
例3:运动员掷一枚铅球,铅球抛出时离地面的高度为5/3m,抛出后,铅球行进的路线是一抛物线,行进时里离地面的最大高度是3m,此时铅球沿水平方向行进了4m.求铅球从抛出到落在地面走过的水平距离?
例题讲解
解:以铅球出手点A所在铅垂线为y轴,铅垂线与地面的交点为O点,射线OA的方向为y轴正方向.铅球的落地点为B点,直线OB为x轴,射线OB的方向为x轴的正方向,x轴,y轴均匀1m为单位长度,建立如图所示的直角坐标系.由题意可知,抛物线的顶点C 的坐标是(4,3).
设抛物的表达式为:y=a(x-4) +3.
由题意知,当x=0时,y=5/3,
所以5/3=a(0-4) +3,解得a=-1/12.
所以,抛物线的表达式为:y=-1/12(x-4) +3.
令y=0,得-1/12(x-4) +3=0.
解之得 x1=-2,x2=10
代入实际问题中检验, x1=-2(m)不符合题意,舍去; x2=10符合题意.
所以,铅球从抛出到落地走过的水平距离为10m.
4
3
例4:右图是龙泉镇最近5年的财政总收入情况的折线统计图.图中点A,B,C,D,E的横坐标分别代表年度,纵坐标代表该年度的财政总收入(单位:亿元).试根据折线图的发展趋势,预测该镇第6年的财政总收入
y/亿元
O
X/年度
2
4
1
3
1
2
3
4
5
6
7
8
﹒
5
﹒
﹒
﹒
﹒
A
B
C
D
E
2.6
3
3.8
5
6.9
例题讲解
方法点拨
由上图可以看出A,B,C,D,E近似的分布在一条抛物线上,因此可以选取其中的三个点,求出有这三个点确定的抛物线的解析式,然后验证其他各点是否也靠近这条抛物线,如果靠近,便可推测第6年的财政总收入也符合以上规律.从而可以预测第6年的财政总收入.
解:设图像过A,C,D三点的二次函数表达式为y=ax +bx+c.将这三点的坐标(1,2.6)(3,3.8)(4,5)分别代入上式,得
2.6=a×1 +b×1+c
3.8=a×3 +b×3+c
5=a×4 +b×4+c
解得 a=0.2
b=-0.2
c=2.6
所以,经过A,C,D三点的二次函数的表达式为
y=0.2x -0.2x+2.6
当x=2时,代入y=0.2x -0.2x+2.6,得y=3,与B点纵坐标相等,这说明点B在经过A,C,D三点的二次函数的图像上,即这条抛物线上相应的点的纵坐标反映了该镇第2年的财政收入.当x=5时,代入y=0.2x -0.2x+2.6,得y=6.6,E点纵坐标为6.9,相差0.3(亿元),这说明点E虽不在经过A,C,D三点的抛物线上,但比较接近,即这条抛物线上相应的点的纵坐标可以近似的反映该镇第5年的财政收入.由此可知,二次函数y=0.2x -0.2x+2.6可以近似的反映该镇最近5年的财政收入情况发展趋势,因此可以利用前5年的发展趋势预测第6年的财政收入.
当x=6时,代入y=0.2x -0.2x+2.6,得x=8.6,所以,可以预测2010年该镇的财政收入约为8.6亿元.
y/亿元
O
X/年度
2
4
1
3
1
2
3
4
5
6
7
8
5
A
B
C
D
E
2.6
3
3.8
5
6.9
1、恰当的建立平面直角坐标系,构造出符合题意的二次函数(一次函数、反比例函数)是解决此类问题的关键.
2、此类问题进一步体现了数学建模思想方法的应用,同学们要认真掌握!
归纳:
1.如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,
求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;
(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
当堂检测
1. 解:(1)设所求函数的解析式为y=ax2.
由题意,得函数图象经过点B(3,-5),
∴-5=9a.
∴ .
∴所求的二次函数的解析式为 .
x的取值范围是-3≤x≤3;
(2)当车宽2.8米时,此时CN为1.4米,
对应 ,
EN长为5- = ,车高 米,
∵ >1,
∴农用货车能够通过此隧道.
2.如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线 的一部分.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
当堂检测
2.解: (1)
∵ ,
∴函数的最大值是
答:演员弹跳的最大高度是 米.
(2) ,
所以这次表演成功.
当堂检测
课堂小结
本节课利用二次函数建立数学模型,并利用二次函数的有关性质来解决实际问题.
作 业
课本
P.55 第1题
