青岛版九年级数学下册 5.2反比例函数 第3课时 (共17张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 5.2反比例函数 第3课时 (共17张PPT) | 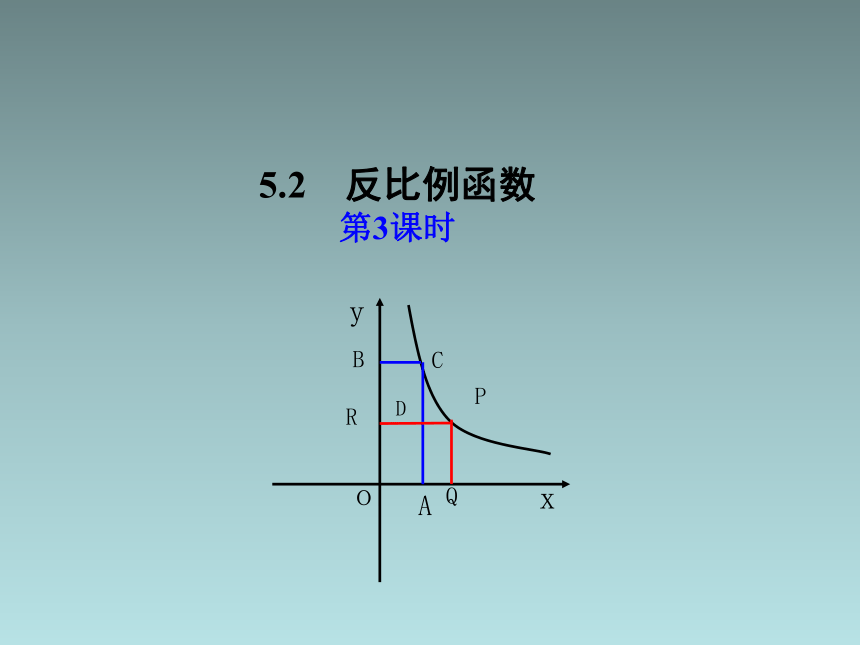 | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 09:32:01 | ||
图片预览



文档简介
(共17张PPT)
5.2 反比例函数
第3课时
C
o
y
x
P
R
B
D
A
Q
1.进一步理解和掌握反比例函数及其图象与性质;
2.能灵活运用函数图象和性质解决一些较综合的问题; 3.反比例函数的比例系数k的几何意义:∣k∣是过双曲线上 任意一点分别向两坐标轴作垂线段与轴围成的矩形面积;
4.深刻领会函数解析式与函数图象之间的联系,体会数形结合及转化的思想方法.
反比例函数图象性质是什么?
绘制反比例函数图象的步骤是什么?
回顾思考
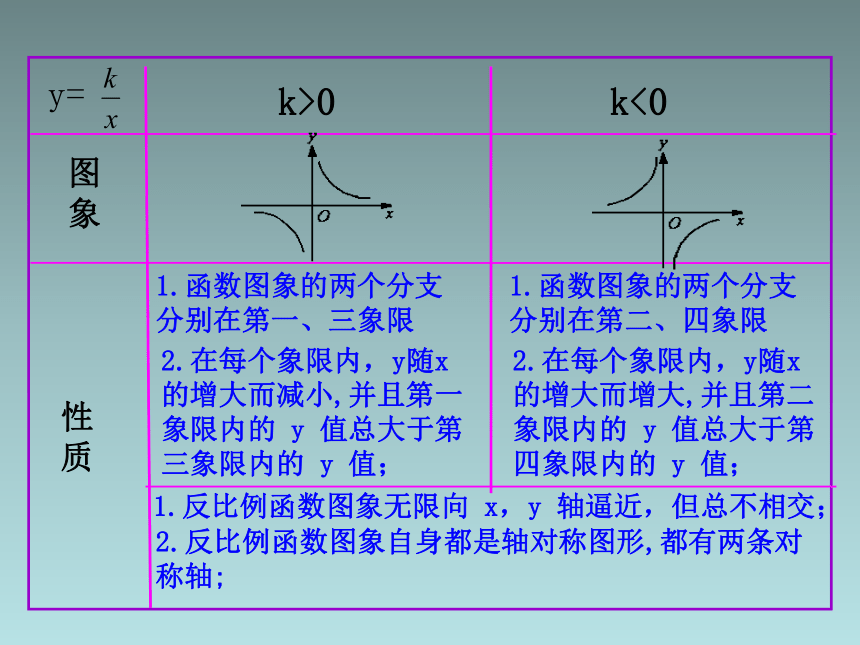
k>0
k<0
1.函数图象的两个分支
分别在第一、三象限
图
象
性质
y=
2.在每个象限内,y随x的增大而减小,并且第一象限内的 y 值总大于第三象限内的 y 值;
1.函数图象的两个分支
分别在第二、四象限
2.在每个象限内,y随x的增大而增大,并且第二象限内的 y 值总大于第四象限内的 y 值;
2.反比例函数图象自身都是轴对称图形,都有两条对称轴;
1.反比例函数图象无限向 x,y 轴逼近,但总不相交;
函数图象画法
连
线
列
表
描
点
描点法
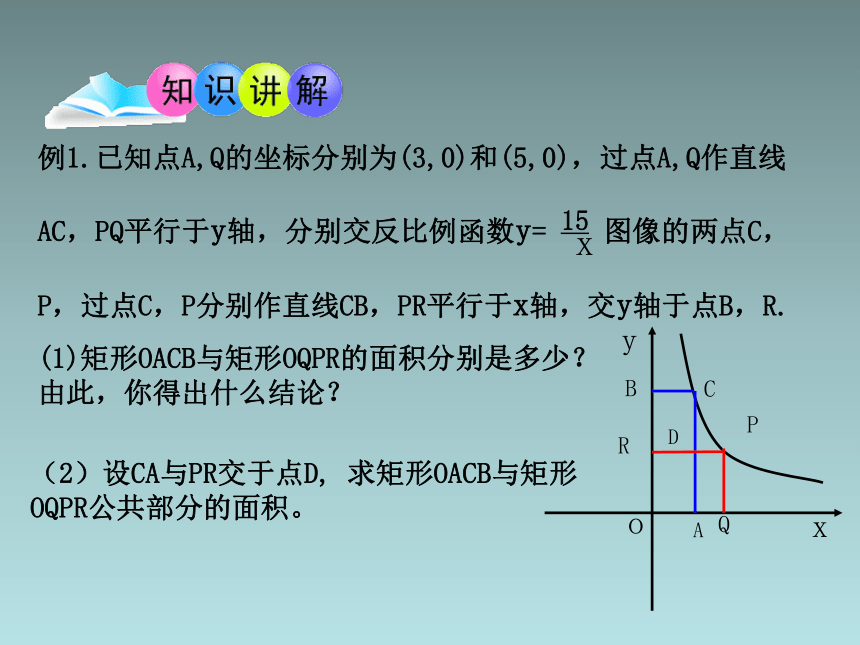
例1.已知点A,Q的坐标分别为(3,0)和(5,0),过点A,Q作直线
AC,PQ平行于y轴,分别交反比例函数y= 15 图像的两点C,
P,过点C,P分别作直线CB,PR平行于x轴,交y轴于点B,R.
(2)设CA与PR交于点D, 求矩形OACB与矩形OQPR公共部分的面积。
(1)矩形OACB与矩形OQPR的面积分别是多少?
由此,你得出什么结论?
C
o
y
x
P
R
B
D
A
Q
x
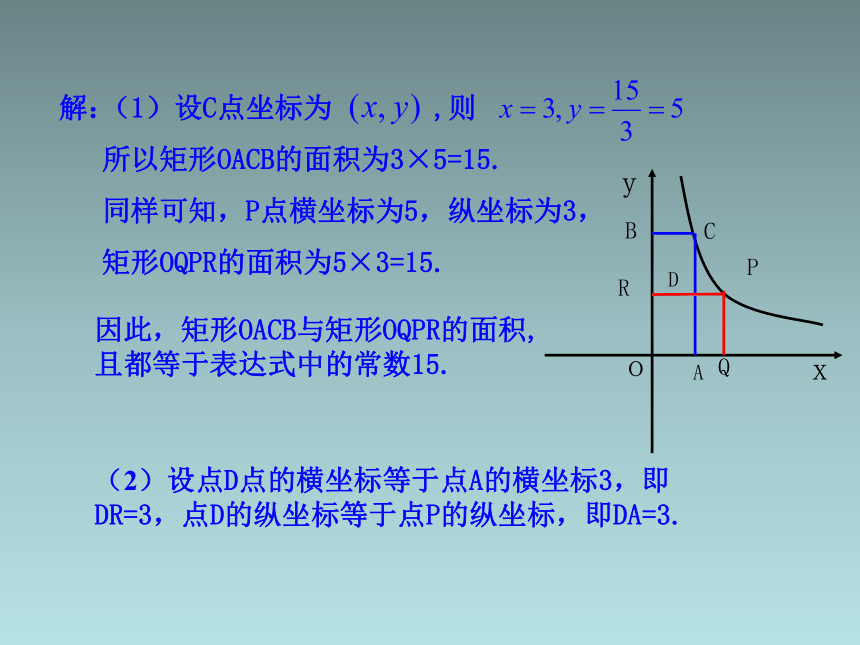
(2)设点D点的横坐标等于点A的横坐标3,即 DR=3,点D的纵坐标等于点P的纵坐标,即DA=3.
因此,矩形OACB与矩形OQPR的面积,
且都等于表达式中的常数15.
(1)设C点坐标为 ,则
所以矩形OACB的面积为3×5=15.
同样可知,P点横坐标为5,纵坐标为3,
矩形OQPR的面积为5×3=15.
解:
C
o
y
x
P
R
B
D
A
Q
反比例函数的比例系数k的几何意义: ∣k∣是过双曲线上任意一点分别向两坐标轴作垂线段与轴围成的矩形面积.
一般的,从反比例函数y= k 图象上任意一点P,向x轴和y轴作垂线,由点P与两个垂足及坐标原点形成的矩形面积等于常数∣k∣.
x
A
o
y
x
B
S1
S2
如图,A,B是双曲线 上的点,分别经过A,B两点向x轴、y轴作垂线段,若 .
4
例2.如图,已知在平面直角坐标系中,点A(2,5)在反比例
函数 的图象上,过点A的直线 交x轴于点B.
(1)求k和b的值;
(2)求△OAB的面积.
.
解:(1)把A(2,5)分别代入 和 y=x+b,
得,
解得k=10,b=3;
(0≤x≤ 5)
2+b=5 (5<x≤15)
(2)作AC ⊥ x轴与点C,, 由(1)得直线AB的解析式为y=x+3, ∴点B的坐标为(-3,0), OB=3, 点A的坐标是(2,5), ∴AC=5,
1.如图,点P是反比例函数图象上的一点,过点P分别向
x轴、y轴作垂线,若阴影部分面积为1,则这个反比例
函数的关系式是 .
P
y
x
O
C
x
y
2
-
=
A
y
O
B
x
A
y
O
B
x
M
N
C
D
A
y
O
B
x
M
N
C
D
反比例函数的比例系数k的几何意义:
∣k∣是过双曲线上任意一点分别向两坐标轴作垂线段与轴围成的矩形面积.
5.2 反比例函数
第3课时
C
o
y
x
P
R
B
D
A
Q
1.进一步理解和掌握反比例函数及其图象与性质;
2.能灵活运用函数图象和性质解决一些较综合的问题; 3.反比例函数的比例系数k的几何意义:∣k∣是过双曲线上 任意一点分别向两坐标轴作垂线段与轴围成的矩形面积;
4.深刻领会函数解析式与函数图象之间的联系,体会数形结合及转化的思想方法.
反比例函数图象性质是什么?
绘制反比例函数图象的步骤是什么?
回顾思考
k>0
k<0
1.函数图象的两个分支
分别在第一、三象限
图
象
性质
y=
2.在每个象限内,y随x的增大而减小,并且第一象限内的 y 值总大于第三象限内的 y 值;
1.函数图象的两个分支
分别在第二、四象限
2.在每个象限内,y随x的增大而增大,并且第二象限内的 y 值总大于第四象限内的 y 值;
2.反比例函数图象自身都是轴对称图形,都有两条对称轴;
1.反比例函数图象无限向 x,y 轴逼近,但总不相交;
函数图象画法
连
线
列
表
描
点
描点法
例1.已知点A,Q的坐标分别为(3,0)和(5,0),过点A,Q作直线
AC,PQ平行于y轴,分别交反比例函数y= 15 图像的两点C,
P,过点C,P分别作直线CB,PR平行于x轴,交y轴于点B,R.
(2)设CA与PR交于点D, 求矩形OACB与矩形OQPR公共部分的面积。
(1)矩形OACB与矩形OQPR的面积分别是多少?
由此,你得出什么结论?
C
o
y
x
P
R
B
D
A
Q
x
(2)设点D点的横坐标等于点A的横坐标3,即 DR=3,点D的纵坐标等于点P的纵坐标,即DA=3.
因此,矩形OACB与矩形OQPR的面积,
且都等于表达式中的常数15.
(1)设C点坐标为 ,则
所以矩形OACB的面积为3×5=15.
同样可知,P点横坐标为5,纵坐标为3,
矩形OQPR的面积为5×3=15.
解:
C
o
y
x
P
R
B
D
A
Q
反比例函数的比例系数k的几何意义: ∣k∣是过双曲线上任意一点分别向两坐标轴作垂线段与轴围成的矩形面积.
一般的,从反比例函数y= k 图象上任意一点P,向x轴和y轴作垂线,由点P与两个垂足及坐标原点形成的矩形面积等于常数∣k∣.
x
A
o
y
x
B
S1
S2
如图,A,B是双曲线 上的点,分别经过A,B两点向x轴、y轴作垂线段,若 .
4
例2.如图,已知在平面直角坐标系中,点A(2,5)在反比例
函数 的图象上,过点A的直线 交x轴于点B.
(1)求k和b的值;
(2)求△OAB的面积.
.
解:(1)把A(2,5)分别代入 和 y=x+b,
得,
解得k=10,b=3;
(0≤x≤ 5)
2+b=5 (5<x≤15)
(2)作AC ⊥ x轴与点C,, 由(1)得直线AB的解析式为y=x+3, ∴点B的坐标为(-3,0), OB=3, 点A的坐标是(2,5), ∴AC=5,
1.如图,点P是反比例函数图象上的一点,过点P分别向
x轴、y轴作垂线,若阴影部分面积为1,则这个反比例
函数的关系式是 .
P
y
x
O
C
x
y
2
-
=
A
y
O
B
x
A
y
O
B
x
M
N
C
D
A
y
O
B
x
M
N
C
D
反比例函数的比例系数k的几何意义:
∣k∣是过双曲线上任意一点分别向两坐标轴作垂线段与轴围成的矩形面积.
