2021—2022学年鲁教版(五四制)数学六年级下册6.5.3整式的乘法---多项式乘以多项式-导学案(表格式、无答案)
文档属性
| 名称 | 2021—2022学年鲁教版(五四制)数学六年级下册6.5.3整式的乘法---多项式乘以多项式-导学案(表格式、无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 156.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 16:02:51 | ||
图片预览

文档简介
课 题 多项式乘以多项式 课 型 新授课 年 级 六年级
主备人 审核人 讲学时间
学习目标 1、掌握多项式乘多项式的法则,并应用进行计算 2、通过法则的探究过程,进一步体验转化的数学思想 3、经过动手计算,训练自己认真审题、计算的习惯 4.渗透公式恒等变形的和谐美、简洁美.
重点 多项式乘多项式的法则应用
难点 体会转化的思想方法及法则的符号确定
课前准备 多媒体
学习过程
学生自主活动材料
复习回顾 计算:(1)-2x2.3xy2 (2)-2x(1-x)(3)x(4x2+x)(4) 单项式乘乘以单项式法则:单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。单项式乘以多项式法则:单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。
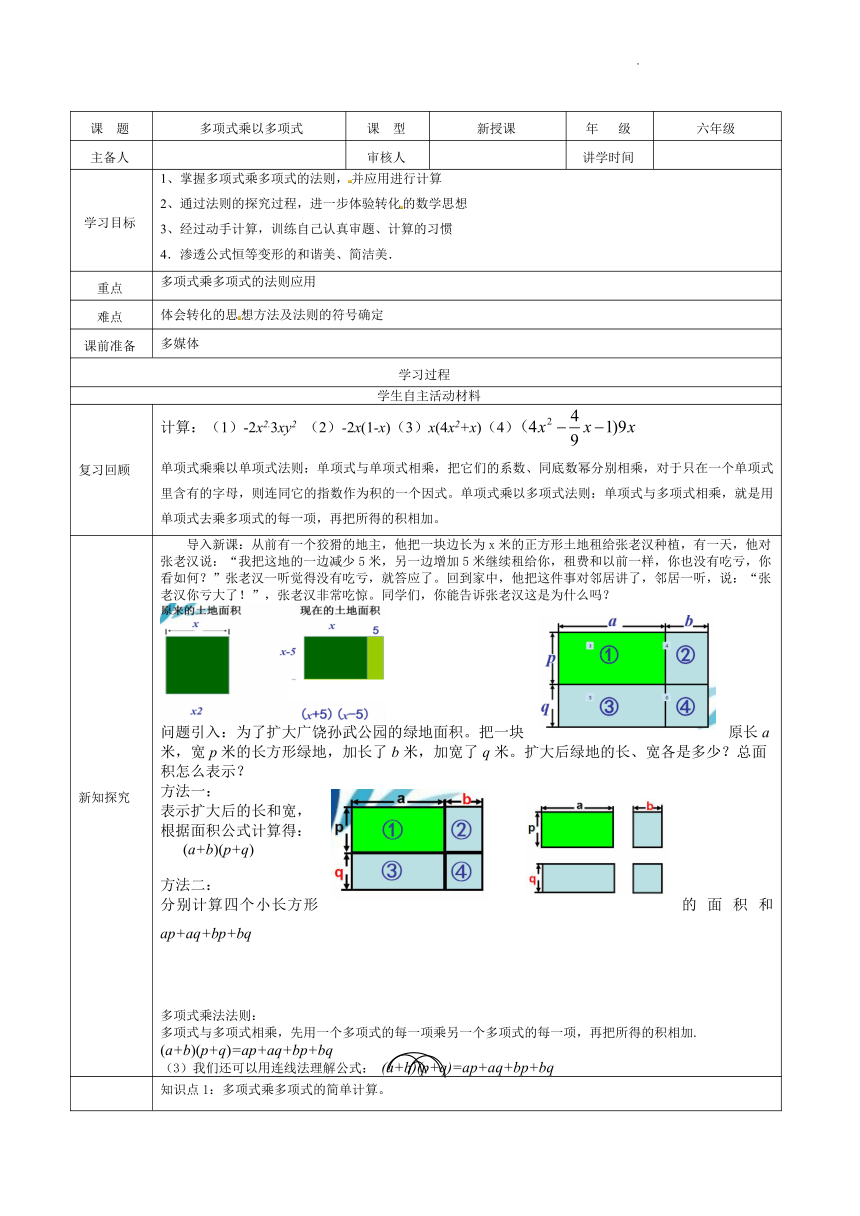
新知探究 导入新课:从前有一个狡猾的地主,他把一块边长为x米的正方形土地租给张老汉种植,有一天,他对张老汉说:“我把这地的一边减少5米,另一边增加5米继续租给你,租费和以前一样,你也没有吃亏,你看如何?”张老汉一听觉得没有吃亏,就答应了。回到家中,他把这件事对邻居讲了,邻居一听,说:“张老汉你亏大了!”,张老汉非常吃惊。同学们,你能告诉张老汉这是为什么吗? 问题引入:为了扩大广饶孙武公园的绿地面积。把一块原长a米,宽p米的长方形绿地,加长了b米,加宽了q米。扩大后绿地的长、宽各是多少?总面积怎么表示? 方法一: 表示扩大后的长和宽, 根据面积公式计算得: (a+b)(p+q) 方法二: 分别计算四个小长方形的面积和ap+aq+bp+bq 多项式乘法法则: 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加. (a+b)(p+q)=ap+aq+bp+bq (3)我们还可以用连线法理解公式: (a+b)(p+q)=ap+aq+bp+bq
典型例题 知识点1:多项式乘多项式的简单计算。 【例1】计算:⑴ (1-x)(0.6-x) ⑵(-2m-1)(3m-2) 【解题提示】利用多项式乘多项式的法则进行计算时,注意不要漏乘,同时注意符号的变化。 解: 知识点2:多项式乘多项式的简单应用 【例2】1.先化简后求值 (2a-3)(3a+1)-6a(a-4) a= 2.若多项式5x2+2x-3与多项式mx+2的乘积不含x的二次项,求m的值.
巩固练习 (2x+1)(x+3) (2n+5)(n-3) 3.(a-1)24.(a+3b)(a-3b)
课后作业 必做题:课本40页习题6.10 第1题 选做题:课本40页习题6.10 第4题
评价专栏(分优良中差四个等级)
【自我评价专栏】合作与交流: 书写: 综合:
【组员评价专栏】合作与交流: 书写: 综合:
主备人 审核人 讲学时间
学习目标 1、掌握多项式乘多项式的法则,并应用进行计算 2、通过法则的探究过程,进一步体验转化的数学思想 3、经过动手计算,训练自己认真审题、计算的习惯 4.渗透公式恒等变形的和谐美、简洁美.
重点 多项式乘多项式的法则应用
难点 体会转化的思想方法及法则的符号确定
课前准备 多媒体
学习过程
学生自主活动材料
复习回顾 计算:(1)-2x2.3xy2 (2)-2x(1-x)(3)x(4x2+x)(4) 单项式乘乘以单项式法则:单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。单项式乘以多项式法则:单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。
新知探究 导入新课:从前有一个狡猾的地主,他把一块边长为x米的正方形土地租给张老汉种植,有一天,他对张老汉说:“我把这地的一边减少5米,另一边增加5米继续租给你,租费和以前一样,你也没有吃亏,你看如何?”张老汉一听觉得没有吃亏,就答应了。回到家中,他把这件事对邻居讲了,邻居一听,说:“张老汉你亏大了!”,张老汉非常吃惊。同学们,你能告诉张老汉这是为什么吗? 问题引入:为了扩大广饶孙武公园的绿地面积。把一块原长a米,宽p米的长方形绿地,加长了b米,加宽了q米。扩大后绿地的长、宽各是多少?总面积怎么表示? 方法一: 表示扩大后的长和宽, 根据面积公式计算得: (a+b)(p+q) 方法二: 分别计算四个小长方形的面积和ap+aq+bp+bq 多项式乘法法则: 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加. (a+b)(p+q)=ap+aq+bp+bq (3)我们还可以用连线法理解公式: (a+b)(p+q)=ap+aq+bp+bq
典型例题 知识点1:多项式乘多项式的简单计算。 【例1】计算:⑴ (1-x)(0.6-x) ⑵(-2m-1)(3m-2) 【解题提示】利用多项式乘多项式的法则进行计算时,注意不要漏乘,同时注意符号的变化。 解: 知识点2:多项式乘多项式的简单应用 【例2】1.先化简后求值 (2a-3)(3a+1)-6a(a-4) a= 2.若多项式5x2+2x-3与多项式mx+2的乘积不含x的二次项,求m的值.
巩固练习 (2x+1)(x+3) (2n+5)(n-3) 3.(a-1)24.(a+3b)(a-3b)
课后作业 必做题:课本40页习题6.10 第1题 选做题:课本40页习题6.10 第4题
评价专栏(分优良中差四个等级)
【自我评价专栏】合作与交流: 书写: 综合:
【组员评价专栏】合作与交流: 书写: 综合:
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
