高中数学人教A版(2019)必修第二册 8.1基本立体图形 学案
文档属性
| 名称 | 高中数学人教A版(2019)必修第二册 8.1基本立体图形 学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 757.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 20:19:54 | ||
图片预览



文档简介
8.1 基本立体图形
知识梳理
1、空间几何体
(1)空间中的物体都占据着空间的一部分,若只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.
(2)多面体
由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点.
2、棱柱、棱锥、棱台的概念
多面体 定义 图形及表示 相关概念
棱柱 有两个互相平行,其余各面都是平行四边形,并且每相邻两个四边形的公共边都相互平行,由这些边所围成的多面体叫做棱柱 如图可记作:棱柱AC′或
ABCD A′B′C′D′ 底面(底):两个相互平行的面 侧面:其余各面 侧棱:相邻侧面的公共边 顶点:侧面与底面的公共顶点
棱锥 有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫棱锥 如图可记作:棱锥SABCD 底面(底):多边形面. 侧面:有公共顶点的各个三角形 侧棱:相邻侧面的公共边 顶点:各侧面的公共顶点.
棱台 用一个平行于底面的平面去截棱锥,底面与截面之间的部分叫做棱台 如图可记作:棱台ABCDA′B′C′D′ 上底面:原棱锥的截面 下底面:原棱锥的底面 侧面:其余各面.侧棱:相邻侧面的公共边.顶点:侧面与上(下)底面的公共顶点
3、棱柱、棱锥、棱台的分类
(1)棱柱的分类
①按底面多边形的边数分类.
(
n
变形
)
②按侧棱与底面是否垂直分类.
(2)棱锥的分类(棱台分类)
①按底面多边形的边数分类.
三棱锥、四棱锥、五棱锥等.
②按底面多边形是否为正多边形分类.
正棱锥和一般棱锥.
4、旋转体
由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体,这条定直线叫做旋转体的轴.
5、圆柱、圆锥、圆台的概念
旋转体 结构特征 图示 表示法
圆柱 以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱.旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;无论旋转到什么位置,不垂直于轴边都叫做圆柱侧面的母线。圆柱和棱柱统称为柱体 圆柱用表示它的轴的字母表示,左图中圆柱表示为圆柱O′O
圆锥 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥.棱锥与圆锥统称为椎体 圆锥用表示它的轴的字母表示,左图中圆锥表示为 圆 锥SO
圆台 用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.与圆柱和圆锥一样,圆台也有轴、底面、侧面、母线.棱台与圆台统称为台体 圆台用表示它的轴的字母表示,左图中圆台表示为圆台O′O
6、球的概念
旋转体 结构特征 图示 表示法
球 以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球;半圆的圆心叫做球的球心;半圆的半径叫做球的半径;半圆的直径叫做球的直径 球常用表示球心的字母O表示,左图中的球表示为球O
7、简单组合体的结构特征.
(1)由简单几何体组合而成的几何体叫做简单组合体.
(2)简单组合体的两种基本形式:
简单组合体
知识典例
题型一 常见几何体的特征
例 1 观察图中的物体,说出它们的主要结构特征.
【答案】详见解析
【分析】
根据实物图抽象出几何图形,结合几何图形的特征进行识别.
【详解】
(1)圆台,它可看作用平行于圆锥底面的平面截圆锥,截面与底面之间的部分;
(2)圆柱,它可看作矩形绕其一边旋转一周,其余三边形成的面围成的几何体;
(3)球,它可看作半圆绕直径所在直线旋转一周,半圆形成的曲面围成的几何体;
(4)圆锥,它可看作由一个直角三角形绕其一条直角边所在直线旋转一周,另一条直角边和斜边形成的面围成的几何体.
巩固练习
说出图中物体的主要结构特征.
【答案】详见解析
【分析】
根据实物图抽象出几何图形,结合几何图形描述结构特征.
【详解】
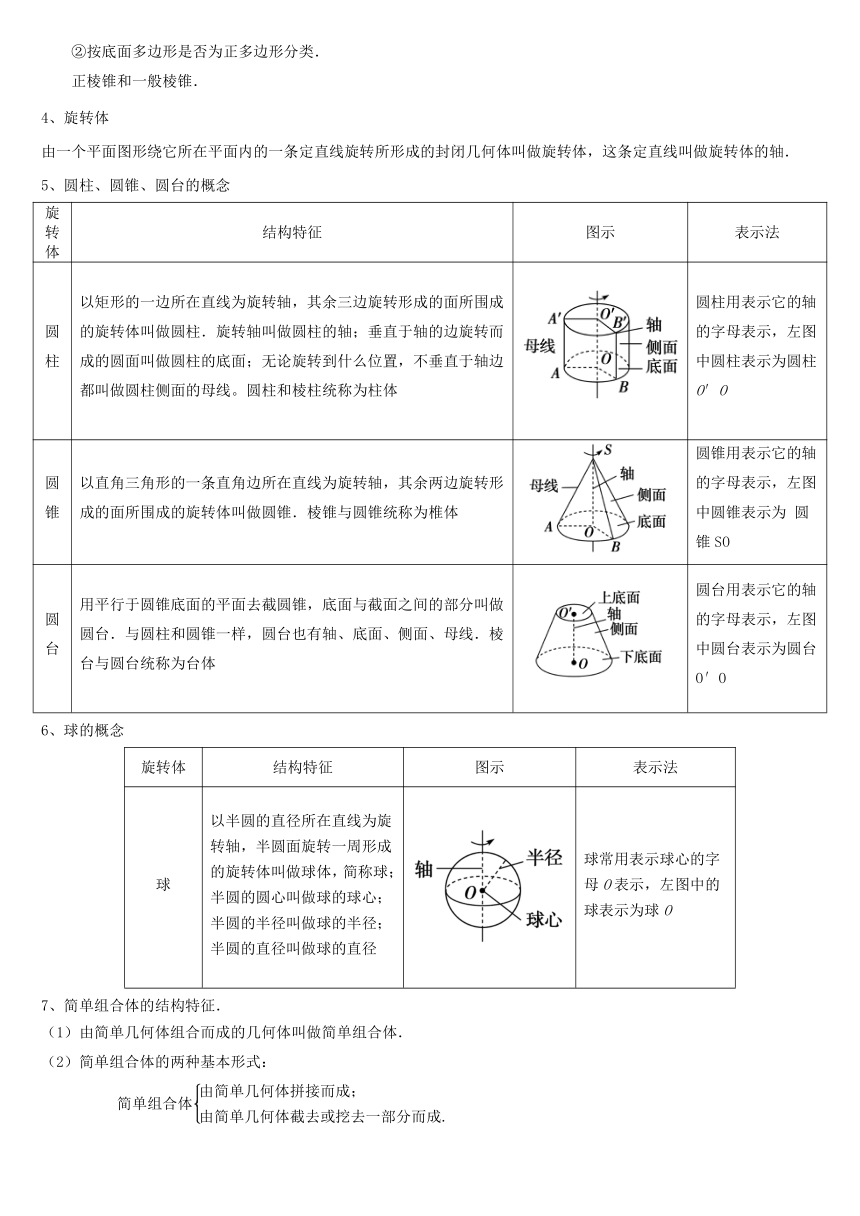
(1)一个圆柱与一个圆锥的组合体,上部分为圆锥,下部分为圆柱;
(2)一个六棱柱里面挖去了一个圆柱.
题型二 棱柱的定义及几何特征
例 2 下列说法正确的是______(填序号).
①有两个面互相平行,其余各面都是四边形的几何体是棱柱;
②有两个面互相平行,其余各面都是平行四边形的几何体是棱柱;
③有一个面是多边形,其余各面都是三角形的几何体是棱锥;
④用一个平面去截棱锥,棱锥底面和截面之间那部分的几何体是棱台;
⑤存在一个四棱锥,其四个侧面都是直角三角形.
【答案】⑤
【分析】
根据棱柱、棱锥、棱台的定义判断①②③④,再举一例说明⑤正确.
【详解】
对于①,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,故①不正确;
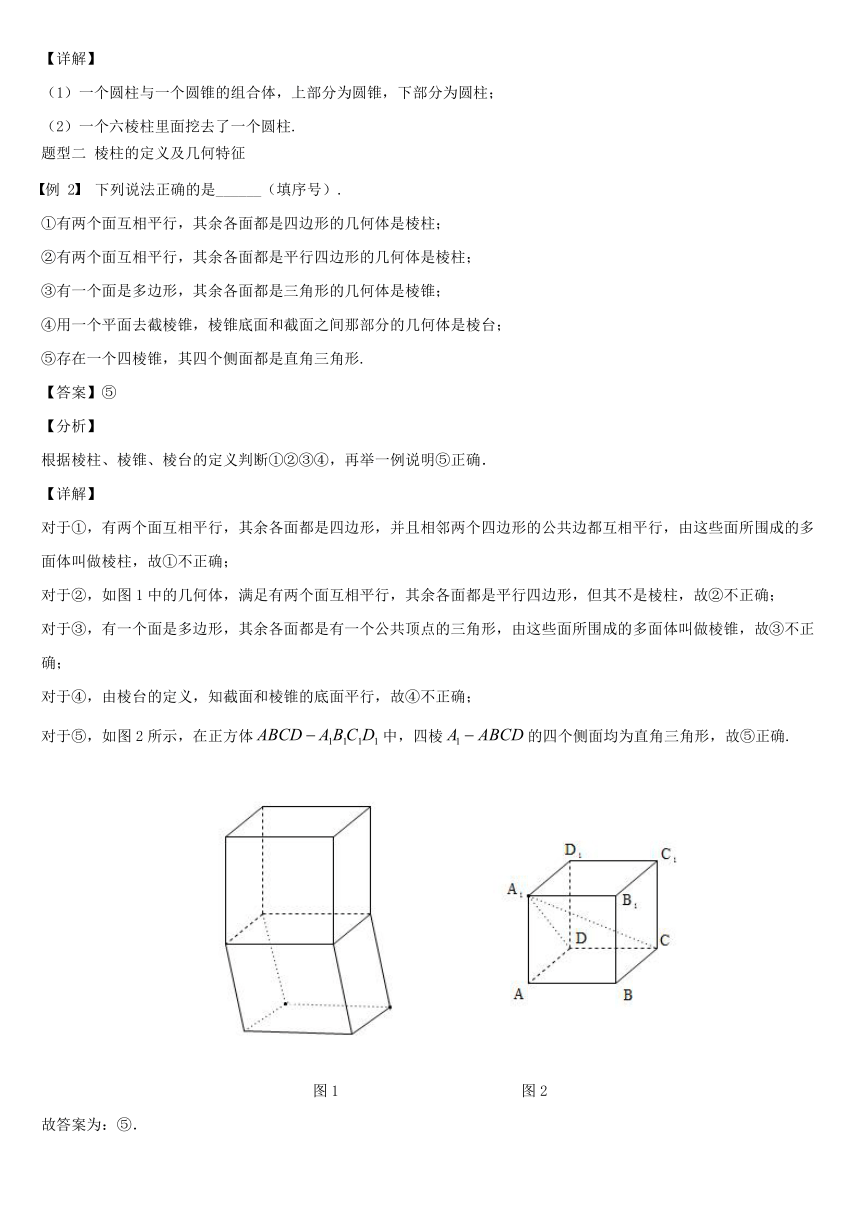
对于②,如图1中的几何体,满足有两个面互相平行,其余各面都是平行四边形,但其不是棱柱,故②不正确;
对于③,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥,故③不正确;
对于④,由棱台的定义,知截面和棱锥的底面平行,故④不正确;
对于⑤,如图2所示,在正方体中,四棱的四个侧面均为直角三角形,故⑤正确.
图1 图2
故答案为:⑤.
下列关于棱柱的说法:
①所有的面都是平行四边形;
②每一个面都不会是三角形;
③两底面平行,并且各侧棱也平行;
④棱柱的侧棱总与底面垂直.
其中说法正确的序号是_______.
【答案】③
【解析】
【分析】
根据棱柱的定义,逐项判断,即可求得答案.
【详解】
对于①,棱柱的底面不一定是平行四边形,如三棱柱、五棱柱等,故①错误;
对于②,棱柱的底面可以是三角形,故②错误;
对于③,由棱柱的特征性质可知:两底面平行,并且各侧棱也平行,故③正确;
对于④,棱柱的侧棱可能与底面垂直,也可能不与底面垂直,故④错误.
说法正确的序号是③.
故答案为:③.
题型三 旋转体的结构特征
例 3 下列命题中不正确的是( )
A.用平行于圆锥底面的平面截圆锥,截面与底面之间的部分是圆台
B.以直角梯形的一腰为轴,另一腰旋转形成的面是圆台的侧面
C.圆柱、圆锥、圆台的底面相似
D.圆台的母线延长后交于一点
【答案】B
【分析】
根据旋转体的结构特征进行判断.
【详解】
由圆柱、圆锥、圆台的概念及结构特征知均正确.
以直角梯形的直角腰为轴,另一腰旋转形成的面是圆台的侧面,以直角梯形的非直角腰为轴,另一腰旋转形成的面不是圆台的侧面.
故选B.
下列说法正确的是( )
A.以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥
B.以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台
C.圆柱、圆锥、圆台的底面都是圆面
D.一个平面截圆锥,得到一个圆锥和一个圆台
【答案】C
【分析】
根据旋转体的定义判断.
【详解】
以直角三角形的直角边所在直线为轴旋转一周所得的旋转体是圆锥,以斜边为轴旋转一周所得的旋转体是是两个同底圆锥的组合体,A错;
以直角梯形的直角腰所在直线为轴旋转一周所得的旋转体才是圆台,B错;
圆柱、圆锥、圆台的底面都是圆面,正确;
平行于圆锥底面平面截圆锥,得到一个圆锥和一个圆台,如果截面不平行于底面,则截得的不是圆锥和圆台,D错.
故选:C.
题型四 截面
例 4 用一个平面去截一个几何体,得到的截面是三角形,这个几何体可能是( )
A.圆柱 B.圆台 C.球体 D.棱台
【答案】D
【分析】
根据截面是三角形选出正确选项.
【详解】
圆柱、圆台、球体的截面不可能是三角形,棱台的截面可能是三角形.
故选:D
若用一个平面截一个几何体,能得到截面是等腰梯形,则这个几何体可能是( )
A.圆柱 B.圆锥 C.球 D.圆台
【答案】D
【分析】
根据圆台结构特征,可得结论.
【详解】
由台体的概念,可知D正确.
故选:D.
题型五 几何体的分类
例 5 设集合{正四棱柱},{长方体},{直四棱柱},{正方体},则这些集合间的关系是( )
A. B. C. D.
【答案】D
【分析】
先明确各个集合中几何体的主要特征,再判断集合关系.
【详解】
易知四种棱柱中正方体最特殊,直四棱柱最一般,而正四棱柱是底面为正方形的长方体,由此可知四个集合的关系为.
故选:D.
将下列各类几何体之间的关系用venn图表示出来:
多面体,长方体,棱柱,棱锥,棱台,直棱柱,四面体,平行六面体.
【答案】详见解析
【分析】
根据几何体的相关概念进行区分,多面体包含:棱柱,棱锥,棱台等,棱柱包含直棱柱和斜棱柱等.
【详解】
如图所示.
提升
1、下列几何体中旋转体__________个,台体(棱台和圆台)__________个.
【答案】
【分析】
根据几何体的结构特征判断可得出结论.
【详解】
由图可知,(6)(7)(8)为旋转体,(5)(7)为台体.
故答案为:;.
2、有下列三个说法:①两个互相平行的面是正方形,其余各面都是四边形的几何体一定是棱台;②有两个面平行且相似,其余各面都是梯形的多面体是棱台;③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.其中正确的有( )
A.0 B.1 C.2个 D.3个
【答案】A
【分析】
利用模型和反例进行判断.
【详解】
当两个互相平行的正方形全等时,不是棱台,故①中说法错误;②③可用反例去检验,如图(1)(2)所示,故②③中说法错误.
故选:A.
3、给出下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台的上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的;⑤圆台所有母线的延长线交于一点其中正确的命题是( )
A.①②④ B.②③④ C.①③⑤ D.②④⑤
【答案】D
【分析】
圆柱母线所在的直线互相平行且与旋转轴平行,判断①错误,④正确;由圆锥母线的定义知②正确;根据圆台定义,判断③错误,⑤正确.
【详解】
由于圆柱母线所在的直线互相平行且与旋转轴平行,
而在圆柱的上、下底面的圆周上各取一点,
这两点的连线与旋转轴不一定平行,故①错误,④正确;
由圆锥母线的定义知②正确;
在圆台的上、下底面的圆周上各取一点,这两点的连线不一定是母线,
且圆台所有母线的延长线交于一点,故③错误,⑤正确.
故选:D.
4、如图所示的平面中阴影部分绕旋转轴(虚线)旋转一周,形成的几何体为( )
A.一个球 B.一个球挖去一个圆柱
C.一个圆柱 D.一个球挖去一个长方体
【答案】B
【分析】
根据旋转体的定义,即可得出结论.
【详解】
由题意知形成的几何体为一个球挖去一个圆柱.
故选:B.
5、下列命题中正确的个数是( )
①由五个面围成的多面体只能是三棱柱;
②由若干个平面多边形所围成的几何体是多面体;
③仅有一组对面平行的五面体是棱台;
④有一面是多边形,其余各面是三角形的几何体是棱锥.
A.0 B.1 C.2 D.3
【答案】B
【分析】
举反例说明①③不正确;②是多面体的定义,正确;由棱锥的结构特征说明④错误.
【详解】
解:①中,由五个面围成的多面体可以是四棱锥,故①不正确;
②中,根据几何体的性质和结构特征可知,多面体是由若干个平面多边形所围成的几何体,故②正确;
③中,仅有一组对面平行的五面体,可以是三棱柱,故③不正确;
④中,有一个面是多边形,其余各面是三角形的几何体不一定是棱锥,
如图中的几何体,满足条件,但并不是棱锥,故④不正确.
故选:B.
6、下列说法正确的是( )
A.侧棱垂直于底面的棱柱一定是直棱柱
B.棱柱中两个互相平行的平面一定是棱柱的底面
C.棱柱中各条棱长都相等
D.棱柱的侧面是平行四边形,但它的底面一定不是平行四边形
【答案】A
【分析】
根据棱柱的定义和结构特征直接判断.
【详解】
A显然正确;
棱柱中两个互相平行的平面不一定是棱柱的底面,
例如正六棱柱的相对侧面,故B错误;
棱柱的每条侧棱长相等,而不是各条棱长都相等,故C错误;
棱柱的底面可以是平行四边形,如长方体,故D错误.
故选:A.
7、下面关于空间几何体的定义或结构特征叙述错误的是( )
A.空间中把一个平行四边形按某一方向平移所形成的几何体是四棱柱
B.有两个侧面都是矩形的三棱柱,它的侧棱垂直于底面
C.以直角三角形一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体是圆锥
D.底面是正多边形的棱锥的顶点在底面的射影一定是底面正多边形的中心
【答案】D
【分析】
根据四棱柱的定义可知A正确;直线与平面的判定定理可知B正确;根据圆锥的定义可知C正确;根据正棱锥的定义可知D错误.
【详解】
对于A,由四棱柱的定义:空间中把一个平行四边形按某一方向平移所形成的几何体是四棱柱,故A正确;
对于B,根据直线与平面的判定定理,得到这两个侧面的交线垂直于底面,是真命题,故B正确;
对于C,由圆锥的定义:以直角三角形一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体是圆锥,故C正确;
对于D,底面是正多边形的棱锥的顶点在底面的射影不一定是底面正多边形的中心,故D错误.
故选:D.
8、(多选)下列说法正确的是( )
A.以直角三角形的一条边所在直线为轴,其余两边旋转形成的曲面围成的几何体是圆锥
B.以等腰三角形底边上的中线所在直线为轴,将三角形旋转形成的曲面围成的几何体是圆锥
C.经过圆锥任意两条母线的截面是等腰三角形
D.圆锥侧面的母线长有可能大于圆锥底面圆的直径
【答案】BCD
【分析】
根据圆锥的概念及性质,各选项逐一判断即可得到答案.
【详解】
A不正确,直角三角形绕斜边所在直线旋转得到的旋转体不是圆锥;
B正确,以等腰三角形底边上的中线所在直线为轴,将三角形旋转形成的曲面围成的几何体是圆锥;
C正确,因为圆锥的母线长都相等,所以经过圆锥任意两条母线的截面是等腰三角形;
D正确,如图所示,圆锥侧面的母线长l有可能大于圆锥底面圆半径r的2倍(即直径).
故选:BCD.
9、(多选)下列说法错误的是( )
A.有一个面是多边形,其余各面都是三角形,由这些面围成的多面体是棱锥
B.有两个面平行且相似,其余各面都是梯形的多面体是棱台
C.如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥可能为六棱锥
D.如果一个棱柱的所有面都是长方形,那么这个棱柱是长方体
【答案】ABC
【分析】
选项不符合棱锥,棱台定义,所以错误;选项,会得出棱锥的各个侧面的共顶点的角之和是,构成平面图形,所以错误;选项,可推出侧棱与底面垂直,所以正确.
【详解】
选项A,有一个面是多边形,其余各面都是有一个公共顶点的三角形,
由这些面所围成的多面体叫做棱锥,即其余各面的三角形必须有公共的顶点,
故A错误;
选项B,棱台是由棱锥被平行于棱锥底面的平面所截而得的,
而有两个面平行且相似,其余各面都是梯形的多面体有可能不是棱台,
因为它的侧棱延长后不一定交于一点,故B错误;
选项C,当棱锥的各个侧面的共顶点的角之和是时,
各侧面构成平面图形,故这个棱锥不可能为六棱锥,故C错误;
选项D,若每个侧面都是长方形则说明侧棱与底面垂直,
又底面也是长方形,符合长方体的定义,故D正确.
故选:ABC.
10、如图所示的组合体,其结构特征是( )
A.左边是三棱台,右边是圆柱 B.左边是三棱柱,右边是圆柱
C.左边是三棱台,右边是长方体 D.左边是三棱柱,右边是长方体
【答案】D
【分析】
由已知图形,结合棱柱定义,即可得出结论.
【详解】
根据三棱柱和长方体的结构特征,可知此组合体左边是三棱柱,右边是长方体.
故选:D.
11、下列说法正确的有(______)个.
①有一个面是多边形,其余各面都是三角形的几何体是棱锥;
②正棱锥的侧面是等边三角形;
③底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
【答案】0
【分析】
根据棱锥的结构特征逐一判断:①根据棱锥的定义,“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”,故此说法是错误的;②正棱锥的侧面都是等腰三角形,不一定是等边三角形,故错误;③由已知条件知,此三棱锥的三个侧面未必全等,所以不一定是正三棱锥,故错误.
【详解】
①错误,根据棱锥的定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形而“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”,故此说法是错误的;
②错误,正棱锥的侧面都是等腰三角形,不一定是等边三角形,故错误;
③错误,由已知条件知,此三棱锥的三个侧面未必全等,所以不一定是正三棱锥.
如图所示的三棱锥中有,
满足底面为等边三角形,
三个侧面,,都是等腰三角形,
但长度不一定,三个侧面不一定全等,故错误.
故答案为:0.
12、(1)一个几何体由7个面围成,其中两个面是互相平行且全等的五边形,其他各面都是全等的矩形,则这个几何体是______.
(2)一个多面体最少有个_____面,此时这个多面体是______.
【答案】五棱柱 4 三棱锥或四面体
【分析】
根据空间几何体的主要特征进行求解.
【详解】
(1)两个面是互相平行且全等的五边形,其他各面都是全等的矩形,符合五棱柱的结构特征,所以是五棱柱;
(2)一个多面体最少有个4个面,少于4个面无法构成封闭的空间图形,由4个面组成的几何体是四面体或者三棱锥.
13、给出下列说法:(1)圆柱的底面是圆面;(2)经过圆柱任意两条母线的截面是一个矩形面;(3)圆台的任意两条母线的延长线可能相交,也可能不相交;(4)夹在圆柱的两个截面间的几何体还是一个旋转体.其中说法正确的是___________.(填序号)
【答案】(1)(2)
【分析】
根据常见几何体的特征逐个判定即可.
【详解】
(1)正确圆柱的底面是圆面;
(2)正确,如图所示,经过圆柱任意两条母线的截面是一个矩形面;
(3)不正确,圆台的任意两条母线延长后交于一点;
(4)不正确,夹在圆柱的两个平行于底面的截面间的几何体才是旋转体.
故答案为:(1)(2)
14、设有以下四个命题:
①底面是平行四边形的四棱柱是平行六面体;
②底面是矩形的平行六面体是长方体;
③直四棱柱是直平行六面体;
④棱台的相对侧棱延长后必交于一点.
其中正确命题的序号是______.
【答案】①④
【分析】
根据空间几何体的结构特征,依次判断各选项即可.
【详解】
命题①,符合平行六面体的定义,故命题①正确;
命题②,底面是矩形的平行六面体的侧棱可能与底面不垂直,故命题②错误;
命题③,因直四棱柱的底面不一定是平行四边形,故命题③错误;
命题④,由棱台的定义知,棱台的相对侧棱延长后必交于一点,故命题④正确.
综上可知,正确的为①④
故答案为: ①④
知识梳理
1、空间几何体
(1)空间中的物体都占据着空间的一部分,若只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.
(2)多面体
由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点.
2、棱柱、棱锥、棱台的概念
多面体 定义 图形及表示 相关概念
棱柱 有两个互相平行,其余各面都是平行四边形,并且每相邻两个四边形的公共边都相互平行,由这些边所围成的多面体叫做棱柱 如图可记作:棱柱AC′或
ABCD A′B′C′D′ 底面(底):两个相互平行的面 侧面:其余各面 侧棱:相邻侧面的公共边 顶点:侧面与底面的公共顶点
棱锥 有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫棱锥 如图可记作:棱锥SABCD 底面(底):多边形面. 侧面:有公共顶点的各个三角形 侧棱:相邻侧面的公共边 顶点:各侧面的公共顶点.
棱台 用一个平行于底面的平面去截棱锥,底面与截面之间的部分叫做棱台 如图可记作:棱台ABCDA′B′C′D′ 上底面:原棱锥的截面 下底面:原棱锥的底面 侧面:其余各面.侧棱:相邻侧面的公共边.顶点:侧面与上(下)底面的公共顶点
3、棱柱、棱锥、棱台的分类
(1)棱柱的分类
①按底面多边形的边数分类.
(
n
变形
)
②按侧棱与底面是否垂直分类.
(2)棱锥的分类(棱台分类)
①按底面多边形的边数分类.
三棱锥、四棱锥、五棱锥等.
②按底面多边形是否为正多边形分类.
正棱锥和一般棱锥.
4、旋转体
由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体,这条定直线叫做旋转体的轴.
5、圆柱、圆锥、圆台的概念
旋转体 结构特征 图示 表示法
圆柱 以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱.旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;无论旋转到什么位置,不垂直于轴边都叫做圆柱侧面的母线。圆柱和棱柱统称为柱体 圆柱用表示它的轴的字母表示,左图中圆柱表示为圆柱O′O
圆锥 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥.棱锥与圆锥统称为椎体 圆锥用表示它的轴的字母表示,左图中圆锥表示为 圆 锥SO
圆台 用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.与圆柱和圆锥一样,圆台也有轴、底面、侧面、母线.棱台与圆台统称为台体 圆台用表示它的轴的字母表示,左图中圆台表示为圆台O′O
6、球的概念
旋转体 结构特征 图示 表示法
球 以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球;半圆的圆心叫做球的球心;半圆的半径叫做球的半径;半圆的直径叫做球的直径 球常用表示球心的字母O表示,左图中的球表示为球O
7、简单组合体的结构特征.
(1)由简单几何体组合而成的几何体叫做简单组合体.
(2)简单组合体的两种基本形式:
简单组合体
知识典例
题型一 常见几何体的特征
例 1 观察图中的物体,说出它们的主要结构特征.
【答案】详见解析
【分析】
根据实物图抽象出几何图形,结合几何图形的特征进行识别.
【详解】
(1)圆台,它可看作用平行于圆锥底面的平面截圆锥,截面与底面之间的部分;
(2)圆柱,它可看作矩形绕其一边旋转一周,其余三边形成的面围成的几何体;
(3)球,它可看作半圆绕直径所在直线旋转一周,半圆形成的曲面围成的几何体;
(4)圆锥,它可看作由一个直角三角形绕其一条直角边所在直线旋转一周,另一条直角边和斜边形成的面围成的几何体.
巩固练习
说出图中物体的主要结构特征.
【答案】详见解析
【分析】
根据实物图抽象出几何图形,结合几何图形描述结构特征.
【详解】
(1)一个圆柱与一个圆锥的组合体,上部分为圆锥,下部分为圆柱;
(2)一个六棱柱里面挖去了一个圆柱.
题型二 棱柱的定义及几何特征
例 2 下列说法正确的是______(填序号).
①有两个面互相平行,其余各面都是四边形的几何体是棱柱;
②有两个面互相平行,其余各面都是平行四边形的几何体是棱柱;
③有一个面是多边形,其余各面都是三角形的几何体是棱锥;
④用一个平面去截棱锥,棱锥底面和截面之间那部分的几何体是棱台;
⑤存在一个四棱锥,其四个侧面都是直角三角形.
【答案】⑤
【分析】
根据棱柱、棱锥、棱台的定义判断①②③④,再举一例说明⑤正确.
【详解】
对于①,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,故①不正确;
对于②,如图1中的几何体,满足有两个面互相平行,其余各面都是平行四边形,但其不是棱柱,故②不正确;
对于③,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥,故③不正确;
对于④,由棱台的定义,知截面和棱锥的底面平行,故④不正确;
对于⑤,如图2所示,在正方体中,四棱的四个侧面均为直角三角形,故⑤正确.
图1 图2
故答案为:⑤.
下列关于棱柱的说法:
①所有的面都是平行四边形;
②每一个面都不会是三角形;
③两底面平行,并且各侧棱也平行;
④棱柱的侧棱总与底面垂直.
其中说法正确的序号是_______.
【答案】③
【解析】
【分析】
根据棱柱的定义,逐项判断,即可求得答案.
【详解】
对于①,棱柱的底面不一定是平行四边形,如三棱柱、五棱柱等,故①错误;
对于②,棱柱的底面可以是三角形,故②错误;
对于③,由棱柱的特征性质可知:两底面平行,并且各侧棱也平行,故③正确;
对于④,棱柱的侧棱可能与底面垂直,也可能不与底面垂直,故④错误.
说法正确的序号是③.
故答案为:③.
题型三 旋转体的结构特征
例 3 下列命题中不正确的是( )
A.用平行于圆锥底面的平面截圆锥,截面与底面之间的部分是圆台
B.以直角梯形的一腰为轴,另一腰旋转形成的面是圆台的侧面
C.圆柱、圆锥、圆台的底面相似
D.圆台的母线延长后交于一点
【答案】B
【分析】
根据旋转体的结构特征进行判断.
【详解】
由圆柱、圆锥、圆台的概念及结构特征知均正确.
以直角梯形的直角腰为轴,另一腰旋转形成的面是圆台的侧面,以直角梯形的非直角腰为轴,另一腰旋转形成的面不是圆台的侧面.
故选B.
下列说法正确的是( )
A.以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥
B.以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台
C.圆柱、圆锥、圆台的底面都是圆面
D.一个平面截圆锥,得到一个圆锥和一个圆台
【答案】C
【分析】
根据旋转体的定义判断.
【详解】
以直角三角形的直角边所在直线为轴旋转一周所得的旋转体是圆锥,以斜边为轴旋转一周所得的旋转体是是两个同底圆锥的组合体,A错;
以直角梯形的直角腰所在直线为轴旋转一周所得的旋转体才是圆台,B错;
圆柱、圆锥、圆台的底面都是圆面,正确;
平行于圆锥底面平面截圆锥,得到一个圆锥和一个圆台,如果截面不平行于底面,则截得的不是圆锥和圆台,D错.
故选:C.
题型四 截面
例 4 用一个平面去截一个几何体,得到的截面是三角形,这个几何体可能是( )
A.圆柱 B.圆台 C.球体 D.棱台
【答案】D
【分析】
根据截面是三角形选出正确选项.
【详解】
圆柱、圆台、球体的截面不可能是三角形,棱台的截面可能是三角形.
故选:D
若用一个平面截一个几何体,能得到截面是等腰梯形,则这个几何体可能是( )
A.圆柱 B.圆锥 C.球 D.圆台
【答案】D
【分析】
根据圆台结构特征,可得结论.
【详解】
由台体的概念,可知D正确.
故选:D.
题型五 几何体的分类
例 5 设集合{正四棱柱},{长方体},{直四棱柱},{正方体},则这些集合间的关系是( )
A. B. C. D.
【答案】D
【分析】
先明确各个集合中几何体的主要特征,再判断集合关系.
【详解】
易知四种棱柱中正方体最特殊,直四棱柱最一般,而正四棱柱是底面为正方形的长方体,由此可知四个集合的关系为.
故选:D.
将下列各类几何体之间的关系用venn图表示出来:
多面体,长方体,棱柱,棱锥,棱台,直棱柱,四面体,平行六面体.
【答案】详见解析
【分析】
根据几何体的相关概念进行区分,多面体包含:棱柱,棱锥,棱台等,棱柱包含直棱柱和斜棱柱等.
【详解】
如图所示.
提升
1、下列几何体中旋转体__________个,台体(棱台和圆台)__________个.
【答案】
【分析】
根据几何体的结构特征判断可得出结论.
【详解】
由图可知,(6)(7)(8)为旋转体,(5)(7)为台体.
故答案为:;.
2、有下列三个说法:①两个互相平行的面是正方形,其余各面都是四边形的几何体一定是棱台;②有两个面平行且相似,其余各面都是梯形的多面体是棱台;③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.其中正确的有( )
A.0 B.1 C.2个 D.3个
【答案】A
【分析】
利用模型和反例进行判断.
【详解】
当两个互相平行的正方形全等时,不是棱台,故①中说法错误;②③可用反例去检验,如图(1)(2)所示,故②③中说法错误.
故选:A.
3、给出下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台的上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的;⑤圆台所有母线的延长线交于一点其中正确的命题是( )
A.①②④ B.②③④ C.①③⑤ D.②④⑤
【答案】D
【分析】
圆柱母线所在的直线互相平行且与旋转轴平行,判断①错误,④正确;由圆锥母线的定义知②正确;根据圆台定义,判断③错误,⑤正确.
【详解】
由于圆柱母线所在的直线互相平行且与旋转轴平行,
而在圆柱的上、下底面的圆周上各取一点,
这两点的连线与旋转轴不一定平行,故①错误,④正确;
由圆锥母线的定义知②正确;
在圆台的上、下底面的圆周上各取一点,这两点的连线不一定是母线,
且圆台所有母线的延长线交于一点,故③错误,⑤正确.
故选:D.
4、如图所示的平面中阴影部分绕旋转轴(虚线)旋转一周,形成的几何体为( )
A.一个球 B.一个球挖去一个圆柱
C.一个圆柱 D.一个球挖去一个长方体
【答案】B
【分析】
根据旋转体的定义,即可得出结论.
【详解】
由题意知形成的几何体为一个球挖去一个圆柱.
故选:B.
5、下列命题中正确的个数是( )
①由五个面围成的多面体只能是三棱柱;
②由若干个平面多边形所围成的几何体是多面体;
③仅有一组对面平行的五面体是棱台;
④有一面是多边形,其余各面是三角形的几何体是棱锥.
A.0 B.1 C.2 D.3
【答案】B
【分析】
举反例说明①③不正确;②是多面体的定义,正确;由棱锥的结构特征说明④错误.
【详解】
解:①中,由五个面围成的多面体可以是四棱锥,故①不正确;
②中,根据几何体的性质和结构特征可知,多面体是由若干个平面多边形所围成的几何体,故②正确;
③中,仅有一组对面平行的五面体,可以是三棱柱,故③不正确;
④中,有一个面是多边形,其余各面是三角形的几何体不一定是棱锥,
如图中的几何体,满足条件,但并不是棱锥,故④不正确.
故选:B.
6、下列说法正确的是( )
A.侧棱垂直于底面的棱柱一定是直棱柱
B.棱柱中两个互相平行的平面一定是棱柱的底面
C.棱柱中各条棱长都相等
D.棱柱的侧面是平行四边形,但它的底面一定不是平行四边形
【答案】A
【分析】
根据棱柱的定义和结构特征直接判断.
【详解】
A显然正确;
棱柱中两个互相平行的平面不一定是棱柱的底面,
例如正六棱柱的相对侧面,故B错误;
棱柱的每条侧棱长相等,而不是各条棱长都相等,故C错误;
棱柱的底面可以是平行四边形,如长方体,故D错误.
故选:A.
7、下面关于空间几何体的定义或结构特征叙述错误的是( )
A.空间中把一个平行四边形按某一方向平移所形成的几何体是四棱柱
B.有两个侧面都是矩形的三棱柱,它的侧棱垂直于底面
C.以直角三角形一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体是圆锥
D.底面是正多边形的棱锥的顶点在底面的射影一定是底面正多边形的中心
【答案】D
【分析】
根据四棱柱的定义可知A正确;直线与平面的判定定理可知B正确;根据圆锥的定义可知C正确;根据正棱锥的定义可知D错误.
【详解】
对于A,由四棱柱的定义:空间中把一个平行四边形按某一方向平移所形成的几何体是四棱柱,故A正确;
对于B,根据直线与平面的判定定理,得到这两个侧面的交线垂直于底面,是真命题,故B正确;
对于C,由圆锥的定义:以直角三角形一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体是圆锥,故C正确;
对于D,底面是正多边形的棱锥的顶点在底面的射影不一定是底面正多边形的中心,故D错误.
故选:D.
8、(多选)下列说法正确的是( )
A.以直角三角形的一条边所在直线为轴,其余两边旋转形成的曲面围成的几何体是圆锥
B.以等腰三角形底边上的中线所在直线为轴,将三角形旋转形成的曲面围成的几何体是圆锥
C.经过圆锥任意两条母线的截面是等腰三角形
D.圆锥侧面的母线长有可能大于圆锥底面圆的直径
【答案】BCD
【分析】
根据圆锥的概念及性质,各选项逐一判断即可得到答案.
【详解】
A不正确,直角三角形绕斜边所在直线旋转得到的旋转体不是圆锥;
B正确,以等腰三角形底边上的中线所在直线为轴,将三角形旋转形成的曲面围成的几何体是圆锥;
C正确,因为圆锥的母线长都相等,所以经过圆锥任意两条母线的截面是等腰三角形;
D正确,如图所示,圆锥侧面的母线长l有可能大于圆锥底面圆半径r的2倍(即直径).
故选:BCD.
9、(多选)下列说法错误的是( )
A.有一个面是多边形,其余各面都是三角形,由这些面围成的多面体是棱锥
B.有两个面平行且相似,其余各面都是梯形的多面体是棱台
C.如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥可能为六棱锥
D.如果一个棱柱的所有面都是长方形,那么这个棱柱是长方体
【答案】ABC
【分析】
选项不符合棱锥,棱台定义,所以错误;选项,会得出棱锥的各个侧面的共顶点的角之和是,构成平面图形,所以错误;选项,可推出侧棱与底面垂直,所以正确.
【详解】
选项A,有一个面是多边形,其余各面都是有一个公共顶点的三角形,
由这些面所围成的多面体叫做棱锥,即其余各面的三角形必须有公共的顶点,
故A错误;
选项B,棱台是由棱锥被平行于棱锥底面的平面所截而得的,
而有两个面平行且相似,其余各面都是梯形的多面体有可能不是棱台,
因为它的侧棱延长后不一定交于一点,故B错误;
选项C,当棱锥的各个侧面的共顶点的角之和是时,
各侧面构成平面图形,故这个棱锥不可能为六棱锥,故C错误;
选项D,若每个侧面都是长方形则说明侧棱与底面垂直,
又底面也是长方形,符合长方体的定义,故D正确.
故选:ABC.
10、如图所示的组合体,其结构特征是( )
A.左边是三棱台,右边是圆柱 B.左边是三棱柱,右边是圆柱
C.左边是三棱台,右边是长方体 D.左边是三棱柱,右边是长方体
【答案】D
【分析】
由已知图形,结合棱柱定义,即可得出结论.
【详解】
根据三棱柱和长方体的结构特征,可知此组合体左边是三棱柱,右边是长方体.
故选:D.
11、下列说法正确的有(______)个.
①有一个面是多边形,其余各面都是三角形的几何体是棱锥;
②正棱锥的侧面是等边三角形;
③底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
【答案】0
【分析】
根据棱锥的结构特征逐一判断:①根据棱锥的定义,“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”,故此说法是错误的;②正棱锥的侧面都是等腰三角形,不一定是等边三角形,故错误;③由已知条件知,此三棱锥的三个侧面未必全等,所以不一定是正三棱锥,故错误.
【详解】
①错误,根据棱锥的定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形而“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”,故此说法是错误的;
②错误,正棱锥的侧面都是等腰三角形,不一定是等边三角形,故错误;
③错误,由已知条件知,此三棱锥的三个侧面未必全等,所以不一定是正三棱锥.
如图所示的三棱锥中有,
满足底面为等边三角形,
三个侧面,,都是等腰三角形,
但长度不一定,三个侧面不一定全等,故错误.
故答案为:0.
12、(1)一个几何体由7个面围成,其中两个面是互相平行且全等的五边形,其他各面都是全等的矩形,则这个几何体是______.
(2)一个多面体最少有个_____面,此时这个多面体是______.
【答案】五棱柱 4 三棱锥或四面体
【分析】
根据空间几何体的主要特征进行求解.
【详解】
(1)两个面是互相平行且全等的五边形,其他各面都是全等的矩形,符合五棱柱的结构特征,所以是五棱柱;
(2)一个多面体最少有个4个面,少于4个面无法构成封闭的空间图形,由4个面组成的几何体是四面体或者三棱锥.
13、给出下列说法:(1)圆柱的底面是圆面;(2)经过圆柱任意两条母线的截面是一个矩形面;(3)圆台的任意两条母线的延长线可能相交,也可能不相交;(4)夹在圆柱的两个截面间的几何体还是一个旋转体.其中说法正确的是___________.(填序号)
【答案】(1)(2)
【分析】
根据常见几何体的特征逐个判定即可.
【详解】
(1)正确圆柱的底面是圆面;
(2)正确,如图所示,经过圆柱任意两条母线的截面是一个矩形面;
(3)不正确,圆台的任意两条母线延长后交于一点;
(4)不正确,夹在圆柱的两个平行于底面的截面间的几何体才是旋转体.
故答案为:(1)(2)
14、设有以下四个命题:
①底面是平行四边形的四棱柱是平行六面体;
②底面是矩形的平行六面体是长方体;
③直四棱柱是直平行六面体;
④棱台的相对侧棱延长后必交于一点.
其中正确命题的序号是______.
【答案】①④
【分析】
根据空间几何体的结构特征,依次判断各选项即可.
【详解】
命题①,符合平行六面体的定义,故命题①正确;
命题②,底面是矩形的平行六面体的侧棱可能与底面不垂直,故命题②错误;
命题③,因直四棱柱的底面不一定是平行四边形,故命题③错误;
命题④,由棱台的定义知,棱台的相对侧棱延长后必交于一点,故命题④正确.
综上可知,正确的为①④
故答案为: ①④
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
