人教版数学九年级上册22.1.2二次函数y=ax2(a≠0)的图像和性质 课件(共26张PPT)
文档属性
| 名称 | 人教版数学九年级上册22.1.2二次函数y=ax2(a≠0)的图像和性质 课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 11:09:26 | ||
图片预览







文档简介
(共26张PPT)
义务教育人教版初中数学九年级上册
冬 藏
胜利三中:孙贵超
忆一忆
1.正比例函数y=kx(k≠0)的图像是一条经过
的一条 .
填空:
2.当 时,正比例函数y=kx(k≠0)的
图像经过原点和一、三象限。此时y随x的增大而
当 时,正比例函数y=kx(k≠0)的
图像经过原点和二、四象限。此时y随x的增大而
K的符号决定了正比例函数函数值随自
变量的变化情况
原点
直线
k>0
k<0
增大
减小
冬 藏
胜利三中:孙贵超
忆一忆
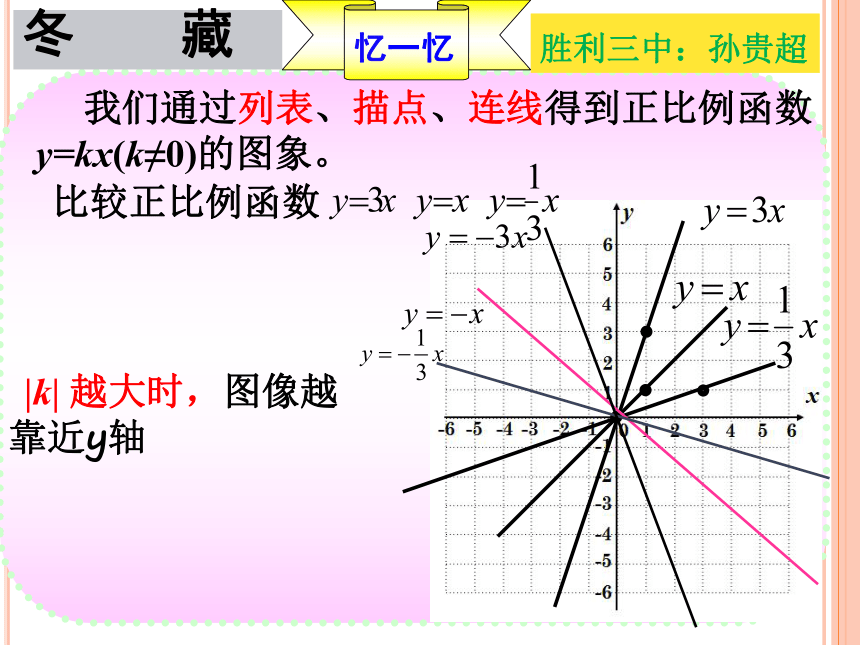
我们通过列表、描点、连线得到正比例函数
y=kx(k≠0)的图象。
比较正比例函数
|k| 越大时,图像越
靠近y轴
冬 藏
胜利三中:孙贵超
忆一忆
函数y=kx(k≠0)的图像与一次项系数k的关系
k的符号决定了正比例函数函数值随自
变量的变化情况
|k| 越大时,图像越靠近y轴
那么函数y=ax2(a≠0)的图像与系数a的
又有怎样的关系呢?
胜利三中:孙贵超
春 耕
画出二次函数 的图像。
试一试
胜利三中:孙贵超
春 耕
x
y=x2
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
函数图象画法
列表
描点
连线
0
0.25
1
2.25
4
0.25
1
2.25
4
描点法
胜利三中:孙贵超
春 耕
对称轴与抛物线的交点
叫做抛物线的顶点。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
二次函数y=ax2的图象形如
物体抛射时所经过的路线,
我们把它叫做抛物线。
函数y=ax2(k≠0)的图像的几个基本知识点
胜利三中:孙贵超
春 耕
探究一
函数y=ax2(k≠0)的图像与系数a的符号的关系
以函数y=x2,与函数y= - x2为例
y=-x2
出现了怎样的变化?
开口方向
函数值y随自变量的变化
情况呢?
对称轴左侧
对称轴右侧
*
胜利三中:孙贵超
春 耕
归纳整合
(0,0)
(0,0)
y轴
y轴
左 x↗y↘右x↗y ↗
向下
当x=0时,最小值为0
当x=0时,最大值为0
抛物线
顶点坐标
对称轴
开口方向
增减性
极值
向上
左 x↗y ↗右x↗y↘
y=x2
y=-x2
a的符号抛物线的开口方向
胜利三中:孙贵超
夏 耘
探究二
函数y=ax2(k≠0)的图像与系数|a|的关系
y=2x2
y=x2
y=0.5x2
y=0.25x2
y=-2x2
y=-x2
y=-0.5x2
y= -0.25x2
|a|的大小决定了抛物线开口的大小
胜利三中:孙贵超
夏 耘
归纳整合
(0,0)
(0,0)
y轴
y轴
左 x↗y↘右x↗y ↗
向下
当x=0时,最小值为0
当x=0时,最大值为0
抛物线
顶点坐标
对称轴
开口方向
增减性
极值
向上
左 x↗y ↗右x↗y↘
y=ax2 (a>0)
y= -ax2 (a>0)
开口大小
|a| ↗开口↘ |a| ↘ 开口↗
|a| ↗开口↘ |a| ↘ 开口↗
a决定了抛物线的形状!!
胜利三中:孙贵超
冬 藏
秋 收
练一练
1、根据左边已画好的函数图象填空:
(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,
在 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外)。
(0,0)
y轴
对称轴的右
对称轴的左
0
0
上
胜利三中:孙贵超
冬 藏
秋 收
练一练
(2)抛物线 在x轴的
方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,当x 0时y<0.
下
增大而增大
增大而减小
0
胜利三中:孙贵超
冬 藏
秋 收
练一练
2.说出下列抛物线的开口方向、对称轴和顶点
(1)y=3x2
(2)y= -3x2
(3)
(4)
胜利三中:孙贵超
冬 藏
秋 收
议一议
已知:P(a1,b1),Q(a2,b2)
是抛物线 上的两点.
2.若a1= -3,a2= -2;则
b1 b2(用不等号填空)
1.若a1=3,a2=2;则
b1 b2(用不等号填空)
3.若a1= -3,a2= 2;则
b1 b2(用不等号填空)
4.若a1>a2>0;则
b1 b2(用不等号填空)
5.若a1b1 b2(用不等号填空)
6.若a1+a2>0;a1 a2<0
且|a1| <|a2| 则b1 b2
(用不等号填空)
>
<
>
>
>
>
7.若|a1| <|a2| 则b1 b2
(用不等号填空)
<
胜利三中:孙贵超
冬 藏
秋 收
变式练习
已知:P(a1,b1),Q(a2,b2)
是抛物线 上的两点.
1.若a1>a2>0;则
b1 b2(用不等号填空)
2.若a1b1 b2(用不等号填空)
3.若a1+a2>0;a1 a2<0
且|a1| <|a2| 则b1 b2
(用不等号填空)
<
>
<
4.若|a1| >|a2| 则b1 b2
(用不等号填空)
<
胜利三中:孙贵超
冬 藏
归 仓
这节课上,我感受最深的是……
这节课上,我感到最困难的是……
这节课上,我学会了……
……
自己总结,小组内交流。
类比思想
数形结合思想
胜利三中:孙贵超
归 仓
归纳整合
(0,0)
(0,0)
y轴
y轴
左 x↗y↘右x↗y ↗
向下
当x=0时,最小值为0
当x=0时,最大值为0
抛物线
顶点坐标
对称轴
开口方向
增减性
极值
向上
左 x↗y ↗右x↗y↘
y=ax2 (a>0)
y= -ax2 (a>0)
开口大小
a决定了抛物线的形状!!
|a| ↗开口↘ |a| ↘ 开口↗
|a| ↗开口↘ |a| ↘ 开口↗
胜利三中:孙贵超
展 望
胜利三中:孙贵超
冬 藏
沉淀内化
智慧大课堂 23页、24页
义务教育人教版初中数学九年级上册
冬 藏
胜利三中:孙贵超
忆一忆
1.正比例函数y=kx(k≠0)的图像是一条经过
的一条 .
填空:
2.当 时,正比例函数y=kx(k≠0)的
图像经过原点和一、三象限。此时y随x的增大而
当 时,正比例函数y=kx(k≠0)的
图像经过原点和二、四象限。此时y随x的增大而
K的符号决定了正比例函数函数值随自
变量的变化情况
原点
直线
k>0
k<0
增大
减小
冬 藏
胜利三中:孙贵超
忆一忆
我们通过列表、描点、连线得到正比例函数
y=kx(k≠0)的图象。
比较正比例函数
|k| 越大时,图像越
靠近y轴
冬 藏
胜利三中:孙贵超
忆一忆
函数y=kx(k≠0)的图像与一次项系数k的关系
k的符号决定了正比例函数函数值随自
变量的变化情况
|k| 越大时,图像越靠近y轴
那么函数y=ax2(a≠0)的图像与系数a的
又有怎样的关系呢?
胜利三中:孙贵超
春 耕
画出二次函数 的图像。
试一试
胜利三中:孙贵超
春 耕
x
y=x2
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
函数图象画法
列表
描点
连线
0
0.25
1
2.25
4
0.25
1
2.25
4
描点法
胜利三中:孙贵超
春 耕
对称轴与抛物线的交点
叫做抛物线的顶点。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
二次函数y=ax2的图象形如
物体抛射时所经过的路线,
我们把它叫做抛物线。
函数y=ax2(k≠0)的图像的几个基本知识点
胜利三中:孙贵超
春 耕
探究一
函数y=ax2(k≠0)的图像与系数a的符号的关系
以函数y=x2,与函数y= - x2为例
y=-x2
出现了怎样的变化?
开口方向
函数值y随自变量的变化
情况呢?
对称轴左侧
对称轴右侧
*
胜利三中:孙贵超
春 耕
归纳整合
(0,0)
(0,0)
y轴
y轴
左 x↗y↘右x↗y ↗
向下
当x=0时,最小值为0
当x=0时,最大值为0
抛物线
顶点坐标
对称轴
开口方向
增减性
极值
向上
左 x↗y ↗右x↗y↘
y=x2
y=-x2
a的符号抛物线的开口方向
胜利三中:孙贵超
夏 耘
探究二
函数y=ax2(k≠0)的图像与系数|a|的关系
y=2x2
y=x2
y=0.5x2
y=0.25x2
y=-2x2
y=-x2
y=-0.5x2
y= -0.25x2
|a|的大小决定了抛物线开口的大小
胜利三中:孙贵超
夏 耘
归纳整合
(0,0)
(0,0)
y轴
y轴
左 x↗y↘右x↗y ↗
向下
当x=0时,最小值为0
当x=0时,最大值为0
抛物线
顶点坐标
对称轴
开口方向
增减性
极值
向上
左 x↗y ↗右x↗y↘
y=ax2 (a>0)
y= -ax2 (a>0)
开口大小
|a| ↗开口↘ |a| ↘ 开口↗
|a| ↗开口↘ |a| ↘ 开口↗
a决定了抛物线的形状!!
胜利三中:孙贵超
冬 藏
秋 收
练一练
1、根据左边已画好的函数图象填空:
(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,
在 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外)。
(0,0)
y轴
对称轴的右
对称轴的左
0
0
上
胜利三中:孙贵超
冬 藏
秋 收
练一练
(2)抛物线 在x轴的
方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,当x 0时y<0.
下
增大而增大
增大而减小
0
胜利三中:孙贵超
冬 藏
秋 收
练一练
2.说出下列抛物线的开口方向、对称轴和顶点
(1)y=3x2
(2)y= -3x2
(3)
(4)
胜利三中:孙贵超
冬 藏
秋 收
议一议
已知:P(a1,b1),Q(a2,b2)
是抛物线 上的两点.
2.若a1= -3,a2= -2;则
b1 b2(用不等号填空)
1.若a1=3,a2=2;则
b1 b2(用不等号填空)
3.若a1= -3,a2= 2;则
b1 b2(用不等号填空)
4.若a1>a2>0;则
b1 b2(用不等号填空)
5.若a1
6.若a1+a2>0;a1 a2<0
且|a1| <|a2| 则b1 b2
(用不等号填空)
>
<
>
>
>
>
7.若|a1| <|a2| 则b1 b2
(用不等号填空)
<
胜利三中:孙贵超
冬 藏
秋 收
变式练习
已知:P(a1,b1),Q(a2,b2)
是抛物线 上的两点.
1.若a1>a2>0;则
b1 b2(用不等号填空)
2.若a1
3.若a1+a2>0;a1 a2<0
且|a1| <|a2| 则b1 b2
(用不等号填空)
<
>
<
4.若|a1| >|a2| 则b1 b2
(用不等号填空)
<
胜利三中:孙贵超
冬 藏
归 仓
这节课上,我感受最深的是……
这节课上,我感到最困难的是……
这节课上,我学会了……
……
自己总结,小组内交流。
类比思想
数形结合思想
胜利三中:孙贵超
归 仓
归纳整合
(0,0)
(0,0)
y轴
y轴
左 x↗y↘右x↗y ↗
向下
当x=0时,最小值为0
当x=0时,最大值为0
抛物线
顶点坐标
对称轴
开口方向
增减性
极值
向上
左 x↗y ↗右x↗y↘
y=ax2 (a>0)
y= -ax2 (a>0)
开口大小
a决定了抛物线的形状!!
|a| ↗开口↘ |a| ↘ 开口↗
|a| ↗开口↘ |a| ↘ 开口↗
胜利三中:孙贵超
展 望
胜利三中:孙贵超
冬 藏
沉淀内化
智慧大课堂 23页、24页
同课章节目录
