4.2图形的全等 课件(共28张PPT)
文档属性
| 名称 | 4.2图形的全等 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 572.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 08:20:45 | ||
图片预览




文档简介
(共28张PPT)
北师大版七年级下册数学
第四章 三角形
4.2 图形的全等
这些是我们熟悉的图形,它们有什么特点?
情景引入
(7)
(6)
(3)
(1)
(2)
(4)
(5)
(8)
(9)
(10)
(11)
(12)
这些图形中有些是完全一样的,如果把它们叠在一起,它们就能重合. 你能从图中找出这样的图形吗?
一、全等图形
探究新知
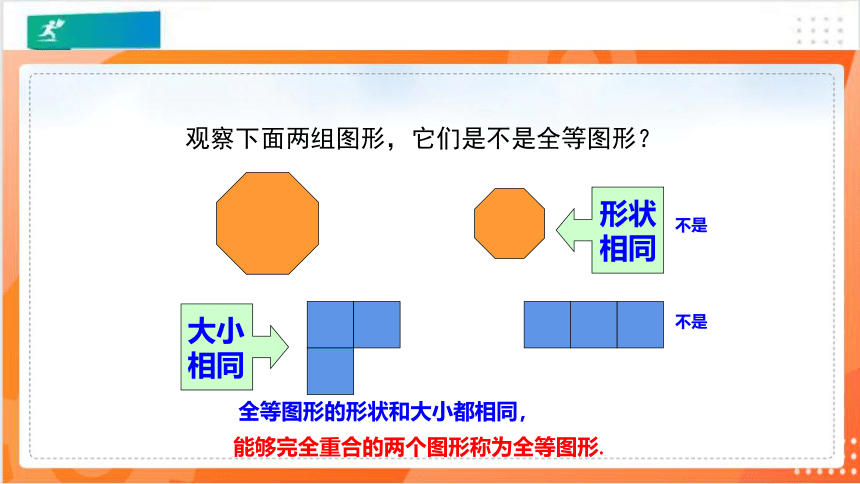
全等图形的形状和大小都相同,
大小
相同
观察下面两组图形,它们是不是全等图形?
形状
相同
能够完全重合的两个图形称为全等图形.
不是
不是
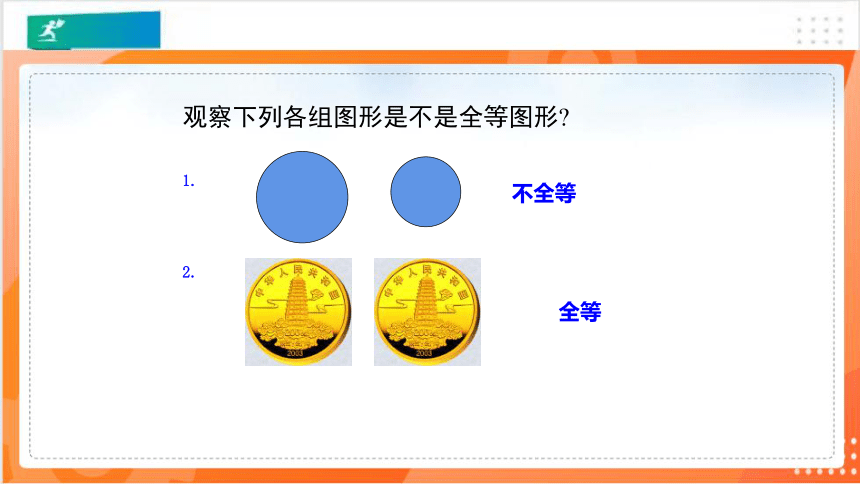
观察下列各组图形是不是全等图形
1.
2.
不全等
全等
(1)
(2)
(3)
(4)
(5)
(10)
(6)
(11)
(12)
(13)
(7)
(8)
(9)
(14)
(15)
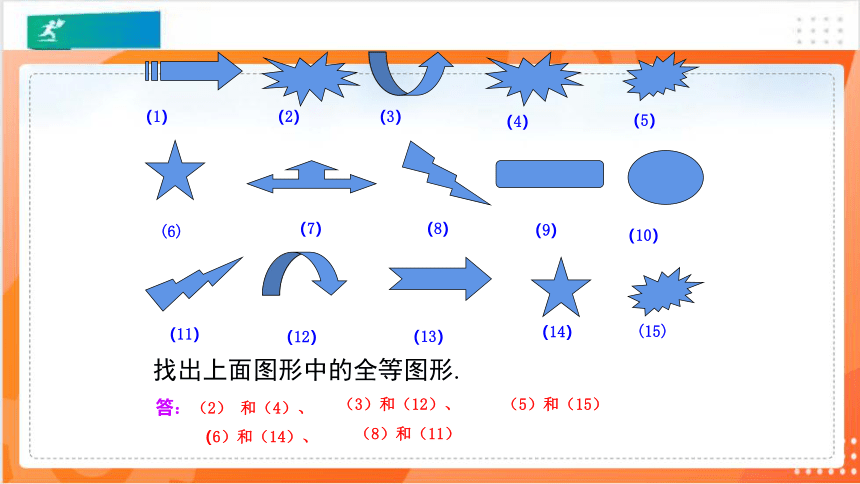
答:(2) 和(4)、
(5)和(15)
(3)和(12)、
(6)和(14)、
(8)和(11)
找出上面图形中的全等图形.
沿图形中的虚线,分别把下面图形划分为两个全等图形(至少找出两种方法),并与同伴交流.
【做一做】
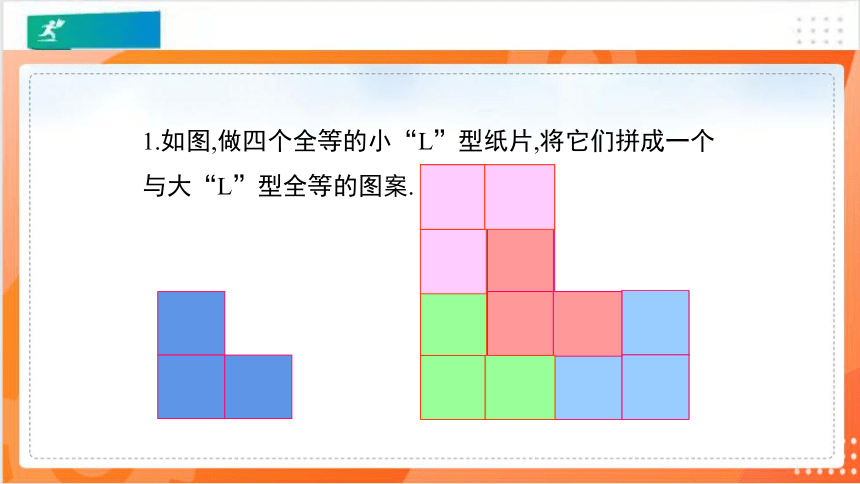
1.如图,做四个全等的小“L”型纸片,将它们拼成一个与大“L”型全等的图案.
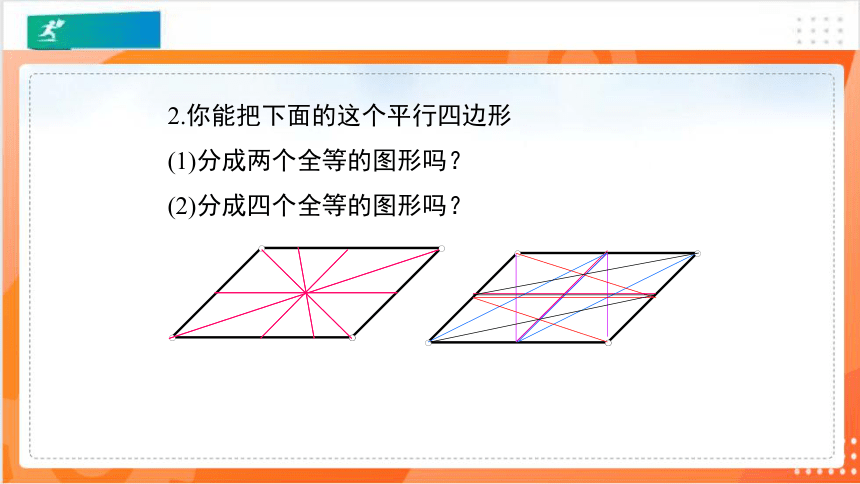
2.你能把下面的这个平行四边形
(1)分成两个全等的图形吗?
(2)分成四个全等的图形吗?
E
D
F
E
D
F
A
B
C
像上图一样,把△ABC叠到△DEF上,能够完全重合的两个三角形,叫作全等三角形.
把两个全等的三角形重叠到一起时,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.
你能指出上面两个全等三角形的对应顶点、对应边、对应角吗?
二、全等三角形的定义及性质
探究新知
△ABC≌△FDE
A
B
C
E
D
F
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
例:如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
典例精析
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,
∠AOD与∠AOE.
A
D
F
C
E
B
1
2
A
B
D
C
1
4
2
3
E
A
B
C
F
1
2
3
4
找一找下列全等图形的对应元素?
A
B
C
D
F
请你利用自制的一对全等三角形拼出有公共顶点或公共边或公共角的图形.试用全等符号表示它们,分析每个图形,找准对应边、对应角.
A
B
C
D
A
B
C
D
A
B
C
D
1.有公共边
寻找对应边、对应角有什么规律
探究归纳
1. 有公共边,则公共边为对应边;
2. 有公共角(对顶角),则公共角(对顶角)为对应角;
3.最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角;
4. 对应角的对边为对应边;对应边的对角为对应角.
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
2.有公共点
总结归纳
A
B
C
E
D
F
∵△ABC≌△DEF(已知),
∴AB=DE, AC=DF,BC=EF(全等三角形对
应边相等),
∠A=∠D, ∠B=∠E, ∠C=∠F(全等三角形对应角相等).
全等三角形的对应边相等;
全等三角形的对应角相等.
全等的性质
∵△ABC≌△FDE
∴A B=F D,A C=F E,B C=D E(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E(全等三角形对应角相等)
A
B
C
E
D
F
全等三角形的性质的几何语言
试一试:
如图,△ABC与△ADC全等,请用数学符号表示出
这两个三角形全等,并写出相等的边和角.
解:△ABC≌△ADC;
相等的边为:AB=AD,AC=AC,BC=DC;
相等的角为:∠BAC=∠DAC,∠B=∠D,∠ACB=∠ACD.
例1 如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
例2 如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
解:(1)对应边有EF和NM,FG和MH,EG和NH;
对应角有∠E和∠N, ∠F和∠M, ∠EGF和∠NHM.
(2)求线段NM及HG的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并证明.
解:∵ △EFG≌△NMH,
∴NM=EF=2.1cm,
EG=NH=3.3cm.
∴HG=EG –EH=3.3-1.1=2.2(cm).
解:结论:EF∥NM
证明: ∵ △EFG≌△NMH,
∴ ∠E=∠N. ∴ EF∥NM.
想一想:你还能得出
其他结论吗?
1.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是( )
A.5 B.4 C.3 D.2
【解析】选A.AB=BE+AE=4+1=5,因为△ABC≌△DEF,所以DE=AB=5.
D
E
A
B
F
C
课堂练习
【解析】因为△AEC≌△ABC,
所以∠E=∠B=30°,
∠ACE=∠ACB=85°,
∠EAC=∠BAC=180°- 30°-85°=65°.
2.如图:△ABC≌△AEC, ∠B=30°, ∠ACB=85°,
求出△AEC各内角的度数.
A
B
C
E
3.如图:△AOD≌△BOC,写出其中相等的角.
A
D
C
B
O
【解析】由全等三角形对应角相等可得:
∠A=∠B,
∠D=∠C,
∠DOA=∠COB.
4.如图,△ABC≌△DEF,∠B=25°,BC=6cm,AC=4cm ,
你能得出△DEF中哪些角的大小,哪些边的长度
A
B
C
D
E
F
因为△DEF≌△ABC,
所以∠E=∠B=25°,
EF=BC=6cm,
DF=AC=4cm.
【解析】
5.如图,一栅栏顶部是由全等的三角形组成的,其中AC=0.2m ,BC=2AC,求BD的长.
A
B
C
D
【解析】
根据题意得
BD=7BC=7×2AC=7×2×0.2
=2.8(m)
1.能够完全重合的两个图形称为全等图形.
2.全等图形的形状和大小都相同,与位置无关.
3.全等三角形的对应边相等,对应角相等.
通过本课时的学习,需要我们掌握:
课堂小结
https://www.21cnjy.com/help/help_extract.php
北师大版七年级下册数学
第四章 三角形
4.2 图形的全等
这些是我们熟悉的图形,它们有什么特点?
情景引入
(7)
(6)
(3)
(1)
(2)
(4)
(5)
(8)
(9)
(10)
(11)
(12)
这些图形中有些是完全一样的,如果把它们叠在一起,它们就能重合. 你能从图中找出这样的图形吗?
一、全等图形
探究新知
全等图形的形状和大小都相同,
大小
相同
观察下面两组图形,它们是不是全等图形?
形状
相同
能够完全重合的两个图形称为全等图形.
不是
不是
观察下列各组图形是不是全等图形
1.
2.
不全等
全等
(1)
(2)
(3)
(4)
(5)
(10)
(6)
(11)
(12)
(13)
(7)
(8)
(9)
(14)
(15)
答:(2) 和(4)、
(5)和(15)
(3)和(12)、
(6)和(14)、
(8)和(11)
找出上面图形中的全等图形.
沿图形中的虚线,分别把下面图形划分为两个全等图形(至少找出两种方法),并与同伴交流.
【做一做】
1.如图,做四个全等的小“L”型纸片,将它们拼成一个与大“L”型全等的图案.
2.你能把下面的这个平行四边形
(1)分成两个全等的图形吗?
(2)分成四个全等的图形吗?
E
D
F
E
D
F
A
B
C
像上图一样,把△ABC叠到△DEF上,能够完全重合的两个三角形,叫作全等三角形.
把两个全等的三角形重叠到一起时,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.
你能指出上面两个全等三角形的对应顶点、对应边、对应角吗?
二、全等三角形的定义及性质
探究新知
△ABC≌△FDE
A
B
C
E
D
F
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
例:如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
典例精析
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,
∠AOD与∠AOE.
A
D
F
C
E
B
1
2
A
B
D
C
1
4
2
3
E
A
B
C
F
1
2
3
4
找一找下列全等图形的对应元素?
A
B
C
D
F
请你利用自制的一对全等三角形拼出有公共顶点或公共边或公共角的图形.试用全等符号表示它们,分析每个图形,找准对应边、对应角.
A
B
C
D
A
B
C
D
A
B
C
D
1.有公共边
寻找对应边、对应角有什么规律
探究归纳
1. 有公共边,则公共边为对应边;
2. 有公共角(对顶角),则公共角(对顶角)为对应角;
3.最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角;
4. 对应角的对边为对应边;对应边的对角为对应角.
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
2.有公共点
总结归纳
A
B
C
E
D
F
∵△ABC≌△DEF(已知),
∴AB=DE, AC=DF,BC=EF(全等三角形对
应边相等),
∠A=∠D, ∠B=∠E, ∠C=∠F(全等三角形对应角相等).
全等三角形的对应边相等;
全等三角形的对应角相等.
全等的性质
∵△ABC≌△FDE
∴A B=F D,A C=F E,B C=D E(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E(全等三角形对应角相等)
A
B
C
E
D
F
全等三角形的性质的几何语言
试一试:
如图,△ABC与△ADC全等,请用数学符号表示出
这两个三角形全等,并写出相等的边和角.
解:△ABC≌△ADC;
相等的边为:AB=AD,AC=AC,BC=DC;
相等的角为:∠BAC=∠DAC,∠B=∠D,∠ACB=∠ACD.
例1 如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
例2 如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
解:(1)对应边有EF和NM,FG和MH,EG和NH;
对应角有∠E和∠N, ∠F和∠M, ∠EGF和∠NHM.
(2)求线段NM及HG的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并证明.
解:∵ △EFG≌△NMH,
∴NM=EF=2.1cm,
EG=NH=3.3cm.
∴HG=EG –EH=3.3-1.1=2.2(cm).
解:结论:EF∥NM
证明: ∵ △EFG≌△NMH,
∴ ∠E=∠N. ∴ EF∥NM.
想一想:你还能得出
其他结论吗?
1.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是( )
A.5 B.4 C.3 D.2
【解析】选A.AB=BE+AE=4+1=5,因为△ABC≌△DEF,所以DE=AB=5.
D
E
A
B
F
C
课堂练习
【解析】因为△AEC≌△ABC,
所以∠E=∠B=30°,
∠ACE=∠ACB=85°,
∠EAC=∠BAC=180°- 30°-85°=65°.
2.如图:△ABC≌△AEC, ∠B=30°, ∠ACB=85°,
求出△AEC各内角的度数.
A
B
C
E
3.如图:△AOD≌△BOC,写出其中相等的角.
A
D
C
B
O
【解析】由全等三角形对应角相等可得:
∠A=∠B,
∠D=∠C,
∠DOA=∠COB.
4.如图,△ABC≌△DEF,∠B=25°,BC=6cm,AC=4cm ,
你能得出△DEF中哪些角的大小,哪些边的长度
A
B
C
D
E
F
因为△DEF≌△ABC,
所以∠E=∠B=25°,
EF=BC=6cm,
DF=AC=4cm.
【解析】
5.如图,一栅栏顶部是由全等的三角形组成的,其中AC=0.2m ,BC=2AC,求BD的长.
A
B
C
D
【解析】
根据题意得
BD=7BC=7×2AC=7×2×0.2
=2.8(m)
1.能够完全重合的两个图形称为全等图形.
2.全等图形的形状和大小都相同,与位置无关.
3.全等三角形的对应边相等,对应角相等.
通过本课时的学习,需要我们掌握:
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
