1.5弹性碰撞与非弹性碰撞(Word版含答案)
文档属性
| 名称 | 1.5弹性碰撞与非弹性碰撞(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-09 00:00:00 | ||
图片预览



文档简介
粤教版(2019)选择性必修一 1.5 弹性碰撞与非弹性碰撞
一、单选题
1.图为两个质量分别为m、M的小球在光滑水平冰面上发生对心正碰前后的x一t图像,则下列说法正确的是( )
A.M:m = 1:3
B.碰撞过程中两小球所受合外力相同
C.碰撞前后质量为m的小球动量的变化量大小为2m
D.两小球发生的是弹性碰撞
2.图所示,质量为m的物块放在质量为M(含挡板)的小车上,物块用细线与小车上的固定挡板相连,被压缩的轻弹簧放在物块与挡板之间,物块随小车一起以大小为v的速度在光滑的水平面上做匀速运动。某时刻,细线断开,物块被轻弹簧弹开,以相对小车大小为v1的水平速度离开小车,此时小车刚好静止,则( )
A. B. C. D.
3.水平冰面上有一固定的竖直挡板,一滑冰运动员面对挡板静止在冰面上,他把一质量为4.0kg的静止物块以大小为5.0m/s的速度沿与挡板垂直的方向推向挡板,运动员获得退行速度;物块与挡板弹性碰撞,速度反向,追上运动员时,运动员又把物块推向挡板,使其再一次以大小为5.0m/s的速度与挡板弹性碰撞。总共经过8次这样推物块后,运动员退行速度的大小大于5.0m/s,反弹的物块不能再追上运动员。不计冰面的摩擦力,该运动员的质量不可能为( )
A.48kg B.53kg C.55kg D.58kg
4.如图所示,质量均为m的木块A、B与轻弹簧相连,置于光滑水平桌面上处于静止状态,与木块A、B完全相同的木块C以速度v0与木块A碰撞并粘在一起,则从木块C与木块A碰撞到弹簧压缩到最短的整个过程中,下列说法正确的是( )
A.木块A、B、C和弹簧组成的系统动量守恒,机械能不守恒
B.木块C与木块A碰撞结束时,木块C的速度为零
C.木块C与木块A碰撞结束时,木块C的速度为
D.弹簧的最大弹性势能等于木块A、B、C和弹簧组成系统的动能减少量
5.矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,质量为m的子弹以速度v水平射向滑块,若射击下层,子弹刚好不射出。若射击上层,则子弹刚好能射进一半厚度,如图所示,上述两种情况相比较,下列说法正确的是( )
A.子弹射击上层时,子弹损失的动能多
B.子弹射击上层时,从射入到共速所经历时间较长
C.子弹射击上层时,系统产生的热量多
D.子弹射击上层时,子弹与上层摩擦力较大
6.北京是全球唯一举办过奥运会和冬奥会的城市。若在冬奥会冰壶比赛中,一蓝色冰壶沿着赛道直线运动,与一个质量材质完全相同的红色冰壶发生正面弹性碰撞。忽略冰壶与冰面间的摩擦力,下列可以准确地表示出两个冰壶动量随时间的变化关系的是( )
A. B.
C. D.
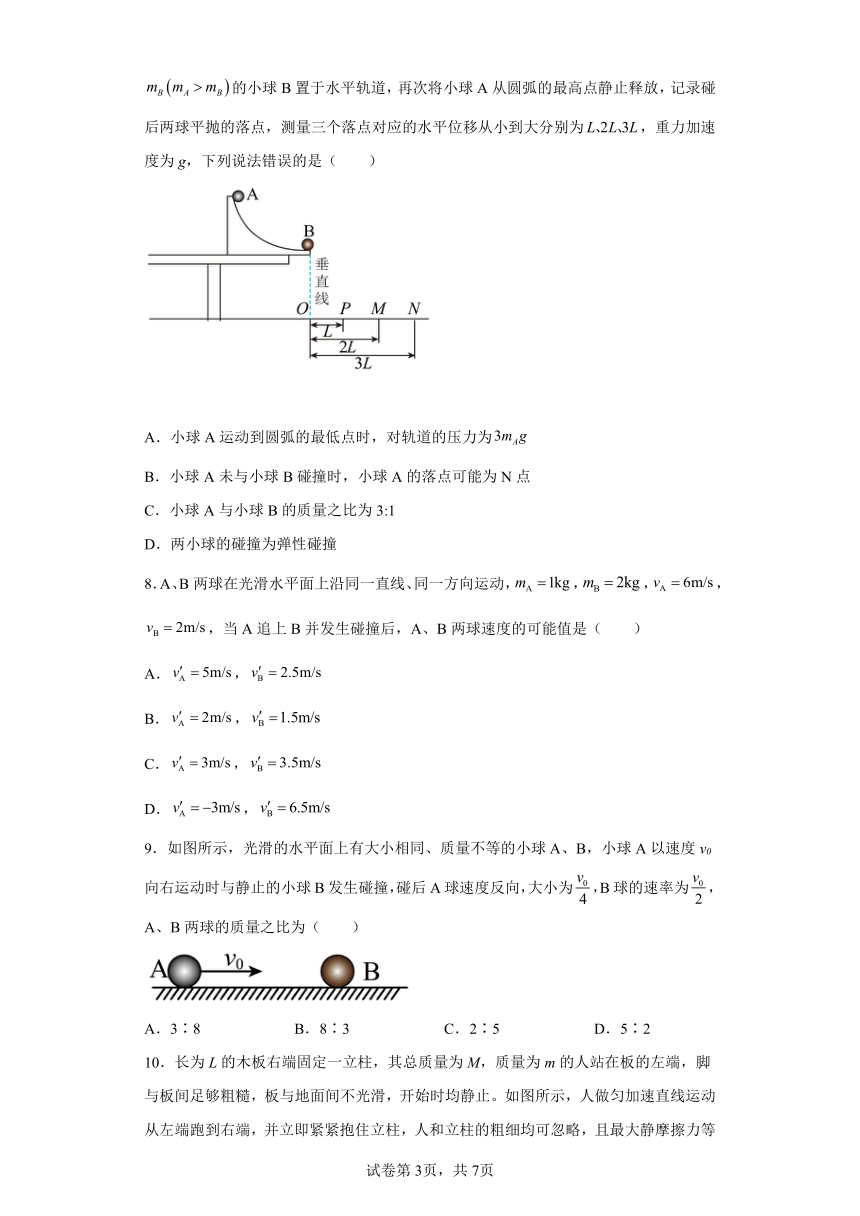
7.如图所示,四分之一光滑圆轨道末端与水平轨道相切,将质量为的小球A从圆弧的最高点静止释放,记录其离开轨道平抛运动落到水平地面上的落点,将质量为的小球B置于水平轨道,再次将小球A从圆弧的最高点静止释放,记录碰后两球平抛的落点,测量三个落点对应的水平位移从小到大分别为,重力加速度为g,下列说法错误的是( )
A.小球A运动到圆弧的最低点时,对轨道的压力为
B.小球A未与小球B碰撞时,小球A的落点可能为N点
C.小球A与小球B的质量之比为3:1
D.两小球的碰撞为弹性碰撞
8.A、B两球在光滑水平面上沿同一直线、同一方向运动,,,,,当A追上B并发生碰撞后,A、B两球速度的可能值是( )
A.,
B.,
C.,
D.,
9.如图所示,光滑的水平面上有大小相同、质量不等的小球A、B,小球A以速度v0向右运动时与静止的小球B发生碰撞,碰后A球速度反向,大小为,B球的速率为,A、B两球的质量之比为( )
A.3∶8 B.8∶3 C.2∶5 D.5∶2
10.长为L的木板右端固定一立柱,其总质量为M,质量为m的人站在板的左端,脚与板间足够粗糙,板与地面间不光滑,开始时均静止。如图所示,人做匀加速直线运动从左端跑到右端,并立即紧紧抱住立柱,人和立柱的粗细均可忽略,且最大静摩擦力等于滑动摩擦力,整个过程木板运动的最大位移为( )
A.,向右
B.,向左
C.,向右
D.与板和地面间的动摩擦因数有关
11.如图甲所示,质量为m的小滑块A以向右的初速度v0滑上静止在光滑水平地面上的平板车B,从滑块A刚滑上平板车B开始计时,它们的速度随时间变化的图象如图乙所示,物块未滑离小车,重力加速度为g,以下说法中正确的是( )
A.滑块A的加速度比平板车B的加速度小
B.平板车B的质量M=3m
C.滑块A与平板车间因摩擦产生的热量为Q=
D.t0时间内摩擦力对小车B做的功为
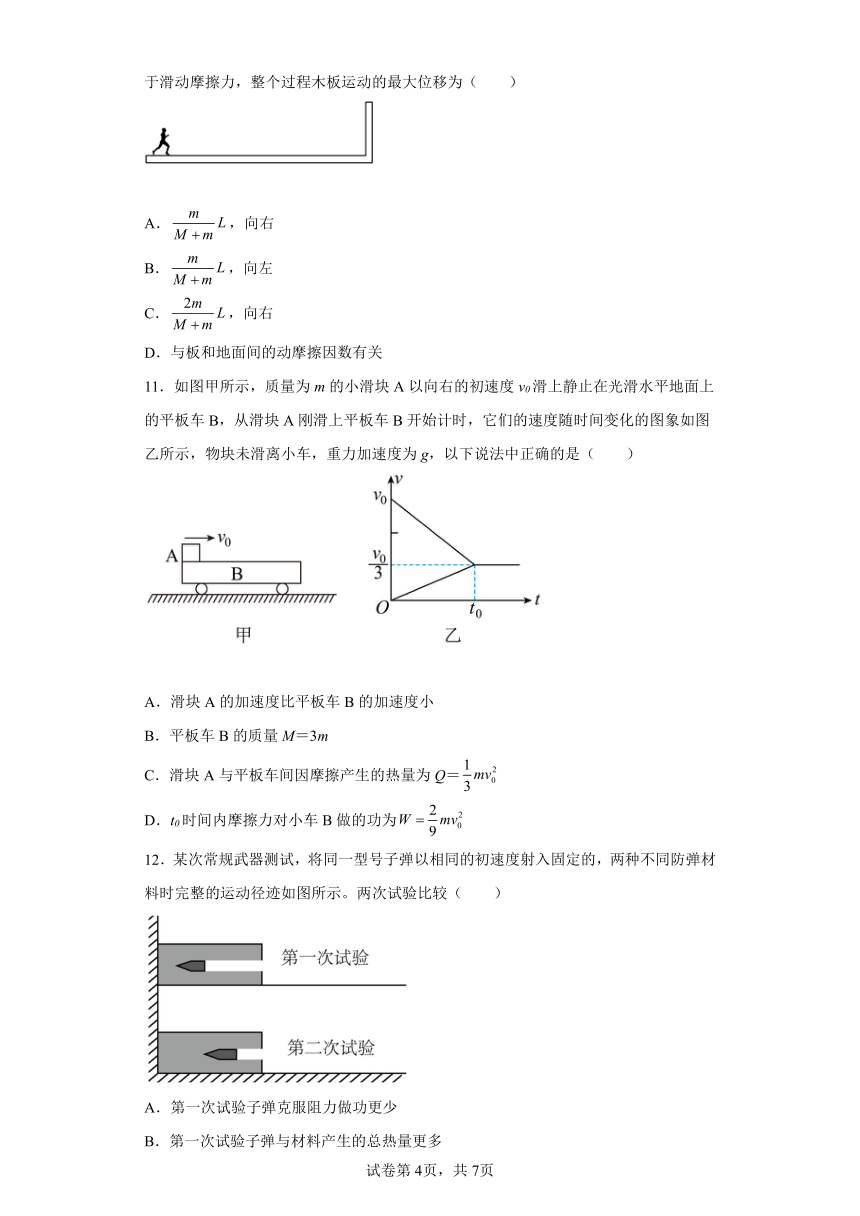
12.某次常规武器测试,将同一型号子弹以相同的初速度射入固定的,两种不同防弹材料时完整的运动径迹如图所示。两次试验比较( )
A.第一次试验子弹克服阻力做功更少
B.第一次试验子弹与材料产生的总热量更多
C.两次试验防弹材料所受冲量相等
D.第二次试验子弹的动量变化量更大
13.如图所示,光滑水平面上有大小相同、质量均为m=3kg的A、B、C三个小球,小球A以速度v0=4m/s向左运动,与静止不动右端有一轻弹簧的小球B发生对心碰撞,压缩弹簧;当A、B速度相等时,B与C恰好相碰并粘接在一起,然后继续运动。假设B和C碰撞过程时间极短,碰撞后小球A与弹簧不粘连,则下列说法正确的是( )
A.弹簧最短时,三个小球共同速度的大小为1m/s
B.从开始到弹簧最短的过程中小球C受到的冲量大小为4N·s
C.从开始到小球A与弹簧分离的过程中整个系统损失的机械能为6J
D.小球B与小球C碰撞之前,小球A、B共同速度的大小为3m/s
14.速度为的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,则碰撞后塑料球与钢球的速度大小之比为( )
A. B. C. D.
15.在光滑水平地面上,有两个质量分别为、的小物体,运动后发生正碰,碰撞时间极短,碰后两物体粘在一起,两物体碰撞前后的图像如图所示。以下判断正确的是( )
A. B.
C.碰撞前后的动量不变 D.碰撞前后两物体的总机械能不变
二、填空题
16.如图所示,两相同的磁铁分别固定在两相同的小车上,水平面光滑,开始两车相向运动,va=3m/s,vb=2m/s,设相互作用时两车不会相碰,则当b车速度为零时,va =________, 方向________;当两车相距最近时,vb=________,方向________.
17.一个木块静止在光滑水平面上,一颗子弹水平射入木块未穿出,当子弹刚好相对木块静止时,木块发生位移为s,设子弹受到木块的阻力大小恒定,子弹射入木块中的深度为d,则s与d的关系为s____d(填大于,等于或小于)
18.在光滑水平面上,A、B小球质量分别为2 kg和1 kg,两个小球分别以0.5m/s和2m/s的速度相向运动,碰撞后两物体粘在一起,则它们的共同速度大小为________m/s,方向_________.
三、解答题
19.如图所示,水平面上有一质量m=1 kg的小车,其右端固定一水平轻质弹簧,弹簧左端连接一质量m0=1 kg的小物块,小物块与小车一起以v0=6 m/s的速度向右运动,与静止在水平面上质量M=4 kg的小球发生正碰,碰后小球的速度v=2 m/s,碰撞时间极短,弹簧始终在弹性限度内,忽略一切摩擦阻力。求:
(1)小车与小球碰撞后瞬间小车的速度v1;
(2)从碰后瞬间到弹簧被压缩至最短的过程中,弹簧弹力对小车的冲量大小。
20.光滑水平面上,质量为1kg的小球A以5m/s的速度向右运动,大小相同的小球B质量为4kg,以0.5m/s的速度向右运动,两者发生正碰,碰撞后小球B以2m/s的速度向右运动,求:
(1)碰后A球的速度v;
(2)碰撞过程中A球对B球的冲量大小I。
21.如图1所示,固定的水平平台上距水平平台右端m处有一木块A(可视为质点),紧靠平台右端的水平地面上放置一与平台等高的水平木板B,木板B上距木板B左端m处固定一轻挡板,挡板右侧和物块C(可视为质点,刚好位于木板B的右端)之间由机关锁定着一个压缩的轻弹簧(弹簧与物块C不拴接)。木块A在水平向右的拉力F作用下由静止开始运动,力F与木块A位移的关系图象如图2所示。木块A刚好与挡板接触不发生碰撞并粘连在一起,此时机关解除锁定,弹簧瞬间弹开,最终木板B的左端与平台右端的距离m(木板B未与平台相碰)。已知木块A、木板B、物块C的质量关系为kg,木块A与平台间的动摩擦因数,木板B与地面间的动摩擦因数,取重力加速度大小m/s2。求:
(1)木块A刚刚滑上木板B时的速度大小;
(2)木块A与木板B上表面间的动摩擦因数;
(3)弹开前弹簧储存的弹性势能。
22.如图1所示是打桩机进行路基打桩的实物情境图,打桩过程情境模型如图2所示,已知打桩机重锤A的质量为m,混凝土钢筋桩B的质量为M,其中M=8m。每一次打桩时,打桩机抬高重锤A,比桩B顶部高出H,然后从静止自由释放,与桩发生时间极短的完全非弹性碰撞后,与桩一起向下运动,设桩受到的阻力f与深度h成正比,即f=kh,其中k=(重力加速度为g,其他阻力忽略不计)。
(1)完成第1次打桩后,试求桩B深入地面下的深度h1;
(2)已知桩B的长度l=3H,试求使桩B刚好全部进入地面下,则要打多少次?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【详解】
A.因x-t图像的斜率等于速度,可知m和M碰前速度分别为v1=4m/s和v2=0;碰后速度分别为v1′=-2m/s和v2′=2m/s,则由动量守恒定律
解得
M:m = 3:1
选项A错误;
B.碰撞过程中两小球只受到它们间的相互作用力,则各自受到的作用力即小球的合外力,它们的合外力大小相等,方向相反,B错误;
C.碰撞前后质量为m的小球动量的变化量大小为
p=(-2m)-4m=6m
选项C错误;
D.两小球碰撞前后的能量为
可知
E = E′
则两小球发生的是弹性碰撞,D正确。
故选D。
2.A
【详解】
当物块离开小车时,小车刚好静止,所以此时物块对地的速度就是v1,对物块和小车组成的系统,由动量守恒
解得
故A正确,BCD错误。
故选A。
3.A
【详解】
设运动员的质量为M,物块质量为m,第一次推物块后,运动员速度大小为v1,第二次推物块后,运动员速度大小为v2…第八次推物块后,运动员速度大小为v8,第一次推物块后,由动量守恒定律知
第二次推物块后由动量守恒定律知
第n次推物块后,由动量守恒定律知
整理得
则代入数据得
, .
总共经过8次这样推物块后反弹的物块不能再追上运动员可知,第7次可以追上第8次追不上即v7<5.0m/s,则M>52kg,v8>5.0m/s,则M<60kg,故选A选项正确,BCD错误。
故选A。
4.A
【详解】
A.木块A、B、C和弹簧组成的系统所受合外力为零,所以系统动量守恒。木块C与A碰撞并粘在一起,此过程系统机械能有损失,故系统机械能不守恒,A正确;
BC.木块C与A碰撞并粘在一起,以木块C与木块A组成的系统为研究对象,取水平向右为正方向,根据动量守恒定律得
解得
即木块C与木块A碰撞结束时,木块C的速度为,BC错误;
D.木块C与A碰撞过程中机械能有损失,之后粘合体在通过弹簧与物块B作用过程中满足动量守恒和机械能守恒,粘合体与物块B达到共速时,弹簧的弹性势能最大,但由于碰撞过程系统机械能有损失,所以弹簧的最大弹性势能小于木块A、B、C和弹簧组成系统的动能减少量,D错误。
故选A。
5.D
【详解】
AC.子弹射入滑块的过程中,将子弹和滑块看成一个整体,合外力为0,动量守恒,所以两种情况后子弹和滑块的速度相同,所以末动能相同,故系统损失的动能一样多,产生的热量一样多,AC错误;
BD.子弹射入上层滑块能进一半厚度,射入下层滑块刚好不射出,说明在上层所受的摩擦力比下层大,根据动量定理可知,两种情况冲量相同,子弹射击上层所受摩擦力大,所以从入射到共速经历时间短,B错误,D正确。
故选D。
6.D
【详解】
设两冰壶的质量均为,蓝冰壶碰撞前的速度为,碰撞后的速度为,红冰壶碰撞后的速度为,两冰壶发生正面弹性碰撞,根据动量守恒定律有
根据能量守恒定理有
联立解得
,
则可知,碰撞后两冰壶速度互换,则ABC错误D正确。
故选D。
7.B
【详解】
A.取圆弧轨道的半径为R,由机械能守恒定律有
由牛顿第二定律得小球A在圆弧的最低点有
联立得小球A运动到圆弧的最低点对轨道的压力为
A正确;
B.小球平抛运动下落的高度相等,平抛运动时间相同,对应的平抛运动的速度可表示为,小球A未与小球B碰撞时,若小球A的落点为N点,由碰撞过程动量守恒有
得
与题意不符,B错误;
C.由以上分析可知,小球A未与小球B碰撞时,小球A的落点为M点,碰后小球A和小球B的落点分别为,由碰撞过程动量守恒有
得
C正确;
D.碰前小球A的动能为
碰后小球A和B动能和为
则两小球的碰撞为弹性碰撞,D正确。
此题选择不正确的选项,故选B。
8.C
【详解】
AB.两球碰撞后A的速度不可能大于B的速度,故A、B均错误;
C.两球碰撞过程,系统不受外力,系统总动量守恒,根据能量守恒定律,碰撞后系统总动能应该小于或者等于碰撞前的系统总动能,碰撞前总动能为22 J,C选项碰后总动能为16.75 J,符合题意,故C正确;
D.D选项满足碰撞过程系统总动量守恒,但是碰后总动能为46.75 J,超出原有的总动能,故D错误。
故选C。
9.C
【详解】
以A、B两球组成的系统为研究对象,两球碰撞过程动量守恒,以A球的初速度方向为正方向,由动量守恒定律得
解得两球的质量之比
故C正确,故ABD错误。
故选C。
10.A
【详解】
B.假设板与地面地面光滑,则人与木板满足动量守恒,设人和立柱相遇时,人的速度大小为v1,木板速度大小为v2,则有
设此过程木板位移为x1,运动时间为t1,由运动学公式有
,
联立上式可得
方向向左,由题知板与地面不光滑,则其向左位移达不到,B错误;
ACD.板与地面不光滑,人与立柱抱住后,会获得向右的共同速度v3,随着板与地面动摩擦因数逐渐增大,木板向左的位移会逐渐减小,进而出现向右的位移。若板与地面间动摩擦因数增加至无穷大,则整个过程木板几乎不动,位移为零。由上述分析可得,当板与地面间动摩擦因数取一个临界值时,木板存在向右的一个最大位移,此临界值恰好能使在人运动过程中,板与地面间达到最大静摩擦力,即木板静止不动。设人与木板间动摩擦因数为μ1,木板与地面间动摩擦因数为μ1,在人运动过程中对木板受力分析则有
人在运动过程中,木板静止不动,则抱住立柱前木板速度,由运动学公式可得人的速度为
人抱住立柱后,由动量守恒定律可得
此后人和木板向右做匀减速运动,设位移为x2,则有
联立上式可得
方向向右,故A正确,CD错误。
故选A。
11.C
【详解】
A.由乙图可知,滑块A、 B的加速度大小分别为
,
所以
故A错误;
B.对A和B在相对滑行的过程中,系统不受外力而动量守恒,有
解得
故B错误;
C.对A和B相对滑动到共速的过程,由能量守恒定律可知,系统损失的动能转化成两者摩擦生热,有
可解得
故C正确;
D.由动能定理可知,摩擦力对B做的功为
故D错误。
故选C。
12.C
【详解】
A.依题意,两次子弹克服阻力做功
可知子弹克服阻力做功相等,故A错误;
B.根据能量守恒,子弹的动能全部转化为子弹与材料的总热量,故试验中产生总热量相等,故B错误;
C.两次试验防弹材料动量始终为0,根据动量定理可知所受冲量相等,均为0,故C正确;
D.子弹的动量变化量为
可知两次试验中子弹的动量变化量相等,故D错误。
故选C。
13.B
【详解】
D.根据动量守恒定律,当小球A、B速度相等时,且与小球C碰撞之前A、B的速度均为v1,则
解得
故D错误;
A.从开始到弹簧最短的过程,对A、B、C系统有
解得
故A错误;
B.从开始到弹簧最短的过程,对小球C,由动量定理有
故B正确;
C.B与C相碰的过程
解得
则从开始到小球A与弹簧分离的过程中整个系统损失的机械能为
故C错误。
故选B。
14.B
【详解】
设塑料球的质量为,碰前速度为,碰后速度为,钢球的质量,碰后速度为,且,又由题意可知,两球发生的是弹性碰撞,由动量守恒得
由能量守恒得
解得
故碰撞后塑料球与钢球的速度大小之比为
故选B。
15.A
【详解】
AB.因图像的斜率等于速度,可知碰撞前两物体的速度分别为6m/s和 - 3m/s,碰后两物体的速度为1.5m/s,则由动量守恒定律
m1v1 + m2v2 = (m1 + m2)v
解得
m1:m2 = 1:1
A正确、B错误;
C.碰撞前后m2的动量分别为
p2 = m2v2 = - 3m2
碰后
p′2 = m2v = 1.5m2
C错误;
D.该碰撞为完全非弹性碰撞,能量损失最大,则碰撞前后两物体的总机械能减小了,D错误。
故选A。
16. 1m/s 向右 0.5m/s 向右
【详解】
(1)以两车组成的系统为研究对象,取a车原来行驶的速度方向为正方向,根据动量守恒定律有: ,
计算得出:,方向水平向右.
(2)当两车的速度相同时,距离最短,设相同的速度为 ,以a的初速度方向为正方向,由动量守恒定律得: ,
计算得出: ,方向水平向右.
综上所述本题答案是: (1). 1m/s (2). 向右 (3). 0.5m/s (4). 向右
17.小于
【详解】
设共速时速度为v,根据动量守恒定律得
设相互作用力为f,对木块运用动能定理得
对子弹运用动能定理得
解得
则s小于d。
18. 方向与B小球速度相同
【详解】
以碰撞前质量为4kg的物体速度方向为正方向,两物体碰撞过程中,由动量守恒定律得:,即:,解得:,方向与B小球速度相同.
【点睛】本题的关键要掌握碰撞过程的基本规律:动量守恒定律,运用动量守恒定律时,要注意规定正方向,用符号表示速度的方向.
19.(1),方向向左;(2)4 N·s
【详解】
(1)小车与小球碰撞过程中,动量守恒,以向右为正方向,根据动量守恒定律有
mv0=Mv+mv1
解得
负号表示碰撞后小车向左运动,
(2)当弹簧被压缩到最短时,设小车的速度大小为v2,根据动量守恒定律有
m0v0+mv1=(m0+m)v2
解得
v2=2 m/s
设碰撞后瞬间到弹簧最短的过程,弹簧弹力对小车的冲量大小为I,根据动量定理有
I=mv2-mv1
解得
I=4 N·s
20.(1)1m/s,方向向左;(2)
【详解】
(1)AB两球碰撞过程,系统动量守恒,取向右为正方向
解得
所以碰后球速度大小为,方向向左。
(2)以B球为研究对象,由
得
解得
21.(1);(2)0.5;(3)
【详解】
(1)由图2结合题意分析可知,当木块A在平台上运动时有外力F作用,力F在平台上对木块A做的功
木块A在平台上运动过程由动能定理有
解得
(2)当木块A在木板上滑行时,对A受力分析,由牛顿第二定律有
对木板B和木块C整体受力分析,由牛顿第二定律有
由题意可知当木块A与挡板接触时二者共速,设木块A在B上滑行的时间为t,有
即
由速度关系有
解得
(3)木块A与挡板接触时,A、B、C共同的速度
弹簧弹开过程中A、B、C动量守恒,有
弹簧弹开过程中根据能量守恒定律有
木板B向左滑行过程中有
解得
22.(1);(2)2 025
【详解】
(1)设重锤A下落与桩B碰撞前的速度为v0,则有
因为重锤A与桩B发生了时间极短的完全非弹性碰撞,设碰撞后的共同速度为v,则有
设第1次打桩,桩B克服阻力所做的功为W1则有
其中
从而解得
另一负解不合实际情况,故舍去。
(2)设要打N次,根据动能定理,有
其中
解得
N=2025
答案第1页,共2页
答案第1页,共2页
一、单选题
1.图为两个质量分别为m、M的小球在光滑水平冰面上发生对心正碰前后的x一t图像,则下列说法正确的是( )
A.M:m = 1:3
B.碰撞过程中两小球所受合外力相同
C.碰撞前后质量为m的小球动量的变化量大小为2m
D.两小球发生的是弹性碰撞
2.图所示,质量为m的物块放在质量为M(含挡板)的小车上,物块用细线与小车上的固定挡板相连,被压缩的轻弹簧放在物块与挡板之间,物块随小车一起以大小为v的速度在光滑的水平面上做匀速运动。某时刻,细线断开,物块被轻弹簧弹开,以相对小车大小为v1的水平速度离开小车,此时小车刚好静止,则( )
A. B. C. D.
3.水平冰面上有一固定的竖直挡板,一滑冰运动员面对挡板静止在冰面上,他把一质量为4.0kg的静止物块以大小为5.0m/s的速度沿与挡板垂直的方向推向挡板,运动员获得退行速度;物块与挡板弹性碰撞,速度反向,追上运动员时,运动员又把物块推向挡板,使其再一次以大小为5.0m/s的速度与挡板弹性碰撞。总共经过8次这样推物块后,运动员退行速度的大小大于5.0m/s,反弹的物块不能再追上运动员。不计冰面的摩擦力,该运动员的质量不可能为( )
A.48kg B.53kg C.55kg D.58kg
4.如图所示,质量均为m的木块A、B与轻弹簧相连,置于光滑水平桌面上处于静止状态,与木块A、B完全相同的木块C以速度v0与木块A碰撞并粘在一起,则从木块C与木块A碰撞到弹簧压缩到最短的整个过程中,下列说法正确的是( )
A.木块A、B、C和弹簧组成的系统动量守恒,机械能不守恒
B.木块C与木块A碰撞结束时,木块C的速度为零
C.木块C与木块A碰撞结束时,木块C的速度为
D.弹簧的最大弹性势能等于木块A、B、C和弹簧组成系统的动能减少量
5.矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,质量为m的子弹以速度v水平射向滑块,若射击下层,子弹刚好不射出。若射击上层,则子弹刚好能射进一半厚度,如图所示,上述两种情况相比较,下列说法正确的是( )
A.子弹射击上层时,子弹损失的动能多
B.子弹射击上层时,从射入到共速所经历时间较长
C.子弹射击上层时,系统产生的热量多
D.子弹射击上层时,子弹与上层摩擦力较大
6.北京是全球唯一举办过奥运会和冬奥会的城市。若在冬奥会冰壶比赛中,一蓝色冰壶沿着赛道直线运动,与一个质量材质完全相同的红色冰壶发生正面弹性碰撞。忽略冰壶与冰面间的摩擦力,下列可以准确地表示出两个冰壶动量随时间的变化关系的是( )
A. B.
C. D.
7.如图所示,四分之一光滑圆轨道末端与水平轨道相切,将质量为的小球A从圆弧的最高点静止释放,记录其离开轨道平抛运动落到水平地面上的落点,将质量为的小球B置于水平轨道,再次将小球A从圆弧的最高点静止释放,记录碰后两球平抛的落点,测量三个落点对应的水平位移从小到大分别为,重力加速度为g,下列说法错误的是( )
A.小球A运动到圆弧的最低点时,对轨道的压力为
B.小球A未与小球B碰撞时,小球A的落点可能为N点
C.小球A与小球B的质量之比为3:1
D.两小球的碰撞为弹性碰撞
8.A、B两球在光滑水平面上沿同一直线、同一方向运动,,,,,当A追上B并发生碰撞后,A、B两球速度的可能值是( )
A.,
B.,
C.,
D.,
9.如图所示,光滑的水平面上有大小相同、质量不等的小球A、B,小球A以速度v0向右运动时与静止的小球B发生碰撞,碰后A球速度反向,大小为,B球的速率为,A、B两球的质量之比为( )
A.3∶8 B.8∶3 C.2∶5 D.5∶2
10.长为L的木板右端固定一立柱,其总质量为M,质量为m的人站在板的左端,脚与板间足够粗糙,板与地面间不光滑,开始时均静止。如图所示,人做匀加速直线运动从左端跑到右端,并立即紧紧抱住立柱,人和立柱的粗细均可忽略,且最大静摩擦力等于滑动摩擦力,整个过程木板运动的最大位移为( )
A.,向右
B.,向左
C.,向右
D.与板和地面间的动摩擦因数有关
11.如图甲所示,质量为m的小滑块A以向右的初速度v0滑上静止在光滑水平地面上的平板车B,从滑块A刚滑上平板车B开始计时,它们的速度随时间变化的图象如图乙所示,物块未滑离小车,重力加速度为g,以下说法中正确的是( )
A.滑块A的加速度比平板车B的加速度小
B.平板车B的质量M=3m
C.滑块A与平板车间因摩擦产生的热量为Q=
D.t0时间内摩擦力对小车B做的功为
12.某次常规武器测试,将同一型号子弹以相同的初速度射入固定的,两种不同防弹材料时完整的运动径迹如图所示。两次试验比较( )
A.第一次试验子弹克服阻力做功更少
B.第一次试验子弹与材料产生的总热量更多
C.两次试验防弹材料所受冲量相等
D.第二次试验子弹的动量变化量更大
13.如图所示,光滑水平面上有大小相同、质量均为m=3kg的A、B、C三个小球,小球A以速度v0=4m/s向左运动,与静止不动右端有一轻弹簧的小球B发生对心碰撞,压缩弹簧;当A、B速度相等时,B与C恰好相碰并粘接在一起,然后继续运动。假设B和C碰撞过程时间极短,碰撞后小球A与弹簧不粘连,则下列说法正确的是( )
A.弹簧最短时,三个小球共同速度的大小为1m/s
B.从开始到弹簧最短的过程中小球C受到的冲量大小为4N·s
C.从开始到小球A与弹簧分离的过程中整个系统损失的机械能为6J
D.小球B与小球C碰撞之前,小球A、B共同速度的大小为3m/s
14.速度为的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,则碰撞后塑料球与钢球的速度大小之比为( )
A. B. C. D.
15.在光滑水平地面上,有两个质量分别为、的小物体,运动后发生正碰,碰撞时间极短,碰后两物体粘在一起,两物体碰撞前后的图像如图所示。以下判断正确的是( )
A. B.
C.碰撞前后的动量不变 D.碰撞前后两物体的总机械能不变
二、填空题
16.如图所示,两相同的磁铁分别固定在两相同的小车上,水平面光滑,开始两车相向运动,va=3m/s,vb=2m/s,设相互作用时两车不会相碰,则当b车速度为零时,va =________, 方向________;当两车相距最近时,vb=________,方向________.
17.一个木块静止在光滑水平面上,一颗子弹水平射入木块未穿出,当子弹刚好相对木块静止时,木块发生位移为s,设子弹受到木块的阻力大小恒定,子弹射入木块中的深度为d,则s与d的关系为s____d(填大于,等于或小于)
18.在光滑水平面上,A、B小球质量分别为2 kg和1 kg,两个小球分别以0.5m/s和2m/s的速度相向运动,碰撞后两物体粘在一起,则它们的共同速度大小为________m/s,方向_________.
三、解答题
19.如图所示,水平面上有一质量m=1 kg的小车,其右端固定一水平轻质弹簧,弹簧左端连接一质量m0=1 kg的小物块,小物块与小车一起以v0=6 m/s的速度向右运动,与静止在水平面上质量M=4 kg的小球发生正碰,碰后小球的速度v=2 m/s,碰撞时间极短,弹簧始终在弹性限度内,忽略一切摩擦阻力。求:
(1)小车与小球碰撞后瞬间小车的速度v1;
(2)从碰后瞬间到弹簧被压缩至最短的过程中,弹簧弹力对小车的冲量大小。
20.光滑水平面上,质量为1kg的小球A以5m/s的速度向右运动,大小相同的小球B质量为4kg,以0.5m/s的速度向右运动,两者发生正碰,碰撞后小球B以2m/s的速度向右运动,求:
(1)碰后A球的速度v;
(2)碰撞过程中A球对B球的冲量大小I。
21.如图1所示,固定的水平平台上距水平平台右端m处有一木块A(可视为质点),紧靠平台右端的水平地面上放置一与平台等高的水平木板B,木板B上距木板B左端m处固定一轻挡板,挡板右侧和物块C(可视为质点,刚好位于木板B的右端)之间由机关锁定着一个压缩的轻弹簧(弹簧与物块C不拴接)。木块A在水平向右的拉力F作用下由静止开始运动,力F与木块A位移的关系图象如图2所示。木块A刚好与挡板接触不发生碰撞并粘连在一起,此时机关解除锁定,弹簧瞬间弹开,最终木板B的左端与平台右端的距离m(木板B未与平台相碰)。已知木块A、木板B、物块C的质量关系为kg,木块A与平台间的动摩擦因数,木板B与地面间的动摩擦因数,取重力加速度大小m/s2。求:
(1)木块A刚刚滑上木板B时的速度大小;
(2)木块A与木板B上表面间的动摩擦因数;
(3)弹开前弹簧储存的弹性势能。
22.如图1所示是打桩机进行路基打桩的实物情境图,打桩过程情境模型如图2所示,已知打桩机重锤A的质量为m,混凝土钢筋桩B的质量为M,其中M=8m。每一次打桩时,打桩机抬高重锤A,比桩B顶部高出H,然后从静止自由释放,与桩发生时间极短的完全非弹性碰撞后,与桩一起向下运动,设桩受到的阻力f与深度h成正比,即f=kh,其中k=(重力加速度为g,其他阻力忽略不计)。
(1)完成第1次打桩后,试求桩B深入地面下的深度h1;
(2)已知桩B的长度l=3H,试求使桩B刚好全部进入地面下,则要打多少次?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【详解】
A.因x-t图像的斜率等于速度,可知m和M碰前速度分别为v1=4m/s和v2=0;碰后速度分别为v1′=-2m/s和v2′=2m/s,则由动量守恒定律
解得
M:m = 3:1
选项A错误;
B.碰撞过程中两小球只受到它们间的相互作用力,则各自受到的作用力即小球的合外力,它们的合外力大小相等,方向相反,B错误;
C.碰撞前后质量为m的小球动量的变化量大小为
p=(-2m)-4m=6m
选项C错误;
D.两小球碰撞前后的能量为
可知
E = E′
则两小球发生的是弹性碰撞,D正确。
故选D。
2.A
【详解】
当物块离开小车时,小车刚好静止,所以此时物块对地的速度就是v1,对物块和小车组成的系统,由动量守恒
解得
故A正确,BCD错误。
故选A。
3.A
【详解】
设运动员的质量为M,物块质量为m,第一次推物块后,运动员速度大小为v1,第二次推物块后,运动员速度大小为v2…第八次推物块后,运动员速度大小为v8,第一次推物块后,由动量守恒定律知
第二次推物块后由动量守恒定律知
第n次推物块后,由动量守恒定律知
整理得
则代入数据得
, .
总共经过8次这样推物块后反弹的物块不能再追上运动员可知,第7次可以追上第8次追不上即v7<5.0m/s,则M>52kg,v8>5.0m/s,则M<60kg,故选A选项正确,BCD错误。
故选A。
4.A
【详解】
A.木块A、B、C和弹簧组成的系统所受合外力为零,所以系统动量守恒。木块C与A碰撞并粘在一起,此过程系统机械能有损失,故系统机械能不守恒,A正确;
BC.木块C与A碰撞并粘在一起,以木块C与木块A组成的系统为研究对象,取水平向右为正方向,根据动量守恒定律得
解得
即木块C与木块A碰撞结束时,木块C的速度为,BC错误;
D.木块C与A碰撞过程中机械能有损失,之后粘合体在通过弹簧与物块B作用过程中满足动量守恒和机械能守恒,粘合体与物块B达到共速时,弹簧的弹性势能最大,但由于碰撞过程系统机械能有损失,所以弹簧的最大弹性势能小于木块A、B、C和弹簧组成系统的动能减少量,D错误。
故选A。
5.D
【详解】
AC.子弹射入滑块的过程中,将子弹和滑块看成一个整体,合外力为0,动量守恒,所以两种情况后子弹和滑块的速度相同,所以末动能相同,故系统损失的动能一样多,产生的热量一样多,AC错误;
BD.子弹射入上层滑块能进一半厚度,射入下层滑块刚好不射出,说明在上层所受的摩擦力比下层大,根据动量定理可知,两种情况冲量相同,子弹射击上层所受摩擦力大,所以从入射到共速经历时间短,B错误,D正确。
故选D。
6.D
【详解】
设两冰壶的质量均为,蓝冰壶碰撞前的速度为,碰撞后的速度为,红冰壶碰撞后的速度为,两冰壶发生正面弹性碰撞,根据动量守恒定律有
根据能量守恒定理有
联立解得
,
则可知,碰撞后两冰壶速度互换,则ABC错误D正确。
故选D。
7.B
【详解】
A.取圆弧轨道的半径为R,由机械能守恒定律有
由牛顿第二定律得小球A在圆弧的最低点有
联立得小球A运动到圆弧的最低点对轨道的压力为
A正确;
B.小球平抛运动下落的高度相等,平抛运动时间相同,对应的平抛运动的速度可表示为,小球A未与小球B碰撞时,若小球A的落点为N点,由碰撞过程动量守恒有
得
与题意不符,B错误;
C.由以上分析可知,小球A未与小球B碰撞时,小球A的落点为M点,碰后小球A和小球B的落点分别为,由碰撞过程动量守恒有
得
C正确;
D.碰前小球A的动能为
碰后小球A和B动能和为
则两小球的碰撞为弹性碰撞,D正确。
此题选择不正确的选项,故选B。
8.C
【详解】
AB.两球碰撞后A的速度不可能大于B的速度,故A、B均错误;
C.两球碰撞过程,系统不受外力,系统总动量守恒,根据能量守恒定律,碰撞后系统总动能应该小于或者等于碰撞前的系统总动能,碰撞前总动能为22 J,C选项碰后总动能为16.75 J,符合题意,故C正确;
D.D选项满足碰撞过程系统总动量守恒,但是碰后总动能为46.75 J,超出原有的总动能,故D错误。
故选C。
9.C
【详解】
以A、B两球组成的系统为研究对象,两球碰撞过程动量守恒,以A球的初速度方向为正方向,由动量守恒定律得
解得两球的质量之比
故C正确,故ABD错误。
故选C。
10.A
【详解】
B.假设板与地面地面光滑,则人与木板满足动量守恒,设人和立柱相遇时,人的速度大小为v1,木板速度大小为v2,则有
设此过程木板位移为x1,运动时间为t1,由运动学公式有
,
联立上式可得
方向向左,由题知板与地面不光滑,则其向左位移达不到,B错误;
ACD.板与地面不光滑,人与立柱抱住后,会获得向右的共同速度v3,随着板与地面动摩擦因数逐渐增大,木板向左的位移会逐渐减小,进而出现向右的位移。若板与地面间动摩擦因数增加至无穷大,则整个过程木板几乎不动,位移为零。由上述分析可得,当板与地面间动摩擦因数取一个临界值时,木板存在向右的一个最大位移,此临界值恰好能使在人运动过程中,板与地面间达到最大静摩擦力,即木板静止不动。设人与木板间动摩擦因数为μ1,木板与地面间动摩擦因数为μ1,在人运动过程中对木板受力分析则有
人在运动过程中,木板静止不动,则抱住立柱前木板速度,由运动学公式可得人的速度为
人抱住立柱后,由动量守恒定律可得
此后人和木板向右做匀减速运动,设位移为x2,则有
联立上式可得
方向向右,故A正确,CD错误。
故选A。
11.C
【详解】
A.由乙图可知,滑块A、 B的加速度大小分别为
,
所以
故A错误;
B.对A和B在相对滑行的过程中,系统不受外力而动量守恒,有
解得
故B错误;
C.对A和B相对滑动到共速的过程,由能量守恒定律可知,系统损失的动能转化成两者摩擦生热,有
可解得
故C正确;
D.由动能定理可知,摩擦力对B做的功为
故D错误。
故选C。
12.C
【详解】
A.依题意,两次子弹克服阻力做功
可知子弹克服阻力做功相等,故A错误;
B.根据能量守恒,子弹的动能全部转化为子弹与材料的总热量,故试验中产生总热量相等,故B错误;
C.两次试验防弹材料动量始终为0,根据动量定理可知所受冲量相等,均为0,故C正确;
D.子弹的动量变化量为
可知两次试验中子弹的动量变化量相等,故D错误。
故选C。
13.B
【详解】
D.根据动量守恒定律,当小球A、B速度相等时,且与小球C碰撞之前A、B的速度均为v1,则
解得
故D错误;
A.从开始到弹簧最短的过程,对A、B、C系统有
解得
故A错误;
B.从开始到弹簧最短的过程,对小球C,由动量定理有
故B正确;
C.B与C相碰的过程
解得
则从开始到小球A与弹簧分离的过程中整个系统损失的机械能为
故C错误。
故选B。
14.B
【详解】
设塑料球的质量为,碰前速度为,碰后速度为,钢球的质量,碰后速度为,且,又由题意可知,两球发生的是弹性碰撞,由动量守恒得
由能量守恒得
解得
故碰撞后塑料球与钢球的速度大小之比为
故选B。
15.A
【详解】
AB.因图像的斜率等于速度,可知碰撞前两物体的速度分别为6m/s和 - 3m/s,碰后两物体的速度为1.5m/s,则由动量守恒定律
m1v1 + m2v2 = (m1 + m2)v
解得
m1:m2 = 1:1
A正确、B错误;
C.碰撞前后m2的动量分别为
p2 = m2v2 = - 3m2
碰后
p′2 = m2v = 1.5m2
C错误;
D.该碰撞为完全非弹性碰撞,能量损失最大,则碰撞前后两物体的总机械能减小了,D错误。
故选A。
16. 1m/s 向右 0.5m/s 向右
【详解】
(1)以两车组成的系统为研究对象,取a车原来行驶的速度方向为正方向,根据动量守恒定律有: ,
计算得出:,方向水平向右.
(2)当两车的速度相同时,距离最短,设相同的速度为 ,以a的初速度方向为正方向,由动量守恒定律得: ,
计算得出: ,方向水平向右.
综上所述本题答案是: (1). 1m/s (2). 向右 (3). 0.5m/s (4). 向右
17.小于
【详解】
设共速时速度为v,根据动量守恒定律得
设相互作用力为f,对木块运用动能定理得
对子弹运用动能定理得
解得
则s小于d。
18. 方向与B小球速度相同
【详解】
以碰撞前质量为4kg的物体速度方向为正方向,两物体碰撞过程中,由动量守恒定律得:,即:,解得:,方向与B小球速度相同.
【点睛】本题的关键要掌握碰撞过程的基本规律:动量守恒定律,运用动量守恒定律时,要注意规定正方向,用符号表示速度的方向.
19.(1),方向向左;(2)4 N·s
【详解】
(1)小车与小球碰撞过程中,动量守恒,以向右为正方向,根据动量守恒定律有
mv0=Mv+mv1
解得
负号表示碰撞后小车向左运动,
(2)当弹簧被压缩到最短时,设小车的速度大小为v2,根据动量守恒定律有
m0v0+mv1=(m0+m)v2
解得
v2=2 m/s
设碰撞后瞬间到弹簧最短的过程,弹簧弹力对小车的冲量大小为I,根据动量定理有
I=mv2-mv1
解得
I=4 N·s
20.(1)1m/s,方向向左;(2)
【详解】
(1)AB两球碰撞过程,系统动量守恒,取向右为正方向
解得
所以碰后球速度大小为,方向向左。
(2)以B球为研究对象,由
得
解得
21.(1);(2)0.5;(3)
【详解】
(1)由图2结合题意分析可知,当木块A在平台上运动时有外力F作用,力F在平台上对木块A做的功
木块A在平台上运动过程由动能定理有
解得
(2)当木块A在木板上滑行时,对A受力分析,由牛顿第二定律有
对木板B和木块C整体受力分析,由牛顿第二定律有
由题意可知当木块A与挡板接触时二者共速,设木块A在B上滑行的时间为t,有
即
由速度关系有
解得
(3)木块A与挡板接触时,A、B、C共同的速度
弹簧弹开过程中A、B、C动量守恒,有
弹簧弹开过程中根据能量守恒定律有
木板B向左滑行过程中有
解得
22.(1);(2)2 025
【详解】
(1)设重锤A下落与桩B碰撞前的速度为v0,则有
因为重锤A与桩B发生了时间极短的完全非弹性碰撞,设碰撞后的共同速度为v,则有
设第1次打桩,桩B克服阻力所做的功为W1则有
其中
从而解得
另一负解不合实际情况,故舍去。
(2)设要打N次,根据动能定理,有
其中
解得
N=2025
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
