八年级数学冀教版下册 19.4坐标与图形的变化 教案
文档属性
| 名称 | 八年级数学冀教版下册 19.4坐标与图形的变化 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 00:00:00 | ||
图片预览

文档简介
第4讲 坐标与图形的变化
1、教学目标
1、能够利用图形的变化与坐标变化之间的关系解决问题;
2. 理解图形平移. 轴对称. 放大或缩小与坐标之间的关系。
二. 知识点梳理
1. 图形的平移与图形上点的坐标变化
平移 平移规律
沿轴平移 在直角坐标系中,对于坐标平面上任意一点P(),将它沿轴的方向向右(或向左)平移个单位长度,相当于这个点的横坐标增加(或减少),纵坐标不变,即点P()平移到点P,其中
沿轴平移 在直角坐标系中,对于坐标平面上任意一点P,将它沿轴的方向向上(或向下)平移个单位长度,相当于这个点的横坐标不变,纵坐标增加(或减少),即点P平移到点P,其中
注意事项
由平移方向和平移距离能确定平移后图形上各点的坐标,由图形平移前后点的坐标能确定图形是如何变化的,图形的平移变化中,点的坐标变化规律是“右加左减,上加下减”。
2、图形的轴对称与图形上点的坐标变化
轴对称 变化规律
关于轴对称 关于轴成轴对称的两个图形,各对应顶点的横坐标相等,纵坐标互为相反数
关于轴对称 关于轴成轴对称的两个图形,各对应顶点的横坐标互为相反数,纵坐标相等
归纳总结
在平面直角坐标系,设点P的坐标为:
(1)如果点P1的坐标是,那么点P1与点P关于轴对称;
(2)如果点P2的坐标是,那么点P2与点P关于y轴对称。
3、图形的伸缩与坐标变化
将一个图形各顶点的横坐标和纵坐标都乘,所得图形的形状不变,各边扩大到原来的倍,且连接各对应顶点的直线相交于一点。
归纳总结:
当图形各顶点的坐标乘时,图形对应边的长扩大到原来的倍,面积扩大为原图形面积的倍;当图形各顶点的坐标乘时,图形对应边的长缩小为原来的,面积缩小为原图形面积的。
3、典型例题
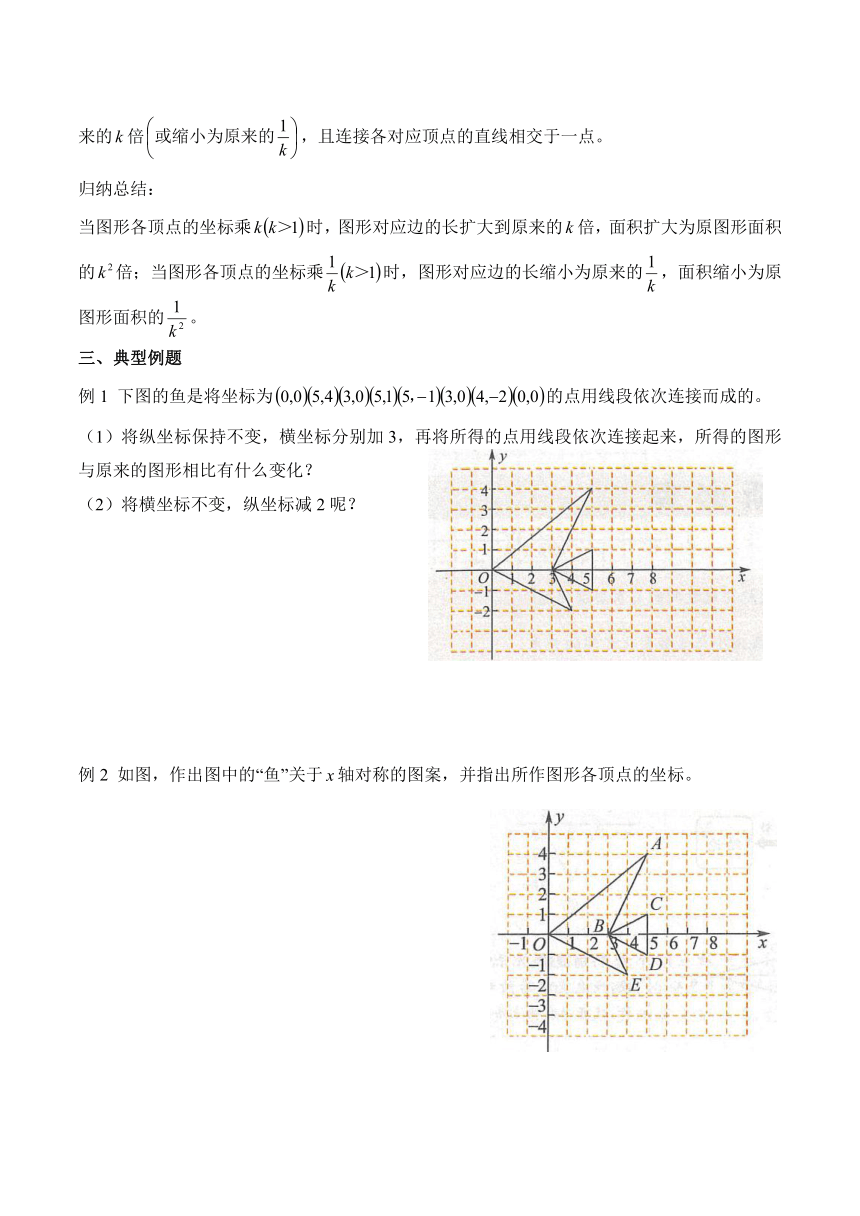
例1 下图的鱼是将坐标为的点用线段依次连接而成的。
(1)将纵坐标保持不变,横坐标分别加3,再将所得的点用线段依次连接起来,所得的图形与原来的图形相比有什么变化?
(2)将横坐标不变,纵坐标减2呢?
例2 如图,作出图中的“鱼”关于轴对称的图案,并指出所作图形各顶点的坐标。
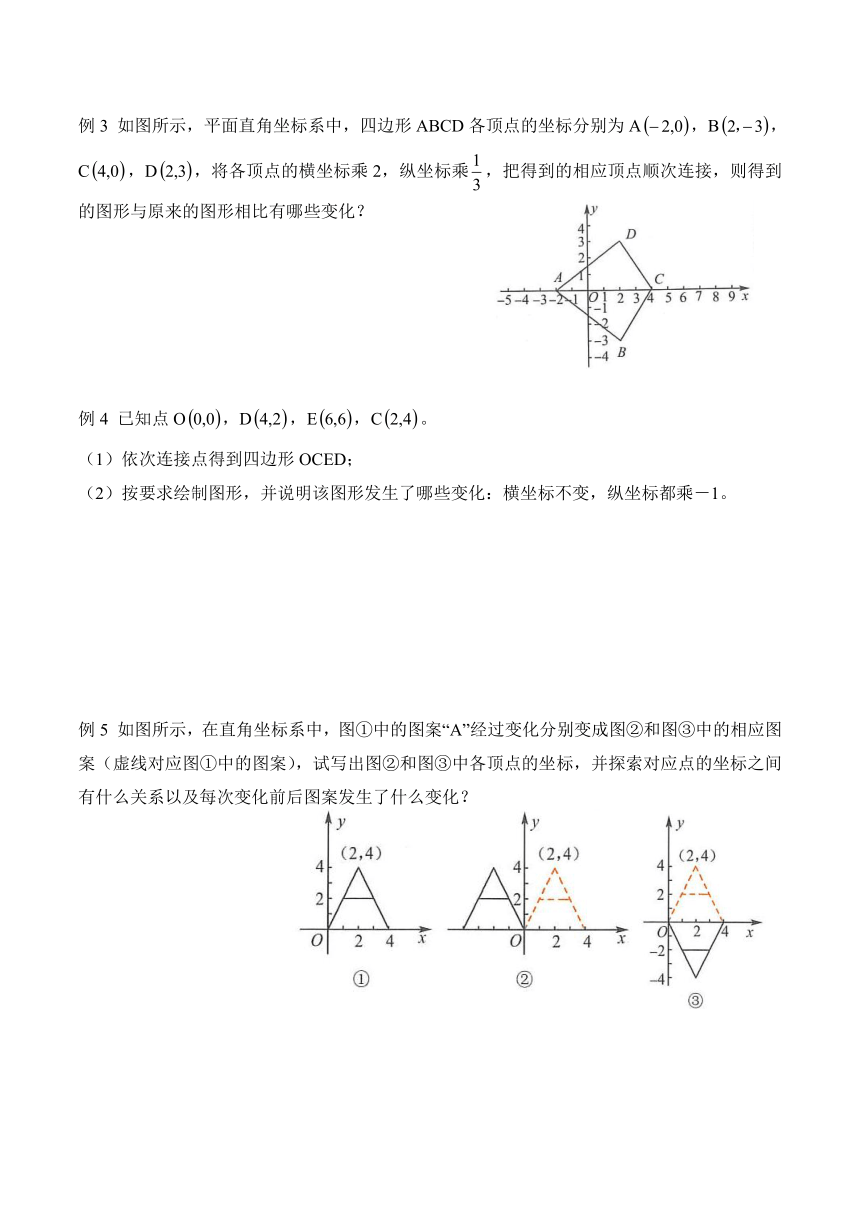
例3 如图所示,平面直角坐标系中,四边形ABCD各顶点的坐标分别为A,B,C,D,将各顶点的横坐标乘2,纵坐标乘,把得到的相应顶点顺次连接,则得到的图形与原来的图形相比有哪些变化?
例4 已知点O,D,E,C。
(1)依次连接点得到四边形OCED;
(2)按要求绘制图形,并说明该图形发生了哪些变化:横坐标不变,纵坐标都乘-1。
例5 如图所示,在直角坐标系中,图①中的图案“A”经过变化分别变成图②和图③中的相应图案(虚线对应图①中的图案),试写出图②和图③中各顶点的坐标,并探索对应点的坐标之间有什么关系以及每次变化前后图案发生了什么变化?
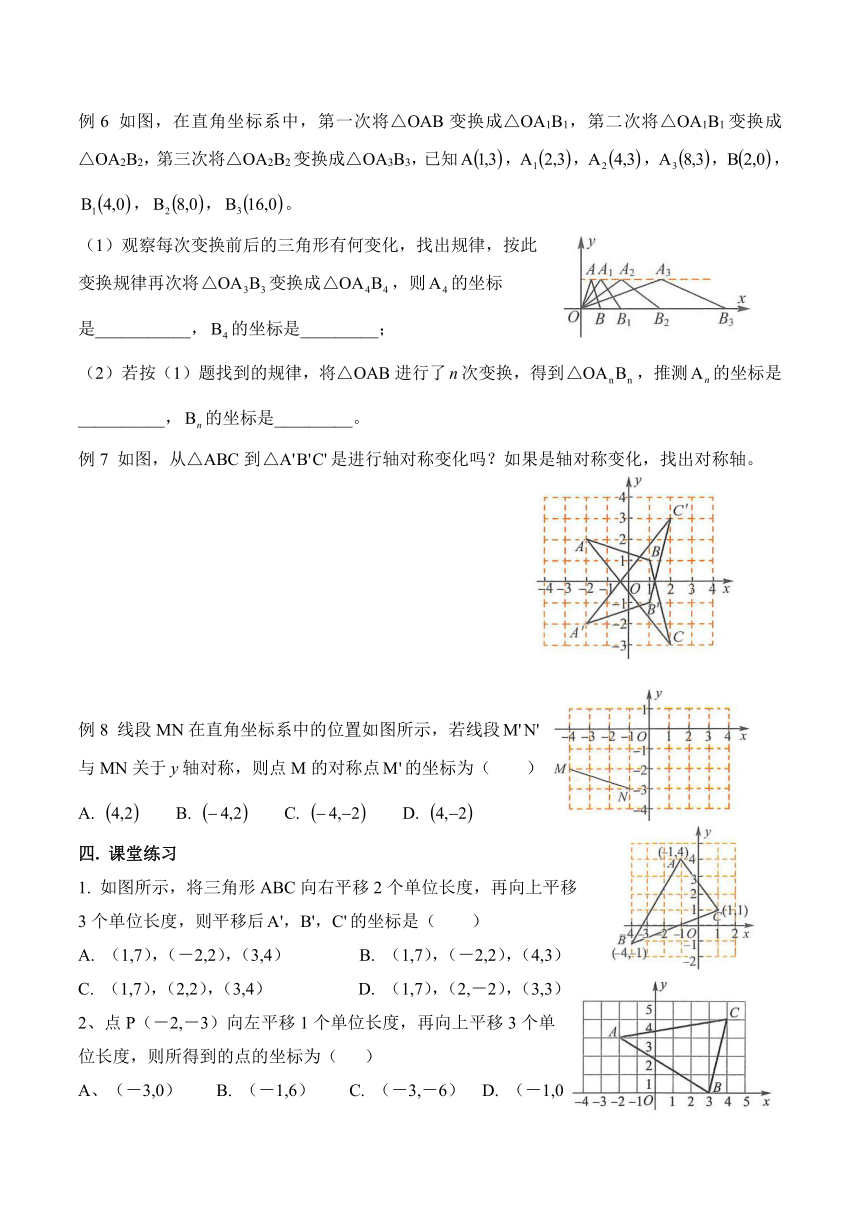
例6 如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知,,,,,,,。
(1)观察每次变换前后的三角形有何变化,找出规律,按此
变换规律再次将变换成,则的坐标
是___________,的坐标是_________;
(2)若按(1)题找到的规律,将△OAB进行了次变换,得到,推测的坐标是__________,的坐标是_________。
例7 如图,从△ABC到是进行轴对称变化吗?如果是轴对称变化,找出对称轴。
例8 线段MN在直角坐标系中的位置如图所示,若线段
与MN关于轴对称,则点M的对称点的坐标为( )
A. B. C. D.
四. 课堂练习
1. 如图所示,将三角形ABC向右平移2个单位长度,再向上平移
3个单位长度,则平移后的坐标是( )
A. (1,7),(-2,2),(3,4) B. (1,7),(-2,2),(4,3)
C. (1,7),(2,2),(3,4) D. (1,7),(2,-2),(3,3)
2、点P(-2,-3)向左平移1个单位长度,再向上平移3个单
位长度,则所得到的点的坐标为( )
A、(-3,0) B. (-1,6) C. (-3,-6) D. (-1,0)
3、如图,如果△与△ABC关于轴对称,那么点A的对称点的坐标为________。
4、如图,在平面直角坐标系中,将点A(-2,3)向右平移3个
单位长度,那么平移后的对应点的坐标是( )
A、(-2,-3) B. (-2,6) C. (1,3) D. (-2,1)
5、如图将三角形向左平移4个单位后,再向下平移2个单位,
则平移后三个顶点的坐标分别是( )
A、(-2,-1)(1,-3)(0,-1) B. (-2,-1)(1,-3)(-1,3)
C. (2,1)(1,-3)(0,3) D. (-2,-1)(0,1)(-1,3)
6、将平面直角坐标系内某图形的各点的纵坐标都乘以-1,横坐标不
变,所得图形与原图形的关系是( )
A、关于轴对称 B. 关于轴对称
C. 关于原点对称 D. 沿轴向下平移1个单位长度
7、直角坐标系中,一个图案上各个点的横坐标和纵坐标分别乘以正数,那么所得的图案与原来的图案相比( )
A、形状不变,边长扩大为原来的倍 B. 图案向右平移了个单位
C. 图案向上平移了个单位 D. 图案沿纵向拉长为倍
8、在平面直角坐标系中,一只青蛙从点A(-1,0)处向右跳2个单位长度,再向上跳2个单位长度到点处,则点的坐标为_________。
9、如图,平行四边形ABCD四个顶点分别是A(-2,-1),B(1,-3),C(4,-1),D(1,1),将平行四边形沿轴负方向平移3个单位,各个顶点的坐标变为多少?将它沿轴正方向平移4个单位呢?分别画出平移后的图形。
10、如图,分别作出△ABC关于轴和轴对称的图形.
11. 已知在直角坐标系中,三角形A OB的各顶点的坐标分别为(2,4),(0,0),(4,0).
(1)将三角形A OB各顶点的坐标都乘2,并在同一直角坐标系中画出图形;
(2)将三角形A OB各顶点的坐标都乘,也在该直角坐标系中画出图形.
12. 如图,长方形A BCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
(1)将长方形各顶点的横. 纵坐标都乘以2,写出各对应点A',B',C' , D'的坐标;顺次连接A ' , B' , C',D',画出相应的图形;
(2)求新长方形与原长方形面积的比;
(3)将长方形A BCD的各顶点的横. 纵坐标都扩大n倍(n为正整数),求新长方形与原长方形的面积的比。
13. 如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3)。
(1)求出△ABC的面积;
(2)在图中作出△ABC关于轴对称的图形△,并写出的坐标。
14. 如图所示,将坐标分别为(1,0),(3,1),(6,0),(8,1),(7,-1),(6,0),(4,-2),(1,0)的点用线段顺次连接起来,再描出点(2,0),就得到鱼的图案。
(1)对于上述各点,纵坐标分别加2,横坐标不变,再将所得的点用线段顺次连接起来,新图形与原图形比较有什么不同?
(2)对于上述各点,纵坐标不变,横坐标分别减去3,将所得的点用线段顺次连接起来,新图形与原图形比较有什么不同?
(3)对于上述各点,纵坐标分别加2,横坐标分别减去3,新图形与原图形比较有什么不同?
15. 在平面直角坐标系中:
(1)分别描出以下各点,A(1,-1),B(1,1),C(2,1),D(0,2),E(-2,1),F(-1,1),G(-1,-1),顺次连接各点得到一个封闭图形,画出该图形。
(2)把A. B. C. D. E. F. G各点的坐标都乘2,写出变化后的各点坐标,描出各点,画出封闭图形。
(3)比较两图,你发现了什么?
五. 课后作业
1、将下图方格纸中上面的图形平移后和下面的图形拼成一个
长方形,那么正确的平移方法是( )
A、先向下移动1格,再向左移动1格
B、先向下移动1格,再向左移动2格
C、先向下移动2格,再向左移动1格
D、先向左移动2格,再向下移动1格
2、如图,将三角形的三个顶点向右平移2个单位长度,再向上
平移3个单位长度,所得的三角形的三个顶点的坐标是( )
A、(2,2)(3,4)(1,7) B. (-2,2)(4,3)(1,7)
C. (2,-2)(3,3)(1,7) D. (-2,2)(3,4)(1,7)
3、如图,点A. B的坐标分别为(2,0),(0,1),若将线段
AB平移至A1B1,则的值为( )
A. 2 B. 3 C. 4 D. 5
4. 在平面直角坐标系中有△A BC,将△ABC各顶点的横. 纵坐标乘以2,得到△A'B'C',△ A'B'C'与△ABC相比( )
A.形状改变,大小改变 B.形状不变,大小不变
C.形状改变,大小不变 D.形状不变,大小改变
5. 将P(-4,3)先向左平移2个单位,再向下平移2个单位得到,则点的坐标为______。
6. 将△ABC向右平移5个单位,再向上平移6个单位后A点的坐标为(4,7),则平移前A点的坐标为_________。
7. 将点P(m+2,6)向右平移一个单位得到点(4,6),则m的值等于_______。
8. 将△ABC各顶点的横. 纵坐标乘以得到△DEF,则△ABC与△DEF的对应边之比为_______,面积之比为_________。
9、等边△A BC的一个顶点的坐标为B(1,0),顶点C与顶点B关于轴对称,则顶点A的坐标为_________。
10、△ABC在如图所示的直角坐标系中,则△A BC关于轴对称的△A'B'C'中,点A' ,B' ,C'的坐标分别是_______,________,_________。
11. (1)在直角坐标系中,描出点A(-2,1),B(-3,-5),C(0,4),画出以A. B. C为顶点的三角形;
(2)将△ABC向右平移,使顶点A移到点(1,1)处,画出平移后的△,写出
的坐标;
(3)△ABC和△的对应顶点坐标之间有什么关系?如果点M(m,n)在边AB上,点是点M的对应点,试写出点的坐标。
12. 已知△ABC的三个顶点的坐标如下表:
(1)将此表补充完整,并在直角坐标系中画出△A BC和△A'B'C';
(2)观察△A BC与△A'B'C',写出有关这两个三角形关系的一个正确结论.
() ()
A(2,1) (4,2)
B(4,3) ( )
C(5,1) ( )
13. 如图,已知△ABC位于平面直角坐标系内,且三个顶点均在正方形网格的顶点上.
(1)将△A BC顶点A ,B,C的横. 纵坐标分别乘以-2,依次作为点A1,B1,C1,的横. 纵坐标,画出△A 1B1C1;
(2)将△A 1B1C1,向下平移2个单位,再向右平移2个单位,得到△A2B2C2,画出△A 2B2C2,并写出B1的对应点B2的坐标.
B1(,2)
B(0,1) A1(3,)
A(2,0)
A(2,0)
1、教学目标
1、能够利用图形的变化与坐标变化之间的关系解决问题;
2. 理解图形平移. 轴对称. 放大或缩小与坐标之间的关系。
二. 知识点梳理
1. 图形的平移与图形上点的坐标变化
平移 平移规律
沿轴平移 在直角坐标系中,对于坐标平面上任意一点P(),将它沿轴的方向向右(或向左)平移个单位长度,相当于这个点的横坐标增加(或减少),纵坐标不变,即点P()平移到点P,其中
沿轴平移 在直角坐标系中,对于坐标平面上任意一点P,将它沿轴的方向向上(或向下)平移个单位长度,相当于这个点的横坐标不变,纵坐标增加(或减少),即点P平移到点P,其中
注意事项
由平移方向和平移距离能确定平移后图形上各点的坐标,由图形平移前后点的坐标能确定图形是如何变化的,图形的平移变化中,点的坐标变化规律是“右加左减,上加下减”。
2、图形的轴对称与图形上点的坐标变化
轴对称 变化规律
关于轴对称 关于轴成轴对称的两个图形,各对应顶点的横坐标相等,纵坐标互为相反数
关于轴对称 关于轴成轴对称的两个图形,各对应顶点的横坐标互为相反数,纵坐标相等
归纳总结
在平面直角坐标系,设点P的坐标为:
(1)如果点P1的坐标是,那么点P1与点P关于轴对称;
(2)如果点P2的坐标是,那么点P2与点P关于y轴对称。
3、图形的伸缩与坐标变化
将一个图形各顶点的横坐标和纵坐标都乘,所得图形的形状不变,各边扩大到原来的倍,且连接各对应顶点的直线相交于一点。
归纳总结:
当图形各顶点的坐标乘时,图形对应边的长扩大到原来的倍,面积扩大为原图形面积的倍;当图形各顶点的坐标乘时,图形对应边的长缩小为原来的,面积缩小为原图形面积的。
3、典型例题
例1 下图的鱼是将坐标为的点用线段依次连接而成的。
(1)将纵坐标保持不变,横坐标分别加3,再将所得的点用线段依次连接起来,所得的图形与原来的图形相比有什么变化?
(2)将横坐标不变,纵坐标减2呢?
例2 如图,作出图中的“鱼”关于轴对称的图案,并指出所作图形各顶点的坐标。
例3 如图所示,平面直角坐标系中,四边形ABCD各顶点的坐标分别为A,B,C,D,将各顶点的横坐标乘2,纵坐标乘,把得到的相应顶点顺次连接,则得到的图形与原来的图形相比有哪些变化?
例4 已知点O,D,E,C。
(1)依次连接点得到四边形OCED;
(2)按要求绘制图形,并说明该图形发生了哪些变化:横坐标不变,纵坐标都乘-1。
例5 如图所示,在直角坐标系中,图①中的图案“A”经过变化分别变成图②和图③中的相应图案(虚线对应图①中的图案),试写出图②和图③中各顶点的坐标,并探索对应点的坐标之间有什么关系以及每次变化前后图案发生了什么变化?
例6 如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知,,,,,,,。
(1)观察每次变换前后的三角形有何变化,找出规律,按此
变换规律再次将变换成,则的坐标
是___________,的坐标是_________;
(2)若按(1)题找到的规律,将△OAB进行了次变换,得到,推测的坐标是__________,的坐标是_________。
例7 如图,从△ABC到是进行轴对称变化吗?如果是轴对称变化,找出对称轴。
例8 线段MN在直角坐标系中的位置如图所示,若线段
与MN关于轴对称,则点M的对称点的坐标为( )
A. B. C. D.
四. 课堂练习
1. 如图所示,将三角形ABC向右平移2个单位长度,再向上平移
3个单位长度,则平移后的坐标是( )
A. (1,7),(-2,2),(3,4) B. (1,7),(-2,2),(4,3)
C. (1,7),(2,2),(3,4) D. (1,7),(2,-2),(3,3)
2、点P(-2,-3)向左平移1个单位长度,再向上平移3个单
位长度,则所得到的点的坐标为( )
A、(-3,0) B. (-1,6) C. (-3,-6) D. (-1,0)
3、如图,如果△与△ABC关于轴对称,那么点A的对称点的坐标为________。
4、如图,在平面直角坐标系中,将点A(-2,3)向右平移3个
单位长度,那么平移后的对应点的坐标是( )
A、(-2,-3) B. (-2,6) C. (1,3) D. (-2,1)
5、如图将三角形向左平移4个单位后,再向下平移2个单位,
则平移后三个顶点的坐标分别是( )
A、(-2,-1)(1,-3)(0,-1) B. (-2,-1)(1,-3)(-1,3)
C. (2,1)(1,-3)(0,3) D. (-2,-1)(0,1)(-1,3)
6、将平面直角坐标系内某图形的各点的纵坐标都乘以-1,横坐标不
变,所得图形与原图形的关系是( )
A、关于轴对称 B. 关于轴对称
C. 关于原点对称 D. 沿轴向下平移1个单位长度
7、直角坐标系中,一个图案上各个点的横坐标和纵坐标分别乘以正数,那么所得的图案与原来的图案相比( )
A、形状不变,边长扩大为原来的倍 B. 图案向右平移了个单位
C. 图案向上平移了个单位 D. 图案沿纵向拉长为倍
8、在平面直角坐标系中,一只青蛙从点A(-1,0)处向右跳2个单位长度,再向上跳2个单位长度到点处,则点的坐标为_________。
9、如图,平行四边形ABCD四个顶点分别是A(-2,-1),B(1,-3),C(4,-1),D(1,1),将平行四边形沿轴负方向平移3个单位,各个顶点的坐标变为多少?将它沿轴正方向平移4个单位呢?分别画出平移后的图形。
10、如图,分别作出△ABC关于轴和轴对称的图形.
11. 已知在直角坐标系中,三角形A OB的各顶点的坐标分别为(2,4),(0,0),(4,0).
(1)将三角形A OB各顶点的坐标都乘2,并在同一直角坐标系中画出图形;
(2)将三角形A OB各顶点的坐标都乘,也在该直角坐标系中画出图形.
12. 如图,长方形A BCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
(1)将长方形各顶点的横. 纵坐标都乘以2,写出各对应点A',B',C' , D'的坐标;顺次连接A ' , B' , C',D',画出相应的图形;
(2)求新长方形与原长方形面积的比;
(3)将长方形A BCD的各顶点的横. 纵坐标都扩大n倍(n为正整数),求新长方形与原长方形的面积的比。
13. 如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3)。
(1)求出△ABC的面积;
(2)在图中作出△ABC关于轴对称的图形△,并写出的坐标。
14. 如图所示,将坐标分别为(1,0),(3,1),(6,0),(8,1),(7,-1),(6,0),(4,-2),(1,0)的点用线段顺次连接起来,再描出点(2,0),就得到鱼的图案。
(1)对于上述各点,纵坐标分别加2,横坐标不变,再将所得的点用线段顺次连接起来,新图形与原图形比较有什么不同?
(2)对于上述各点,纵坐标不变,横坐标分别减去3,将所得的点用线段顺次连接起来,新图形与原图形比较有什么不同?
(3)对于上述各点,纵坐标分别加2,横坐标分别减去3,新图形与原图形比较有什么不同?
15. 在平面直角坐标系中:
(1)分别描出以下各点,A(1,-1),B(1,1),C(2,1),D(0,2),E(-2,1),F(-1,1),G(-1,-1),顺次连接各点得到一个封闭图形,画出该图形。
(2)把A. B. C. D. E. F. G各点的坐标都乘2,写出变化后的各点坐标,描出各点,画出封闭图形。
(3)比较两图,你发现了什么?
五. 课后作业
1、将下图方格纸中上面的图形平移后和下面的图形拼成一个
长方形,那么正确的平移方法是( )
A、先向下移动1格,再向左移动1格
B、先向下移动1格,再向左移动2格
C、先向下移动2格,再向左移动1格
D、先向左移动2格,再向下移动1格
2、如图,将三角形的三个顶点向右平移2个单位长度,再向上
平移3个单位长度,所得的三角形的三个顶点的坐标是( )
A、(2,2)(3,4)(1,7) B. (-2,2)(4,3)(1,7)
C. (2,-2)(3,3)(1,7) D. (-2,2)(3,4)(1,7)
3、如图,点A. B的坐标分别为(2,0),(0,1),若将线段
AB平移至A1B1,则的值为( )
A. 2 B. 3 C. 4 D. 5
4. 在平面直角坐标系中有△A BC,将△ABC各顶点的横. 纵坐标乘以2,得到△A'B'C',△ A'B'C'与△ABC相比( )
A.形状改变,大小改变 B.形状不变,大小不变
C.形状改变,大小不变 D.形状不变,大小改变
5. 将P(-4,3)先向左平移2个单位,再向下平移2个单位得到,则点的坐标为______。
6. 将△ABC向右平移5个单位,再向上平移6个单位后A点的坐标为(4,7),则平移前A点的坐标为_________。
7. 将点P(m+2,6)向右平移一个单位得到点(4,6),则m的值等于_______。
8. 将△ABC各顶点的横. 纵坐标乘以得到△DEF,则△ABC与△DEF的对应边之比为_______,面积之比为_________。
9、等边△A BC的一个顶点的坐标为B(1,0),顶点C与顶点B关于轴对称,则顶点A的坐标为_________。
10、△ABC在如图所示的直角坐标系中,则△A BC关于轴对称的△A'B'C'中,点A' ,B' ,C'的坐标分别是_______,________,_________。
11. (1)在直角坐标系中,描出点A(-2,1),B(-3,-5),C(0,4),画出以A. B. C为顶点的三角形;
(2)将△ABC向右平移,使顶点A移到点(1,1)处,画出平移后的△,写出
的坐标;
(3)△ABC和△的对应顶点坐标之间有什么关系?如果点M(m,n)在边AB上,点是点M的对应点,试写出点的坐标。
12. 已知△ABC的三个顶点的坐标如下表:
(1)将此表补充完整,并在直角坐标系中画出△A BC和△A'B'C';
(2)观察△A BC与△A'B'C',写出有关这两个三角形关系的一个正确结论.
() ()
A(2,1) (4,2)
B(4,3) ( )
C(5,1) ( )
13. 如图,已知△ABC位于平面直角坐标系内,且三个顶点均在正方形网格的顶点上.
(1)将△A BC顶点A ,B,C的横. 纵坐标分别乘以-2,依次作为点A1,B1,C1,的横. 纵坐标,画出△A 1B1C1;
(2)将△A 1B1C1,向下平移2个单位,再向右平移2个单位,得到△A2B2C2,画出△A 2B2C2,并写出B1的对应点B2的坐标.
B1(,2)
B(0,1) A1(3,)
A(2,0)
A(2,0)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
