八年级数学冀教版下册 9.3坐标与图形的位置 教案
文档属性
| 名称 | 八年级数学冀教版下册 9.3坐标与图形的位置 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 00:00:00 | ||
图片预览


文档简介
第3讲 坐标与图形的位置
1、教学目标
1、能用点的坐标描述图形的形状;
2. 理解点的坐标与位置的对应关系。
二. 知识点梳理
1. 建立适当的直角坐标系
(1)根据已知条件建立坐标系的常用方法:
①以某已知点为原点. ②以图形中某线段所在直线为轴(或轴).
③以已知线段中点为原点. ④以两直线交点为原点.
⑤利用图形的轴对称性把对称轴定为轴等.
总之,原则就是使计算简便.
(2)建立不同的直角坐标系,同一图形的顶点坐标也不同,应根据具体情况建立适当的直角坐标系.
注意事项:建立平面直角坐标系没有固定的模式,可根据具体情况灵活选择,但要尽量选择能比较简捷地表示图形上某些特殊点的坐标的方法.
2、用坐标描述图形形状
说明一个简单的平面图形的形状,就是设法说明图形中各个关键点(如顶点. 圆心等)的位置,可先建立平面直角坐标系,在所建坐标系中求出关键点的坐标.
总结:把图形放在直角坐标系中,图形上的点就有了相应的坐标,利用坐标可以描述图形的形状和大小。
注意事项:用坐标描述图形形状的依据是:坐标平面上的点与有序实数对是一一对应的,所
以描述的图形是唯一的.
3、典型例题
例1 如图所示,在Rt△ABC中,BC=4,∠ACB=90°,∠A=30°,以B为坐标原点,BC所在直线为轴建立平面直角坐标系。
(1)写出点A的坐标;
(2)还可以怎样建立平面直角坐标系,试着写一写各顶点的坐标。
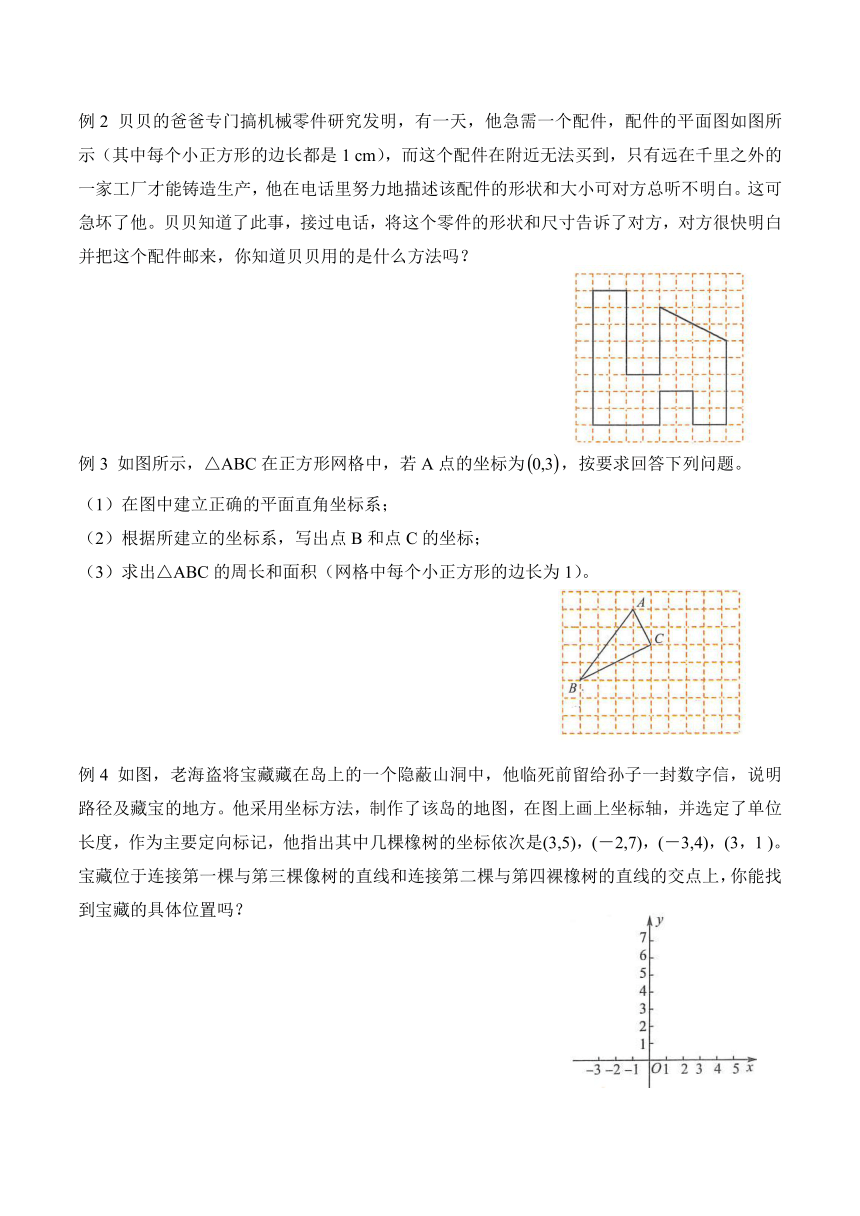
例2 贝贝的爸爸专门搞机械零件研究发明,有一天,他急需一个配件,配件的平面图如图所示(其中每个小正方形的边长都是1 cm),而这个配件在附近无法买到,只有远在千里之外的一家工厂才能铸造生产,他在电话里努力地描述该配件的形状和大小可对方总听不明白。这可急坏了他。贝贝知道了此事,接过电话,将这个零件的形状和尺寸告诉了对方,对方很快明白并把这个配件邮来,你知道贝贝用的是什么方法吗?
例3 如图所示,△ABC在正方形网格中,若A点的坐标为,按要求回答下列问题。
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)求出△ABC的周长和面积(网格中每个小正方形的边长为1)。
例4 如图,老海盗将宝藏藏在岛上的一个隐蔽山洞中,他临死前留给孙子一封数字信,说明路径及藏宝的地方。他采用坐标方法,制作了该岛的地图,在图上画上坐标轴,并选定了单位长度,作为主要定向标记,他指出其中几棵橡树的坐标依次是(3,5),(-2,7),(-3,4),(3,1 )。宝藏位于连接第一棵与第三棵像树的直线和连接第二棵与第四裸橡树的直线的交点上,你能找到宝藏的具体位置吗?
例5 已知等边三角形ABC的边长为,顶点B,C在轴上(点B在点C左侧),顶点A在轴上,求各顶点的坐标。
4、课堂练习
1、如图是湖南邵阳几个旅游景点的大致位置示意图,如果用
表示新宁崀山的位置,用表示隆回花瑶的位置,那么城步南山
的位置可以表示为( )
A、(2,1) B. (0,1) C. (-2,-1) D. (-2,1)
2、如图是永州市几个主要景点示意图,根据图中的信息可确定九
嶷山的中心位置点C的坐标为__________。
3、点A(0,2),点B(0,-4),点C在轴上,如果△ABC的
面积为15,则点C的坐标为__________。
4、已知正方形三个顶点的坐标分别为(-1,1),(2,1),(-1,4),则第四个顶
点的坐标是( )
A.(2,-2) B.(一1,-2) C.(2,4) D.(2,-4)
5、如图,已知等腰三角形ABC中,顶点A的坐标是(),顶点B的
坐标是(0,-2),BC∥轴,则顶点C的坐标是________。
6、徐浩同学准备把如图所示的一张“探宝路线图”通过电话告诉李林同学,请你帮助设计一种方法,把“探宝路线图”清楚地告诉对方.
7. 小明的生日快要到了,小军决定送给他一件小礼物,他告诉小明,已将礼物藏在学校体育场,但具体地点忘了,只知道坐标是C(8,8),并且告诉小明体育场内的两个标志点A,B的坐标分别是(-2,-3)和(2,-3),如何确定直角坐标系让小明找到小军藏礼物的地点C呢?
8、如图,在Rt△ A BC中,∠C=90°,AC=BC,AB=4,试建立适当的直角坐标系,并写出各顶点的坐标.
9. 如图是某市部分地区的示意图,请你建立适当的平面直角坐标系,并写出图中各地点相应的坐标.
10. 某校八年级(一)班周末组织学生进行创新素质实践活动,参观一些景点和设施。为了便于确定方位,带队老师如图建立了平面直角坐标系。(横轴和纵轴均为小正方形的边所在直线,网格中每个小正方形的边长为1个单位长度)
(1)若在带队老师建立的平面直角坐标系中,网球场的
坐标为(-5,0),请你在图中画出这个平面直角坐标系。
(2)根据(1)中建立的平面直角坐标系,指出其他景
点和设施的坐标。
5、课后作业
1、如图,点A的坐标为(2,2),若点P在x轴的正半轴上,且△A OP
是等腰三角形,则点P的坐标不可能为( )
A.(2,0) B. (4,0) C.(2,0) D.(3,0)
2. 一个长方形在平面直角坐标系中,三个顶点的坐标分别为(-2,-1),(-2,3),(4,-1),则第四个顶点的坐标是( )
A.(3,2) B. (4,2) C.(3,3) D.(4,3)
3. 已知点A ,B的坐标分别为(2,0),(2,4),以点A,B,P为顶点的三角形与△A BO全等,写出一个符合条件的点P的坐标___________。
4. 如图,已知等边△ABC,点A在坐标原点,点B的坐标为(6,0),
则点C的坐标为__________。
5. 陈颖同学要在电话中告诉同学如图所示的图形,为了描述清楚,她使用了与本节有关的知识,你能猜到她用的是什么方法吗 请详细叙述她的方法.
6. 如图,这是某市部分简图,请建立适当的平面直角坐标系,分别写出各地的坐标.
7. 如图,在△ABC中,已知A B=6 , A C=BC=5,建立适当的平面直角坐标系,把△A BC的各顶点的坐标写出来.
8. 如图,草房的地基AB长15米,房檐CD的长为20米,门宽EF为6米,CD到地面的距离为18米,请你建立适当的平面直角坐标系并写出点A ,B,C,,D,E,F的坐标.
9. 已知:在平面直角坐标系中,△ABC的边AB在轴上,A点坐标为(-2,0),且AB=3 , C点的坐标为(2,4).
(1)画出符合条件的三角形A BC,写出B点的坐标;
(2)求三角形ABC的面积.
C
A B
1、教学目标
1、能用点的坐标描述图形的形状;
2. 理解点的坐标与位置的对应关系。
二. 知识点梳理
1. 建立适当的直角坐标系
(1)根据已知条件建立坐标系的常用方法:
①以某已知点为原点. ②以图形中某线段所在直线为轴(或轴).
③以已知线段中点为原点. ④以两直线交点为原点.
⑤利用图形的轴对称性把对称轴定为轴等.
总之,原则就是使计算简便.
(2)建立不同的直角坐标系,同一图形的顶点坐标也不同,应根据具体情况建立适当的直角坐标系.
注意事项:建立平面直角坐标系没有固定的模式,可根据具体情况灵活选择,但要尽量选择能比较简捷地表示图形上某些特殊点的坐标的方法.
2、用坐标描述图形形状
说明一个简单的平面图形的形状,就是设法说明图形中各个关键点(如顶点. 圆心等)的位置,可先建立平面直角坐标系,在所建坐标系中求出关键点的坐标.
总结:把图形放在直角坐标系中,图形上的点就有了相应的坐标,利用坐标可以描述图形的形状和大小。
注意事项:用坐标描述图形形状的依据是:坐标平面上的点与有序实数对是一一对应的,所
以描述的图形是唯一的.
3、典型例题
例1 如图所示,在Rt△ABC中,BC=4,∠ACB=90°,∠A=30°,以B为坐标原点,BC所在直线为轴建立平面直角坐标系。
(1)写出点A的坐标;
(2)还可以怎样建立平面直角坐标系,试着写一写各顶点的坐标。
例2 贝贝的爸爸专门搞机械零件研究发明,有一天,他急需一个配件,配件的平面图如图所示(其中每个小正方形的边长都是1 cm),而这个配件在附近无法买到,只有远在千里之外的一家工厂才能铸造生产,他在电话里努力地描述该配件的形状和大小可对方总听不明白。这可急坏了他。贝贝知道了此事,接过电话,将这个零件的形状和尺寸告诉了对方,对方很快明白并把这个配件邮来,你知道贝贝用的是什么方法吗?
例3 如图所示,△ABC在正方形网格中,若A点的坐标为,按要求回答下列问题。
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)求出△ABC的周长和面积(网格中每个小正方形的边长为1)。
例4 如图,老海盗将宝藏藏在岛上的一个隐蔽山洞中,他临死前留给孙子一封数字信,说明路径及藏宝的地方。他采用坐标方法,制作了该岛的地图,在图上画上坐标轴,并选定了单位长度,作为主要定向标记,他指出其中几棵橡树的坐标依次是(3,5),(-2,7),(-3,4),(3,1 )。宝藏位于连接第一棵与第三棵像树的直线和连接第二棵与第四裸橡树的直线的交点上,你能找到宝藏的具体位置吗?
例5 已知等边三角形ABC的边长为,顶点B,C在轴上(点B在点C左侧),顶点A在轴上,求各顶点的坐标。
4、课堂练习
1、如图是湖南邵阳几个旅游景点的大致位置示意图,如果用
表示新宁崀山的位置,用表示隆回花瑶的位置,那么城步南山
的位置可以表示为( )
A、(2,1) B. (0,1) C. (-2,-1) D. (-2,1)
2、如图是永州市几个主要景点示意图,根据图中的信息可确定九
嶷山的中心位置点C的坐标为__________。
3、点A(0,2),点B(0,-4),点C在轴上,如果△ABC的
面积为15,则点C的坐标为__________。
4、已知正方形三个顶点的坐标分别为(-1,1),(2,1),(-1,4),则第四个顶
点的坐标是( )
A.(2,-2) B.(一1,-2) C.(2,4) D.(2,-4)
5、如图,已知等腰三角形ABC中,顶点A的坐标是(),顶点B的
坐标是(0,-2),BC∥轴,则顶点C的坐标是________。
6、徐浩同学准备把如图所示的一张“探宝路线图”通过电话告诉李林同学,请你帮助设计一种方法,把“探宝路线图”清楚地告诉对方.
7. 小明的生日快要到了,小军决定送给他一件小礼物,他告诉小明,已将礼物藏在学校体育场,但具体地点忘了,只知道坐标是C(8,8),并且告诉小明体育场内的两个标志点A,B的坐标分别是(-2,-3)和(2,-3),如何确定直角坐标系让小明找到小军藏礼物的地点C呢?
8、如图,在Rt△ A BC中,∠C=90°,AC=BC,AB=4,试建立适当的直角坐标系,并写出各顶点的坐标.
9. 如图是某市部分地区的示意图,请你建立适当的平面直角坐标系,并写出图中各地点相应的坐标.
10. 某校八年级(一)班周末组织学生进行创新素质实践活动,参观一些景点和设施。为了便于确定方位,带队老师如图建立了平面直角坐标系。(横轴和纵轴均为小正方形的边所在直线,网格中每个小正方形的边长为1个单位长度)
(1)若在带队老师建立的平面直角坐标系中,网球场的
坐标为(-5,0),请你在图中画出这个平面直角坐标系。
(2)根据(1)中建立的平面直角坐标系,指出其他景
点和设施的坐标。
5、课后作业
1、如图,点A的坐标为(2,2),若点P在x轴的正半轴上,且△A OP
是等腰三角形,则点P的坐标不可能为( )
A.(2,0) B. (4,0) C.(2,0) D.(3,0)
2. 一个长方形在平面直角坐标系中,三个顶点的坐标分别为(-2,-1),(-2,3),(4,-1),则第四个顶点的坐标是( )
A.(3,2) B. (4,2) C.(3,3) D.(4,3)
3. 已知点A ,B的坐标分别为(2,0),(2,4),以点A,B,P为顶点的三角形与△A BO全等,写出一个符合条件的点P的坐标___________。
4. 如图,已知等边△ABC,点A在坐标原点,点B的坐标为(6,0),
则点C的坐标为__________。
5. 陈颖同学要在电话中告诉同学如图所示的图形,为了描述清楚,她使用了与本节有关的知识,你能猜到她用的是什么方法吗 请详细叙述她的方法.
6. 如图,这是某市部分简图,请建立适当的平面直角坐标系,分别写出各地的坐标.
7. 如图,在△ABC中,已知A B=6 , A C=BC=5,建立适当的平面直角坐标系,把△A BC的各顶点的坐标写出来.
8. 如图,草房的地基AB长15米,房檐CD的长为20米,门宽EF为6米,CD到地面的距离为18米,请你建立适当的平面直角坐标系并写出点A ,B,C,,D,E,F的坐标.
9. 已知:在平面直角坐标系中,△ABC的边AB在轴上,A点坐标为(-2,0),且AB=3 , C点的坐标为(2,4).
(1)画出符合条件的三角形A BC,写出B点的坐标;
(2)求三角形ABC的面积.
C
A B
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
