湘教版数学七年级下册 4.6 两条平行线间的距离 课件(共21张PPT)
文档属性
| 名称 | 湘教版数学七年级下册 4.6 两条平行线间的距离 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 774.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 14:35:55 | ||
图片预览



文档简介
(共24张PPT)
第4章 相交线与平行线
4.6 两条平行线间的距离
学习目标
1.掌握公垂线段的概念及其性质;
2.会求平行线段的距离. (重点)
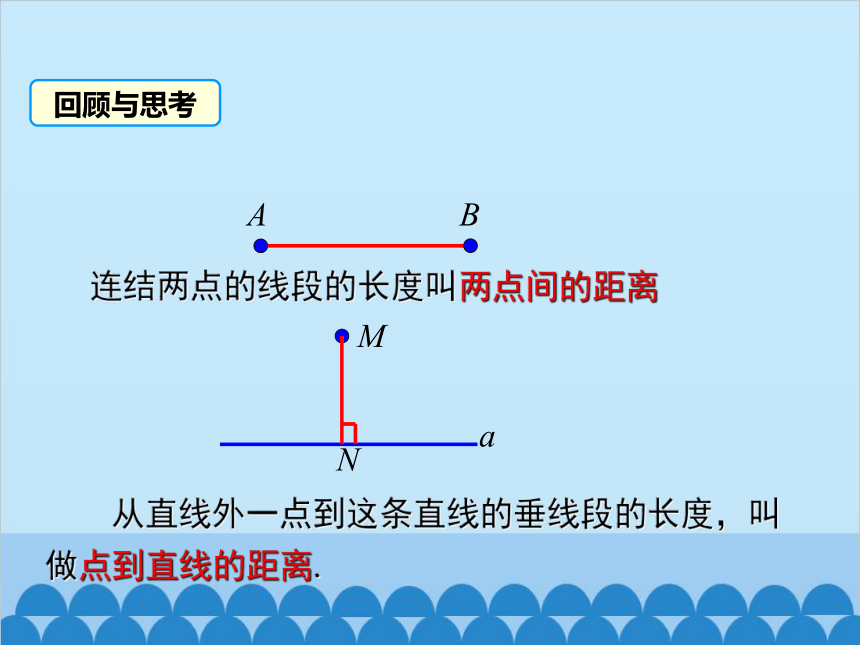
A
B
连结两点的线段的长度叫两点间的距离
M
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
N
a
回顾与思考
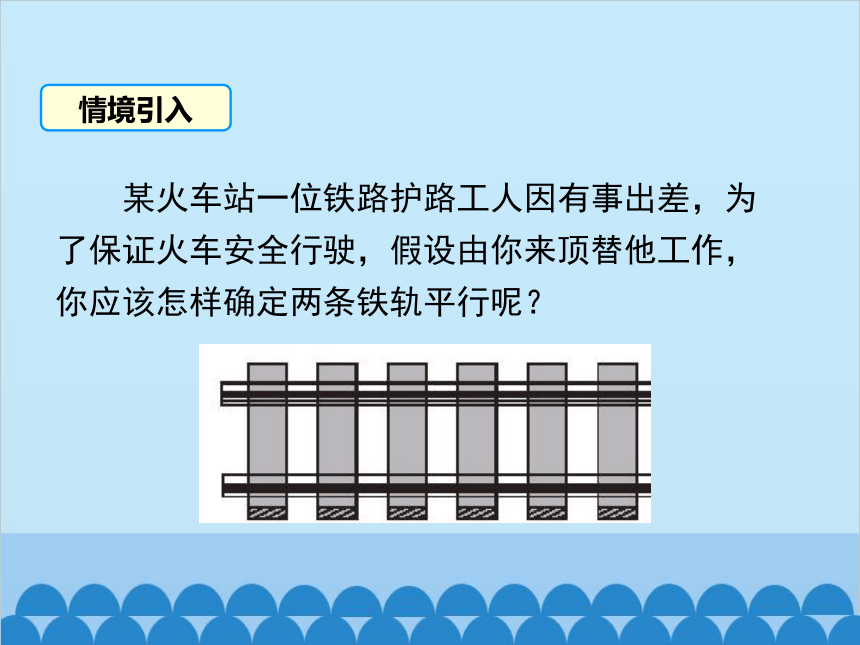
某火车站一位铁路护路工人因有事出差,为了保证火车安全行驶,假设由你来顶替他工作,你应该怎样确定两条铁轨平行呢?
情境引入
活动1:请各位同学用直尺量一量自己的数学课本,它的宽度是多少?
你的直尺与课本的两边成什么角度?量在课本的哪个位置?大家量得的结果是一样的吗?
可以把直尺放在课本上任何一个位置,但必须保持直尺与课本的两边互相垂直,量得的结果是一样的.
两条平行线间的距离
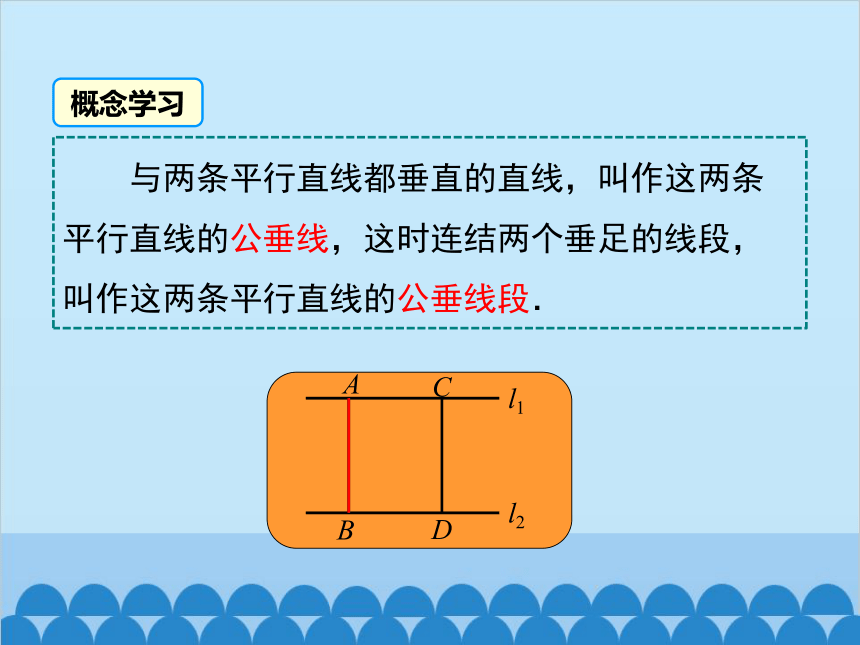
A
B
C
D
l1
l2
与两条平行直线都垂直的直线,叫作这两条平行直线的公垂线,这时连结两个垂足的线段,叫作这两条平行直线的公垂线段.
概念学习
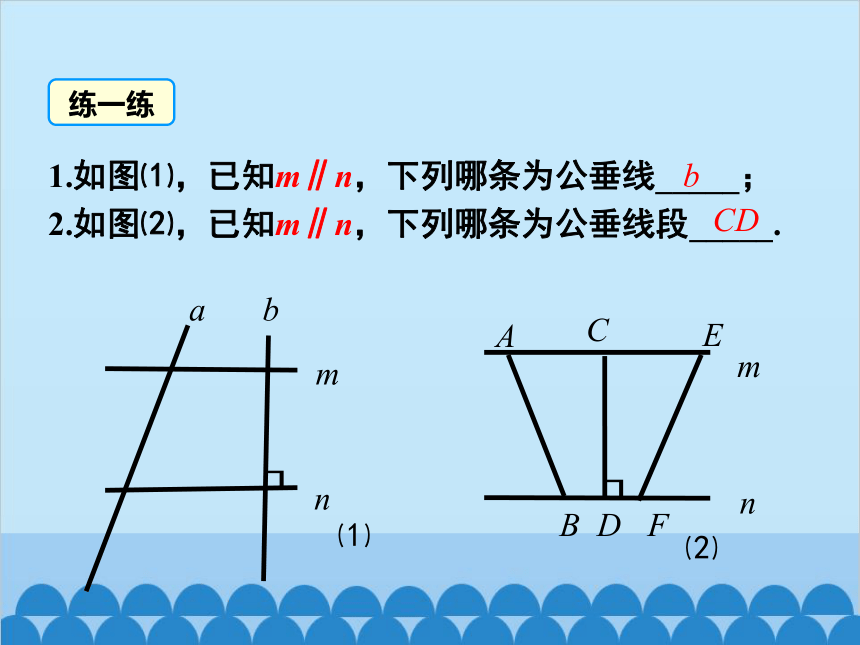
1.如图⑴,已知m∥n,下列哪条为公垂线_____;
2.如图⑵,已知m∥n,下列哪条为公垂线段_____.
m
n
m
n
a
b
A
B
E
C
D
F
┒
┒
b
CD
⑴
⑵
练一练
C
D
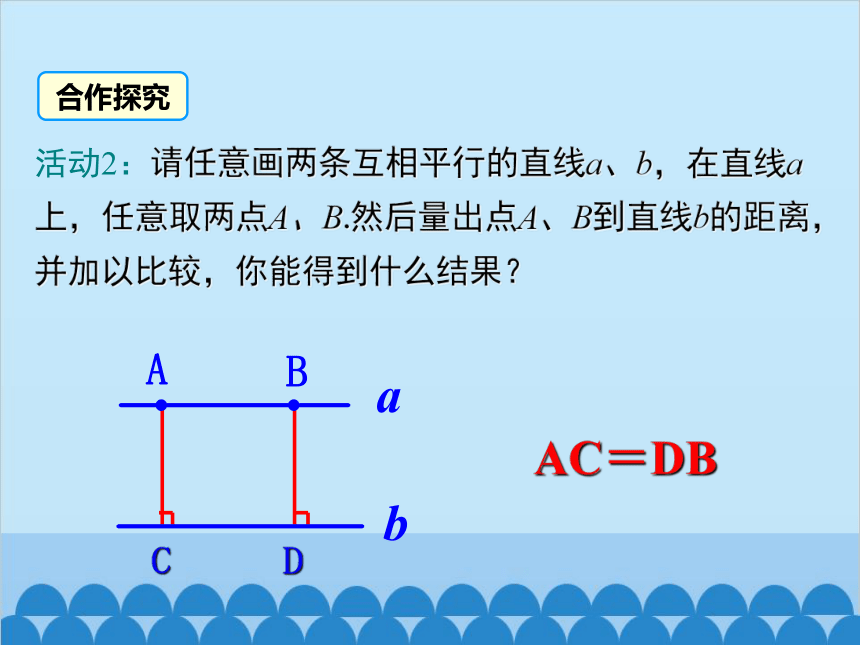
活动2:请任意画两条互相平行的直线a、b,在直线a上,任意取两点A、B.然后量出点A、B到直线b的距离,并加以比较,你能得到什么结果?
AC=DB
合作探究
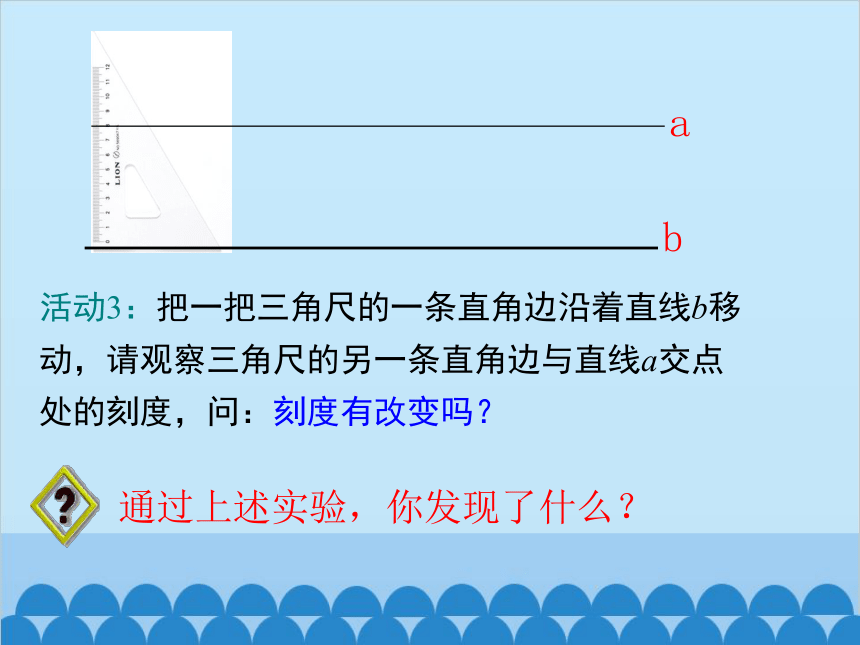
活动3:把一把三角尺的一条直角边沿着直线b移动,请观察三角尺的另一条直角边与直线a交点处的刻度,问:刻度有改变吗?
a
b
通过上述实验,你发现了什么?
两条平行线的所有公垂线段都 .
相等
几何语言:
∵a∥b,AC⊥b,BD⊥b
∴AC=BD
C
D
结论:两条平行线的公垂线段的长度叫做两条平行线间的距离.
归纳总结
如图,设l1//l2,A,B分别为l1,l2上的任意点,连结线段AB,再过A作AC⊥l2,垂足为C,则AC是l1,l2之间的公垂线段,AB是l1,l2之间的斜线段.因为AC,AB又分别是A点到l2的垂线段和斜线段,所以AC两平行线上各取一点连经而成的所有线段中,公垂线段最短.
A
B
C
l1
l2
思考:你可以证明这个猜想是否正确吗?
例1 如图,设a,b,c是三条互相平行的直线.已知a与b的距离为5厘米,b与c的距离为2厘米,求a与c的距离.
在a上任其一点A,过A作AC⊥a,分别与b,c相交于B,C两点则AB,BC,AC分别表示a与b,b与c,a与c的公垂线段.
AC=AB+BC=5+2=7.
A
b
c
B
C
a
5厘米
2厘米
解:
因此a与c的距离是7厘米.
典例精析
(1)如图1,
∵AB=5cm, BC=2cm,
∴AC=7cm
A
B
C
变式:设a、b、c是三条互相平行的直线,已知a与b的距离为5cm,b与c 的距离为2cm,求a与c的距离.
解:有两种情况
图1
a
b
c
a
c
b
A
B
C
图2
(2)如图2 ,
∵AB=5cm, BC=2cm, ∴AC=3cm.
例2:如图,已知AD//BC,判断 与 是否相等,并说明理由.
解:∵AD∥BC
∴△ABC与△DBC的高相等
∵ △ABC与△DBC的底都是BC
∴ △ABC与△DBC是同底等高
∴S△ABC=S△DBC
练一练:如图,MN//AB,P,Q为直线MN上的任意两点,三角形PAB和三角形QAB的面积有什么关系?为什么?
△PAB与△QAB面积相等
∵ MN∥AB,
∴ PM⊥AB ,QN⊥AB
∴ PM=QN,
∴ S△PAB=S△QAB
解:
A
B
M
N
Q
P
M
N
2.点P,M分别在直线AB和直线CD上,且AB∥CD,点P到CD的距离为5cm,则点M到AB的距离为( )
A.大于5 cm B.小于5 cm
C.5 cm D.不确定
1.两平行线的公垂线段有多少条?( )
A.1 B.2
C.无数条 D.一条也没有
C
C
3.如图,a⊥c,b⊥c,c交a,b于A、B两点,d交AB于C、D两点,且d与c不平行,则AB CD(填“>”、“=”、“<”)
(第3题图)
4.如图,长方形ABCD的宽AD的长度是2cm,点P到AB的距离是1.6cm,那么点P到CD的距离是______.
(第4题图)
<
3.6cm
6.已知a∥b∥c,a与b之间的距离为3cm,b与c之间的距离为4cm,则a与c之间的距离为 cm.
5.如图,已知直线MN∥PQ,BC=4cm,若三角形ABC的面积为6cm ,则平行线MN,PQ的距离是 cm.
3
7或1
7.如图是山坡上两棵树,你能量出他们之间的距离吗
如图1,MN∥AB, P、Q为直线MN上的任意两点,ΔPAB和ΔQAB的面积相等吗?为什么?
M P Q N
2.如图2,MN∥AB, P是MN上的一动点,P沿MN的方向每次移动1cm,当它移动10cm 时得到ΔP1AB,那么ΔP1AB的面积是多少?
A B
图1
M P N
P1
A B
图2
a cm2
拓展提升
相等
a cm2
两条平行线的距离
概念
性质
公垂线,公垂线段,
平行线间的距离
两条平行线的公垂线段都相等
第4章 相交线与平行线
4.6 两条平行线间的距离
学习目标
1.掌握公垂线段的概念及其性质;
2.会求平行线段的距离. (重点)
A
B
连结两点的线段的长度叫两点间的距离
M
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
N
a
回顾与思考
某火车站一位铁路护路工人因有事出差,为了保证火车安全行驶,假设由你来顶替他工作,你应该怎样确定两条铁轨平行呢?
情境引入
活动1:请各位同学用直尺量一量自己的数学课本,它的宽度是多少?
你的直尺与课本的两边成什么角度?量在课本的哪个位置?大家量得的结果是一样的吗?
可以把直尺放在课本上任何一个位置,但必须保持直尺与课本的两边互相垂直,量得的结果是一样的.
两条平行线间的距离
A
B
C
D
l1
l2
与两条平行直线都垂直的直线,叫作这两条平行直线的公垂线,这时连结两个垂足的线段,叫作这两条平行直线的公垂线段.
概念学习
1.如图⑴,已知m∥n,下列哪条为公垂线_____;
2.如图⑵,已知m∥n,下列哪条为公垂线段_____.
m
n
m
n
a
b
A
B
E
C
D
F
┒
┒
b
CD
⑴
⑵
练一练
C
D
活动2:请任意画两条互相平行的直线a、b,在直线a上,任意取两点A、B.然后量出点A、B到直线b的距离,并加以比较,你能得到什么结果?
AC=DB
合作探究
活动3:把一把三角尺的一条直角边沿着直线b移动,请观察三角尺的另一条直角边与直线a交点处的刻度,问:刻度有改变吗?
a
b
通过上述实验,你发现了什么?
两条平行线的所有公垂线段都 .
相等
几何语言:
∵a∥b,AC⊥b,BD⊥b
∴AC=BD
C
D
结论:两条平行线的公垂线段的长度叫做两条平行线间的距离.
归纳总结
如图,设l1//l2,A,B分别为l1,l2上的任意点,连结线段AB,再过A作AC⊥l2,垂足为C,则AC是l1,l2之间的公垂线段,AB是l1,l2之间的斜线段.因为AC,AB又分别是A点到l2的垂线段和斜线段,所以AC
A
B
C
l1
l2
思考:你可以证明这个猜想是否正确吗?
例1 如图,设a,b,c是三条互相平行的直线.已知a与b的距离为5厘米,b与c的距离为2厘米,求a与c的距离.
在a上任其一点A,过A作AC⊥a,分别与b,c相交于B,C两点则AB,BC,AC分别表示a与b,b与c,a与c的公垂线段.
AC=AB+BC=5+2=7.
A
b
c
B
C
a
5厘米
2厘米
解:
因此a与c的距离是7厘米.
典例精析
(1)如图1,
∵AB=5cm, BC=2cm,
∴AC=7cm
A
B
C
变式:设a、b、c是三条互相平行的直线,已知a与b的距离为5cm,b与c 的距离为2cm,求a与c的距离.
解:有两种情况
图1
a
b
c
a
c
b
A
B
C
图2
(2)如图2 ,
∵AB=5cm, BC=2cm, ∴AC=3cm.
例2:如图,已知AD//BC,判断 与 是否相等,并说明理由.
解:∵AD∥BC
∴△ABC与△DBC的高相等
∵ △ABC与△DBC的底都是BC
∴ △ABC与△DBC是同底等高
∴S△ABC=S△DBC
练一练:如图,MN//AB,P,Q为直线MN上的任意两点,三角形PAB和三角形QAB的面积有什么关系?为什么?
△PAB与△QAB面积相等
∵ MN∥AB,
∴ PM⊥AB ,QN⊥AB
∴ PM=QN,
∴ S△PAB=S△QAB
解:
A
B
M
N
Q
P
M
N
2.点P,M分别在直线AB和直线CD上,且AB∥CD,点P到CD的距离为5cm,则点M到AB的距离为( )
A.大于5 cm B.小于5 cm
C.5 cm D.不确定
1.两平行线的公垂线段有多少条?( )
A.1 B.2
C.无数条 D.一条也没有
C
C
3.如图,a⊥c,b⊥c,c交a,b于A、B两点,d交AB于C、D两点,且d与c不平行,则AB CD(填“>”、“=”、“<”)
(第3题图)
4.如图,长方形ABCD的宽AD的长度是2cm,点P到AB的距离是1.6cm,那么点P到CD的距离是______.
(第4题图)
<
3.6cm
6.已知a∥b∥c,a与b之间的距离为3cm,b与c之间的距离为4cm,则a与c之间的距离为 cm.
5.如图,已知直线MN∥PQ,BC=4cm,若三角形ABC的面积为6cm ,则平行线MN,PQ的距离是 cm.
3
7或1
7.如图是山坡上两棵树,你能量出他们之间的距离吗
如图1,MN∥AB, P、Q为直线MN上的任意两点,ΔPAB和ΔQAB的面积相等吗?为什么?
M P Q N
2.如图2,MN∥AB, P是MN上的一动点,P沿MN的方向每次移动1cm,当它移动10cm 时得到ΔP1AB,那么ΔP1AB的面积是多少?
A B
图1
M P N
P1
A B
图2
a cm2
拓展提升
相等
a cm2
两条平行线的距离
概念
性质
公垂线,公垂线段,
平行线间的距离
两条平行线的公垂线段都相等
