冀教版七年级上册数学 1.5有理数的加法 课件(共38张PPT)
文档属性
| 名称 | 冀教版七年级上册数学 1.5有理数的加法 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 242.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 16:53:43 | ||
图片预览







文档简介
(共38张PPT)
1.5 有理数的加法
知识与能力
1.经历探索有理数加法法则的过程,理解有理数加法的意义,理解并掌握有理数加法的法则;
2.应用有理数加法法则进行准确运算.
教学目标
过程与方法
1.通过有理数加法的学习,学习化归的意识、数形结合和分类的思想方法,培养观察、比较和概括的思维能力。
2.能够由特殊到一般,总结出有理数的加法法则,培养一定的归纳能力及语言表达能力。
教学目标
情感态度与价值观
体会在总结有理数加法法则的过程中与他人合作、交流的重要性,并且意识到数学与现实生活是紧密相连的.
教学目标
重点
有理数加法法则.
难点
异号两数相加的法则.
教学重难点
小刚在一条东西向的跑道上,先走了30米,又走了20米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
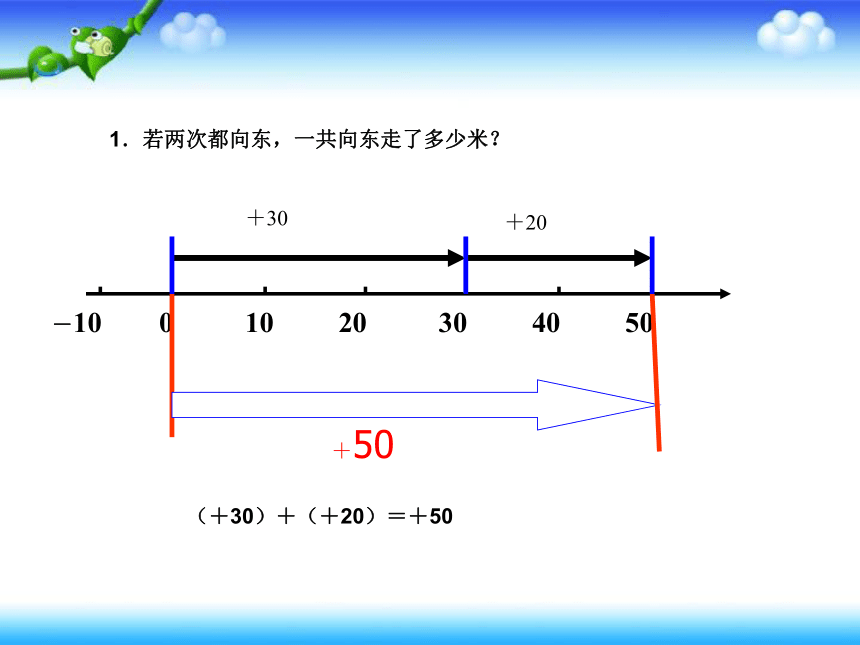
1.若两次都向东,一共向东走了多少米?
(+30)+(+20)=+50
-10 0 10 20 30 40 50
+30
+20
+50
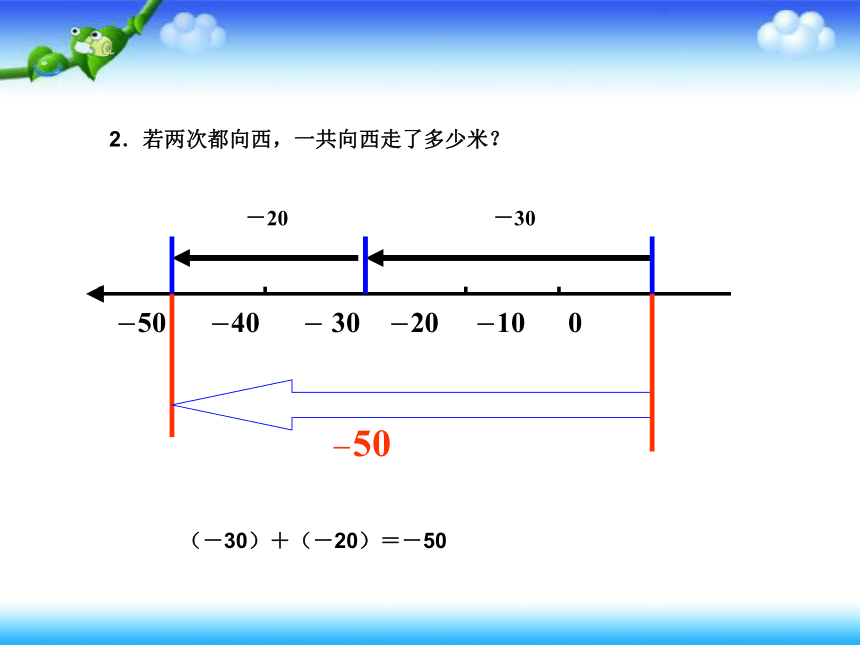
2.若两次都向西,一共向西走了多少米?
(-30)+(-20)=-50
-50 -40 - 30 -20 -10 0
-20
-30
-50
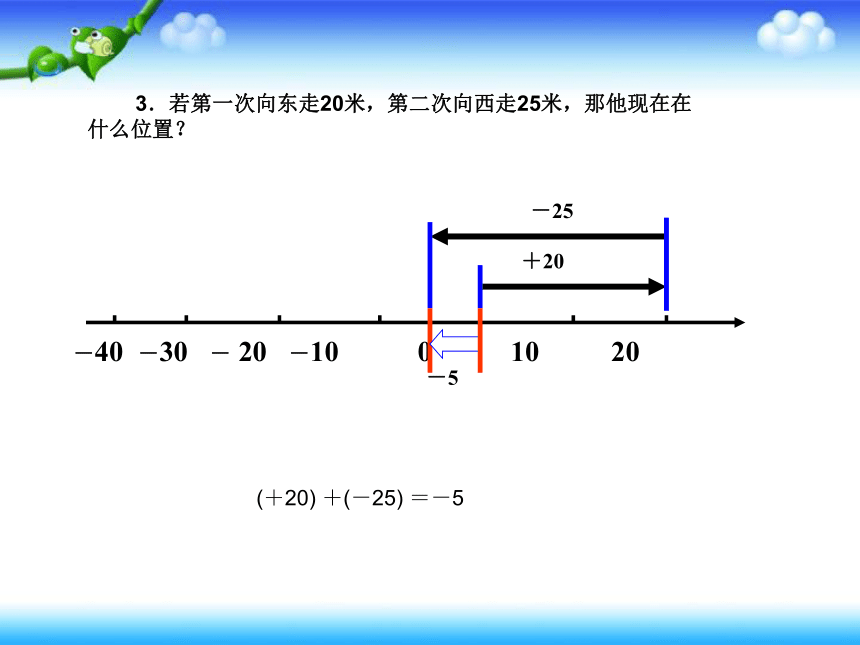
3.若第一次向东走20米,第二次向西走25米,那他现在在什么位置?
(+20) +(-25) =-5
-40 -30 - 20 -10 0 10 20
-25
+20
-5
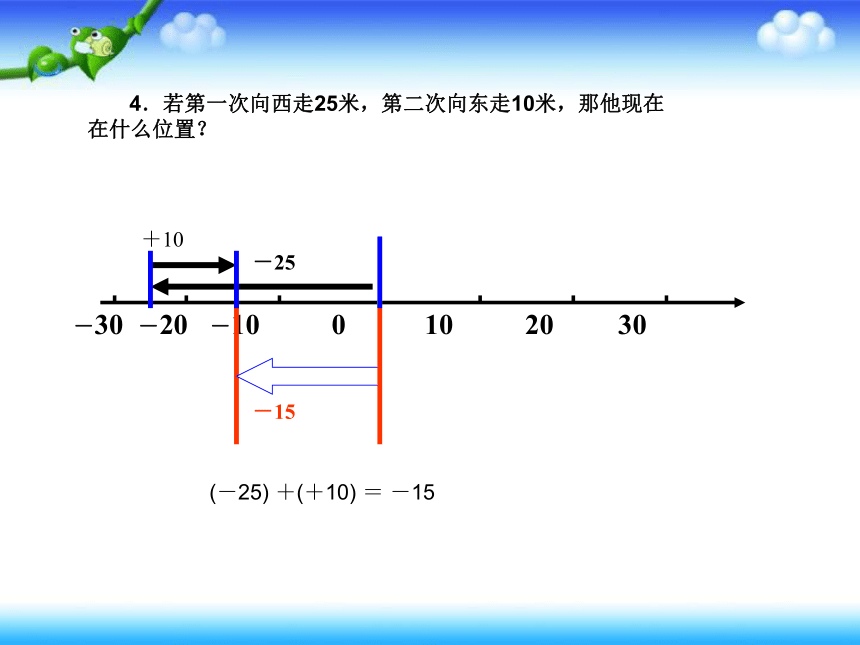
4.若第一次向西走25米,第二次向东走10米,那他现在在什么位置?
(-25) +(+10) = -15
-30 -20 -10 0 10 20 30
-25
+10
-15
5.若第一次向西走20米,第二次向东走20米,那他现在在什么位置?
(-20) +(+20) =0
-50 -40 - 30 -20 -10 0
+20
-20
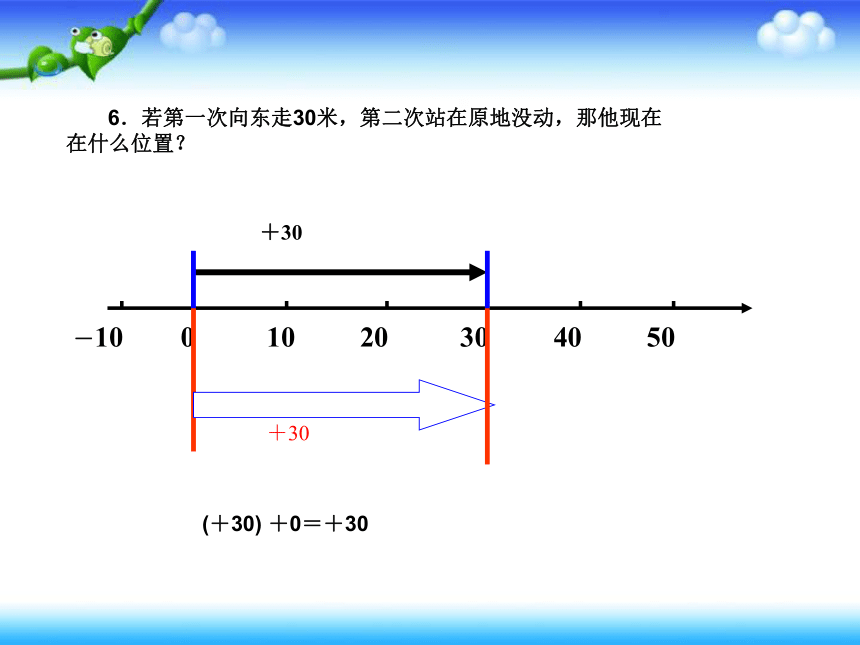
6.若第一次向东走30米,第二次站在原地没动,那他现在在什么位置?
(+30) +0=+30
-10 0 10 20 30 40 50
+30
+30
有理数加法有没有规律?
1.和的符号与两个加数的符号有什么关系?
2.和的绝对值与两个加数的绝对值又有什么关系?
想一想
观察、比较下面几个式子,看能否从这些算式中得到启发,想办法归纳出有理数加法的法则?
(+30)+(+20)=+50
(-30)+(-20)=-50
( 20)+( 25)= 5
( 25)+ ( 10)= 15
( 20)+( 20)=0
(+30)+0=+30
有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
知识要点
例1:计算:
(1)(-4)+(-8);
(2)(-5)+13;
(3)0+(-7);
(4)(-4.7)+3.9.
解:(1)(-4)+(-8)
=-(4+8)
=-12
(2)(-5)+13=+(13-8)=8
(3)0+(-7)=-7
(4)(-4.7)+4.7=-4.7+4.7=0
互为相反意义的量可以全部抵消或部分抵消.
红队 黄队 蓝队 净胜球
红队 4:1 0:1 2
黄队 1:4 1:0 -2
蓝队 1:0 0:1 0
例2:足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数。
三场比赛中,红球共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
篮球共进( )球,失( )球,净胜球数为( ).
1
1
(+1)+(-1)=0
(1)16+(-12)___(-12)+16;
(2)(-19)+(-8)____(-8)+(-19);
(3)(-6.9)+1.5 ___1.5+(-6.9);
(4)0.5+(-5.9)___(-5.9)+0.5.
在横线上填上适当的符号,使两边的式子成立.
=
=
=
=
加法的交换律
有理数的加法中,两个数的加法,交换加数的位置,和不变.
即:a+b=b+a
1.式子中的字母分别表示任意的一个有理数。(如:既可成表示整数,也可以表示分数;既可以表示正数,也可以表示负数或0).
2.在同一个式子中,同一个字母表示同一个数.
知识要点
(1)[16+(-12)] +2_____16+ [(-12)+2]
(2)[(-19)+(-8)] +6____(-19)+ [(-8)+6]
(3)[(-6.9)+1.5] +9____(-6.9) + [1.5+9]
(4)[0.5+(-5.9)] +(-8)_____0.5+ [(-5.9)+(-8)]
=
=
=
=
在横线上填上适当的符号,使两边的式子成立.
加法的结合律
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
即:(a+b)+c =a+(b+c).
知识要点
例3:计算:
(1)24+(-12)+20+(-15);
(2)(-2.54)+3.56+(-7.46)+(-3.56).
解(1)24+(-12)+20+(-15)
=24+20+[(-12)+(-15)]
=44+(-27)
=17
这里使用了哪些运算律 ?
(2)(-2.54)+3.56+(-7.46)+(-3.56)
=[(-2.54)+(-7.46)] +[(+3.56)+
(-3.56)]
=(-10)+0
=-10.
有理的加法常用的三个规律:
1. 一般地,总是先把正数或负数分别结合在一起相加.
2.有相反数的可先把相反数相加,能凑整的可先凑整.
3.有分母相同的,可先把分母相同的数结合相加.
归纳
例4:每袋小麦的标准重量为90千克,10袋小麦称重记录如图所示。与标准重量比较,10袋小麦总计超过多少千克或不足多少千克?10袋小麦的总重量是多少?
解法1:先计算10袋小麦的总重量
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1+91.1=905.4
再计算总计超过多少千克:
905.4-90×10=5.4
解法2:每袋小麦超过标准重量的千克数记作正数,不足的千克数记作负数。
10袋小麦对应的数为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1。
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+(1+1.5+1.8+1.1)
=5.4
90×10+5.4=905.4
答:10袋不麦一共905.4千克,总计超过5.4千克.
数扩展到有理数之后,下面这些结论还成立吗?请说明理由.
(1)若两个数的和是0,则这两个数都是0;
(2)任何两数相加,和不小于任何一个加数.
议一议
1.加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
若a>0,b>0,则a+b=+(|a|+|b|);
若a<0,b<0,则a+b=- (|a|+|b|).
课堂小结
(2)绝对值不相等的异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值;
若a>0,b<0,且|a|>|b|,则a+b=+(|a|-|b|)
若a>0,b<0,且|a|>|b|,则a+b=- (|b|+|a|)
(3)互为相反数的两个数相加得0;
若a>0,b<0,且|a|=|b|,则a+b=0;
a+0=a.
(4)一个数同0相加,仍得这个数.
2.加法运算律
(1)加法交换律:
a+b=b+a;
(2)加法结合律:
(a+b)+c=a+(b+c).
1.如果两个有理数的和为正数,则下列正确的是( )
A.两个数一定都是正数
B.两数都不为零
C.两个数中至少有一个为正数
D.两个数中至少有一个为负数
C
随堂练习
2.计算
解:
3.已知|a|=2,|b|=3,求a+b的值.
解:因为|a|=2,|b|=3,
所以a=±2,b=±3
所以当a=2,b=3时,a+b=2+3=5
当a=2,b=-3时,a+b=2+(-3)=-1
当a=-2,b=3时,a+b=-2+3=1
当a=-2,b=-3时,a+b=-2+(-3)=-5.
解:
5.仓库内原存粮食3500千克,一周内存入和取出情况如下(存入为正,单位:千克):-1500,2000,-800,700,-1000,1200,-240,问第七天末仓库内还存有多少粮食?
解:
3500-1500+2000-800+700-1000+1200-240 =3860
答:第七天末仓库内还存有3860千克粮食.
谢谢欣赏
1.5 有理数的加法
知识与能力
1.经历探索有理数加法法则的过程,理解有理数加法的意义,理解并掌握有理数加法的法则;
2.应用有理数加法法则进行准确运算.
教学目标
过程与方法
1.通过有理数加法的学习,学习化归的意识、数形结合和分类的思想方法,培养观察、比较和概括的思维能力。
2.能够由特殊到一般,总结出有理数的加法法则,培养一定的归纳能力及语言表达能力。
教学目标
情感态度与价值观
体会在总结有理数加法法则的过程中与他人合作、交流的重要性,并且意识到数学与现实生活是紧密相连的.
教学目标
重点
有理数加法法则.
难点
异号两数相加的法则.
教学重难点
小刚在一条东西向的跑道上,先走了30米,又走了20米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
1.若两次都向东,一共向东走了多少米?
(+30)+(+20)=+50
-10 0 10 20 30 40 50
+30
+20
+50
2.若两次都向西,一共向西走了多少米?
(-30)+(-20)=-50
-50 -40 - 30 -20 -10 0
-20
-30
-50
3.若第一次向东走20米,第二次向西走25米,那他现在在什么位置?
(+20) +(-25) =-5
-40 -30 - 20 -10 0 10 20
-25
+20
-5
4.若第一次向西走25米,第二次向东走10米,那他现在在什么位置?
(-25) +(+10) = -15
-30 -20 -10 0 10 20 30
-25
+10
-15
5.若第一次向西走20米,第二次向东走20米,那他现在在什么位置?
(-20) +(+20) =0
-50 -40 - 30 -20 -10 0
+20
-20
6.若第一次向东走30米,第二次站在原地没动,那他现在在什么位置?
(+30) +0=+30
-10 0 10 20 30 40 50
+30
+30
有理数加法有没有规律?
1.和的符号与两个加数的符号有什么关系?
2.和的绝对值与两个加数的绝对值又有什么关系?
想一想
观察、比较下面几个式子,看能否从这些算式中得到启发,想办法归纳出有理数加法的法则?
(+30)+(+20)=+50
(-30)+(-20)=-50
( 20)+( 25)= 5
( 25)+ ( 10)= 15
( 20)+( 20)=0
(+30)+0=+30
有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
知识要点
例1:计算:
(1)(-4)+(-8);
(2)(-5)+13;
(3)0+(-7);
(4)(-4.7)+3.9.
解:(1)(-4)+(-8)
=-(4+8)
=-12
(2)(-5)+13=+(13-8)=8
(3)0+(-7)=-7
(4)(-4.7)+4.7=-4.7+4.7=0
互为相反意义的量可以全部抵消或部分抵消.
红队 黄队 蓝队 净胜球
红队 4:1 0:1 2
黄队 1:4 1:0 -2
蓝队 1:0 0:1 0
例2:足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数。
三场比赛中,红球共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
篮球共进( )球,失( )球,净胜球数为( ).
1
1
(+1)+(-1)=0
(1)16+(-12)___(-12)+16;
(2)(-19)+(-8)____(-8)+(-19);
(3)(-6.9)+1.5 ___1.5+(-6.9);
(4)0.5+(-5.9)___(-5.9)+0.5.
在横线上填上适当的符号,使两边的式子成立.
=
=
=
=
加法的交换律
有理数的加法中,两个数的加法,交换加数的位置,和不变.
即:a+b=b+a
1.式子中的字母分别表示任意的一个有理数。(如:既可成表示整数,也可以表示分数;既可以表示正数,也可以表示负数或0).
2.在同一个式子中,同一个字母表示同一个数.
知识要点
(1)[16+(-12)] +2_____16+ [(-12)+2]
(2)[(-19)+(-8)] +6____(-19)+ [(-8)+6]
(3)[(-6.9)+1.5] +9____(-6.9) + [1.5+9]
(4)[0.5+(-5.9)] +(-8)_____0.5+ [(-5.9)+(-8)]
=
=
=
=
在横线上填上适当的符号,使两边的式子成立.
加法的结合律
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
即:(a+b)+c =a+(b+c).
知识要点
例3:计算:
(1)24+(-12)+20+(-15);
(2)(-2.54)+3.56+(-7.46)+(-3.56).
解(1)24+(-12)+20+(-15)
=24+20+[(-12)+(-15)]
=44+(-27)
=17
这里使用了哪些运算律 ?
(2)(-2.54)+3.56+(-7.46)+(-3.56)
=[(-2.54)+(-7.46)] +[(+3.56)+
(-3.56)]
=(-10)+0
=-10.
有理的加法常用的三个规律:
1. 一般地,总是先把正数或负数分别结合在一起相加.
2.有相反数的可先把相反数相加,能凑整的可先凑整.
3.有分母相同的,可先把分母相同的数结合相加.
归纳
例4:每袋小麦的标准重量为90千克,10袋小麦称重记录如图所示。与标准重量比较,10袋小麦总计超过多少千克或不足多少千克?10袋小麦的总重量是多少?
解法1:先计算10袋小麦的总重量
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1+91.1=905.4
再计算总计超过多少千克:
905.4-90×10=5.4
解法2:每袋小麦超过标准重量的千克数记作正数,不足的千克数记作负数。
10袋小麦对应的数为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1。
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+(1+1.5+1.8+1.1)
=5.4
90×10+5.4=905.4
答:10袋不麦一共905.4千克,总计超过5.4千克.
数扩展到有理数之后,下面这些结论还成立吗?请说明理由.
(1)若两个数的和是0,则这两个数都是0;
(2)任何两数相加,和不小于任何一个加数.
议一议
1.加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
若a>0,b>0,则a+b=+(|a|+|b|);
若a<0,b<0,则a+b=- (|a|+|b|).
课堂小结
(2)绝对值不相等的异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值;
若a>0,b<0,且|a|>|b|,则a+b=+(|a|-|b|)
若a>0,b<0,且|a|>|b|,则a+b=- (|b|+|a|)
(3)互为相反数的两个数相加得0;
若a>0,b<0,且|a|=|b|,则a+b=0;
a+0=a.
(4)一个数同0相加,仍得这个数.
2.加法运算律
(1)加法交换律:
a+b=b+a;
(2)加法结合律:
(a+b)+c=a+(b+c).
1.如果两个有理数的和为正数,则下列正确的是( )
A.两个数一定都是正数
B.两数都不为零
C.两个数中至少有一个为正数
D.两个数中至少有一个为负数
C
随堂练习
2.计算
解:
3.已知|a|=2,|b|=3,求a+b的值.
解:因为|a|=2,|b|=3,
所以a=±2,b=±3
所以当a=2,b=3时,a+b=2+3=5
当a=2,b=-3时,a+b=2+(-3)=-1
当a=-2,b=3时,a+b=-2+3=1
当a=-2,b=-3时,a+b=-2+(-3)=-5.
解:
5.仓库内原存粮食3500千克,一周内存入和取出情况如下(存入为正,单位:千克):-1500,2000,-800,700,-1000,1200,-240,问第七天末仓库内还存有多少粮食?
解:
3500-1500+2000-800+700-1000+1200-240 =3860
答:第七天末仓库内还存有3860千克粮食.
谢谢欣赏
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
